Конспект лекций по курсу «финансовый менеджмент»

Вид материала

Конспект

Содержание 6.4. Бессрочная рента Бессрочная рента: поток равнозначных выплат, которые предусматривается без определения срока выплат (вечно РV (бессрочная рента)=$10 РV (бессрочная рента)=$10 Вопросы для самопроверки 6. 5. Несколько упрощенных способов вывода формул расчета денежных потоков Бессрочная рента (консоль) Ежегодная рента Рост ежегодной ренты 7.1. Текущая стоимость неравномерных денежных потоков 7.2. Будущая стоимость неравномерных денежных потоков Вопросы для самопроверки 8. Амортизационные кредиты Амортизационный график 9. Сколько стоит фирма Текущая стоимость фирмы Фактор текущей стоимости (10%) Непрерывное компаундирование

Подобный материал:

• Курс лекций тема Предмет и задачи курса «Финансовый менеджмент» Учебная дисциплина, 2104.19kb.
• Конспект лекций из|с| дисциплины "Компьютерные сети и телекоммуникации" для специальности, 674.68kb.
• Конспект лекций по курсу «Организация производства», 2032.47kb.
• Конспект лекций по курсу «Организация производства», 2034.84kb.
• Конспект лекций по курсу «Международный менеджмент», 391.99kb.
• Конспект лекций по курсу "Начертательная геометрия и инженерная графика" Кемерово 2002, 786.75kb.
• Конспект лекций по курсу: «основы менеджмента», 925.89kb.
• Конспект лекций по дисциплине «Стратегическое управление», 960.8kb.
• Конспект лекций по курсу «бизнес-планирование в условиях рынка», 461.46kb.
• Конспект лекций для студентов специальности «Менеджмент организации», 858.96kb.

6.4. Бессрочная рента

Бессрочная рента: поток равнозначных выплат, которые предусматривается без определения срока выплат (вечно).

Большинство рент рассчитаны на определенное количество выплат, которые осуществляются за определенное количество лет - например, 100 долларов США в год в течение трех лет. Однако существуют ренты, сроки которых не определяются. Такие ренты называются бессрочными. Текущая стоимость такого рода рент может быть рассчитана при помощи уравнения

PV (бессрочная рента) = выплаты / процентная ставка = PMT / i

Характер пожизненной ренты может быть ясно проиллюстрирован британскими ценными бумагами, выпущенными в период после войны с Наполеоном. В 1815 году британское правительство продало большое количество облигаций и использовало полученные от продажи средства для выплат по многим мелким выпускам ценных бумаг, выпущенным еще в довоенный период. Вследствие того, что целью выпуска облигаций было консолидирование прошедших долгов, облигации получили наименование консолей.

Консоль:

пожизненная облигация, выпущенная британским правительством для консолидирования прошедших долгов, фактически, так называются любые пожизненные облигации.


Припустим, по каждой такой облигации было обещано бессрочно платить по $100 в год (на самом деле выплаты осуществлялись в фунтах стерлингов). Сколько должна была стоить каждая облигация, если дисконтная ставка была 5%?

Ответ - $2000. РV (бессрочная рента)=$100 / 0,05= $2000 при i=5%.


Припустим, процентная ставка поднимается до 10 процентов: что произойдет со стоимостью консолей?

Их стоимость упадет к $1000:

РV (бессрочная рента)=$100 / 0,10= $1000 при i=10%.

Следовательно, мы видим, что стоимость пожизненной ренты в значительной мере зависит от величины процентной ставки. Проблемы бессрочных рент будут рассматриваться нами в следующем разделе, в котором также будут описаны варианты определения стоимости различных типов ценных бумаг.

Вопросы для самопроверки

Что происходит со стоимостью пожизненных рент, если процентная ставка растет?

Что происходит, если процентная ставка уменьшается?

Почему происходят " эти изменения?


6. 5. Несколько упрощенных способов вывода формул расчета денежных потоков

Эта секция вводит несколько упрощений оценки денежных потоков. Развитие этих коротких вставок иллюстрирует несколько 'хитростей' оценки, которые полезны в решении проблем NPV. Использование линии времени денежных потоков полезно для каждого из примеров.

Бессрочная рента (консоль)

ПРИМЕР $100 каждый период времени выплачиваются в течение неограниченного периода. Процентная ставка равна 10% за период




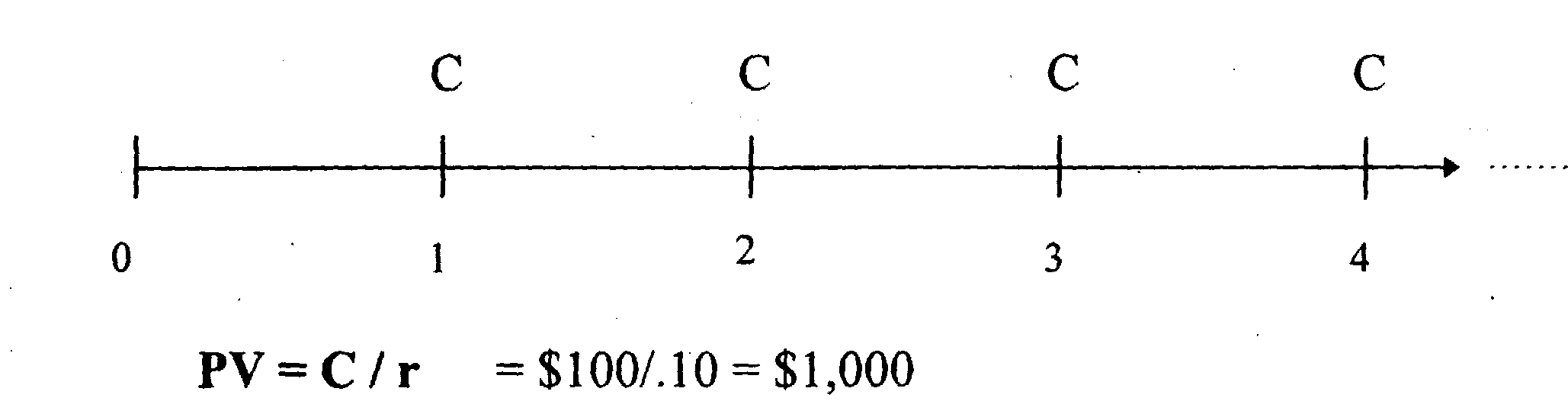
Эта формула делает интуитивное чувство, что каждый период купонная оплата (процент), равна C = PV*r (например $1,000 *. 1 = $100) может быть оплачен без использования PV основной суммы.


Возрастающая бессрочная рента

ПРИМЕР $100 полученные в 1 периоде, возрастают на 2% за каждый последующий период в течении неограниченного времени. Процентная ставка равна 10% за период





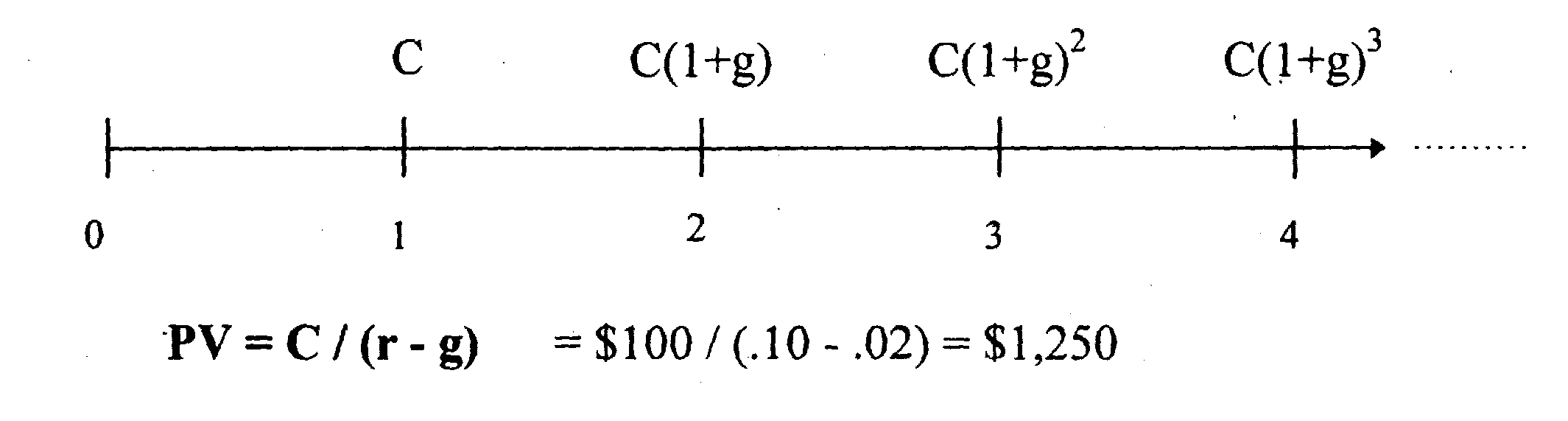
Ежегодная рента


ПРИМЕР $50,000 за период выплачиваются на протяжении 20 периодов. Процентная ставка равна 10% за период




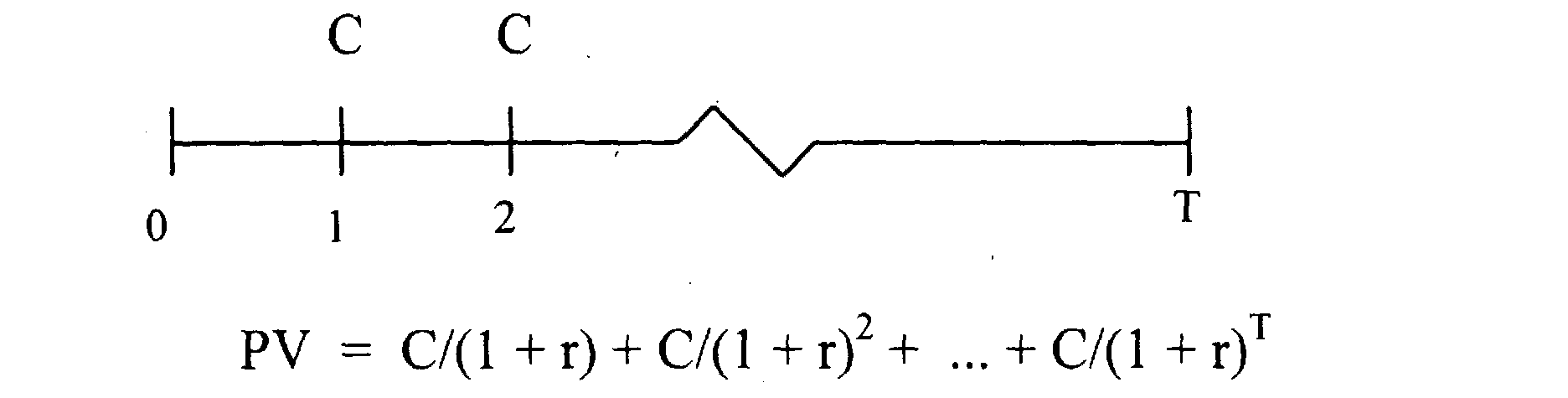
Эти денежные потоки равноценны




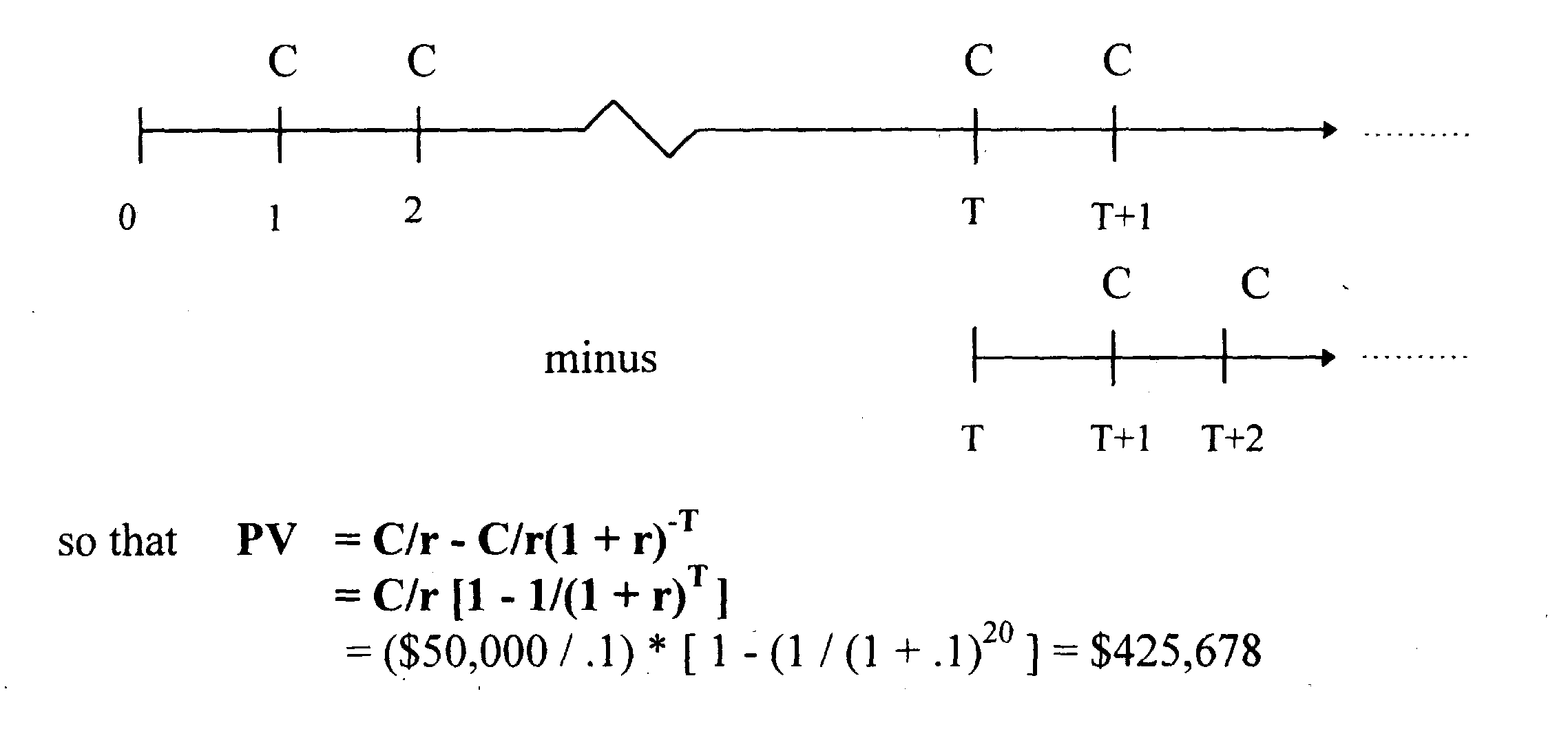
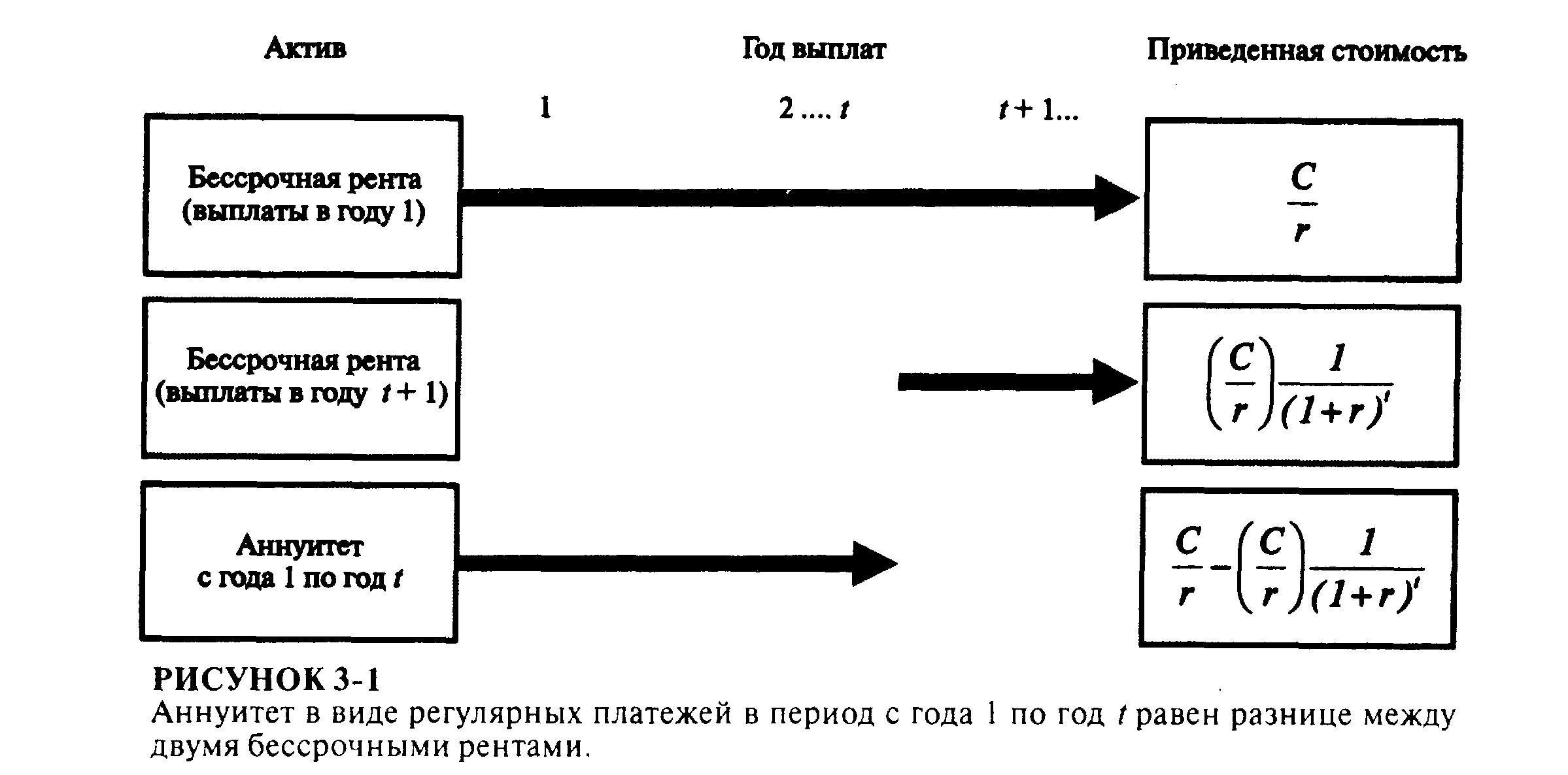
Или то же выраженное другим способом


Более строгий вывод можно представить следующим образом






Рост ежегодной ренты

$50,000 полученные в 1 периоде, возрастают на 2% за каждый последующий период на протяжении 20 периодов. Процентная ставка равна 10% за период




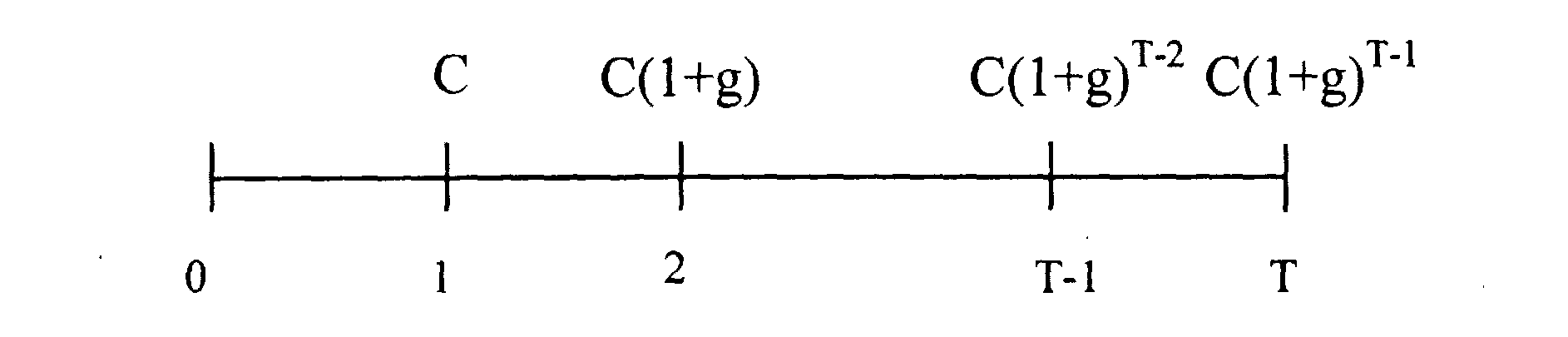
Эти денежные потоки равноценны





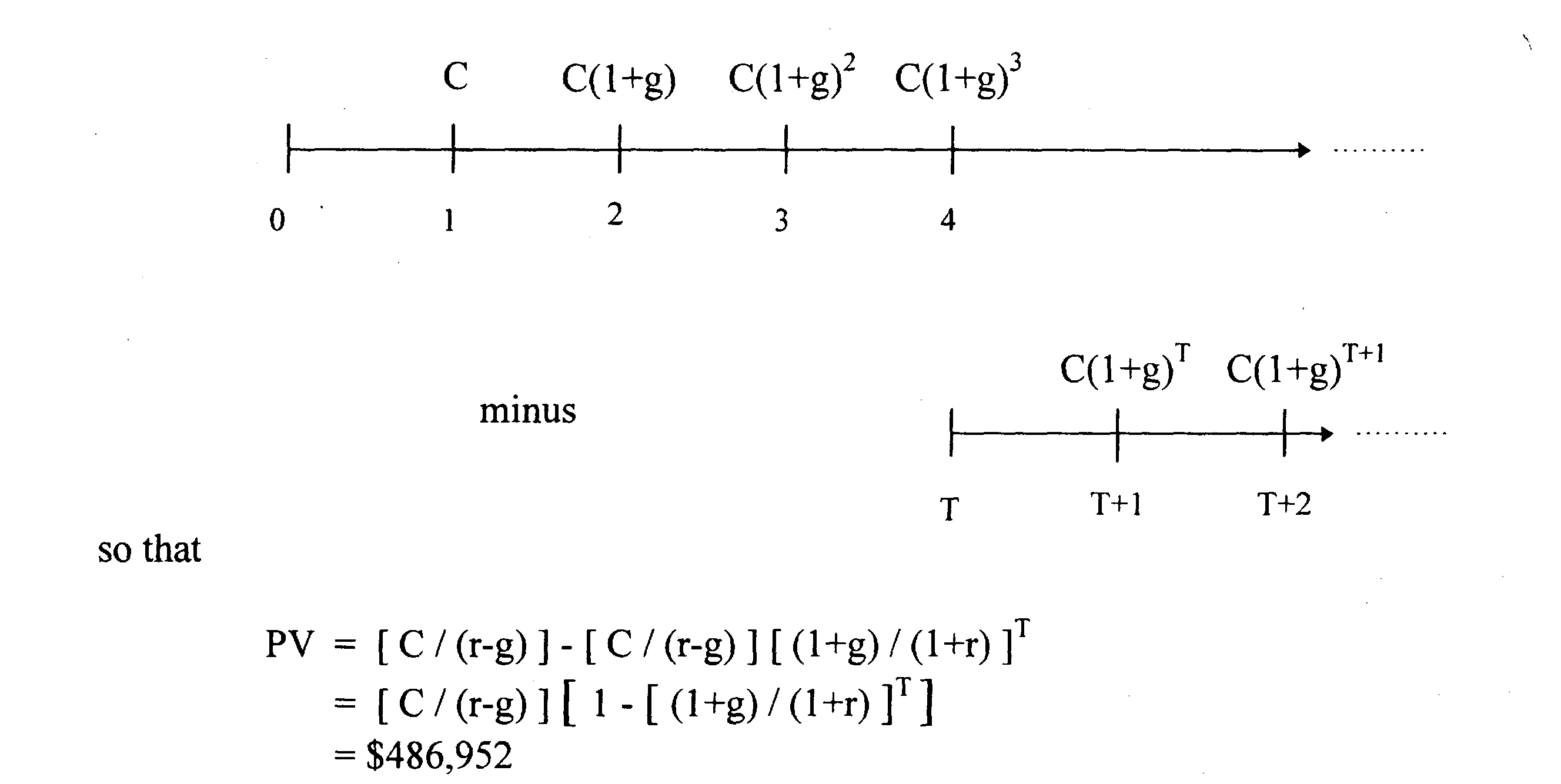
• 7. Неравномерное движение потока наличности

Определение ренты обязательно включает слова: "равнозначные суммы". Иными словами, рента базируется на равнозначных выплатах, которые осуществляются через равные периоды времени. Но хотя большинство финансовых решений действительно базируются на такого рода выплатах, некоторые из них допускают неравномерные выплаты. Например, по обычным акциям выплаты дивидендов, конечно, имеют характер нарастания, выплаты по инвестициям в фиксированные активы (например, в новое оборудование) также не допускают равномерных денжных потоков. Таким образом, для дальнейшего обсуждения проблемы временной стоимости нам следует обдумать понятие неравномерных движений денежных потоков.


Неравномерное движение потоков наличности: серия потоков наличности, суммы которых меняются от периода к периоду.

Выплаты (РМТ): срок, который определяет равные потоки наличности в равные периоды времени.

Поток наличности: срок, который значит неравномерные потоки наличности.


В течение этой лекции и далее мы будем строго придерживаться условия и пользоваться термином "выплата" (РМТ) для ситуаций, которые описывают ренту, и термином "денежный поток", "поток наличности" (СF) для определения неравномерных потоков наличности. Построение финансовых калькуляторов также отвечает этим правилам.

7.1. Текущая стоимость неравномерных денежных потоков

Текущая стоимость неравномерных денежных потоков определяется как сумма текущих стоимостей отдельных денежных потоков. Например, припустим, что мы должны вычислить текущую стоимость следующего потока наличности при дисконтной ставке в 6 процентов:




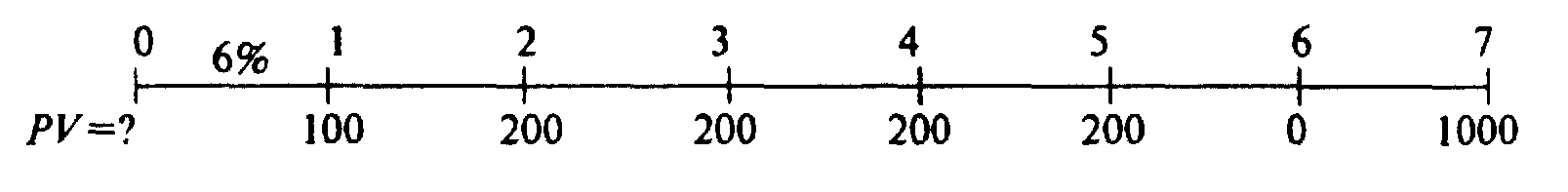
Текущая стоимость может быть рассчитана при помощи общего уравнения текущей стоимости:





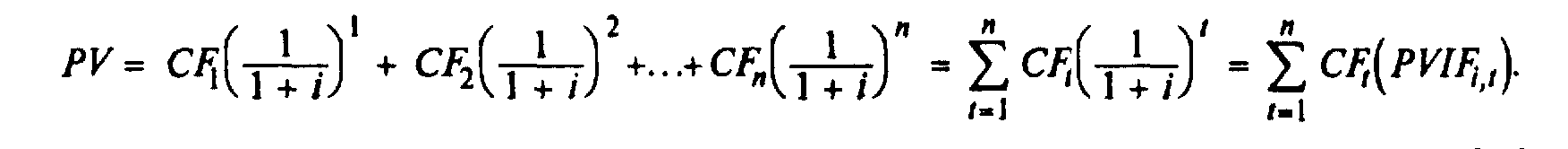
Кроме того, для определения текущей стоимости потока наличности можно обратиться к такому методу: найти при помощи числового метода, финансового калькулятора или таблицы значения отдельных потоков наличности, а потом просуммировать их. Такой процесс будет выглядеть таким образом:



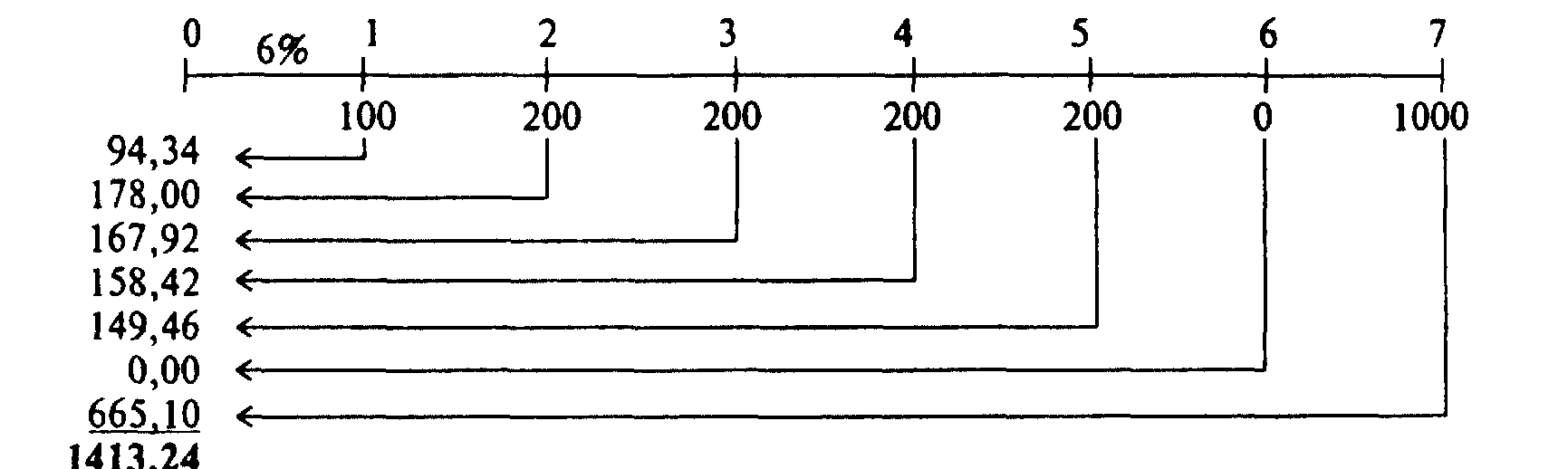
Мы должны были сделать следующее: воспользоваться уравнением, указать текущие стоимости отдельных потоков наличности в левом столбике диаграммы и потом просуммировать их. В результате мы получили текущую стоимость всего потока наличности.

Общая текущая стоимость потоков наличности может быть высчитана при помощи подытоживания текущих стоимостей отдельных потоков наличности, как это показано выше. Однако этот процесс может быть немного сокращен благодаря определенной регулярности всего потока. Отметьте, например, что потоки наличности 2, 3, 4 и 5 показывают сумму ренты. Мы можем воспользоваться этим фактом для того, чтобы решить задачу немного другим способом:





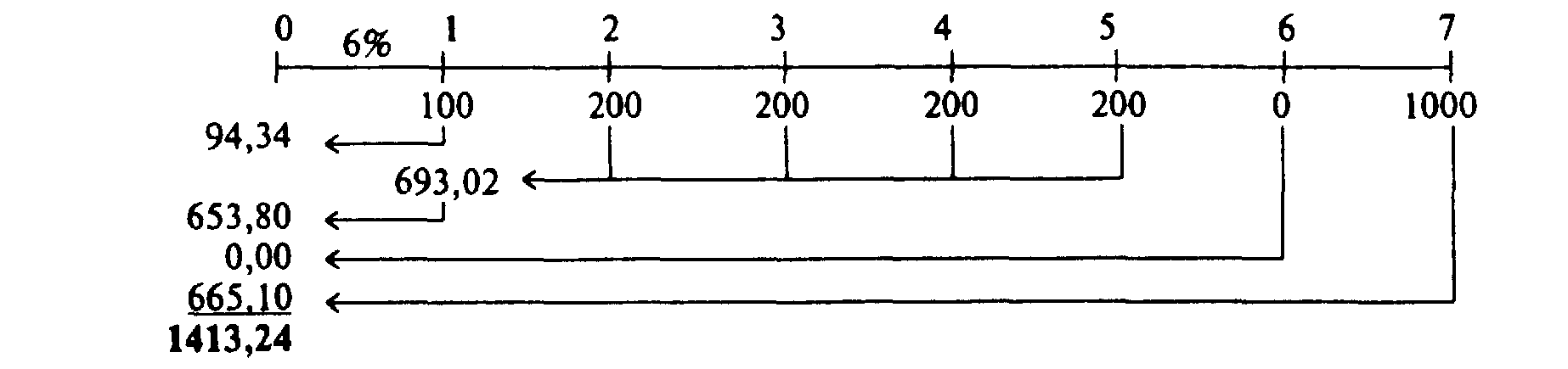
Потоки наличности с 2 по 5 период показывают обычную, или отсроченную ренту. Мы находим текущую стоимость этой ренты за год 1 (за один период к первой выплате). После этого данный показатель (693,02 доллара США) дисконтируется на один период назад, в результате чего мы имеем стоимость года 0, т.е. 653,80.


Вычисление PV неравномерных денежных потоков при помощи финансового калькулятора.

Задачи, которые касаются неравномерных потоков наличности, могут быть решены с помощью большинства финансовых калькуляторов одним мероприятием. В первую очередь, Вам необходимо ввести показатели отдельных потоков наличности в хронологическом порядке в регистр потока наличности. Конечно, эти показатели отражаются СF0, СF1, СF2, СF , и т. д. Потом Вы вводите показатель процентной ставки. После этого Вам остается только нажать кнопку NPV, в результате чего получите текущую стоимость всего потока. Большинство калькуляторов запрограммировано на автоматическое определение текущих стоимостей отдельных потоков наличности и их суммирование. Чтобы ввести показатели потоков наличности для приведенной нами задачи, следует ввести по порядку 0 (потому, что СF0 =0), 100, 200, 200, 200, 200, 0, 1000 в регистр потока наличности, потом ввести i=6 и нажать кнопку NPV для получения ответа, который в данном случае будет 1413,19. Этот ответ немного отличается от ответов, полученных другими методами, что происходит в результате закругления в процессе расчетов.

Здесь следует обратить особое внимание на два момента. Во-первых, при использовании регистру потока наличности помните, что в калькуляторах вместо термина РV используется термин. NPV. N - "нетто", что в переводе значит - чистый, так что NРV значит "чистая текущая стоимость".

7.2. Будущая стоимость неравномерных денежных потоков

Конечная стоимость: будущая общая стоимость неравномерных потоков наличности.

Будущая стоимость неравномерных потоков наличности (иногда ее еще называют конечной стоимостью) определяется с помощью компаундирования каждой выплаты в конце периода вплоть до прекращения выплат, и потом суммированием будущих стоимостей:







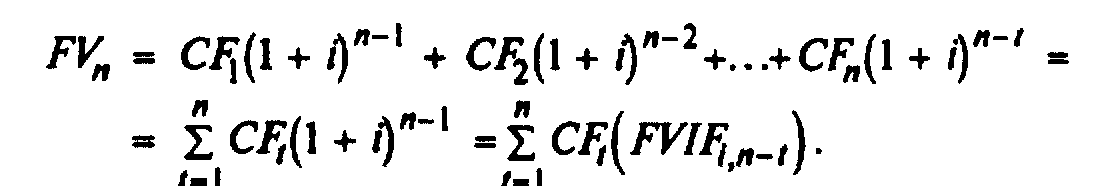
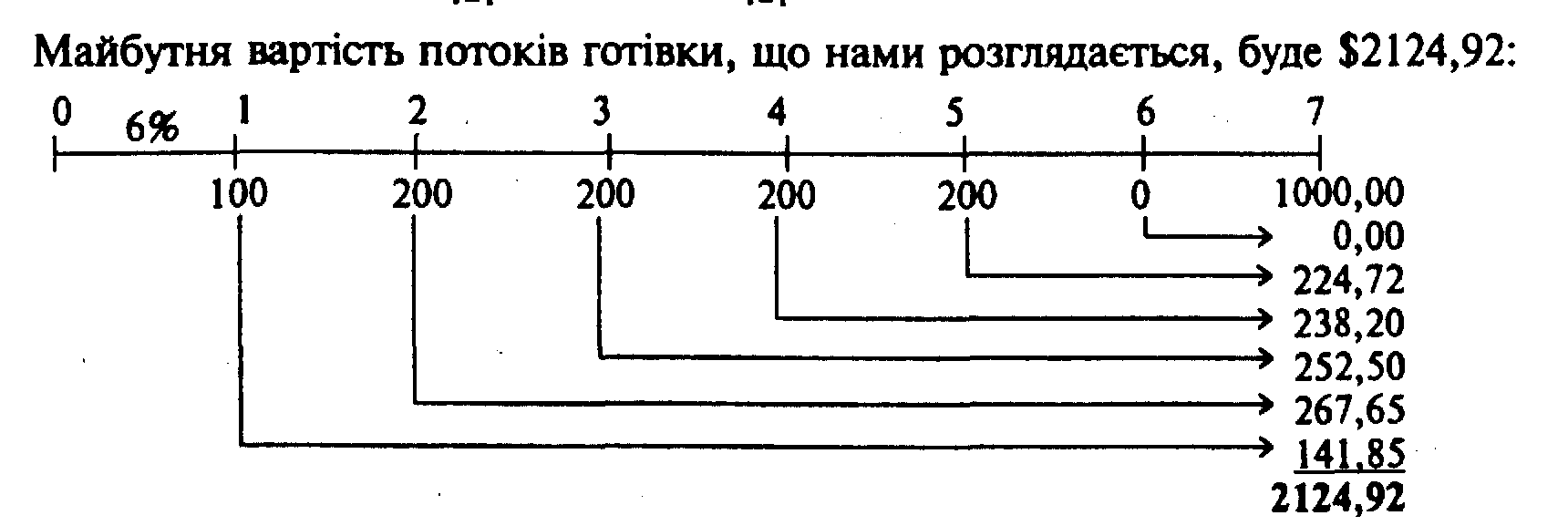
В некоторых финансовых калькуляторах есть кнопка "NFV" (чистая будущая стоимость). После того, как Вы ввели показатели наличности и процентной ставки в память калькулятора. Вы можете при помощи этой кнопки получить значение будущей стоимости всего потока.

Встречаются также калькуляторы, при работе с которыми Вам следует рассчитать текущую стоимость всего потока, а потом определить на ее основе будущую стоимость, компаундированную для n-го числа периодов и i-го показателя процентов. Для примера, что нами рассматривается, следует, пользуясь регистром потоков наличности и известным показателем I = 6. Вычислить показатель FV (в нашем случае = 1413,19). Потом вводим: N=7, I=6, PV= -1413,19, РМТ=0 и нажимаем кнопку FV. В результате получаем сумму FV = 2124,92.


7.3. Определение "і" неравномерных потоков наличности

Довольно легко определить і одноразовых выплат или рент при помощи числового метода или таблиц. Но вычислять і для неравномерных потоков наличности очень тяжело, для этого следует делать сложные и трудоемкие расчеты, которые нуждаются в значительном объеме времени. Однако, это просто делается при помощи финансового калькулятора: для этого Вы должны ввести стоимости потоков наличности в соответствующий регистр и потом нажать кнопку ІRR. Данная аббревиатура значит "internal rаtе", или "внутренняя ставка доходности". Сейчас мы удержимся от обсуждения характера этих расчетов, но в будущем, Вы узнаете об этом подробно.

Для получения результатов при помощи кнопки ІRR необходимо, чтобы когда-нибудь один поток наличности имел знак "минус", который указывает на то, которое это сумма инвестирования. Потому, что в нашем примере все потоки наличности имеют знак "плюс", решение с ІRR невозможно. Однако, если мы введем показатель СF0, например, -1000 долларов США, мы сможем получить ІRR, которая будет отображать ставку прибыли, полученной по данному инвестированию в $1000. В нашем примере это 13,96%.,


Вопросы для самопроверки

Наведите два типичных примеры финансовых решений, связанных с проблемой неравномерных потоков наличности.

Что значит срок "остаточная стоимость"?


• 8. Амортизационные кредиты

Амортизационный кредит: кредит, который платится частями, равномерными взносами

Одной из важных сфер применения компаундированного процента есть кредиты, которые платятся частями, равномерными взносами. К таким кредитам относятся автомобильные, студенческие кредиты, кредиты по залогу недвижимости, много других кратковременных кредитов и долгосрочных облигаций. Если кредит должен платиться частями и равномерными взносами, то такой кредит называется амортизационным.

Для иллюстрации вышесказанного припустим, что фирма взяла кредит на $1000 с обязательством выплачивать его тремя равными частями в конце каждого года в течение трех следующих лет. (В таком случае должно выполняться по одной выплате на год, поэтому количество лет равно количеству периодов, а номинальная процентная ставка равна периодической ставке). Заимодатель должен получать шесть процентов по заимообразному балансу, невыплаченному на начало каждого года. Во-первых, необходимо определить, какую сумму фирма должна платить каждый год, т.е., сумму ежегодных выплат. Для этого мы будем выходить из того, что сумма в $1000 является текущей стоимостью ренты для ежегодной выплаты у РМТ долларов США в течение 3 лет при 6-процентном дисконтировании.


Часовая линия и уравнение:





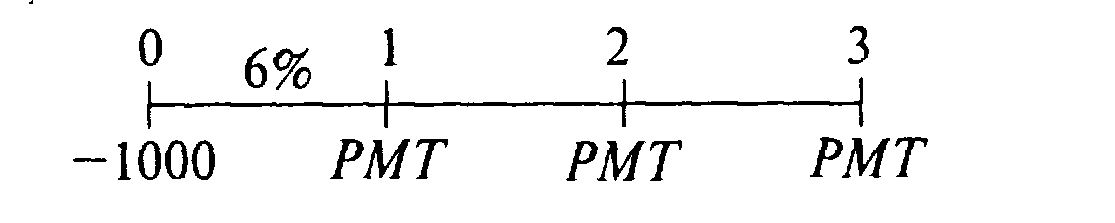
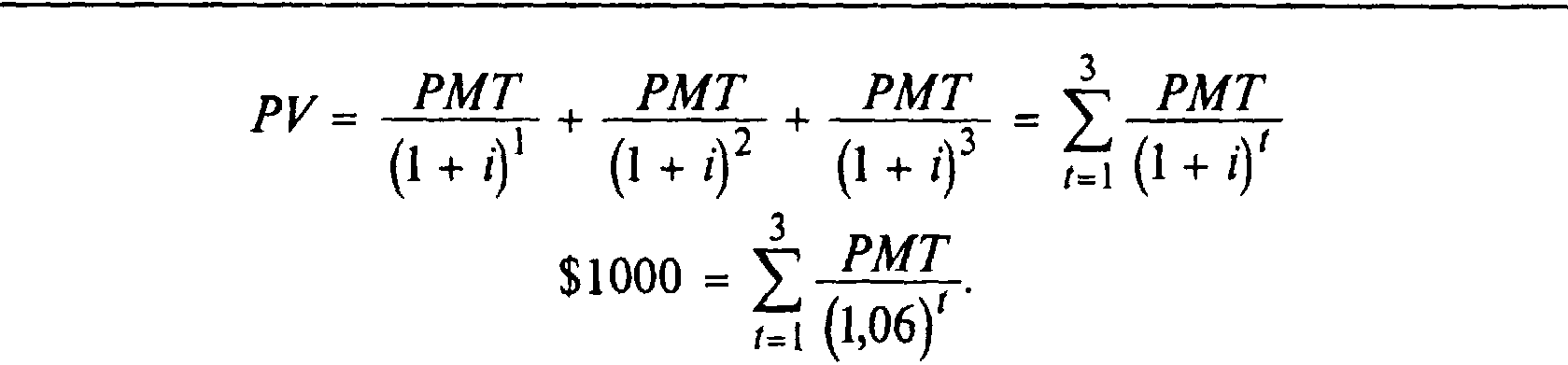
В данном равнении нам известны все переменные, кроме РМТ, поэтому мы легко можем рассчитать эту величину.

1. Числовое решение:

Вы можете обратиться к методу "проб и ошибок", подставляя различные значения РМТ в уравнение до того времени, пока не найдете значения, при котором правая часть уравнения равнялась бы левой, т.е., 1000 дол. США. Это очень длительный и трудоемкий процесс, но, наконец, Вы подберете верное число. И число это будет: РМТ= $374,11.

2. Решение при помощи таблиц:

Подставьте известные значения и найдите в таблице А-2 значение PVIFA для 6% и 3 периодов:



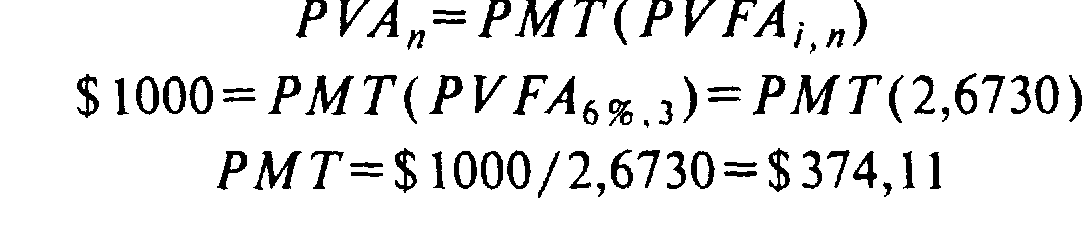
3. Решение при помощи финансового калькулятора:

Вводим данные: Результат:

N 3, I 6, РV 1000, FV 0, РМТ =-347,11


Таким образом, мы узнали, что фирма в течение 3 лет должна будет платить заимодателю $374,11 в конце каждого года при процентной ставке 6%.

Каждая выплата будет состоять из процентов по кредиту и частично - с выплат по основной сумме. Это распределение демонстрируется в амортизационной таблице 6-2. Сумма процента наибольшая для первого года, далее она уменьшается в меру того, как сокращается сумма неуплаченного остатка. С целью определения налоговых расчетов должник-бизнесмен обязан ежегодно сообщать об этом проценте (указанном в столбике 3) как об удержанной с него сумме; заимодатель же дает ту же информацию как показатель своей прибыли.

Финансовые калькуляторы запрограммированы для расчета амортизационных таблиц. Для этого Вам просто следует ввести известные данные, а потом нажиманием кнопки ввести их в таблицу 6-2. Если у Вас есть финансовый калькулятор, Вам следует внимательно прочитать соответствующую часть пособия по пользованию им, где должно быть точно указано, как пользоваться этой функцией калькулятора.


Амортизационный график:

т
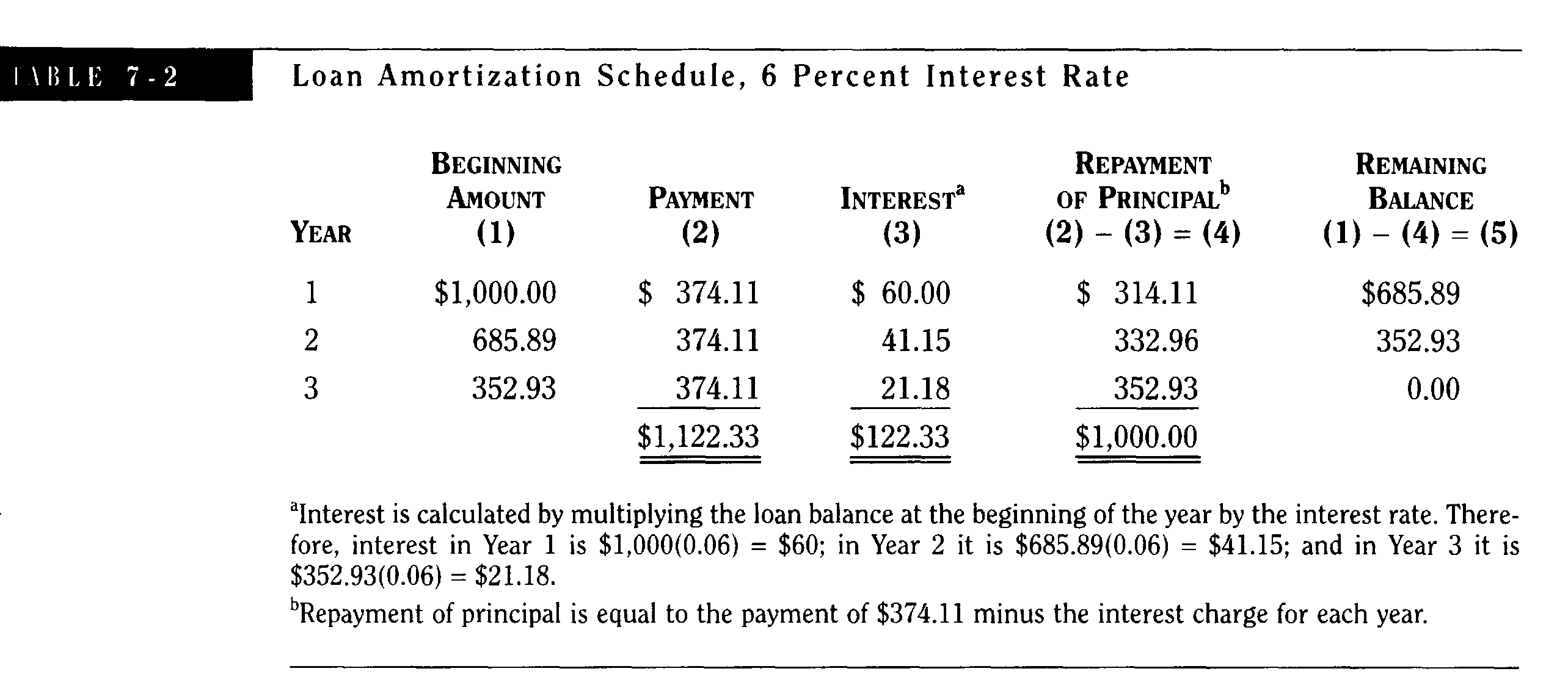
аблица, которая указывает точно, как должны проводиться выплаты. Она содержит данные о том, какие точно суммы должны платиться в определенные даты, а также дает информацию, какая часть будет платиться по процентам, а какая - по основной сумме.


а) Процент рассчитывается путем умножения суммы остатка на начало года на процентную ставку. Таким образом, процент в нашем примере для года 1 будет: $1000 (0,06)=$60;

для года 2: 685,89(006)=$41,15;

для года 3: $352,93(006)=$ 21,18.

б) Выплаты по основным суммам рассчитываются путем вычитания из общей суммы выплат (в нашем примере $374,11) суммы ежегодно выплачиваемого процента.


9. Сколько стоит фирма?

Предположим, что вы занимаетесь определением стоимости малых фирм. (Вы деловой оценщик.) Как можете вы определить то, какую стоимость имеет фирма? Урок, который вы получите из этого примера, есть то, что текущая стоимость фирмы зависит от будущих денежных потоков.

Давайте рассматривать пример фирмы, которая, как полагают, генерирует чистые оплаты (притоки капитала минус прямые платежи) наличными $5,000 в первый год и $2,000 для каждого из следующих пяти лет. Фирма может быть продана за $10,000 через семь лет от данного момента. Владельцы фирмы хотели бы заработать 10 процентов на их инвестиции в фирму.

Стоимость фирмы находится с помощью умножения чистых денежных потоков на соответствующие факторы текущей стоимости. Стоимость фирмы есть просто сумма текущих стоимостей индивидуальных чистых денежных потоков.

Текущая стоимость чистых денежных потоков дана ниже:

Текущая стоимость фирмы

Конец года	Чистый денежный поток фирмы	Фактор текущей стоимости (10%)	Текущая стоимость чистых денежных потоков
1	$ 5,000	.90909	$ 4,545.45
2	2,000	.82645	1,652.90
3	2,000	.75131	1,502.62
4	2,000	.68301	1,366.02
5	2,000	.62092	1,241.84
6	2,000	.56447	1,128.94
7	10,000	.51315	5,131.58
		Текущая стоимость фирмы	$16,569.35

Мы можем также использовать формулу упрощения для ежегодной ренты, чтобы сделать расчет


$5.000 / 1.1 + (2,000 *A5, 0.10) / 1.1 + 10,000 / (1.1)⁷ = $16,569.35


Предположим, что вы имеете возможность приобрести фирму за $12,000. Должны ли вы приобрести фирму? Ответ: да, из-за того, что NPV положителен.

NPV = PV - Стоимость

$4.569.35 = $16,569.35 - $12,000

Дополнительная (превышающая) стоимость (NPV) приобретения фирмы есть $4,569.35.


• пример

Trojan Pizza Company обдумывает инвестирование $1 миллиона в четыре новые проекта в Los Angeles. Andrew Lo, Chief Financial Officer (CFO) фирмы, оценил, что инвестиции принесут оплаты наличными $200,000 в год в течении 9 лет и нет оплаты наличными после 9 года. Mr. Lo определил, что уместный учетный процент для этой инвестиции есть 15 процентов. Это есть коэффициент окупаемости, которую фирма может заработать в сравнимых проектах. Должна ли Trojan Pizza Company сделать инвестиции в новые проекты?

Решение может быть оценено, как:


NPV = -$1,000,000 + 200,000 * A9 0.15

= -$45,683.22


Trojan Pizza Company не должен делать инвестицию, из-за того, что NPV есть - $45,683.22. Если Trojan Pizza Company требует 15 процентов коэффициент окупаемости, новые проекты не есть хорошая инвестиция.

,


Дополнительные Проблемы

Проблема 3.1. Чистая текущая стоимость при различных периодах компаундирования

Общая формула для вычисления, которой задано NPV



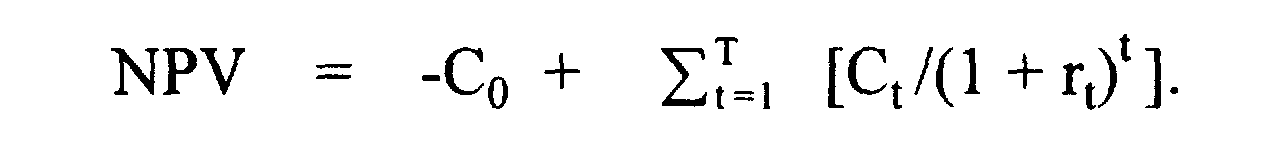
Начальный денежный поток есть обычно инвестиция и так устанавливается, что он должен быть негативным. Суммирование чисел в правой части уравнения вычисляет текущую стоимость всех последующих денежных потоков.

Во многих случаях, r1 = r2 =... = r1i =. .., таким образом, общая формула может быть приведена к виду



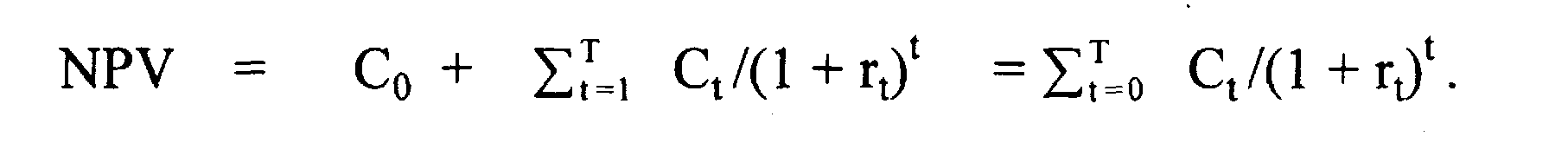
Пример Как пример, предположим, мы пытаемся определить чистую текущую стоимость серии денежных потоков

- Co = -$1000, C1 = $500 и C2 = $700. NPV этих денежных потоков, при процентной ставке r = 9% является:

NPV = -Co + C1 /(l + r1) + C2/(1 + r2) ²


= -$1000 + $500/(1.09)+$700/(1.09) ²

=$47.89.

Периоды компаундирования

Мы даем примеры ежегодного, полугодового и непрерывного компаундирования.


Ежегодное компаундирование

Предположим, что, если вы инвестируете $1000 сегодня, вы ожидаете получить $500 в конце первого года и $700 в конце второго года. Ваша процентная ставка для этого типа инвестиции есть 9% в год начисляемых раз в год. Временная линия денежных потоков будет похожей на:




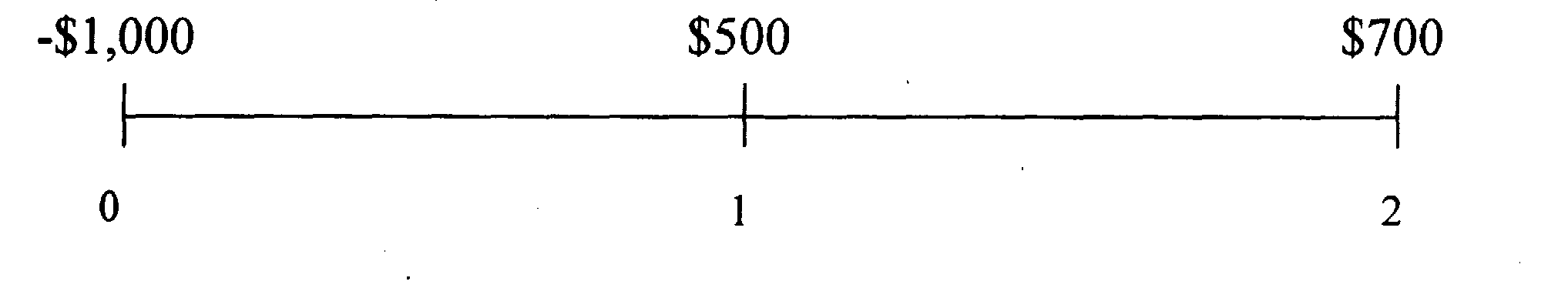
При процентной ставке r = 9%, чистая текущая стоимость инвестиции равна

NPV = -$1000 + $500/1.09 + $700/(1.09) ² = $47.89

Полугодовое компаундирование

Предположим, что ежегодные оплаты в вышеупомянутом примере дисконтируются по ставке 9% годовых, начисляемых раз в полгода.




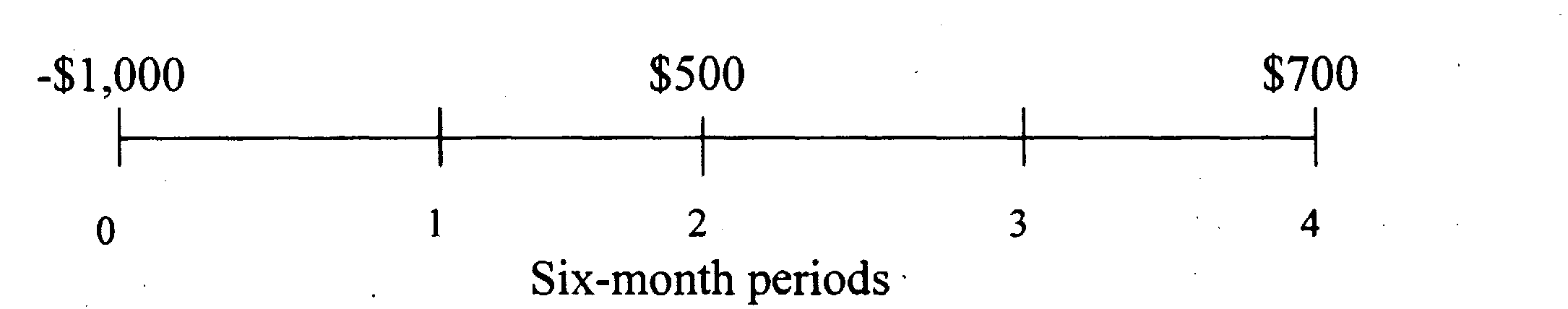
9% годовая ставка в данном примере эквивалентна ставке 4.5% дважды на год. В таком случае,


NPV = -$1000 + $500/(1.045) ² + $700/(1.045) ⁴ = $45.12


9% есть установленная (или номинальная) ежегодная процентная ставка, при которой, если она начисляется дважды в год, результат выражается эффективной ежегодной процентной ставкой

(1.045) ² - 1 = .092925 или 9.2025% за год. Эта более высокая эффективная процентная ставка уменьшает стоимость инвестиции на $3.03.

Эффективные ежегодные процентные ставки

При m периодах компаундирования на год, эффективная годовая процентная ставка связана с установленными ежегодными процентными ставками r с периодами компаундирования, как указано ниже:



Пример Предположим, что (-$1000,$500,$700) денежные потоки дисконтированные по ставке 9%, начисляемой ежедневно на протяжении периода два года. В этом случае,


NPV = -$1000 + $500/(1+(.09/365)) ³⁶⁵ + $700/(1+(.09/365)) ^2*365 = $44.86


эффективная ежегодная процентная ставка (1+(.09/365)) ³⁶⁵ -1 = 9.42%.


Непрерывное компаундирование


Пример, предположим, что (-$1000,$500,$700) денежные потоки непрерывно компаундируемые при 9% ежегодном курсе на протяжении двух лет.



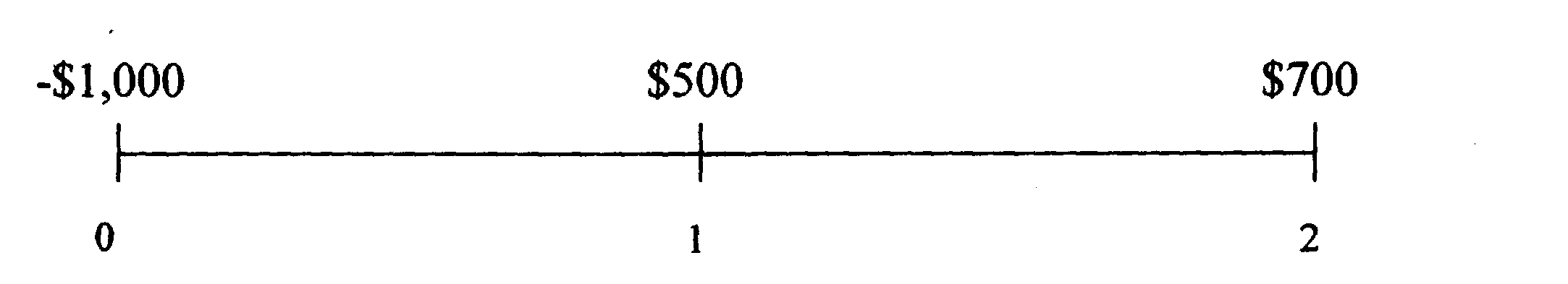
Текущая стоимость денежных потоков при непрерывном компаундировании будет:


Текущая Стоимость PV = - $1,000 + $500 (e-° °⁹) + $700 (e-^0.09*2)

= -$1,000 + $456.96 + $584.69

= $41.65


Альтернативно, для будущей стоимости ко времени t = 2:

Будущая стоимость FV = - $1,000 (e° °⁹*²) + $500 (e° °⁹) + $700

= - $1,197.28 + $547.09 + $700 = $49.87

Для проверки,

FV(e^{- rТ}) = $49.87 (e^-° °⁹*²) = $41.65 = PV

При непрерывном компаундировании, с 9% установленной ежегодной ставкой получим

Effective Annual Rate = e° °⁹ -1 = 0.0941743 => 9.41743% за год.


Проблема 3.2

Вашему сыну сегодня исполнилось 5 лет. Вы планируете начать накопление средств для его обучения в колледже равными полугодовыми депозитами на инвестиционный счет, по которому установлена ежегодная процентная ставка 9.1%, компаудирпование полугодовое с первым депозитом, который делается через 6 месяцев от настоящего времени. Вы хотите обеспечить $24,000 в год для 4 лет учебы, за год до того, когда ему будет 19 лет. Сколько денег должны вы вложить каждых шесть месяцев, пока вашему сыну исполнится 18 лет?

Решение 3.2

Стоимости на линии времени представляют тысячи долларов.




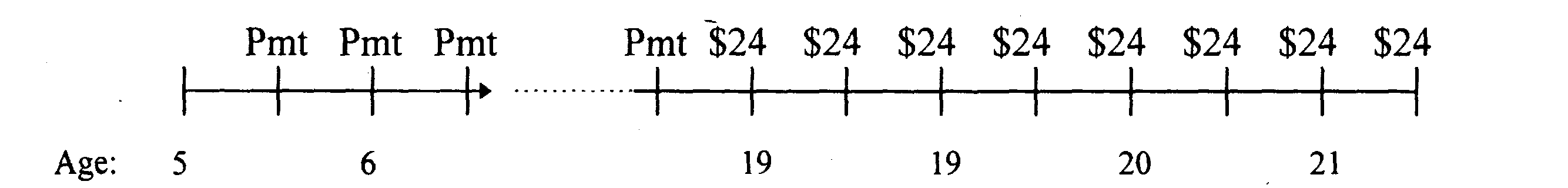
Эффективная ежегодная процентная ставка есть (1 + (.091/2))² - 1 = 9.307%. В возрасте 18, стоимость 4 извлечений со счета при 9.31% процентной ставке есть $77,232. (PMT = 24,000; n = 4; i = 9.31; вычислите PV = 77.232.16). Чтобы достичь цели, будущая стоимость депозитов в возрасте 18 должна быть равной $77,232. Необходимый полугодовой депозит есть $1,612. (FV=77,232.16; n=26; i =4.55; вычислите PMT = 1, 611.97)


Проблема 3.3

Вам 30 лет и вы желаете обеспечить вашу старость. Предположим, вы инвестируете $5000 в год при эффективной ставке доходности 9% в год на протяжении следующих 30 лет, с начальным вкладом через один год отныне. Начав, в возрасте 61, вы будете путешествовать по миру на протяжении пяти лет и будете нуждаться в сумме $X на год в начале каждого года. После того, как вы возвратитесь в U.S., вы хотите снимать $30,000 в год на протяжении следующих 15 лет. Предполагая, что 9% ставка доходности остается постоянной, какую максимальную сумму $X, вы можете потребить каждый год на протяжении вашего мирового турне?

Решение 3.3

Условимся, что временная линия стоимости представлена в тысячах долларов.



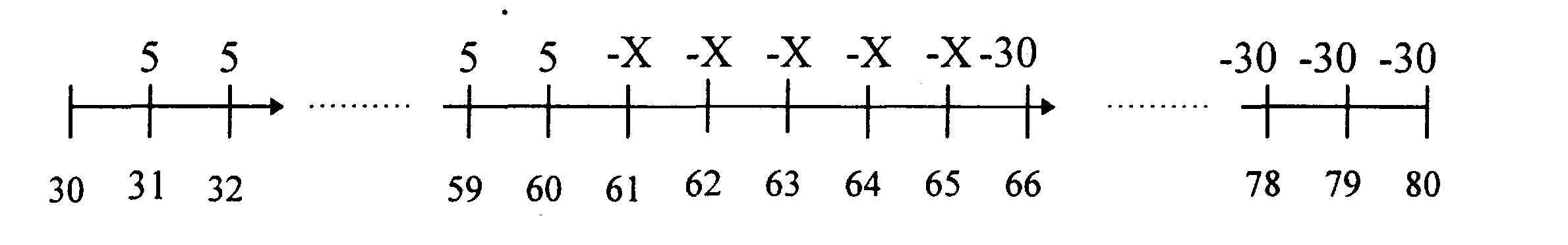
a. Стоимость $5,000 ежегодной ренты в 60 возрасте =$681,537

[PMT=5000; N=30; i=9; вычислите FV=681,537].

b. Стоимость $30,000 ежегодной ренты в возрасте 65 = $241,821

[PMT=30000; N=15; i =9; вычислите PV = 241,821].

c. Текущая стоимость $241,821 в возрасте 60 = $157,167.

[FV=241,821; N=5; i =9; вычислите PV = 157,167].

Стоимость $ X ежегодной ренты в возрасте 60 равна $681,537 - $157,167 = $524,370.

Так, $X =$134,812.

[PV=524,370; n=5; i =9; вычислите PMT == 134,812].


Основные формулы

















































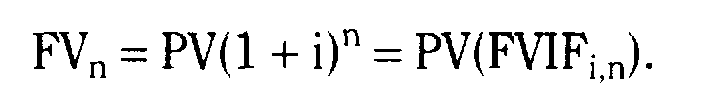
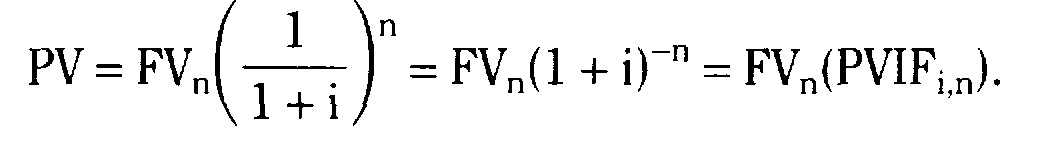
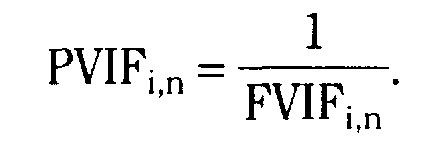
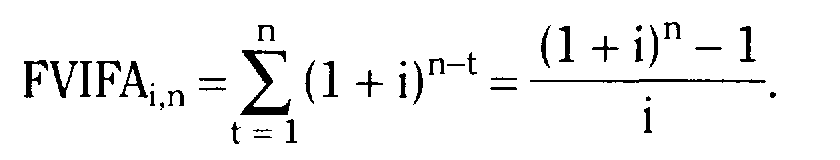
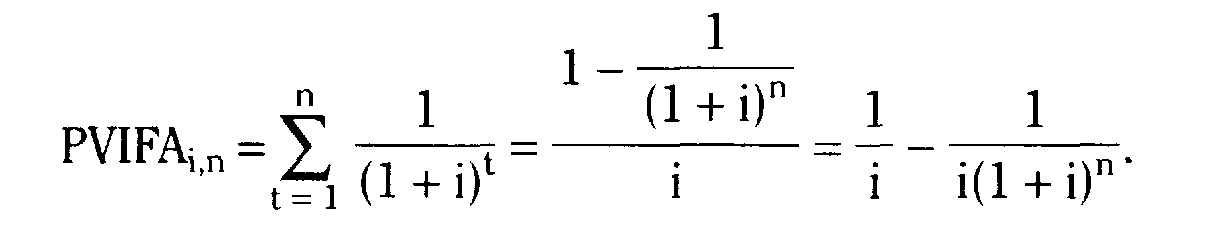
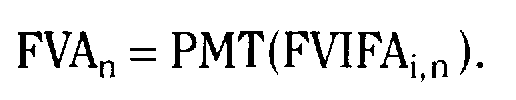
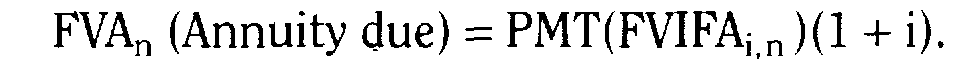
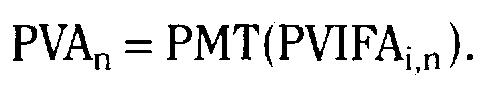
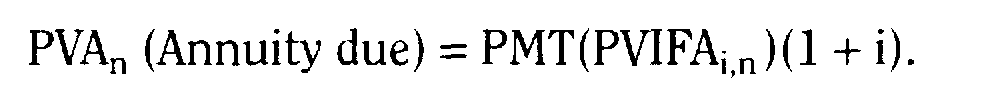
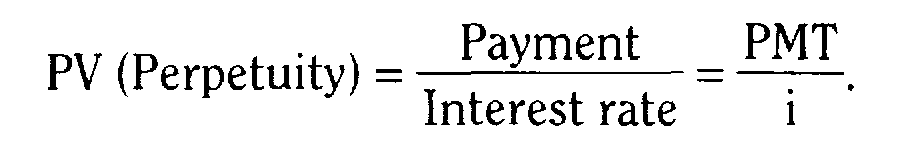
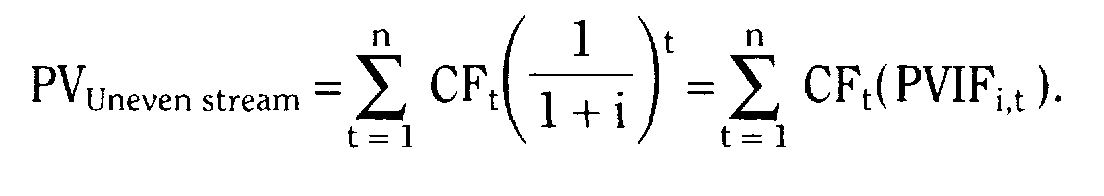
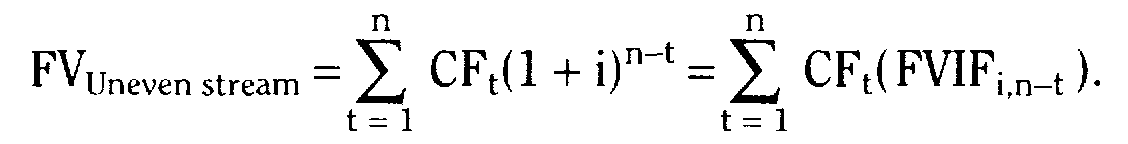
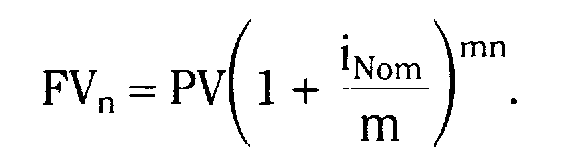
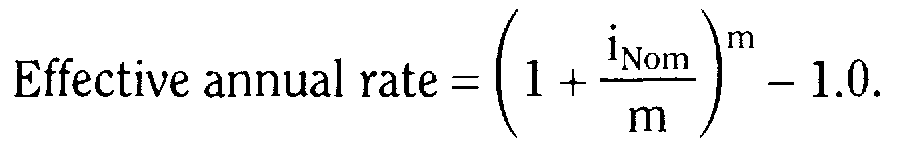
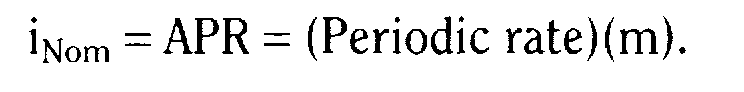
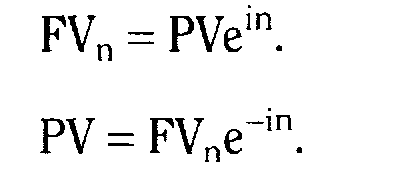
Тема 6.

Риск и ставки доходности

1. Что такое риск. Отдельный риск. Ожидаемая ставка прибыли.
   
2. Стандартное отклонение.
   
3. Коэффициент вариации.
   
4. Риск в контексте портфеля.
   
5. Связь между риском и ставками прибыли.
   
6. Коэффициент корреляции.
   
7. Риск, который диверсифицируется и рыночный риск. Диверсификация риска. Физические активы по сравнению с ценными бумагами.
   
8. Концепция беты и модель оценки капитальных активов (CAPM).
   
9. Риск в глобальном контексте.
   
10. Линия надежности рынка (SML).
    
11. Модель арбитражного ценообразования (APT).
    
12. Расчет бета - коэффициента.
    

Литература

1. Брігхем Е. Основи фінансового менеджменту: Пер. з англ. - К.: Молодь, 1997.- 1000 с. - розд. 5.
   
2. Бригхем Ю., Гапенски Л. Финансовый менеджмент : Полный курс: В 2-х т. / Пер. с англ. Под ред. В.В.Ковалева. СПб. Экономическая школа, 1998. Т.2 ХХХ+497 с. - гл.2-3.
   
3. Брейли Р., Майерс С. Принципы корпоративных финансов. Пер с англ. М.: "Олимп-Бизнес", 1997. – гл.7-8.
   
4. Financial Management: Theory and Practice, E.Brigham, L.Gapenski, M.Ehrhardt 9/e 1999.- 1087 pp +A-82.- chap.5-6.
   
5. Corporate Finance, S.Ross, R.Westerfield and J.Jaff 5/e 1999.- 869 pp. – chap. 10-11.
   
6. Foundamentals of Corporate Finance, 4/e S.Ross, R.Westerfield and B.Jordan 1997.- 720 pp. – chap. 13.