Риалы VI международной научной конференции (2-3 марта 2006 г.) Белово 2006 ббк ч 214(2Рос-4Ке) 73я431 н 34
| Вид материала | Документы |
- Г. А. Алтухова // Библиотечное дело 2007: современные технологии и ресурсы: материалы, 99.15kb.
- Состояние и перспективы развития фермерского рыбоводства аридной зоны. Тезисы докладов, 45.69kb.
- Человек язык общество материалы международной научной конференции (6 октября 2006г.), 1234.21kb.
- Российская федерация федеральный закон о государственной регистрации прав на недвижимое, 771.16kb.
- Программа 58-й научной студенческой конференции петрозаводск Издательство Петргу 2006, 841.28kb.
- Министерство образования и науки российской федерации московский государственный областной, 2810.15kb.
- Д. В. Васильев (Астраханский государственный университет), 114.29kb.
- До 1 марта 2006 года, 74.59kb.
- Прием заявок на участие и тезисов докладов до 15. 00 27 февраля 2006 года, 131.95kb.
- Правительство российской федерации постановление 20 марта 2006, 37.75kb.
Литература
- Бабинская, П.К. Настольная книга преподавателя иностранного языка: Справ. пособие / П.К. Бабинская, А.Ф. Будько, С.И. Петрова. – Мн.: Вышэйшая школа, 2001. – 522 с.
- Гальскова, Н.Д. Современная методика обучения иностранным языкам: Пособие для учителя / Н.Д. Гальскова. – М.: АРКТИ, 2004. – 192 с.
- Ильясов, И.И. Проектирование курса обучения по учебной дисциплине: Пособие / И.И. Ильясов, Н.А. Галатенко. – М.: Логос, 1994. – 208 с.
- Соловова, Е.Н. Разработка авторских программ и курсов / Е.Н. Соловова // Иностр. языки в школе. – 2004. – № 4. – С. 8-13.
УДК 004.428.4:519.214
ИСПОЛЬЗОВАНИЕ ПРОГРАММЫ MICROSOFT EXCEL
В ТЕОРИИ ПРЕДЕЛОВ
Майгула Н.В., Марасанов Ю.Н.
Ленинградский областной институт экономики и финансов, г.Гатчина
Военно–морской инженерный институт, г.Пушкин
Как известно, при изучении теории пределов рассматриваются семь видов неопределенностей:
 .
.У студентов часто возникает вопрос о том, почему же такие ситуации называются неопределенностями. С помощью стандартных средств программы Microsoft Excel на этот вопрос можно сравнительно быстро ответить.
Рассмотрим неопределенность вида
 . Для других видов неопределенностей рассуждения аналогичные. Пусть f, g, q – сходящиеся к нулю числовые последовательности, например, такие, как указано в столбцах 1, 2, 3 таблицы Excel.
. Для других видов неопределенностей рассуждения аналогичные. Пусть f, g, q – сходящиеся к нулю числовые последовательности, например, такие, как указано в столбцах 1, 2, 3 таблицы Excel.| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
 |  |  | h=f/g 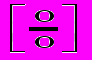 | p 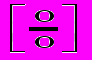 =g/f =g/f | r 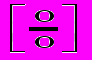 =q/f =q/f | s  =1/f =1/f | t  =1/g =1/g | w  =1/q =1/q |
| 0.1 | 0.01 | 0.5 | 10 | 0.1 | 5 | 10 | 100 | 2 |
| 0.01 | 0.0001 | 0.05 | 100 | 0.01 | 5 | 100 | 10000 | 20 |
| 0.001 | 1E-06 | 0.005 | 1000 | 0.001 | 5 | 1000 | 1E+06 | 200 |
| 0.0001 | 1E-08 | 0.0005 | 10000 | 0.0001 | 5 | 10000 | 1E+08 | 2000 |
| 1E-05 | 1E-10 | 5E-05 | 100000 | 1E-05 | 5 | 100000 | 1E+10 | 20000 |
| 1E-06 | 1E-12 | 5E-06 | 1E+06 | 1E-06 | 5 | 1E+06 | 1E+12 | 200000 |
| 1E-07 | 1E-14 | 5E-07 | 1E+07 | 1E-07 | 5 | 1E+07 | 1E+14 | 2E+06 |
| 1E-08 | 1E-16 | 5E-08 | 1E+08 | 1E-08 | 5 | 1E+08 | 1E+16 | 2E+07 |
| 1E-09 | 1E-18 | 5E-09 | 1E+09 | 1E-09 | 5 | 1E+09 | 1E+18 | 2E+08 |
| 1E-10 | 1E-20 | 5E-10 | 1E+10 | 1E-10 | 5 | 1E+10 | 1E+20 | 2E+09 |
  |   |   |  |   |  |  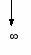 |  |  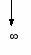 |
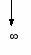
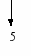
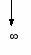
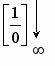
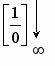
У последовательностей h=f/g, p=g/f и r=q/f числители и знаменатели стремятся к нулю. В таком случае говорят, что имеет место неопределенность вида ноль разделить на ноль:
 .
.Получить представленную выше таблицу с помощью стандартных средств программы Microsoft Excel можно очень быстро.
Из таблицы видно, что последовательности в первом, втором и третьем столбцах стремятся к нулю. При этом последовательность h=f/g в четвертом столбце, очевидно, неограниченно возрастает (стремится в бесконечность); последовательность p=g/f в пятом столбце стремится к нулю; последовательность r=q/f в шестом столбце стремится к числу 5.
Итак, если
 , то
, то  – это неопределенность, так как в зависимости от конкретного вида функций u(x) и v(x) в ответе можно получить или 0, или ∞, или С=const≠0. Поэтому говорят, что неопределенность необходимо раскрыть, используя хорошо известные специальные приемы.
– это неопределенность, так как в зависимости от конкретного вида функций u(x) и v(x) в ответе можно получить или 0, или ∞, или С=const≠0. Поэтому говорят, что неопределенность необходимо раскрыть, используя хорошо известные специальные приемы.Пределы последовательностей в столбцах 7, 8, 9, очевидно, равны бесконечности. Поэтому, если
 и С=const≠0, то
и С=const≠0, то  – это “определенность”, так как в ответе всегда получаем ∞.
– это “определенность”, так как в ответе всегда получаем ∞.Рассмотрим на примерах, как можно вычислять пределы с помощью программы Microsoft Excel.
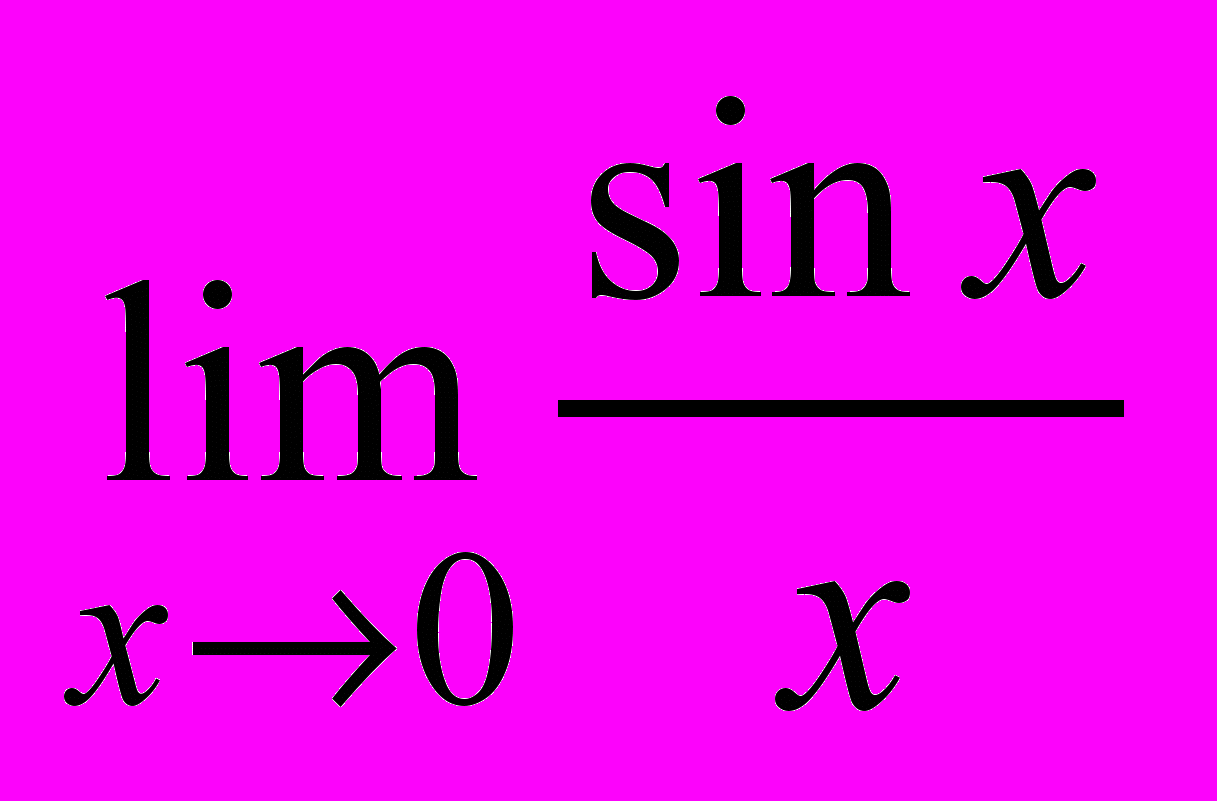
Пример 1. Вычислите предел .
Р
 ешение.
ешение.
| |
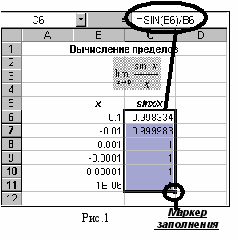
- В ячейку С6 введите формулу =sin(B6)/B6 (рис.1) и протяните мышью маркер заполнения вниз до ячейки С11.
Последовательность значений, полученных в диапазоне ячеек С6:С11, показывает, что искомый предел равен 1.
Ответ: 1.
Пример 2. Вычислите предел

Решение.
Выполните пункты 1 – 3 примера 1.
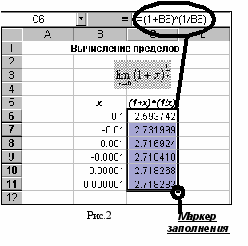
| В ячейку С6 введите формулу =(1+В6)(1/В6) (рис.2) и протяните мышью маркер заполнения вниз до ячейки С11. Последовательность значений, полученных в диапазоне ячеек С6:С11, показывает, что искомый предел приближенно равен 2,718, т.е. числу е. Ответ: е. | |
Пример 3. Вычислите левосторонний предел

Решение.
- В ячейку А6 введите число 0,1.
- В ячейку А7 впишите формулу =А6*0.1.
- Протяните маркер заполнения от ячейки А7 до ячейки А12.
- В ячейку В6 введите формулу =1-А6 (рис.3) и протяните мышью маркер заполнения вниз до ячейки В13. Получаем последовательность значений переменной х, стремящихся к единице слева.
- В ячейку С6 введите формулу =(В62-4*B6+3)/(B62-1) (рис.4) и протяните мышью маркер заполнения вниз до ячейки C13.
- Последовательность значений, полученных в диапазоне ячеек С6:С13, показывает, что искомый предел равен -1.

 | |
Ответ: -1.
Пример 4. Вычислите предел
 .
.Р
 ешение.
ешение.
| Последовательность значений, полученных в диапазоне ячеек B6:B12, показывает, что искомый предел равен –0. Ответ: –0. |
Литература
- Сдвижков О.А. Математика в Excel 2002. М.: СОЛОН-Пресс, 2004.
УДК 378.147.88:531
ПРОГРАММИРОВАНИЕ ДАТЧИКОВ И ОПЫТЫ
С НИМИ В КУРСЕ МЕХАНИКИ
Майер Р.В.
Глазовский государственный педагогический институт
Применение информационных технологий при изучении физики существенно расширяет возможности преподавателя, позволяя ему использовать современные методы исследования и сочетать теоретическое изучение явлений с натурным и вычислительным экспериментом. Компьютер –– многофункциональное устройство, которое может быть использовано: а) в качестве источника сигналов или измерительного прибора; б) для обработки файлов, полученных на других устройствах (сканерах, фото– и видеокамерах и т.д.); в) для математической обработки результатов измерений и построения графиков, диаграмм и т.д.; г) для компьютерного моделирования и проведения вычислительного эксперимента.
В статье рассматривается методика использования универсального прибора, состоящего из персонального компьютера (ПК) , к которому через параллельный порт LPT, обычно используемый для соединения с принтером, подключаются различные датчики (геркон, оптодатчик и датчик координаты). Перед студентами, выполняющими соответствующий опыт, стоит задача изучить имеющуюся или написать новую программу, обрабатывающую сигналы с используемого датчика и определяющую длительность какого-либо процесса, время между двумя срабатываниями, частоту генерируемых импульсов или другую физическую величину. Все перечисленные ниже задания были неоднократно апробированы в различных демонстрационных экспериментах, на лабораторных работах физического практикума, при выполнении курсовых и дипломных работ. Для программирования датчиков нами использовались языки QBasic и Pascal, но в статье приводятся программы на языке QBasic.
Общие принципы использования параллельного интерфейса для обмена информацией с внешними устройствами и конкретные примеры программ рассмотрены в [1, 2, 3]. В нашем случае питание датчика осуществлялось от компьютера. В качестве общего провода используется один из 18, 19, 20, … 25 выводов параллельного интерфейса LPT. Проводом питания + 5 В служит 2, 3, 4, 5, 6, 7, 8 или 9 вывод. Для этого в начале программы, обрабатывающей сигналы с датчика, с помощью команды OUT &H378, 255 в ячейку памяти 378h записывают число 255, что соответствует двоичному числу 11111111. При этом на выводах 2––9 порта LPT появляется напряжение высокого уровня, соответствующее логической 1, которое и используется для питания датчика. Совокупность 8 логических нулей и единиц, снимаемых с выводов 10, 11, 12, 13, 14, 15, 16 и 17 порта LPT, записывается в ячейку памяти с адресом 379h. Если сигнал с формирователя импульсов подается на один из перечисленных выводов параллельного интерфейса, то в этой ячейке памяти при различных состояниях датчика будут записаны различные числа. Для считывания информации из порта LPT используется оператор INP(&H379). Оператор TIMER возвращает время, отсчитанное по системным часам ПК. Ниже представлена система экспериментальных заданий, выполняя которые, студенты знакомятся с различными видами датчиков, их подключением и использованием в учебном эксперименте по механике.

1. ИЗУЧЕНИЕ МАГНИТОКОНТАКТНОГО ДАТЧИКА (ГЕРКОНА)
Геркон (герметичный контакт) –– стеклянный баллон с двумя ферромагнитными контактами, которые замыкаются при поднесении магнита. Подключим геркон к параллельному порту LPT, используя выводы 11 и 25 (рис. 1). Вдали от магнита геркон незамкнут, на всех выводах порта логическая 1, поэтому в ячейке памяти с адресом H379 находится число 11111111 (255). При поднесении магнита соответствующий вывод LPT порта замыкается на общий, на нем появляется логический 0. В ячейку памяти H379 помещается число 01111111 (127), которое может быть считано командой x = INP(&H379).
CLS : x = INP(&H379) 'ПРОГРАММА 1
WHILE INKEY$ = "" 'Начало цикла 1: Пока не нажат пробел
WHILE x = 255: x = INP(&H379): PRINT "1"; : WEND 'Цикл 1.1
WHILE x = 127: x = INP(&H379): PRINT "0"; : WEND 'Цикл 1.2
WEND 'Конец цикла 1
END
Опыт 1.1. Тестирование геркона. Наберите программу 1, к порту LPT подключите геркон. Запустите программу и поднесите к геркону магнит. Пронаблюдайте, как на экране компьютера 0 сменяется на 1 и наоборот. Пока геркон замкнут, x равно 225, программа вращается в цикле 1.1, печатая на экране "1". Пока геркон разомкнут, x равно 127, программа вращается в цикле 1.2, печатая на экране "0". Затем все многократно повторяется (цикл 1). При нажатии на клавишу клавиатуры компьютер выходит из цикла .
CLS : x = INP(&H379) 'ПРОГРАММА 2
WHILE x = 127: x = INP(&H379) 'НАЧАЛО ЦИКЛА 1
PRINT "ОЖИДАНИЕ "
WEND 'КОНЕЦ ЦИКЛА 1
t0 = TIMER
WHILE x = 255: x = INP(&H379) 'НАЧАЛО ЦИКЛА 2
PRINT "ГЕРКОН ЗАМКНУТ"
WEND 'КОНЕЦ ЦИКЛА 2
t = TIMER
PRINT "ВРЕМЯ ЗАМЫКАНИЯ ", t - t0
END
Опыт 1.2. Измерение времени замыкания геркона. Наберите программу 2 и запустите ее. Сначала ПК находится в режиме ожидания (цикл 1), на экране –– сообщение "ОЖИДАНИЕ". При поднесении магнита ПК выходит из цикла 1, переменной T0 присваивается текущее время ПК, программа начинает вращаться в цикле 2, печатая на экране сообщение "ГЕРКОН ЗАМКНУТ". Удалите магнит, –– переменной T присваивается время ПК, соответствующее моменту размыкания геркона, время замыкания T-T0 выводится на экран. Измерьте время замыкания геркона с помощью секундомера и компьютера, сравните полученные результаты.
Опыт 1.3. Измерение времени между последовательными замыканиями. Самостоятельно напишите программу и запустите ее. К геркону поднесите магнит, удалите его и через время 5––20 с, отсчитанное по секундомеру, снова поднесите. На экран компьютера должно выводиться время между последовательными замыканиями. Сравните результаты.
2. ИЗУЧЕНИЕ ОПТОДАТЧИКА
Оптодатчик состоит из инфракрасного светодиода, напротив которого установлен фотодиод, подключенный к формирователю сигнала. При затемнении и освещении фотодиода на выходе формирователя сигнала резко меняется напряжение: логическая 1 сменяется логическим 0 или наоборот. Зная время пересечения светового пучка оптодатчика или время между двумя последовательными пересечениями можно определить скорость тела. Питание оптодатчика осуществляется от 3 и 25 выводов порта LPT, для чего по адресу H378 записывают 255.
OUT &H378, 255 ''ПРОГРАММА 3
WHILE INKEY$ = "" 'ЦИКЛ 1
x = INP(&H379): WHILE x = 255: x = INP(&H379): PRINT "1"; 'ЦИКЛ 1.1
WEND
t0 = TIMER: WHILE x = 127: x = INP(&H379): PRINT "0"; 'ЦИКЛ 1.2
WEND
t = TIMER: PRINT t - t0 'ПЕЧАТЬ ВРЕМЕНИ ПЕРЕСЕЧЕНИЯ ПУЧКА
WEND 'КОНЕЦ ЦИКЛА 1
END
Опыт 2.1. Тестирование оптодатчика. Подключите оптодатчик, наберите программу 3 и запустите ее. Программа содержит цикл 1, в котором находятся вложенные циклы 1.1 и 1.2. Если в порт LPT поступает число 11111111 (225), то программа вращается в цикле 1.1 и на экране печатается "1". Если в порт LPT поступает число 01111111 (127), то программа вращается в цикле 1.2, на экран выводится "0". Пересекая световой пучок, убедитесь в том, что программа работает описанным выше образом.
Опыт 2.2. Измерение времени пересечения светового пучка. Загрузите программу 3, закомментируйте операторы PRINT "0" И PRINT "1". Когда при перекрывании светового пучка программа выйдет из цикла 1.1, переменной T0 будет присвоено текущее время ПК. Пока фотодиод затемнен, программа вращается в цикле 1.2. При освещении фотодиода программа выходит из цикла 1.2 и теперь переменной T присваивается текущее время ПК. Разность T-T0 выводится на экран ПК, после чего все повторяется снова (цикл 1) до нажатия на пробел. Измерьте время затемнения фотодиода с помощью секундомера и сравните его с результатом, выдаваемым ПК.
Опыт 2.3. Измерение времени между двумя последовательными пересечениями светового пучка. Самостоятельно напишите программу, которая ждет первого затемнения оптодатчика, после чего присваивает переменной T0 текущее время по часам ПК, затем ждет второго пересечения оптодатчика и соответствующее время присваивает переменной T. Разность T-T0 должна выводиться на экран. Запустите программу, измерьте время между последовательными пересечениями оптодатчика с помощью секундомера и ПК, сравните результаты.
3. ИЗМЕРЕНИЕ УГЛОВОЙ КООРДИНАТЫ ТЕЛА
Для измерения координаты можно использовать резистивный датчик, сопротивление которого зависит от положения подвижного контакта. Установка состоит из релаксационного RC––генератора, который выдает прямоугольные импульсы (чередующиеся логический 0 и логическая 1). Частота этих импульсов зависит от сопротивления резистора, который одновременно может являться датчиком координаты. Чем меньше сопротивление резистора, тем быстрее происходит заряд или разряд конденсатора, соответственно выше частота импульсов. Сигнал с RC–генератора поступает в ПК, который в течение заданного времени
 с считает количество поступивших импульсов, тем самым определяя их частоту. Результаты подсчета импульсов выводятся на экран в графическом виде или в числовом формате, либо записываются в файл.
с считает количество поступивших импульсов, тем самым определяя их частоту. Результаты подсчета импульсов выводятся на экран в графическом виде или в числовом формате, либо записываются в файл.SCREEN 2: LINE (10, 180)-(640, 180): LINE (10, 0)-(10, 480) ''ПРОГРАММА 4
OUT (888), 255: M = .2 'M - Масштаб по ОY
WHILE INKEY$ = ""
j = 0: dt = 1: t0 = TIMER: t = t0 + .01
WHILE t - t0 < dt
x = INP(889): 'PRINT 'СОСТОЯНИЕ ПОРТА ', x;
IF (y = 127) AND (x = 255) THEN j = j + 1
y = x: t = TIMER
WEND
j = M * (j - 80): tt = tt + dt
LINE (10 + tt * 5, 180 - j / dt)-(10 + (tt - dt) * 5, 180 - jj / dt)
LINE (11 + tt * 5, 181 - j / dt)-(11 + (tt - dt) * 5, 181 - jj / dt)
jj = j: 'PRINT 'КООРДИНАТА ', j / dt;
WEND
END
Опыт 3.1. К ПК подключите формирователь сигнала с датчиком координаты. Наберите программу 4 и запустите ее. Медленно поворачивая подвижный контакт резистора, пронаблюдайте получающуюся кривую зависимости координаты от времени.
Опыт 3.2. Повторите предыдущий опыт, изменив время счета импульсов
 , масштаб M. Измените программу так, чтобы она через заданное время
, масштаб M. Измените программу так, чтобы она через заданное время  выводила координату в числовом виде.
выводила координату в числовом виде.4. ИСПОЛЬЗОВАНИЕ ДАТЧИКОВ В УЧЕБНОМ ЭКСПЕРИМЕНТЕ ПО МЕХАНИКЕ
ПК соединенный с одним из рассмотренных выше датчиков при наличии соответствующей программы становится универсальным прибором, позволяющим измерять длительность исследуемого процесса, подсчитывать количество импульсов за заданный промежуток времени, вычислять скорость движения и координату, строить графики. Ниже рассмотрены лишь некоторые примеры использования ПК в учебном эксперименте по механике.
Опыт 4.1. Изучение вращения Сегнерова колеса с помощью геркона. Экспериментальная установка состоит из Сегнерова колеса, выполненного в виде подвешенной на нити пластиковой бутылки с двумя изогнутыми трубками. К боковой поверхности бутылки приклеены два постоянных магнита, а рядом с ней расположен геркон так, что при вращении бутылки происходит его срабатывание. Геркон подключают к ПК и запускают программу, периодически определяющую время замыкания геркона и скорость вращения Сегнерова колеса. Результаты измерений могут выводиться на экран в текстовом и графическом виде или сохраняться в файле. Под действием реактивной силы Сегнерово колесо набирает скорость, закручивая нить, останавливается и начинает вращаться в противоположную сторону, совершая затухающие колебания.
Опыт 4.2. Изучение реактивного движения Сегнерова колеса с помощью оптодатчика. Соберите установку, состоящую из подвешенной на нити двухлитровой пластиковой бутылки с двумя изогнутыми трубками, к горлышку которой прикреплен диск с прорезями по краю. В верхней части бутылки имеется отверстие для воздуха. Вблизи края диска установите оптодатчик, подключенный к параллельному порту ПК. При вращении бутылки с диском происходит периодическое освещение и затемнение фотодиода, в результате чего в компьютер поступает последовательность логических 0 и 1, которая обрабатывается соответствующей программой написанной на языке Pascal или Qbasic [3, 4]. Результаты измерений скорости вращения в последовательные моменты времени выводятся на экран в цифровом или графическом виде. Запустите Сегнерово колесо и получите на экране компьютера график зависимости скорости колеса от времени.
Опыт 4.3. Изучение движения системы с одной степенью свободы. К неподвижному блоку прикрепите диск с прорезями, а рядом установите оптодатчик так, чтобы прорези при вращении диска пересекали световой пучок оптодатчика, периодически открывая и закрывая фотодиод. На блок намотайте нить, к концу которой привяжите тело. На ПК запустите программу, считающую количество импульсов в единицу времени с выхода оптодатчика. Отпустите груз и получите на экране монитора график зависимости угловой скорости диска от времени. Проведите серию опытов при различных массах груза.
Опыт 4.4. Вращение тела в вязкой среде. В центре алюминиевого диска с прорезями прикрутите стальной болт, за который подвесьте диск к постоянному магниту так, чтобы он вращался вокруг вертикальной оси, оставаясь в горизонтальной плоскости [2]. На диск наденьте крыльчатку, увеличивающую влияние силы сопротивления, действующей со стороны воздуха. Под диском расположите магнитный движитель, состоящий из двух обмоток на U-образном сердечнике, одна из которых замкнута накоротко, а другая подключена к ЛАТРу. Вблизи края диска установите соединенный с ПК оптодатчик так, чтобы при вращении диска прорези пересекали световой пучок. Запустите на ПК программу, определяющую количество прорезей, прошедших мимо оптодатчика за 1 c, вычисляющую угловую скорость и строящую график ее зависимости от времени. Проведите серию опытов, включая и выключая движитель, подавая на него различные напряжения и поворачивая его так, чтобы изменялось направление вращающего момента, действующего на диск.
Опыт 4.5. Затухающие колебания физического маятника. Соберите установку, состоящую из физического маятника, выполненного в виде металлической пластины с флажком на конце, и оптодатчика, подключенного к ПК. Оптодатчик должен быть расположен под точкой подвеса так, чтобы проходя положение равновесия, маятник пересекал световой пучок. Напишите программу, измеряющую время пересечения светового пучка и определяющую скорость прохождения маятником положения равновесия. Результаты измерений амплитуды скорости должны сохраняться в файле и выводиться на экран в текстовом или графическом виде. Убедитесь в том, что графиком зависимости амплитуды скорости от времени в случае затухающих колебаний является экспонента.
Опыт 4.6. Изучение нелинейности колебаний физического маятника [5]. Используется программа, измеряющая время между двумя пересечениями оптодатчика. Соберите установку, состоящую из физического маятника, вблизи положения равновесия которого расположен оптодатчик (опыт 4.5). Отклоните маятник от положения равновесия и отпустите, –– на мониторе ПК будет выведена длительность половины колебания. Несколько раз повторите опыт, отклоняя маятник на 10 – 90 градусов от вертикали и убедитесь в том, что период колебаний с ростом амплитуды увеличивается. Это доказывает, что при большой амплитуде колебания физического маятника нелинейны.
Опыт 4.7. Затухающие колебания крутильного маятника. На длинной нити подвесьте осесимметричое тело (например, пластиковую бутыль с водой), к которому прикреплен диск с прорезями по краю. Рядом с краем расположите оптодатчик, соединенный с ПК. Закрутите тело и отпустите его так, чтобы оно совершало крутильные колебания. Период колебаний должен быть не менее 10 с. Запустите программу, подсчитывающую число прорезей, проходящих мимо оптодатчика, и строящих график зависимости модуля угловой скорости от времени. Изучите получающиеся кривые, исследуйте затухающие колебания.

 ). В результате в блоке ячеек В6:В11 запишется последовательность значений х, стремящихся к нулю.
). В результате в блоке ячеек В6:В11 запишется последовательность значений х, стремящихся к нулю.