Российская академия образования Институт научной информации и мониторинга

Вид материала

Документы

Содержание Сложные задачи Треугольник и его элементы. Виды треугольников Медианы, биссектрисы и высоты треугольника. Площадь треугольника Частные виды параллелограмма Координатная прямая Расстояние между точками на координатной прямой Координатная плоскость Углы и действия с ними Измерение углов Построение углов Действия с углами Многогранники и их элементы Олимпиады по геометрии для 3 класса

Подобный материал:

• Доклад на Всероссийской научной конференции «От СССР к рф: 20 лет итоги и уроки», 140.15kb.
• Из истории российского образования, 1157.84kb.
• Управление образованием, 733.04kb.
• Государственная академия наук российская академия образования институт семьи и воспитания, 5970.09kb.
• Государственная академия наук российская академия образования институт семьи и воспитания, 2933.75kb.
• Государственная академия наук российская академия образования институт семьи и воспитания, 3113.4kb.
• Государственная академия наук российская академия образования институт семьи и воспитания, 3011.43kb.
• Государственная академия наук российская академия образования институт семьи и воспитания, 4091.81kb.
• Государственная академия наук российская академия образования институт семьи и воспитания, 3731.34kb.
• Ханнанов Наиль Кутдусович, Институт научной информации и мониторинга рао, e-mail: khann@dio, 244.27kb.

Контрольные вопросы.

1. Покажите поверхность стола, доски, стены, стула и т.д. Как называются такие поверхности? Э. Эбботт придумал назвать такую поверхность Флатландией. Кто живет во Флатландии? В виде чего они видят друг друга?


2. Покажите поверхность моря рукой или с помощью листка бумаги. Приведите еще примеры кривых поверхностей. Как называется поверхность шара? Многие поверхности не имеют названия, поэтому их так называют, например, поверхность куба. Нарисуйте в тетради развертки поверхностей куба, параллелепипеда, конуса, цилиндра.


4. Название каких геометрических тел знаете?

5. Изобразите такие геометрические тела: куб, прямоугольный параллелепипед, конус, шар, цилиндр. Могут ли эти тела жить в Лайнландии и Флатландии? Сколько измерений они имеют? Как вычислить площадь поверхности куба, прямоугольного параллелепипеда? Как вычислить их объем? Изобразите три проекции тела на плоскость.


Сложные задачи:

а) Треугольный лист бумаги (остроугольный треугольник),

б) Квадратный лист бумаги. Сложите его так, чтобы получилась поверхность треугольной пирамиды.

в) Какую поверхность образует прямая линия в результате вращения? Сделайте модель этих поверхностей с помощью листа бумаги.

г) Почему можно еще нарисовать одну стрелку в цепи точка ® линия ® поверхность?

д) Что отличает «жителей» поверхности от «жителей» линий?


Итак, осталось поставить последнюю стрелку в этой цепочке точка ® линия ® поверхность ® тело. Как же поверхность связана с телом?

Какое же отношение к этой цепочке имеет ряд чисел 0, 1, 2, 3?


ТРЕУГОЛЬНИК И ЕГО ЭЛЕМЕНТЫ.


ВИДЫ УГЛОВ.


1. а) Начертите фигуру, являющуюся частью плоскости, ограниченную двумя лучами с общим началом. Закрасьте эту часть плоскости или выделите дугой. Как называется эта фигура? Как ее обозначить?

б) Что изображено на рисунке? Какой угол является большим?




(Хорошо углы показывать ладонями: чем больше раскрыты ладони, тем и угол больше).


в) Нарисуйте угол. Нарисуйте угол, больше данного и угол меньший данного.


Перечислите виды углов. Как начертить прямой угол в тетради в клетку, на нелинованном листке?


2. Как перегибанием листа бумаги получить прямой угол? Начертите острый и тупой углы. Как проверить себя? Какой угол называется острым, тупым?

Знаете ли вы, что в Древнем Египте геометры строили прямой угол: деля веревку со связанными концами на 12 равных частей и, придавая этой веревке форму треугольника, стороны которого соответственно равны 3,4 и 5 частям, получали прямоугольный треугольник.


3. В тетради постройте два прямых угла так, чтобы в пересечении образовался прямоугольник.


Какие фигуры могут получаться в пересечении двух углов?


4. Перечертите угол и определите его вид (рис.). Проведите луч, разбивающий его на два угла, один из которых острый, а другой прямой.





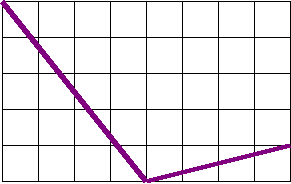
5. Вырежьте из бумаги три угла: острый, тупой, прямой. Чтобы не перепутать вырезанную фигуру с треугольником, край сделайте волнистым.





Являются ли углы симметричными фигурами? Как без карандаша и линейки «провести» ось симметрии угла?

Ось симметрии угла называют биссектрисой. Биссектриса угла – это луч, который делит угол пополам.

В слове «биссектриса» корень сектр, а приставка – бис, что означает «дважды».Отсюда вытекает определение равных углов: как углов, которые при наложении совпадают.


6. Перечислите углы в тетрадь, определите их вид и постройте биссектрису каждого из них.











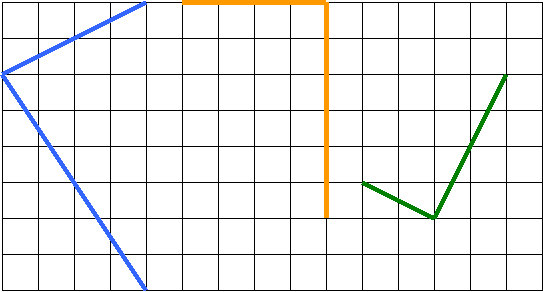
7. Постройте угол, определите его вид и постройте два луча, разбивающие данный угол на три равные части.





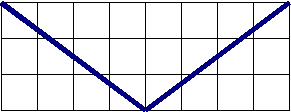
8. На рис. изображены углы. Перерисуйте их, обозначьте и определите их вид. Для каждого из них постройте угол, симметричный относительно заданной пунктирной прямой.








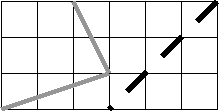
9. Нарисуйте угол. Из его вершины проведите луч внутри угла. Сколько углов на этом рисунке? Ответьте на этот же вопрос, если провести два таких луча? Три таких луча? А если провести 10 лучей?

Результаты надо записать в таблицу:

Кол-во лучей	Кол-во углов
2	1
3	3
4	6

Что общего с задачей о количестве отрезков, образуемых в результате выбора точек на прямой?


ВИДЫ ТРЕУГОЛЬНИКОВ


1. Отметьте три точки А, В и С, не лежащие на одной прямой. Соедините их отрезками АВ, ВС. СА. Часть плоскости, ограниченная этими тремя отрезками, называется треугольником. Как называются точки А, В, С? Как называются отрезки АВ, ВС, АС? Назовите углы треугольника. Определите вид углов вашего треугольника. У кого получились все углы острыми? Такие треугольники называются остроугольными. У кого получился треугольник с прямым углом? Такие треугольники называются прямоугольными. У кого получился треугольник с тупым углом? Такие треугольники называются тупоугольные.


а) Дорисуйте в вашей тетрадке другие два вида треугольников.

У любого треугольника есть два острых угла.


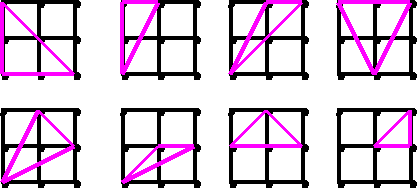
2. Начертите разные треугольники в девятиточечном квадрате. Определите вид треугольников. Обозначьте прямые и тупые углы. Каких треугольников больше?





Стороны прямоугольных треугольников, образующие прямой угол, называются катетами, а сторону, противолежащую прямому углу, называют гипотенузой.


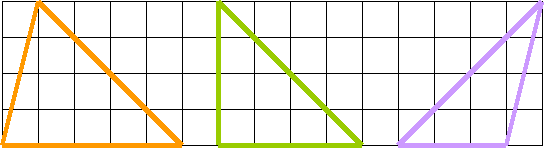
3. Покажите все треугольники. Определите их вид.





4. Начертите три вида треугольников: остроугольный, прямоугольный, тупоугольный в тетради в клетку и на нелинованном листе бумаги.


5. Начертите остроугольный треугольник. Разбейте его на два треугольника. Определите вид каждого. Можно ли остроугольный треугольник разбить на два остроугольных треугольника? Можно ли прямоугольный треугольник разбить на два остроугольных, тупоугольный треугольник разбить на два остроугольных? Какую гипотезу можно построить?


6. Начертите остроугольный, тупоугольный и прямоугольный треугольники. Разбейте каждый на два прямоугольных треугольника. Какую гипотезу можно сформулировать?

7. Отрезок, разбивающий треугольник на прямоугольные, называют высотой. Перечертите DАВС. В каждом проведите высоту АН.





Интересны два последних случая, которые дополнят определение высоты: высота треугольника может не разбивать его на два прямоугольных треугольника, она может совпадать со стороной треугольника, если он прямоугольный или «падать» на продолжение стороны, если треугольник тупоугольный, но в этом случае все равно образуются два прямоугольных треугольника.


8. Разрежьте квадрат на три треугольника, чтобы среди них были: один – остроугольный, один – прямоугольный, один тупоугольный.


9. Начертите остроугольный, тупоугольный и прямоугольный треугольники, у которых 2 стороны соответственно равны 3 см и 5 см. Измерьте третью сторону.

Опишите свойства треугольника

Треугольник является равнобедренным, т.е. у него есть пара равных сторон.


10. Начертите равнобедренный и тупоугольный треугольники, равнобедренный и прямоугольный треугольник в тетради в клетку и на нелинованном листе. Выделите равные стороны треугольников одним цветом. Эти выделенные стороны называются боковыми, а третью сторону – основанием.


11. Начертите треугольник, у которого все стороны равны. Какой инструмент понадобится? Как называется такой треугольник? Сколько осей симметрии может иметь треугольник? Начертите треугольник с одной осью симметрии, с тремя осями и ни одной. В каждом случае определите вид треугольника.


12. Определите вид треугольника:





13. Начертите: а) DАВС, у которого АВ=ВС = 6 см. определите вид треугольника. Вычислите его периметр; б) DКМN : ÐК – прямой, МN – 5 см.; в) DRТО – тупоугольный, ТR = 8 см 3 мм

14. Рассмотрите равнобедренный треугольник.





Что надо у него измерить, чтобы вычислить его периметр?

Формула периметра Р = 2а + в.


15. В равнобедренном треугольнике боковая сторона 7, а основание 4. Вычислите периметр.


16. В равнобедренном треугольнике боковая сторона 7, Р = 17. Вычислите основание.


17. Постройте прямоугольный треугольник, гипотенуза которого равна 6 см.


18. Перечертите треугольник (рис.) Постройте еще один треугольник, равный исходному, одна из сторон которого задана на рисунке. Определите вид треугольника.





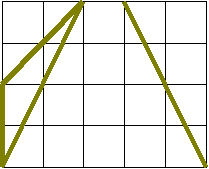
19. Перечертите треугольник. Определите его вид. На каждой из его сторон постройте по треугольнику равному исходному.




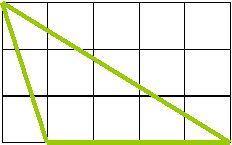
20. Перечертите треугольник (рис.) Определите вид. Разбейте его на 4 равных треугольника.





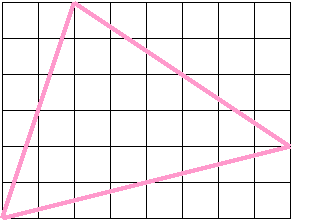
21. На какие треугольники разбивает диагональ прямоугольник? Квадрат?


22. Вырежьте из бумаги остроугольный, прямоугольный и тупоугольный треугольники. Как, не прибегая к линейке, найти середину каждой из их сторон?

Отметьте середины сторон каждого треугольника и соедините их по линейке. Что интересного замечаете?




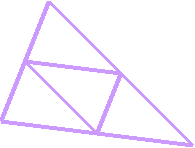
Выводы: 1) 4 треугольника равны между собой. 2) Стороны маленького треугольника в 2 раза меньше сторон большого. 3) Углы маленького треугольника равны углам большого. 4) Стороны маленького треугольника параллельны сторонам большого треугольника. 5) площадь маленького в 4 раза меньше площади большого треугольника.


Согните треугольник по начерченным линиям. Что получается?


Получается треугольная пирамида. Получили ее только из остроугольного треугольника.


Сколько граней, вершин, ребер у треугольной пирамиды? Можно изобразить треугольную пирамиду в тетради в клетку.


23. Ученик нарисовал на доске треугольник и отметил середину его сторон. Затем треугольник стерли, но отмеченные точки остались. Нельзя ли восстановить треугольник?


24. Нарисуйте равносторонний треугольник. Отрезками разбейте его на: а) два прямоугольных треугольника, б) на три прямоугольных треугольника.


МЕДИАНЫ, БИССЕКТРИСЫ И ВЫСОТЫ ТРЕУГОЛЬНИКА.


1. Вы умеете путем перегиба листа «строить» биссектрису угла. Постройте таким же образом биссектрисы углов треугольника. Что вы замечаете?


Попытайтесь так, как в первом задании, без линейки «провести» еще один отрезок, который называется медианой. Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны треугольника. Сколько можно провести медиан в треугольнике? Каким свойством они обладают?


2. Одним из интересных отрезков, «живущих» в треугольнике, является высота. Треугольник похож на силуэт горы. Покажите высоту «горы» - треугольника ,изображенного на рисунке. Как ее построить? Высота – это отрезок, «падающий» под прямым углом на противоположную сторону.




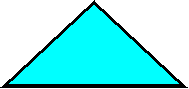
3. А если нарисован тупоугольный треугольник.

Его высота «падает» на продолжение стороны. Сколько высот можно провести в треугольнике? Потренируйтесь проводить высоты в тетрадях в клетку. Можно проводить по одной высоте, «удобной» для построения без чертежного угольника.

4. На какие треугольники разбивает высота данный треугольник?




5. Постройте равнобедренный треугольник. Проведите к его основанию высоту, медиану, биссектрису. Что можно сказать?


В треугольнике АВС высота ВН является медианой и ее длина равна 2 см. Найдите периметр DАВС, если периметр DАВН = 10 см.


ПЛОЩАДЬ ТРЕУГОЛЬНИКА


1. Начертите прямоугольный треугольник. Как найти его площадь?





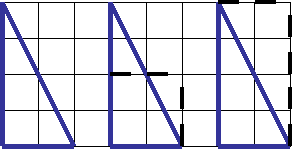
Формула площади прямоугольного треугольника имеет вид S = а × в : 2, где а и в катеты или эту формулу можно прочитать иначе: половина произведения высоты на сторону, на которую «падает» эта высота.


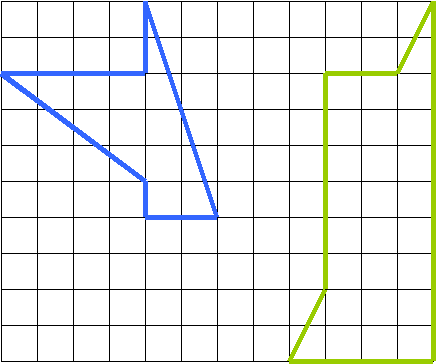
2. Зная формулу площади прямоугольного треугольника, найдите площади следующих фигур, предварительно указав – какие длины отрезков вам необходимо знать для вычисления площади фигур.





3. Вырежьте из бумаги прямоугольный треугольник и попросите соседа вычислить его площадь.

4. Вырежьте из бумаги два прямоугольных треугольника, составьте из них интересную фигуру и найдите ее площадь.


5. Постройте в тетради прямоугольный треугольник с катетами 4 кл и 2 кл. От каждой из его сторон постройте по квадрату. Что интересного замечаете?


6. Площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. Этот факт был известен грекам до н.э. Но доказательство его приписывают Пифагору. Любопытным детям можно дать задание проверить для другого вида прямоугольных треугольников этот факт.


7. Перечертите треугольник. Определите его вид. Вычислите площадь.





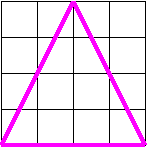
I способ – разделить его на два прямоугольных треугольника а : 2 × h × 2 + а : 2 × h: 2

II способ – перекроить в прямоугольник а : 2 × h

III способ – дополнить до прямоугольника а × h : 2

Все три формулы равносильны Площадь данного треугольника находится также, как и площадь прямоугольного треугольника –полупроизведением высоты и основания.


8. Перечертите треугольник. Определите его вид. Вычислите его периметр и площадь. Напишите формулу его площади.





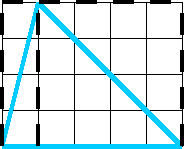
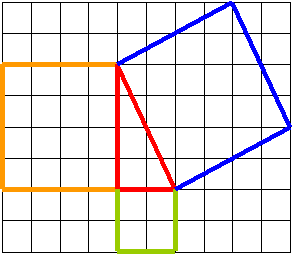
9. Найдите площади фигур.




10. Вырежьте остроугольный, тупоугольный треугольники. Вычислить их периметр и площадь.


11. Начертите остроугольный, прямоугольный, тупоугольный треугольники, площадь которых 1 кв см.


12. Вычислите площадь фигуры. Разверткой поверхности какого тела она является?




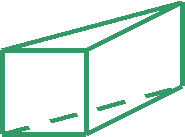
13. Как сделать прямоугольную призму. Нарисуйте развертку поверхности призмы, вырежьте.. Вычислите площадь поверхности призмы, объем .





ПАРАЛЛЕЛОГРАММЫ


1. Как могут располагаться две прямые на плоскости?

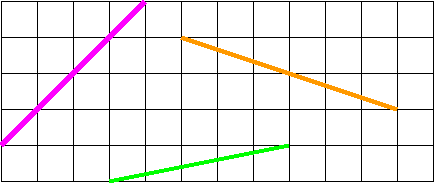
Прямые, которые лежат в одной плоскости и не пересекаются, называются параллельными. Слово «параллельный» в переводе с греческого означает «идущий рядом». Приведите примеры параллельных прямых в окружающей нас обстановке. Начертите параллельные прямые в тетради в клетку.


2 Начертите прямые, параллельные данным.





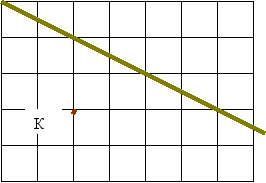
3. Перечертите рисунок в тетрадь. Проведите через точку К прямую, параллельную прямой. Сколько таких прямых можно провести? Сформулируйте вывод.





4. Изобразите параллельные прямые на нелинованной бумаге.


5. Начертите прямую l на нелинованной бумаге, отметьте точки М и К вне этой прямой. Проведите через точки М и К прямые, параллельные прямой l.

6. Начертите треугольник и проведите через каждую вершину прямую, параллельную противоположной стороне. Что замечаете? Запишите вывод. Встречался ли раньше такой рисунок?


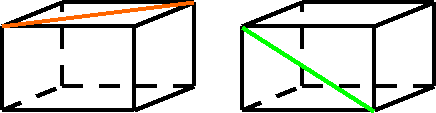
7. На модели прямоугольного параллелепипеда укажите параллельные ребра, грани.

Постройте прямую, параллельную цветной прямой.





8. Как называют четырехугольник, у которого две пары параллельных сторон? Начертите такой четырехугольник в тетради. Обозначьте его АВСД. Назовите все его свойства.





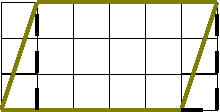
9. Как написать формулу для нахождения периметра, зная длины его сторон а и в? Как найти площадь параллелограмма?


10. Начертите параллелограмм на нелинованной бумаге. Перечислите свойства параллелограмма.


11. Напишите формулы для нахождения площадей фигур:





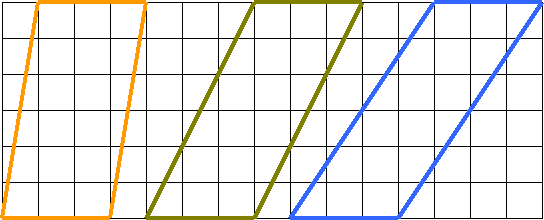
12. Перечертите параллелограммы. Что одинакового и что различного у них?





ЧАСТНЫЕ ВИДЫ ПАРАЛЛЕЛОГРАММА


1. Начертите прямоугольник, ромб, квадрат. Можно ли их назвать параллелограммами?

Перечислите все различия и сходства фигур.

Выводы: а) прямоугольник – это параллелограмм с прямыми углами; б) квадрат – это параллелограмм с прямыми углами и равными сторонами или квадрат – это прямоугольник, у которого все стороны равны, или квадрат – это ромб, у которого углы прямые; в) ромб – это параллелограмм с равными сторонами.


2. Начертите четырехугольник, у которого две противоположные стороны параллельны, а две другие – нет. Как он называется? Вычислить периметр и площадь этой фигуры.

3. Постройте прямоугольник, ромб и квадрат одинаковой площади ,равной 4 см2.

4. Постройте прямоугольник, площадь которого равна 12см2, четырьмя различными способами.

5. Постройте три квадрата, площади которых равны соответственно 8, 9, 10 клеткам.

6. Перечертите четырехугольник, определите его вид. Постройте квадрат, площадь которого равна площади этого четырехугольника.





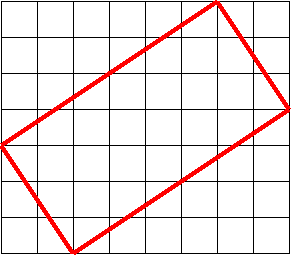
7. Постройте два прямоугольника, имеющие: а) равные периметры и разные площади; б) равные площади и разные периметры.


8. Перечертите 3 ромба, периметры которых равны, а площади равны соответственно 3,4,5 клеткам


9. Постройте прямоугольник. Разбейте его на 2 части, из которых можно сложить остроугольный, прямоугольный и тупоугольный треугольники.

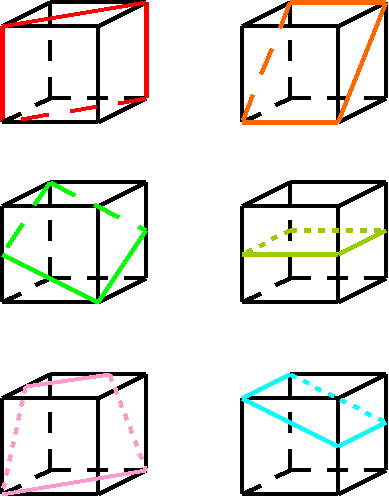
10. Определите вид цветного четырехугольника на каждом рисунке.








КООРДИНАТНАЯ ПРЯМАЯ


1. Рассказ учителя: вспомним Лайнландию, удивительную планету, представляющую собой прямую линию. Отрезки, точки, лучи «живут» на ней. Но как и любые земные жители, лайнланцы ходят друг к другу в гости, возможно пишут письма. А для этого им необходимо знать адреса, где «живет» та или иная точка. На помощь к ним «пришли» числа. Чтобы определить положение точки на прямой по отношению к началу отсчета -–точке О, надо указать расстояние, которое мы задаем сами, выбрав какой-либо единичный отрезок и отложив его последовательно от начала отсчета 1.2,3 и т.д. раз и направление по какую сторону от точки О она находится. Получается шкала.

Н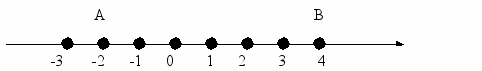о у лайнландцев нет понятий «вправо» и «влево», поэтому они точки шкалы обозначают по-другому: справа от начала отсчета 0 пишут числа 1, 2, 3, ...., а слева числа –1, -2, -3, ...Направление вправо от точки 0 считают положительным и обозначают стрелкой, а влево – отрицательным


Начало отсчета точка 0 изображает число «ноль». Число показывающее положение точки на прямой, называют координатой этой точки. Точка А на рисунке имеет координату -2; точка В - координату 4. Пишут А(-2); В(4). Итак, прямую линию с выбранным на ней началом отсчета, единичным отрезком и направлением называют координатной прямой.


2. Где вы встречались с координатной прямой или ее кусочком – координатным отрезком, лучом?


3. Определите и запишите координаты отмеченных точек





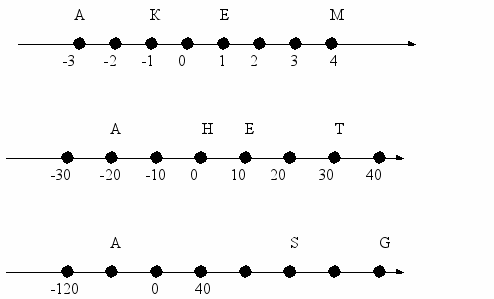
4 .Отметьте точки на координатной прямой а) А(-1), В(-4 )/ С(3)/ Д(2 );

б) К(-20), М(30), N(-15); в) Х(100), F(-200), Z(500)


Назовите три числа, изображения которых на числовой прямой находятся: а) правее А(16 ); б) левее В(-2); в) правее С(4), но левее Д(10); г) правее Е(-7), но левее точки F(1).


Отметьте на координатной прямой точку А(2). Укажите: а) точку В, в которую перейдет точка А при перемещении вправо на 6 единиц; б) точку С, в которую перейдет точка А при перемещении влево на 6 единиц; в) толчку Д, в которую перейдет точка А при перемещении на 7 единиц; г) точку Е, в которую перейдет точка А при перемещении на 7 единиц. Назовите координаты точек В,С,Д,Е.


На сколько единиц переместилась точка Р(4), если после перемещения она попала в точку К(-2)? Если она попала в точку Т(6)?


РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ НА КООРДИНАТНОЙ ПРЯМОЙ


1.





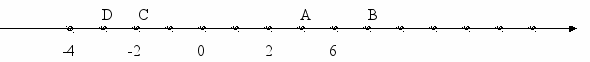
На сколько единичных отрезков удалены друг от друга точки А и В, А и С, А и Д, С и Д, С и В, Д и В? Запишите длины всех отрезков, изображенных на рисунке. Как найти расстояние между двумя точками числовой прямой с помощью вычислений?


2. Найдите длины всех отрезков, концами которых является отмеченные точки, выраженные в единичных отрезках.




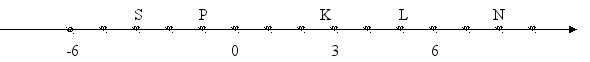
3. Найдите расстояние между К и С. На каком расстоянии точка К находится от точки Е?




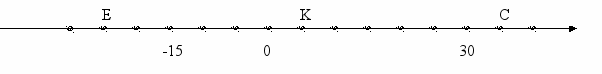
4. Найдите координаты точек и расстояния между ними




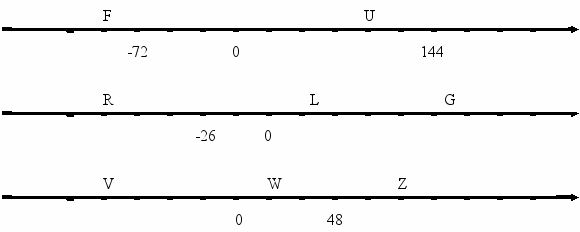
5. Найдите координаты точек и расстояние между ними. Найдите длины всех отрезков с концами в точках К(125), Д(7265), М(-380), N(-230).


6. Отметьте на числовой прямой точки А(8) и В(-6). Точка М – середина отрезка АВ. Найдите координаты точки М. Как можно было найти координаты точки М с помощью вычисления?


7. К(12), N(4) и точка N – середина КС. Найдите координаты точки С.


8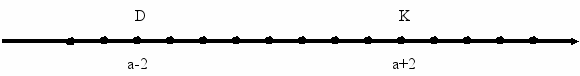. На рисунке показано положение точек К(а+2) и Д(а-2). Отметьте на этом рисунке точку Е(а).


9 .А(6), АВ = 7. Найдите координату точки В.


10. А(-3), АВ = 4, АС=2. Найдите координату точек В и С и длину отрезка ВС.


11. N(-7), Р(5). Отрезок NР переместился вправо на 2 единичных отрезка. Определить новые координаты точек N и Р.


12. Отрезок с концами в точках А(-4), В(1) переместился по прямой так, что точка А стала иметь координату –1. Какую координату стала иметь точка В?


КООРДИНАТНАЯ ПЛОСКОСТЬ


1. Рассказ учителя: Вспомним планету Флатландию. Она представляет собой плоскость. Населяют ее плоские фигуры: многоугольники, углы, отрезки и т.д. Планета бесконечна. Для лучшей ориентации на ней флатландцы «придумали» вот что. Они провели сначала одну ось и расставили на ней числа ..., -3, -2, -1, 0, 1, 2, 3,... Эту ось они назвали осью абсцисс Оx, а затем ей вертикально через точку О(0) провели другую ось и также расставили на ней числа, назвав эту ось - осью ординат Оy. Плоскость, на которой проведены таким образом две оси, называют координатной плоскостью. Изобразите ее.




Положение любой точки плоскости определяется парой чисел. Эту пару чисел называют координатами точки М. Так, например, число 2 называется абсциссой точки М, а число 3 называют ординатой точки М. Обозначают это так М(2;3). При этом всегда на первом месте пишут абсциссу точки, а на втором – ее ординату.

Вспомните, что в нашем мире определяется двумя координатами


2. Постройте точки на координатной плоскости А(2;8), В(3;-4), С(-4;5), Д(-3;7), Е(-5;2), К(8;-1)

3. Отметьте точки а) А(-1;1), В(1;4), С(5;4), Д(3;1); б) К(-2;4), Т(3;3), М(-2;2); в) N(1;-1), S(-1;-4), R(1;-7), Х(3;-4) и соедините их последовательно А,В,С,Д. Расскажите о полученной фигуре.

4. Восстановите рисунок по его коду: (1;7), (-2;4), (-1;4), (-3;2), (-1;-1), (3;-1), (3;2), (5;2), (3;4), (4;3), (1;7).


5. а)Постройте треугольник АВС, если А(1;5), В(3;9), С(9;2);

б) Постройте четырехугольник ДЕFK, если Д(4;2), Е(1;7), F(7;8), К(10;5);

в) Раскрасьте пересечение треугольника АВС и четырехугольника ДЕFK.


6. Постройте точки А(1;4), В(9;10), С(3;9), Д(10;2). Проведите прямые АВ и СД и найдите координаты их точки пересечения М.

а) Постройте прямоугольник АВСД с вершинами А(2;1), В(3;9), С(7;9), Д(7;2) и найдите его Р и S. б) Постройте треугольник МNK с вершинами М(4;1), N(4;8), К(9;1) и найдите S. в) Постройте четырехугольник АДЕF с вершинами А(2;1), Д(2;6), Е(7;6), F(11;1) и найдите его S.


7. Рассмотрите многоугольник на координатной плоскости, обозначьте и запишите координаты его вершин.





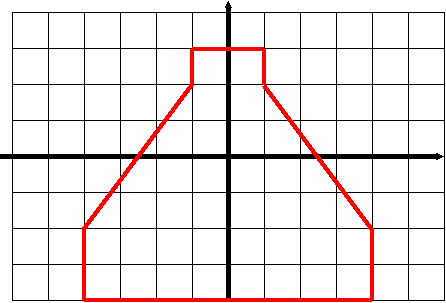
а) Постройте прямоугольник АВСД с вершинами А(2;1), В(3;9), С(7;9), Д(7;2) и найди его Р и S. б) Построй треугольник МNK с вершинами М(4;1), N(4;8), К(9;1) и найди S. в) Постройте четырехугольник АДЕF с вершинами А(2;1), Д(2;6), Е(7;6), F(11;1) и найдите его S.


8. Какие координаты имеет вершина О – пересечение координат осей?


9. Восстановите рисунок по коду: (0;0), (2;6), (4;8), (6;4), (6;0), (2;-2),

(4;-2), (2;-6), (0;-2). Продолжите рисунок, считая ось координат его осью симметрии.


10. Постройте четырехугольник АВСД по координатам его вершин. Если возможно проведите его ось симметрии. Измерьте его площадь..

а) А(-2;2), В(3;2), С(4;-2), Д(-3;-2)

б) А(-2;-2), В(3;0), С(5;-2), Д (3;-4)

в) А(0;4), В(4;6), С(9;6), Д(6;4)

г) А(-3;2), В(1;4), С(5;2), Д(1;0)

д) А(-5;-1), В(-2;2), С(1;-1), Д(-2;-4)

Отметьте на линии точку А с абсциссой 2 и точку В с ординатой 5. Запишите координаты точек А и В.


11. Даны точки А(1, 3), В( -1, 4), С(7, 5), Д(0, 6). Какие из этих точек расположены выше оси абсцисс, левее оси ординат?


12. Постройте четырехугольник АВСД по координатам его вершин А(-8, 6), В(6, 5), С(1, -3), Д(-7, 1).Найдите координаты точки пересечения его диагоналей.


13. В Лайнландии для определения положения точки требуется 1 координата, во Флатландии – две координаты, а в Трехмерии? Сколько осей должно быть в Трехмерии и как они должны располагаться?


УГЛЫ И ДЕЙСТВИЯ С НИМИ


СРАВНЕНИЕ УГЛОВ


1. Рассмотрите рисунок.


Что изображено? Как обозначены углы? Назовите элементы этих фигур. Определите вид углов. Какой из них больше и как это проверить?


2. Вырежьте из бумаги остроугольный треугольник. Как сравнить его углы?


3. Назовите углы на рисунке и сравните их. Определите вид углов.





ИЗМЕРЕНИЕ УГЛОВ


1. На практике не всегда удобно пользоваться способом наложения углов для их сравнения. Действительно, как наложить друг на друга углы, которые образовались при пересечении шоссейных дорог? Чтобы удобно было сравнить углы, их надо научиться измерять. Измерять углы можно разными мерками, но самой распространенной меркой является часть прямого угла. Эту мерку называют градусом и обозначают: 10. Таким образом ,прямой угол равен 900. Острый угол меньше прямого, поэтому его градусная мера меньше 900. Тупой угол больше прямого, значит он больше 900.

2. Известно, что ÐА = 620, ÐВ = 900, ÐС =1510, ÐД = 730, ÐЕ = 1650, ÐК=1160, ÐЕ=30, ÐМ=1480, ÐN=830. Какие из этих углов острые, прямые, тупые.


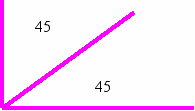
3. На каждом рисунке найдите градусную меру углов, на которых не указана их градусная мера.







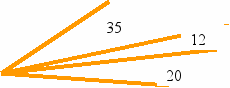
Чтобы измерить угол в градусах, надо узнать, сколько раз в нем содержится 10. Для этого мерку в 1 градус надо последовательно отложить от одной из сторон угла. Измерять углы в градусах непосредственным откладыванием неудобно. Практически углы измеряются с помощью транспортира. Транспортир- это «кривая линейка», на шкале которой зафиксированы результаты откладывания углов от 00 до 1800. Цена деления 10. Чтобы измерить угол с помощью транспортира надо : 1) совместить вершину угла с центром транспортира; 2) расположить транспортир так, чтобы сторона угла проходила через начало отсчета на шкале транспортира; в) найти штрих на шкале, через который проходит вторая сторона угла.


4. Начертите «на глаз»: а) три острых угла; измерьте их и убедитесь, что они получились острыми; б) три прямые угла; в) три тупых угла.


5. Постройте и измерьте угол ВОД, если В(3;5), О(2;2), Д(5;3).


6. Нарисуйте «на глаз» углы в 900, 450, 300. Проверьте свой глазомер с помощью транспортира. Нарисуйте «на глаз» углы в 100, 400, 600, 800. Проверьте себя. Нарисуйте «на глаз» углы в 1200, 1350, 1500. Проверьте себя и вычислите ошибки. б) Начертите 6 разных углов, измерьте их на глаз, затем транспортиром вычислите ошибку глазомера.

ПОСТРОЕНИЕ УГЛОВ


1. Транспортир применяют не только для измерения углов, но и для построения углов. Построим, например, угол ÐСОК = 500. Сначала проведем луч КС, который будем считать стороной искомого угла. Наложим транспортир так, чтобы его центр совпадал с началом луча, а луч КС прошел через начало отсчета шкалы транспортира. Поставим точку Д против штриха с отметкой 500 и проведем луч КД. Мы построили угол ÐСКД в 500, который лежит сверху от прямой КС. Можно построить такой угол и снизу от этой прямой.

2. Постройте угол ÐАОС = 210, ÐКДЕ = 1150, ÐВМР = 860, ÐРLТ = 1750


3. Постройте угол в 700 и проведите с помощью транспортира биссектрису этого угла.

Начертите ÐАОВ = 1200 и разделите его с помощью транспортира лучами ОД и ОЕ на три равных угла


4. Постройте угол ÐНКS = 1100, если К(-4;3), S(-2;-6)


5. Постройте равнобедренный треугольник и измерьте его углы.

ДЕЙСТВИЯ С УГЛАМИ


1. Постройте угол ÐАОС, равный 200 и угол ÐСОВ в 700. Какой угол в результате образовался? Можно ли найти градусную меру этого угла без транспортира? Найдите и сделайте соответствующие записи.

Как складывают углы?

Как вычитаются углы?


2. Вырежьте из бумаги углы в 350 и 800. Постройте в тетради сумму этих углов.

3. Вырежьте из бумаги углы в 1200 и 650. Постройте в тетради разность этих углов.

4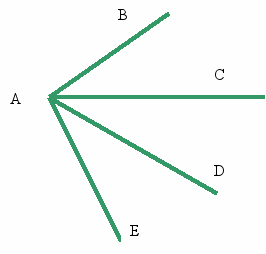. На рисунке ÐВАС = ÐДАВ а) Какие другие углы этого чертежа равны? б) Суммой каких углов является угол ВАЕ? в) разностью каких углов является угол ÐСАД?


5. Вырежьте из бумаги углы в 270, 750, 420. Постройте в тетради сумму этих углов.

6. Вырежьте из бумаги остроугольный, прямоугольный, тупоугольный треугольники. Постройте сумму этих углов каждого треугольника, предварительно «оторвав» их.


7. Что интересного замечаете?





Угол, который вы получили, называется развернутым. Чему равна градусная мера развернутого угла? Запомните: угол, стороны которого образуют прямую, называется развернутым.

Сумма углов треугольника равна 1800


8. Вырежьте из бумаги пятиконечную звезду. Найдите сумму выпуклых 5 ее углов.


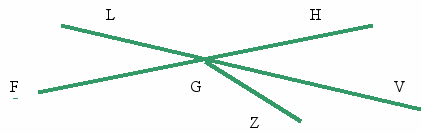
9. Найдите и назовите развернутые углы на рисунке





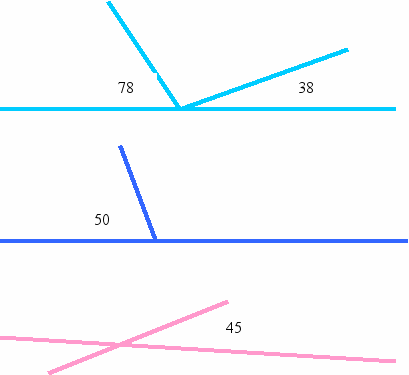
10. Вычислите величины всех углов на рисунках.[.





11. Постройте треугольник АВС, у которого а) ÐА= 640, ÐВ = 900. Вычислите угол С. Проверьте с помощью транспортира. Сравните ваш треугольник с треугольником соседа. Что интересного находите? б) ÐА = 850, АВ = 5 см, АС = 3 см. Сравните ваш треугольник с треугольником соседа. Что можете сказать? В) ÐВ = 380, ÐС = 500, ВС = 4 см. Сравните ваш треугольник с треугольником соседа. Сделайте общий вывод.

Если у треугольников сторона и два , прилежащих к ней угла равны, то треугольники равны.

12. Постройте с помощью циркуля равносторонний треугольник. Догадайтесь, чему равны углы равностороннего треугольника?


13. Постройте квадрат. Проведите в нем диагональ. Найдите градусную меру углов, получившихся треугольников без транспортира.


1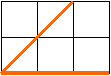3. Перечертите угол в тетрадь. Без транспортира найдите его градусную меру.


14. Треугольник АВС – равнобедренный, с основанием АС. ÐВ = 700. Найдите градусные меры углов А и С.


15. Постройте угол в 640. А теперь без транспортира, а только с помощью линейки, постройте угол в 116. Углы, у которых одна сторона общая, а две другие дополняют друг друга до прямого, называются смежными. Какими свойствами обладают смежные углы?

Сумма смежных углов равна 180


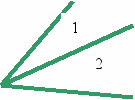
16. Являются ли углы 1 и 2 на рисунке смежными? Почему?













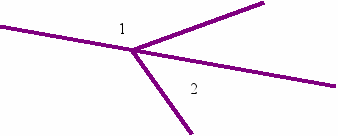
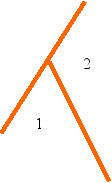
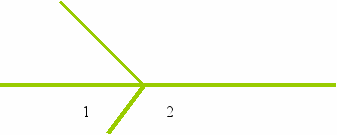
17. Постройте угол в 1540 и нарисуйте угол смежный ему, найдите его величину.

18. Один из смежных углов равен 280. На сколько градусов второй смежный ему угол больше первого?

19. Являются ли смежными ÐАВС = 460 и КМТ = 1340? При каком условии они будут смежными? Могут ли два смежных угла быть: а) острыми, б) прямыми, в) тупыми, г) прямым и острым, д) тупым и прямым, е) тупым и острым.


20. Нарисуйте угол в 750. Без транспортира постройте такой же угол.

Углы, у которых сторона одного дополняет сторону другого до прямого, называются вертикальными. Какими свойствами обладают вертикальные углы.


21. Три пересекающиеся в одной точке прямые делят плоскость на сколько углов? Два угла равны 280 и 360. Чему равны остальные?


22. Вырежьте из бумаги выпуклый и невыпуклый четырехугольники. Найдите сумму углов каждого, путем отрывания углов.


23. Сумма углов четырехугольника равна 3600, или полному углу.

Почему рисунок может служить подтверждением того, что сумма углов четырехугольника равна 3600?





24. Четырехугольник разбивается диагоналями на 2 треугольника, сумма углов в каждом равна 1800, 1800 2 = 3600 Что это доказывает?





25. Поверните ручку вокруг ее конца на 900, еще на 900. На какой угол она повернулась? А теперь поверните ее на 1800. На сколько градусов всего повернулась ручка? Сделай схематичный рисунок.


26. На рисунке найдите сумму указанных углов.





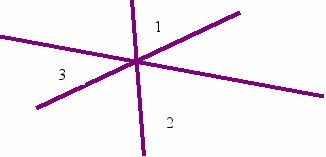
27. Как найти сумму углов пятиугольника, шестиугольника и т.д. не используя транспортир?


28. Нарисуйте треугольник. Продолжите его стороны за вершины (см. рисунок).





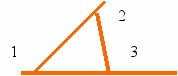
Мы получили внешние углы треугольника. Найдите их сумму. Сделайте вывод.

Сумма внешних углов треугольника, взятых по одному, равна 3600.

Проделайте аналогичную работу с четырехугольником, пятиугольником и т.д.


29.а) Сложите с помощью бумажной полосы правильный пятиугольник. Без транспортира догадайтесь о градусной мере одного угла правильного пятиугольника. б) Изобразите правильный шестиугольник. Догадайтесь: чему равен угол правильного шестиугольника?





30. Представьте себе компас. Какой угол образуют между собой такие направления: а) С и Ю, б) С и СВ, в) В и СЗ, г) ЮВ и СВ.


31. На сколько градусов повернется часовая стрелка за 2 часа, за 5 часов, за 9 часов?

32. Постройте угол, величина которого 2600


33. Постройте смежные углы. Проведите биссектрисы этих углов. Догадайтесь, чему равен угол между биссектрисами смежных углов?


34. Окружность и дуги окружности можно измерять в градусах. Как вы думаете, какую градусную меру имеет окружность? Полуокружность? Начертите дуги в 3600 и 1800 как начертить дуги в 700, 1400 и т.д.? Градусная мера центрального угла соответствует градусной мере дуги, на которую он опирается.


35. Перечертите четырехугольник. Как он называется? Измерьте один угол . Догадайтесь без транспортира о градусных мерах остальных углов.





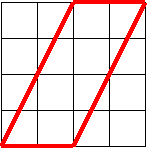
36. На девятиточечном квадрате начертите трапецию, равнобедренный треугольник. Догадайтесь о градусных мерах их углов.


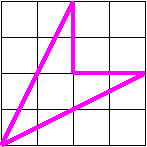
37. Найдите величину вогнутого угла дельтоида:





МНОГОГРАННИКИ И ИХ ЭЛЕМЕНТЫ


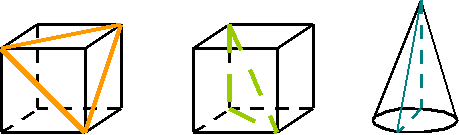
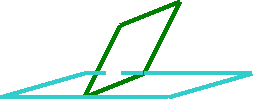
1. В Лайнландии может «жить» угол в 0 градусов, во Фланландии – и другие углы, а в Трехмерни могут «жить» не только плоские углы, но и объемные. Если согнуть лист бумаги, вы получите модель двугранного угла. Линия сгиба называется ребром, а части листа или полуплоскости, называются сторонами или гранями двугранного угла. Обозначим такой угол двумя буквами, поставленными у его ребра. Найдите в классе модели двугранных углов и на геометрических. телах.





2. Сколько двугранных углов у треугольной пирамиды? У куба? Что замечаете?

Количество двугранных углов равно количеству ребер многогранника.


3. Есть ли двугранные углы у конуса? Цилиндра? Почему?


4. Какие двугранные углы считаются равными? Продемонстрируйте с соседом по парте равные двугранные углы с помощью тетради.


5. Двугранные углы могут быть острыми, прямыми, тупыми. С помощью тетради продемонстрируйте модели таких углов

6. С помощью бумажной модели двугранного угла, продемонстрируйте двугранный угол, градусная мера которого 45, 90, 135, 78, 164 градусов.


7. Двугранные углы могут быть вертикальными и смежными. С помощью двугранного угла соседа постройте модели смежных и вертикальных двугранных углов. Сделайте рисунок в тетради.





8. Трехгранным углом называется фигура, составленная из трех плоских углов (см. рис.) Эти углы называются гранями трехгранного угла, а стороны ребрами. Общая вершина плоских углов называется вершиной трехгранного угла. Найдите в окружающей обстановке модели трехгранных углов и на геометрических телах.





9. Аналогично, попробуйте дать определение четырехгранному углу и найти его на геометрических телах.


10. а) вырежьте из бумаги углы в 50, 60, 90, 120, 140, 150 градусов.

б) Изготовьте макет трехгранного угла с плоскими углами: 1) 120, 60. 90 2) 140. 120, 90 3) 150, 90. 60 4) 140, 60. 50 5) 150, 120, 90 6 180. 140, 120.

В каких случаях три угла не могут быть гранями трехгранного угла?


11. Можно ли составить трехгранный угол из плоских углов, сумма которых равна 360.


12. Можно ли составить четырехгранный угол из таких плоских углов а) 40. 70, 100, 150; б) 150. 30, 70, 40?


Многогранником называется тело, ограниченное плоскими многоугольниками. Эти многоугольники называются гранями. Грани многоугольника сходятся в одной точке, образуют многогранный угол. Общие стороны смежных многоугольников называются ребрами.

Выберите многогранник. Посчитайте количество ребер, вершин граней. Какие многогранные углы имеет ваш многогранник. Измерьте плоские углы многогранного угла.


13. В тетрадь выпишите результаты задания № 12 в таблицу

Многогранник	Кол-во ребер	Кол-во граней	Кол-во вершин
Треугольная пирамида	4	4	6
Куб	8	6	12
Четырехугольная пирамида	5	5	8
Восьмигранник .	6	8	13.

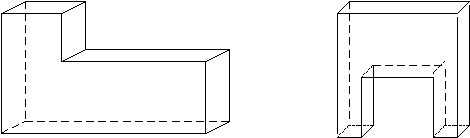
14. Величайший математик Леонард Эйлер (1707-1783) подметил удивительное соотношение: В + Г – Р = 2. Проверьте его, рассмотрев другие многогранники, например такие:





15. Многогранник называется правильным, если все грани -равные правильные многоугольники и все многогранные углы равны. Найдите среди геометрических тел правильные многогранники.

Всего существует правильных многогранников пять. Правильный четырехгранник или тетраэдр. Нарисуйте его в тетрадь и сосчитайте количество граней, вершин, ребер. Какие многогранные углы имеет? Из каких плоских углов состоят трехгранные углы правильного тетраэдра? Измерьте длину ребра и вычислите длину каркаса. Перечертите 1 грань и найдите ее площадь. Найдите площадь всей поверхности правильного тетраэдра. Какой получится многогранник, если считать центры граней правильного тетраэдра за вершины нового многогранника.


16. Рассмотрите правильный восьмигранник, или октаэдр. Нарисуйте его в тетради и сосчитайте количество граней, вершин, ребер. Какие многогранные углы имеет? Из каких плоских углов состоит многогранный угол? Измерьте длину ребра и найдите длину каркаса. Перечертите одну грань и найдите ее площадь. Найдите площадь всей поверхности. Вершинами какого многогранника являются центры октаэдра?


17. Аналогичное задание: рассмотрите правильный двадцатигранник или икосаэдр.

18. Аналогичное задание: рассмотрите шестигранник или куб, или гексаэдр, или правильная призма.


19. Аналогичное задание: рассмотрите правильный двенадцатигранник или додекаэдр.


20. Выпишите в таблицу результаты исследования многогранных углов правильных многогранников.

Многогранник	Плоские углы, составляющие многогранный угол
1. Тетраэдр	60,60,60
2. Октаэдр	60,60,60,60
3. Икосаэдр	60,60,60,60,60,
4. Куб	90.90,90
5. Додекаэдр	108,108,108

Могут ли существовать еще правильные многогранники?


21. Пифагор и его ученики, жившие в Греции до нашей эры, проводили соответствие между правильными многогранниками и четырьмя стихиями : огнем, землей, воздухом, водой, а один многогранник они отождествляли с Вселенной. Постройте это соответствие и обоснуйте его.


Ответ Пифагора: тетраэдр – огонь, куб – Земля, октаэдр – воздух, икосаэдр –вода, додекаэдр – Вселенная. Сравните с вашим ответом.


22. Чему равно наименьшее число красок, которыми можно раскрасить правильный многогранник, если требуется, чтобы две смежные грани были разного цвета.


ОЛИМПИАДЫ ПО ГЕОМЕТРИИ ДЛЯ 3 КЛАССА


1. Разбейте плоскость тремя прямыми на 4 части.


2. Разбейте фигуру, составленную из пяти одинаковых квадратов на 4 равные части.





3. Из 12 спичек сложили прямоугольник и треугольник. Сравните их периметры и площади.







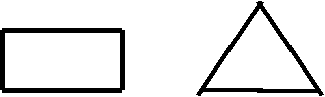
4. Из 10 спичек составлен прямоугольник. Переложите 3 спички так, чтобы площадь уменьшилась на 2 «квадратные» спички.





5. Из 12 спичек составьте фигуру, площадь которой равна 9 «квадратным» спичкам.


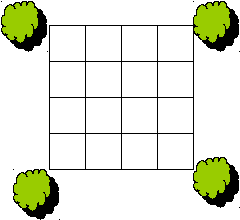
6. Имеется квадратный пруд, по углам которого растут 4 дуба. Расширьте пруд так, чтобы он сохранил квадратную форму, но площадь увеличилась в 2 раза. И чтобы все дубы остались на своих местах, но у берегов нового пруда.





ЛИТЕРАТУРА

1. Зайкин М.И. Развивай геометрическую интуицию. – М.: Просвешение, 1995.

2. Звонкин А.К. Малыши и математика. Домашний кружок для дошкольников. – М.: Московский центр непрерывного образования, 2007.

3. Давыдов В.В., Горбов С.Ф.,.Микулина Г.Г, Савельева О.В. Математика. 1 класс. – М.: МИРОС, 1995.

4. Протасов В.Ю., Шарыгин И.Ф. Геометрия. Рабочая тетрадь к учебнику Шарыгина И.Ф. «Геометрия 7-9». – М.: Дрофа, 1997.

5. Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия. – М.: МИРОС, 1992.

6. Шарыгин И.Ф. Геометрия 7. Теория и задачи. – М.: МИРОС, 1995.

Эбботт Э. Флатландия. – М.: Мир,1976.