Российская академия образования Институт научной информации и мониторинга
| Вид материала | Документы |
- Доклад на Всероссийской научной конференции «От СССР к рф: 20 лет итоги и уроки», 140.15kb.
- Из истории российского образования, 1157.84kb.
- Управление образованием, 733.04kb.
- Государственная академия наук российская академия образования институт семьи и воспитания, 5970.09kb.
- Государственная академия наук российская академия образования институт семьи и воспитания, 2933.75kb.
- Государственная академия наук российская академия образования институт семьи и воспитания, 3113.4kb.
- Государственная академия наук российская академия образования институт семьи и воспитания, 3011.43kb.
- Государственная академия наук российская академия образования институт семьи и воспитания, 4091.81kb.
- Государственная академия наук российская академия образования институт семьи и воспитания, 3731.34kb.
- Ханнанов Наиль Кутдусович, Институт научной информации и мониторинга рао, e-mail: khann@dio, 244.27kb.
Приложение 1. Самохина С.Л. Развитие продуктивной творческой деятельности младших школьников .
Методические рекомендации.
ПУТЕШЕСТВИЕ НА ПЛАНЕТУ ФЛАТЛАНДИЯ ИЛИ ПЛОСКОСТЬ
1. Вот как описывает этот мир в своей книге Эдвин Э.Эбботт: «…Представьте себе огромный лист бумаги, на котором отрезки прямых, Треугольники, Квадраты, Пятиугольники, Шестиугольники и другие фигуры, вместо того, чтобы неподвижно оставаться на своих местах, свободно перемещаются по всем направлениям вдоль поверхности, не будучи, однако, в силах ни приподняться над ней, ни опуститься под нее, подобно теням (только твердым и со светящимися краями), и вы получите весьма точное представление о моей стране и моих соотечественниках…» Оказывается, если ваш тетрадный лист бесконечно продолжить, то вы можете представить себе Флатландию, что означает - плоскость. Какие еще поверхности могут служить моделями плоскости
На каких предметах есть плоские поверхности?
2. На альбомном листе, который служит также моделью Флатландии, нарисуйте жителей Флатландии. Они имеют свои имена-обозначения. Как вы думаете, как обозначается треугольник? Тремя заглавными буквами, которые пишут около вершин треугольника. Аналогично обозначаются другие многоугольники. Но не надо забывать, что читать имя многоугольника надо строго последовательно называя буквы, начиная с любой. Например, четырехугольник можно назвать АВСД или ВСДА или ДСВА, но
нельзя называть так АСДВ.
Но жителей так много, что, кажется, не хватит букв для их обозначения. Тогда флатландцы придумали хитрость: можно в обозначении использовать одну букву, но ставить возле нее число. Например, треугольник М1 М2 М3. Как думаете, теперь хватит букв?
3. Рассмотрите рисунок:
Может ли такая фигура жить во Флатландии? Из чего состоит эта фигура? Поставьте ладони на стороны этой фигуры. Как называется эта фигура? Точку, из которой выходят лучи, называют вершиной угла, а лучи - сторонами. Угол может быть прямым, покажите его ладонями.
4. Начертите прямые углы в тетради.
Для обозначения углов используют три буквы или одну, вершину. Например, угол АВС или угол СВА или угол В. Будет ли угол ,начерченный на доске, прямым? Как это проверить?
5. Начертите в тетради несколько острых углов и каждому дайте имя.
Можно ли начертить угол больше прямого? Начертите и обозначьте его. Углы, больше прямых, называют тупыми.
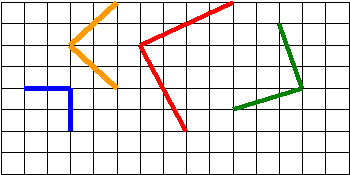
6. Начертим ломаную: 3 клетки вниз, 4 клетки вправо и т.д.
Может ли ломаная быть жительницей Флатландии? Как ее обозначить? Что интересного можно рассказать об этой ломаной?
Назовите углы по буквам тремя способами. Какие это углы?
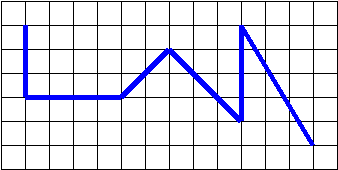
7. Постройте ломаную, звенья которой образуют только а) прямые углы,
б) острые углы, в) тупые углы.
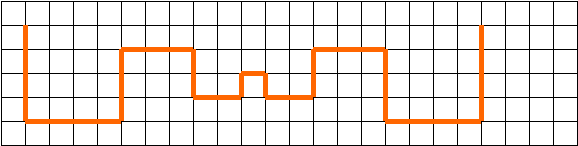
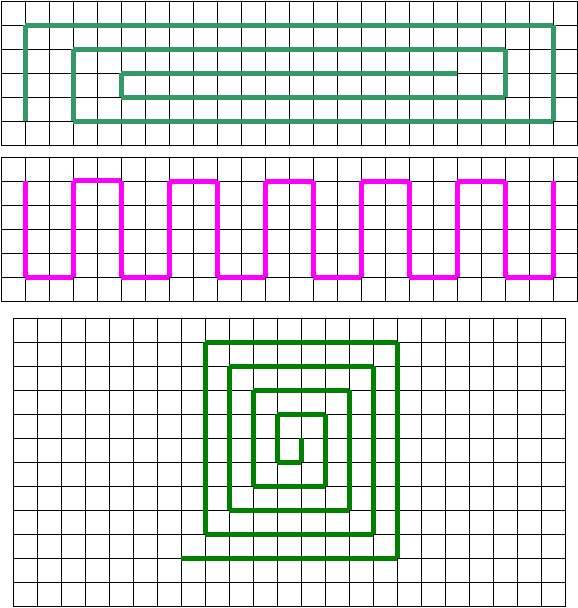
8. Рассмотрите рисунок:
Сколько углов вы видите? Назовите их. Какие они по виду
9. Начертите на нелинованной бумаге прямой угол АВС. Здесь же начертите острый ДВС .
Возможны два варианта:
Какой угол образовался? Какой он по виду?
10. В виде чего видят друг друга флатландцы? Положим треугольник на поверхность стола. «Каким вы увидите его, если посмотрите на него сверху, показано на рисунке а, каким он предстанет перед вами, если луч вашего зрения будет все более приближаться к поверхности стола, не совпадая с нею полностью, видно из рисунков б и в. Есть и же угол вашего зрения сольется с поверхностью стола (именно так и смотрят друг на друга флатландцы), то увидите ничего, кроме прямолинейного отрезка г.» Так описывает автор книги «Флатландия» Э.Эбботт.
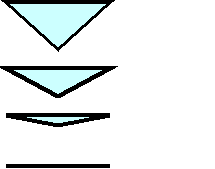
«…Наши моряки испытывают нечто подобное, когда, странствуя по морям, открывают остров или землю, лежащие у самого горизонта. Еле видимый берег может быть изрезан бухтами, мысами, может иметь сколько угодно выступов и впадин любой протяженности, тем не менее с большого расстояния вы не увидите ничего, кроме сплошной серой линии на поверхности воды». Во Флатландии многие фигуры видятся в виде отрезков, которые увеличиваются, если фигуры приближаются, или уменьшаются, если- удаляются. Независимо от того, имеет ли флатландец форму треугольника, квадрата, пятиугольника, окружности, его всегда увидят в виде отрезка. Но каких жителей можно увидеть не в виде отрезка?
Правильные фигуры или уважаемые жители Флатландии
1. Э.Эбботт рассказывает о жителях Флатландии: «…Средние слои общества во Флатдандии образуют Равносторонние Треугольники. Лица, владеющие какой-либо профессией, и джентльмены имеют форму Квадратов и Пятиугольников. Затем идут благородные сословия. Когда число сторон многоугольника становится столь велико, а их длина столь мала, что фигуру нельзя отличить от окружности, ее включают в Круговой орден.» Королевой является Окружность. Чем больше в фигуре равного, тем более она уважаема среди своих соотечественников. А если все стороны равны и углы равны, то ее удостаивают звания Правильной фигуры.
2. Как построить Правильный треугольник, т.е. треугольник, у которого все стороны и углы равны? С помощью циркуля.
Строим окружность радиусом 2см и центром в точке А. Берем на окружности точку В и проводим окружность такого же радиуса с центром в точке В. Получились две точки в пересечении. Одну из них обозначим точкой С. Где же правильный треугольник? Это треугольник АВС.)
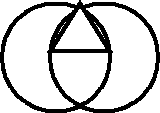
Чему равна длина стороны этого треугольника? Как убедиться в том, что у него углы равны?
Чем интересен правильный треугольник? Какого вида у него углы? Сколько осей симметрии имеет правильный треугольник?
3. Правильный четырехугольник, т.е. четырехугольник, у которого стороны и углы равны, называют квадратом. Начертите его на нелинованном листе. Какие углы у квадрата?
4. Можно ли квадрат начертить с помощью циркуля?
Начертите окружность и проведите ее диаметр АВ. С помощью угольника постройте прямой угол с вершиной в центре окружности. Продолжите его сторону. Получаем второй диаметр, который образует с первым 4 прямых угла. Где же квадрат?
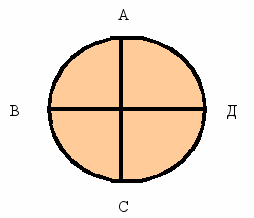
Надо соединить точки А, В, С, Д. Назовите полученный квадрат и убедитесь в том, что это действительно квадрат. Покажите равные дуги на окружности
5. Правильный пятиугольник построить пока нам будет трудновато. Есть замечательный способ-складывание его из полоски бумаги. Учитель раздает каждому по полоске шириной 3см и длиной 20см. Завязываем узел.
6. Правильный шестиугольник, т.е. шестиугольник, у которого все стороны и углы равны, построить легко. Чертим окружность и 6 раз укладываем радиус.
7. У правильного треугольника все три угла острые, у квадрата все прямые, у правильного пятиугольника все углы тупые, у правильного шестиугольника тоже все углы тупые. Как вы думаете, какие углы будут у правильных 7-8-9-угольников? Что происходит с углами правильных многоугольников по мере увеличения их сторон?
Замащивание плоскости одинаковыми многоугольниками
1.Однажды флатландцы решили украсить свою планету: покрыть ее одинаковыми фигурами, без пробелов. Как решили эту задачу правильные треугольники?
Для этого вырежьте из бумаги одинаковые правильный треугольники и наклейте их на лист бумаги без пробелов.
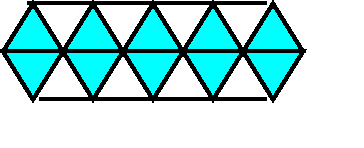
Смогут ли правильные треугольники украсить всю Флатландию?
2.Под силу ли квадратам заполнить планету?
3.Могут ли правильные пятиугольники украсить Флатландию?
4. Могут ли правильные шестиугольники решить задачу об украшении Флатландии? Для этого нам понадобятся одинаковые правильные шестиугольники. О чем надо договориться, чтобы у всех получались одинаковые шестиугольники?
Путешествие по городам Флатландии
Прямоград
1. Во Флатландии есть замечательные города. В одном сегодня мы побываем. Его название-Прямоград. Все улицы в этом городе пересекаются под прямым углом. О таких улицах говорят, что они расположены перпендикулярно друг другу. А живут там жители, у которых есть прямые углы. Прямоугольник является мэром этого города. Нарисуйте его и расскажите о нем. Будем записывать подмеченные вами свойства прямоугольника столбиком. С чего начать знакомство? С имени.
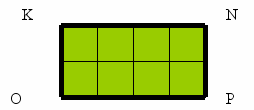
Геометрический характеристика прямоугольника
1.КNРО-прямоугольник
2.NK=РО=2см, NР=КО=2см5мм
3.Р=9см
4.S=5кв.см.
5.Имеет 2 оси симметрии
6.NО=КР
7.Все углы прямые
2. Будут ли данные четырехугольники прямоугольниками
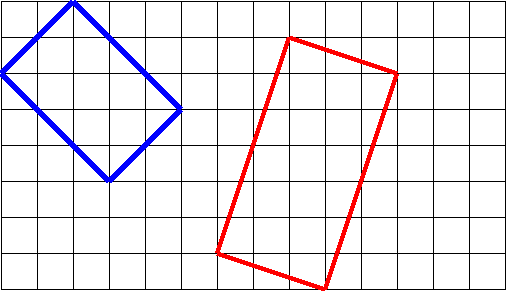
3. Померьте площадь данных фигур, разрезав и переложив так кусочки, чтбы легко можно было посчитать количество клеток.
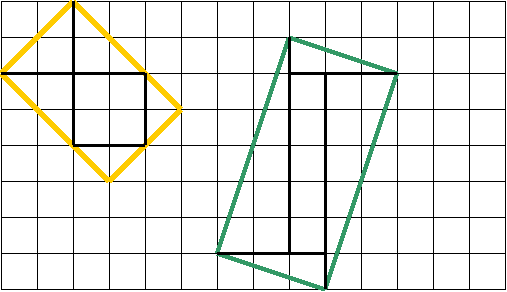
Попробуйте нарисовать другие прямоугольники.
4. Можно ли замостить одинаковыми прямоугольниками плоскость? Попробуйте.
5. Квадрат тоже является жителем Прямограда, он - заместитель прямоугольника. Его тоже называют прямоугольником, т.к. все углы у него прямые. Давайте начертим его, обозначим и также составим геометрический рассказ о нем, вспомнив его свойства.
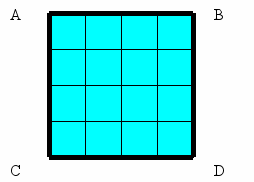
Геометрическая характеристика квадрата
1.АВСД-квадрат
2.Имеет 4 оси симметрии
3.АВ=ВС=СД=АД=2см
4.Р=2.4=8см
5.S=4кв.см
6.Можно замостить плоскость (это уже проделывали)
7.Все углы прямые
8.АС=ВД
А
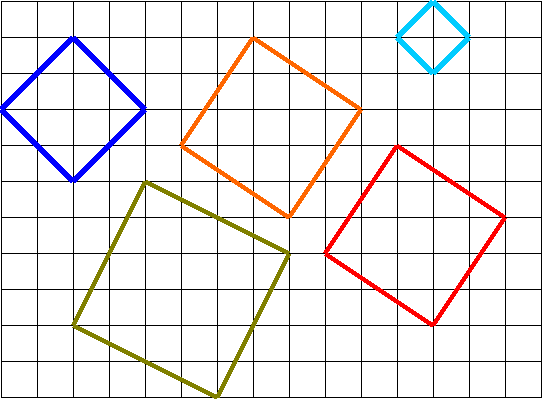если квадрат нарисовать иначе, то как померить его площадь? Вспоминаем способ перекроя:6. Квадрат решил катиться по Флатландии вдоль прямой.
Попробуйте нарисовать след, который оставить верхняя левая вершина., центр квадрата?
7. Два одинаковых квадрата расположились на плоскости несколькими способами так:
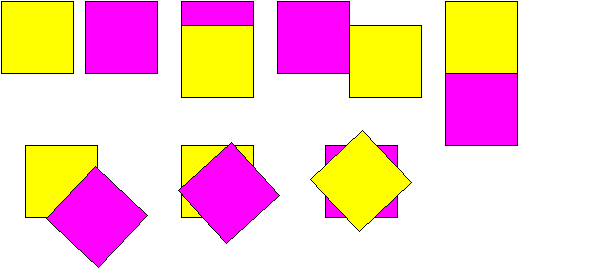
Как еще могут располагаться эти квадраты? Какие при этом фигуры они образуют? Нарисуйте разное расположение одинаковых прямоугольников на плоскости.
8. Квадрат разрезали на две части. Можно ли из этих частей сложить треугольник?
Как надо разрезать квадрат на две части, чтобы из них можно было составить прямоугольник, четырехугольники и другие фигуры?
9. Попробуйте начертить четырехугольник с двумя прямыми углами. Обозначьте его и напишите его свойства.
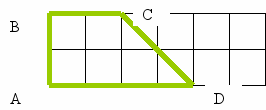
Геометрическая характеристика
1.АВСД-четырехугольник (трапеция)
2.<А=<В-прямые,
3.Нет оси симметрии
4.АВ=2см, ВС=1см, АД=3см, СД=3см6мм
5.Р=9см6мм
6.S=3кв.см
7. Можно замостить плоскость.
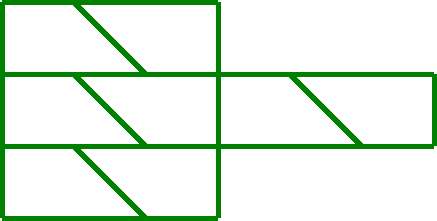
Можно ли замостить трапециями плоскость, укладывая их таким образом?
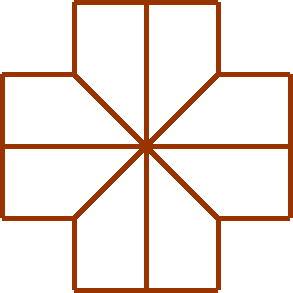
Что интересного подмечаете?
10. Попробуйте фигуру, подобную данной, разбить на маленькие.
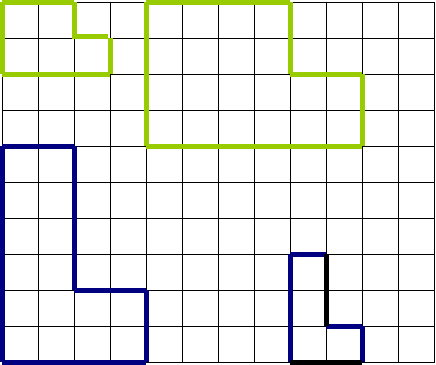
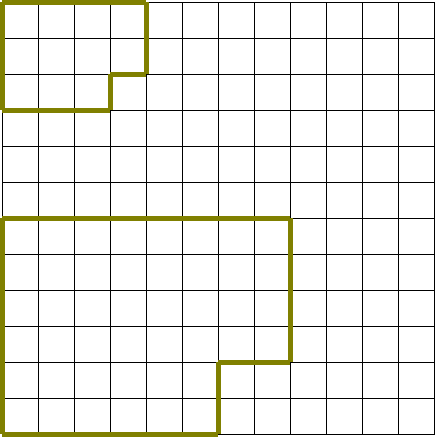
Дайте геометрические характеристики этих фигур.
11. Есть ли у этой фигуры прямые углы. Дайте ей геометрическую характеристику
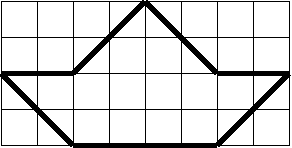
Можно ли замостить ею плоскость, укладывая их таким образом?
12. В Прямограде живут фигуры, у которых есть прямые углы. Какие четырехугольники могут быть жителями Прямограда? Попробуйте провести исследовательскую работу. Сначала начертите четырехугольник с одним прямым углом.
Дайте ему геометрическую характеристику.
П
опытайтесь замостить им плоскость.13. Нарисуйте четырехугольник с двумя прямыми углами, с тремя прямыми углами. Дайте им геометрические характеристики.
Сколько прямых углов может быть у пятиугольника, шестиугольника?. Попробуйте их нарисовать.
14. Перерисуйте этот восьмиугольник, дайте ему геометрическую характеристику. Может ли он являться жителем Прямограда?
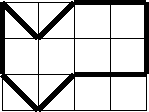
15.Можно вспомнить фигурки пентамино или гексамино, как жителей Прямограда и исследовать их.
Параллелоград
16. Сегодня мы посетим город, мэром которого является фигура, изображенная на рисунке. Перерисуйте ее. Дайте ей имя и напишите ее свойства.
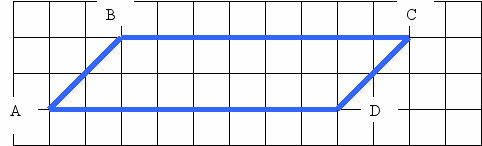
2.
3.АВ=СД=2см8мм, ВС=АД=3см
4.Р=11см6мм
5.S=6кв.см
6.Нет осей симметрии
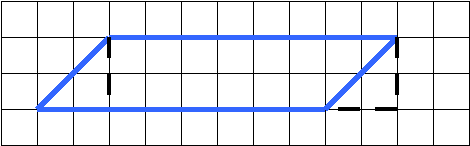
17.Если продолжить укладку одинаковыми параллелограммами, то получится ли замостить всю плоскость?:
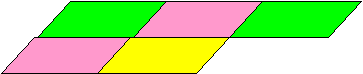
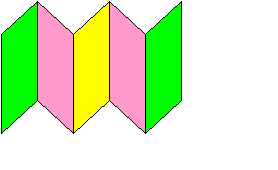
Попробуйте найти другие способы замащивания плоскости одинаковыми параллелограммами.
Если продолжить противоположные стороны этого четырехугольника, то будут ли они пересекаться? Как называются такие прямые? (Параллельные). Отрезки, лежащие на параллельных прямых называют тоже параллельными. Поэтому стороны АВ и СД-параллельные стороны, ВС и АД-тоже параллельные. Вместо слова «параллельные» пишут знак //. Запишем АВ//СД и ВС//АД.
А четырехугольник, у которого противоположные стороны попарно параллельны, называют параллелограммом. Постройте параллелограммы других размеров.
18.Построим четырехугольник: отметьте точку, от которой вправо и влево отступите по 1 клетке, а вниз и вверх по 4 клетке. Как называется этот четырехугольник?
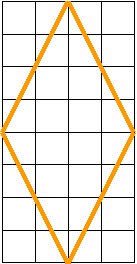
У этого четырехугольника есть и другое название-ромб. Напишите его свойства. Постройте ромбы других размеров.
19.Найдите в окружающей обстановке модели параллельных линий.
20.Перерисуйте фигуру. Будет ли она жителем Параллелограда, т.е. есть ли у нее параллельные стороны? Напишите ее свойства.
21.Есть четырехугольник, у которого только две стороны параллельны, а другие нет. Начертите его. Он называется трапецией.
22. Придумайте жителя Параллелограда и напишите его свойства.
23. Обозначьте ломаную и назовите параллельные ее звенья.
24. Найдите лишнюю:
25. Кто защищает жителей Флатландии? «…Наши солдаты…имеют форму Треугольников с двумя равными сторонами, каждая из которых имеет в длину около 11 дюймов, и основанием, или третьей стороной, столь короткой ( длина основания нередко не превышает половины дюйма), что углы при вершине этих Треугольников необычайно остры и имеют устрашающий вид. …Треугольники с двумя равными сторонами…принято называть Равнобедренными.» Так описывает солдат Флатландии Э.Э.Эбботт.
Начертите равнобедренный треугольник на нелинованном листе бумаги.
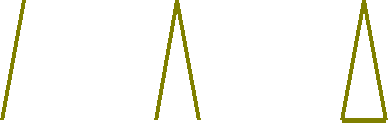
Обозначьте его. Какие стороны равны? Третья сторона, не равная двум данным, называется основанием. Какие углы получились у вашего равнобедренного треугольника? Попробуйте начертить равнобедренный треугольник с прямым углом. С чего начать?
Попробуйте начертить равнобедренный треугольник с тупым углом.
26 .Нарисуйте все равнобедренный треугольники с вершинами в отмеченных точках.?
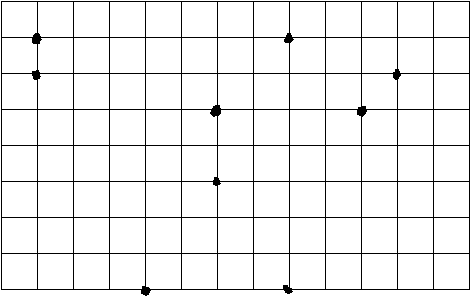
Изображенный отрезок является: а) боковой стороной, б) основанием равнобедренного треугольника. Нарисуйте все равнобедренные треугольники, вершины которых находятся в узлах клетчатой бумаги.
27. Перечертите равнобедренный треугольник и напишите его геометрическую характеристику.
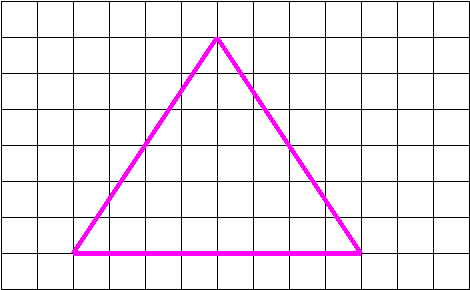
28. Начертите квадрат АВСД и проведите в нем диагонали. Сколько равнобедренных треугольников насчитаете?
29. Рассмотрите рисунок из пяти одинаковых квадратов Что можно сказать о треугольнике?
30. Будет ли правильный треугольник равнобедренным?
КРИВОГРАД
1.Во Флатландии королевой является Окружность - криволинейная фигура. Могут ли жить другие криволинейные фигуры во Флатландии? Перерисуйте фигуру. Обозначьте ее. Напишите ее свойства.
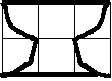
1.АВ=ЕД=1см5мм, АО=СВ=ЕО=СД
2.Имеет 1 ось симметрии
3.S=1кв.см
4.Можно замостить плоскость:
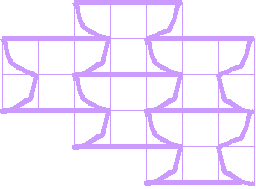
2.Какая фигура получается вырезанием из листа бумаги по окружности? (Круг.) Можно ли кругами замостить плоскость? Если к каждому кругу соответствующим образом «добавить» один такой пробел, то, на первый взгляд, становится возможным покрыть плоскость такими кругами, снабженными каждым одним острием.
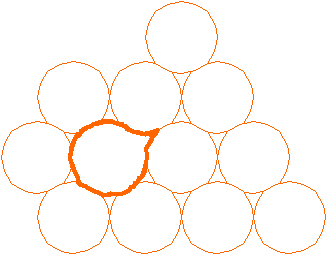
3.Попробуйте теперь осуществить покрытие, выбрав в качестве основной фигуры:
а) круг, на который насажены два смежных «треугольных пробела»
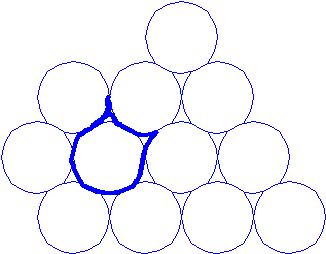
б
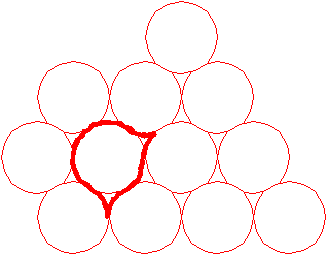) круг, на который эти два «треугольника» насажены так, что между ними один такой «треугольник» пропущенв) круг с двумя диаметрально-противоположно-насаженными «треугольниками»
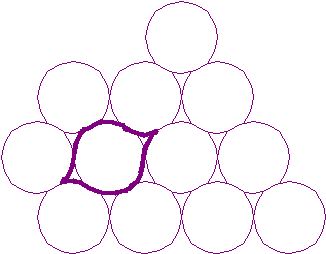
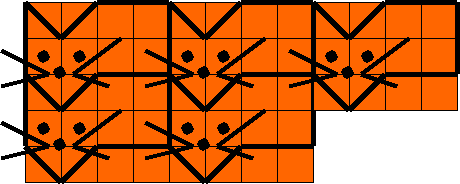
Полученные работы можно раскрасить в виде головок животных или чего-то другого.
4.Можно ли замостить плоскость кругами с тремя «треугольниками»?
РАСПОЛОЖЕНИЕ ФЛАТЛАНДЦЕВ И ИХ ПЕРЕМЕЩЕНИЕ
1.Точка А отправилась в путешествие по Флатландии. Изобразите ее путешествие: сначала она передвинулась на 5см вправо, затем на 2см5мм вниз, на 3см вправо, на 1см5мм вверх, на 7см влево. Начертите линию пути, которую образовала точка в результате своего пути, «след на песке». Как называется это линия? Что можете о ней рассказать?
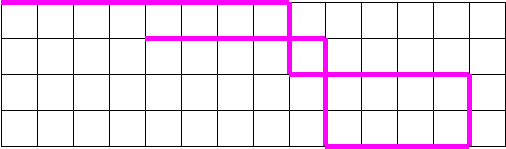
2.Расскажите о движении точки .
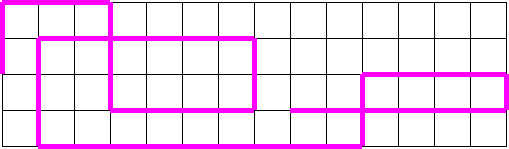
3.Отрезок ВС длиной 1см5мм отправился в путешествие по Флатландии:2см вправо, затем 2см5мм вправо, 2см 5мм вниз, 1см5мм вправо. Изобразите его передвижение и закрасьте его «след на песке». Как выглядит «след» отрезка?
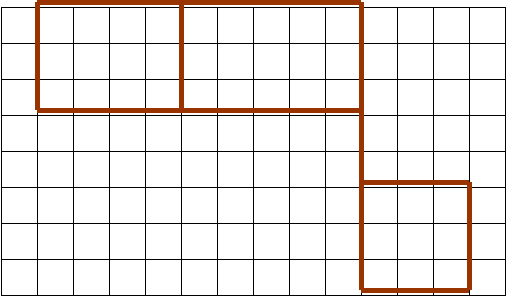
Что можете рассказать о прямоугольнике и квадрате?
4.Расскажите о путешествии отрезка , перерисуйте его передвижение и закрасьте «след», оставляемый им.
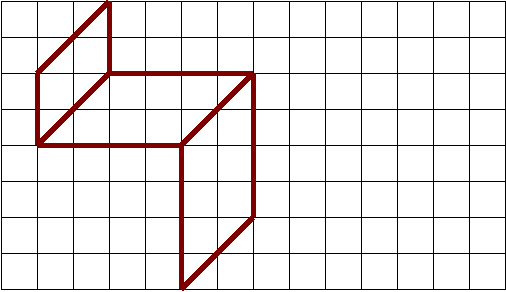
Какая получилась фигура? Как она называется? Перечислите ее свойства.
5.Можно замостить плоскость этой фигурой?
Можно раскрасить получившийся паркет, т.к. рисунок напоминает уток.
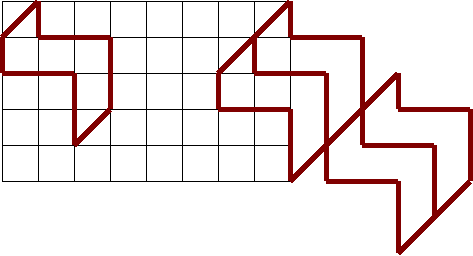
6.а) Какая фигура будет «заметаться», если отрезок ОР будет вращаться вокруг точки О? Нарисуйте эту фигуру. Как при этом называется точка О и отрезок ОР Какой след останется в результате вращения отрезка ОР вокруг своей середины?
б) Нарисуйте горизонтально отрезок ДС, поверните его вокруг точки С так, чтобы он перешел в вертикальное положение. Какая фигура при этом будет им «заметаться»?
7. Отрезок длиной 1см сначала передвинулся на 3см вниз, потом на 1см вправо, на 1см вверх, на 1см вправо, на 1см вниз, на 3см вверх, на 1см влево, на 1см вниз. Заштрихуйте полученную фигуру. Расскажите устно свойства данной фигуры.
8.Начертите окружность с центром в точке А и радиусом 1см5мм. Нарисуйте ее путешествие: 3см вправо, 1см5мм вниз, 1см вправо, 2см вверх
9.Рассмотрите рисунок:
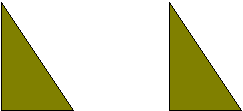
Покажите, на какое расстояние передвинулся треугольник.
10. Мог ли треугольник (1) в результате движения на плоскости принять положение треугольника (2)?
11. Каким образом невыпуклый шестиугольник (1) занял положение (2)?
12. Как могут располагаться жители во Флатландии? Рассмотрите рисунки расположения двух одинаковых треугольников и самостоятельно ответьте на поставленный вопрос.
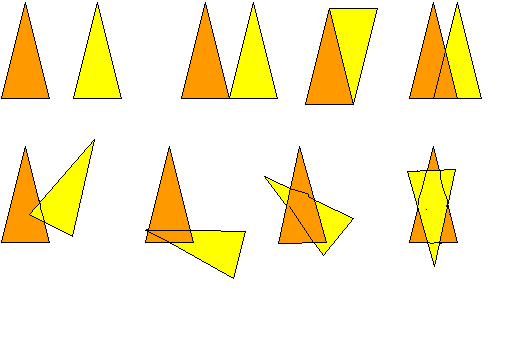
13. Нарисуйте расположение двух одинаковых прямоугольников, чтобы в пересечении образовался: а)квадрат, б) треугольник, в) пятиугольник.
14. Как надо расположить два одинаковых треугольника, чтобы в пересечении образовался квадрат.
ТРЕХМЕРИЯ ИЛИ ПРОСТРАНСТВО, В КОТОРОМ МЫ ЖИВЕМ
ЗНАКОМСТВО С ТРЕХМЕРИЕЙ И ЕЕ ЖИТЕЛЯМИ
1 .Как-то в одной семье флатландцев, между дедушкой Квадратом и маленьким, но очень способным, внуком Шестиугольником состоялся разговор. Дедушка «…показал внуку, что Точка, пройдя прямолинейный путь длиной в 3 дюйма, описывает Отрезок прямой длины в 3 дюйма, которому можно сопоставить число 3. Отрезок длиной в 3 дюйма, перемещаясь на 3 дюйма (и оставаясь при этом параллельным своему начальному положению, и двигаясь в таком направлении, чтобы ни одна Точка отрезка не занимала положения, которое ранее занимала другая Точка отрезка), порождает Квадрат со стороной в 3 дюйма, которому можно сопоставить произведение 3.3.» Этот рассказ можно сопроводить рисунком:
Внук внимательно слушал дедушку и внезапно воскликнул: «Пусть будет по-твоему….Тогда и квадрат со стороной в 3 дюйма, двигаясь каким-то образом параллельно самому себе, причем ни одна точка квадрата не должна при движении занимать положения, которое занимала другая его Точка ( хотя я не могу представить себе, как происходит это движение), должен описывать нечто ( хотя я не понимаю, что это за фигура),имеющее вдоль каждого измерения по 3 дюйма. Этому нечто мы должны сопоставить произведение 3.3.3.» Как должен двигаться квадрат? Какая фигура при этом образуется? Что означает число, равное 3.3.3?
Почему Шестиугольник не мог назвать это тело?
2. Когда внук Шестиугольник ушел спать, дедушка Квадрат «воскликнул:-Мальчишка просто глуп! В тот же миг он почувствовал, что в комнате кто-то есть, и даже ощутил озноб от пронизывающе холодного дыхания незнакомца. …Чей-то голос отчетливо произнес:-Мальчик вовсе не глуп, и произведение 3.3.3 имеет очевидный геометрический смысл.»Каков был ужас Квадрата, когда прямо перед собой он увидел фигуру. Он подумал, что это Окружность, но таинственная фигура на его глазах меняла свои размеры. Через некоторое время гостья снова заговорила:»-В известном смысле меня действительно модно считать Окружностью, причем более совершенной, чем любая другая Окружность во всей Флатландии. Однако, я представляю собой множество Окружностей,образующих единое целое. …
Квадрат. Откуда вы прибыли?
Гость. Из Пространства.
Квадрат. Ваша светлость, но разве вы не находитесь в Пространстве в данный момент?
Гость. А что вы знаете о Пространстве?
Квадрат. Пространство, ваша светлость, -это длина и ширина, продолженные до бесконечности.
Гость. …Вы мыслите только в двумерном пространстве. Я же прибыл, дабы возвестить вам о трехмерном пространстве: ширине, длине и высоте… .Вы живете на Плоскости. То, что вы называете Флатландией, как бы представляет собой огромную поверхность некой жидкости. Вы и ваши соотечественники передвигаетесь, «плаваете» по этой поверхности, не имея возможности ни приподняться над ней, ни опуститься под нее. Я не плоская фигура, а объемное тело. …Пересекаясь с вашей Плоскостью, я образую в сечении … окружность. Ибо даже Сфера (так называют меня обитатели страны, в которой я живу), если у нее возникает необходимость предстать перед обитателями Флатландиии, вынуждена принимать форму Окружности.» Квадрат вспомнил, как он летал в Лайнландию, в которой умещался лишь небольшой срез, или сечение - отрезок.
«Гость. Точно так же в вашей стране двух измерений мне не хватает места, поскольку я-существо трехмерное. Лишь небольшой срез, или сечение, моего тела умещается во Флатландии. Его-то вы называете Окружностью. …За один раз вы можете видеть лишь одно из моих сечений или окружностей, поскольку не в состоянии оторвать свой взгляд от плоскости Флатландии. Но вы можете увидеть, как уменьшаются размеры моего сечения, когда я возношусь в Пространство. Смотрите же –я поднимаюсь. Вы увидите, как моя Окружность будет уменьшаться в размерах до тех пор, пока не стянется в точку и полностью не исчезнет. Квадрат как не напрягал свое зрение, никакого «подъема» ему увидеть так и не удалось, но «незнакомец» действительно стал уменьшатся в размерах, пока совсем не исчез. …Из глубин Ниоткуда до Квадрата донесся низкий голос: «Я полностью вышел из флатландии? Теперь вы убедились? Смотрите внимательно: я медленно возвращаюсь во Флатландию, и вы увидите, как мое сечение будет постепенно увеличиваться?
3. Итак, сфера, шар, куб-это жители Трехмерии, т.к. у них есть длина, ширина и высота. Покажите эти величины у этих фигур. Какие еще фигуры живут в Трехмерии?
Покажите их длину, ширину, высоту.
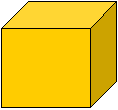4. Как обозначаются трехмерцы? Назовите переднюю грань, заднюю, боковые грани.
5. Начертите прямоугольный параллелепипед. Обозначьте. Назовите равные между собой грани.
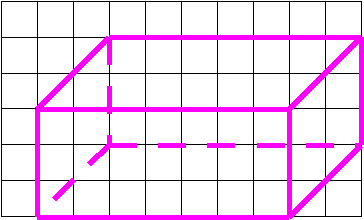
Какие тела можно из них составить так, чтобы они были «склеены» гранями? Как называется это? Сколько у него граней, вершин, ребер? Покажите три его измерения.
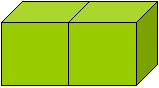
6. Аналогичное задание с тремя одинаковыми кубиками.
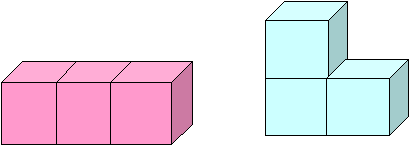
ПУТЕШЕСТВИЕ ГЕОМЕТРИЧЕСКИХ ТЕЛ ВО ФЛАТЛАНДИЮ
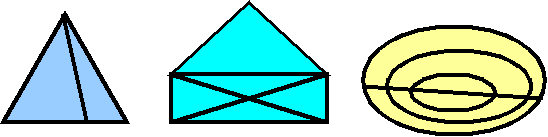
1. После того, как Сфера побывала во Флатландии рассказала об этом своим соотечественникам, то Конус тоже захотел увидеть эту планету. В виде чего флатландцы его увидят?
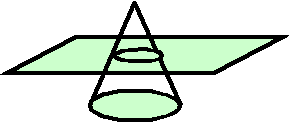
Парабола-часто встречающаяся линия: когда мы бросаем предмет, то он летит по параболе. Кометы могут двигаться по эллипсам,параболам или гиперболам. Дети могут делать рисунки. Окружность, эллипс, треугольник и т.д.-это фигуры, которые образуются в результате пересечения плоскости и конуса. (Поэтому их называют сечениями конуса.)
2. Рассмотрите:конус, куб, прямоугольный параллелепипед, пирамида, цилиндр.
Какое тело из данных оставило такие следы во Флатландии?Докажите,что это цилиндр.
Какой еще след мог оставить цилиндр? Как он должен был «прифлатландиться»? Итак, что является сечениями цилиндра и плоскости?
3. Какие фигуры являются сечениями куба?
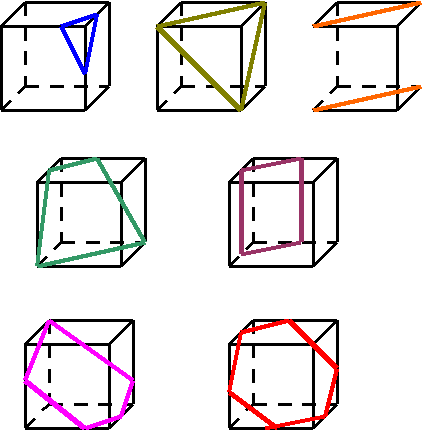
4. Тело из Трехмерии побывало во Флатландии и оставило дырку в виде треугольника. Что это могло быть?
5. Рассматриваем тела, составленные из одинаковых кубиков, «склееных» гранями. Пусть длина ребра одного куба 2см. Какую тень оставит тело на Флатландии? Начертите эту тень в натуральную величину.
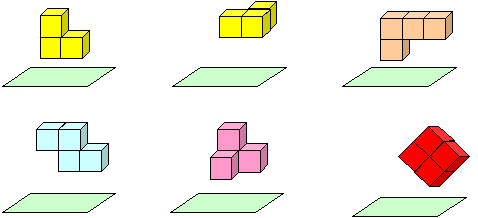
ТРИ ТЕНИ ВО ФЛАТЛАНДИИ ИЛИ ТРИ ПРОЕКЦИИ ТЕЛА НА ПЛОСКОСТЬ
1. Мы попробуем по трем теням или трем проекциям, отрарасываемых телом на плоскость, отгадать само тело. Но сначала поучимся чертить эти три тени или три проекции. Рассмотрим тело, составленное из пяти одинаковых кубиков, с ребром 1см. Как оно называется?
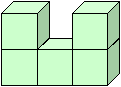
Когда геометры говорят о тех проекциях, то имеют в виду три определенных расположения тела по отношению к плоскости. Первую проекцию называют видом спереди, т.к. тело располагается по отношению к плоскости своей передней частью.
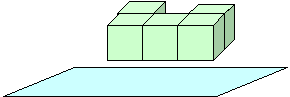
Нарисуйте в тетради первую тень или первую проекцию или вид спереди:
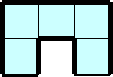
Вторую тень или вторую проекцию называют видом сверху, т.к. тело располагают верхней частью к плоскости.
Нарисуйте в тетради вторую тень или вторую проекцию или вид сверху:
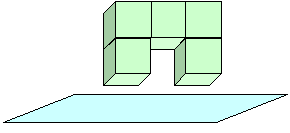
Третью тень или третью проекцию называют видом сбоку, т.в. тело поворачивают к плоскости боком.
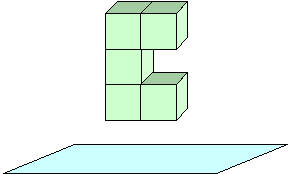
Нарисуйте в тетради эту третью тень или третью проекцию или вид сбоку.
2. Если рассмотреть плоскую фигуру, какие будут проекции у нее?
3. Какие проекции будут у отрезка?
4. Обратная задача: по трем проекциям восстановить тело.
Вид спереди вид сверху вид сбоку
1)
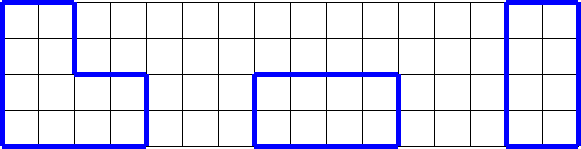
2)
3)
ТОЧКА ЛИНИЯ ПОВЕРХНОСТЬ ТЕЛО
1. Как изобразить геометрическую точку? Что может служить природным аналогом точки?
Как изобразить линию?; Какие линии вы знаете?
Повторите линию, не отрывая карандаша от бумаги и не проводя более одного раза по одному месту.
Какие линии чертят с помощью геометрических инструментов?.
2. Продолжите линию так, чтобы она имела одну ось симметрии, две оси симметрии).
3. Постройте ломаную в виде буквы русского алфавита, состоящую из двух, трех, четырех звеньев.
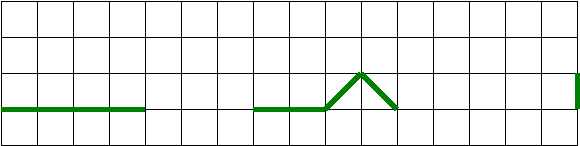
4. Постройте ломаную (рис.). Постройте еще одну ломаную, каждое звено которой параллельно одному из звеньев исходной ломанной и в два раза больше его по длине.
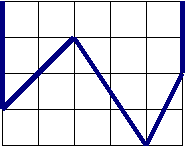
5. Постройте ломаные. Постройте ось симметрии каждой из них. Одним цветом обведите равные звенья, найдите длину ломаной.
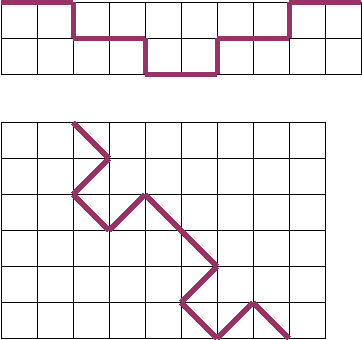
6. На рисунке изображены части ломаных и их оси симметрии пунктирной линией. Постройте ломанные полностью.
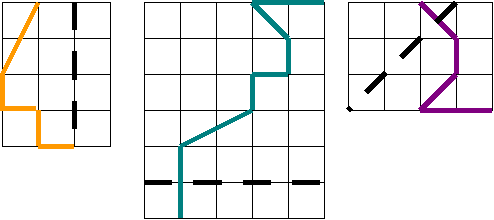
Что общего между всеми линиями, которые вы начертили?
Линии: имеют лишь одно измерение - длину; 2) линии получаются при движении точки, поэтому между словами «точка» и «линия» можно нарисовать стрелку - точка ® линия.
Есть линии, которые невозможно «уложить» на листе бумаги. Как они называются?
7. Постройте модели пространственных линий с помощью проволоки.
8. Построенные линии можно изображать на бумаге с помощью изображения куба. Перерисуйте линию, и расскажите о ней:
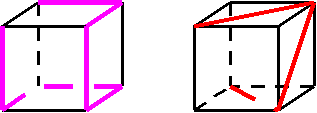
Попробуйте нарисовать три проекции этих пространственных линий на плоскости.
9. По трем проекциям постройте пространственную линию на кубе.
10. По ребрам куба идет ломаная. В ней 4 звена. Спереди она выглядит так:
Нарисуйте на кубе эту ломаную.
11. Вернемся к прямой линии. Замечательный английский математик Э. Эббот назвал пространство прямой линии Лайнландией. Кто населял Лайнландию?
В чем различие жизни отрезка в Лайнландии от жизни его во Флатландии
12. Сколько лучей определяет одна точка, выбранная на прямой, а две точки? три точки? десять точек?
Результаты занесем в таблицу.
Сколько отрезков определяет одна точка, выбранная на прямой, две точки? три точки? четыре точки? пять точек? семь точек? десять точек?
| Количество точек на прямой | Количество полученных отрезков |
| 1 | 0 |
| 2 | 1 |
| 3 | 3 |
| 4 | 6 |
| 5 | 10 |
| 10 | 10+5+6+7+9+10 |