Geum.ru

Публичный доклад муниципального автономного общеобразовательного учреждения

Вид материалаДоклад

Содержание


Результаты экзамена по математике (обязательный)
Подобный материал:
1   2   3   4   5   6   7   8   9   10



Результаты экзамена по математике (обязательный)


Итоговую выпускную работу по математике за курс основного общего образования выполняли 69 человек.

КИМы по математике за курс основной школы были направлены на проверку следующих умений:
  • выполнять действия с числами: записывать проценты в виде дроби, сравнивать действительные числа;
  • выполнять алгебраические преобразования: составлять буквенное выражение по условию задачи;
  • решать уравнения и неравенства;
  • выполнять действия с функциями: находить координаты вершины параболы, применять формулу суммы n первых членов арифметической прогрессии;
  • использовать приобретенные знания и умения в практической деятельности и повседневной жизни: решать практические расчетные задачи.

Экзаменационная работа 2011 г. состояла из двух частей. Часть 1, проверяющая освоение курса на базовом уровне, состояла из 18 заданий:

с выбором ответа из четырех предложенных вариантов (8 заданий типа А),

с кратким ответом (9 заданий типа В),

на соотнесение, условно отнесенное к заданиям типа В (В1).

В Части 1 проверялось не только владение базовыми алгоритмами, но также знание и понимание важных элементов содержания (понятий, их свойств, приемов решения уравнений, неравенств, систем уравнений и прочее), умение применить полученные знания к решению математических задач, не сводящихся к прямому применению алгоритма, а также применение знаний в простейших практических ситуациях. В основу структурирования первой части экзаменационной работы был положен содержательный принцип – задания располагаются группами в соответствии с разделами содержания, к которым они относятся. Однако последовательность этих групп в разных работах могла варьироваться.

Задания части 2 были направлены на проверку владения материалом на повышенном и высоком уровнях. Основное ее назначение – дифференцировать хорошо успевающих школьников по уровням подготовки, выявить наиболее подготовленную группу выпускников, в частности, составляющих потенциал профильных классов. Эта часть содержит 5 заданий разного уровня сложности из различных разделов курса математики, требующих развернутого ответа (с записью решения). Задания второй части расположены по нарастанию степени трудности – от стандартных и относительно простых до более сложных, предполагающих свободное владение материалом и высокий уровень математического развития. Высокий уровень выполнения заданий части 2 показан учащимися 9 А, 9 В классов (91,7% , 86,4% соответственно). 72,3% учащихся параллели 9 классов справились с выполнением заданий части 2.

При выполнении задания С1 (сокращение алгебраической дроби) были показаны следующие результаты: большая часть выпускников умеет раскладывать многочлен на множители способом группировки и с помощью формулы разности квадратов сокращать дробь. При этом отмечены случаи неправильного сокращения дробей, ошибки при разложении на множители способом группировки. Выше результаты выполнения задания показали учащиеся 9 В класса- 63,6%. В целом на параллели 9 классов только 49,3% выпускников справились с заданием.

При выполнении задание С2 (преобразование иррациональных выражений и сравнение их значений) выявлены затруднения в нахождении приближенного значения или при сравнении. Многие не знают свойств квадратного корня, забывают удвоенное произведение при возведении в квадрат двучлена, делают логические и математические ошибки в последующих рассуждениях. С выполнением задания справились 13,5% выпускников параллели 9 классов. Не справились с выполнением задания С 2 учащиеся 9 Б класса (0,0%). Невысокие показатели и у учащихся 9 А и 9 В классов (19,4% и 21,2% соответственно).

Задание С3 (нахождение числа членов арифметической прогрессии по их сумме) вызвало трудности у большинства выпускников. 12,6% учащихся параллели 9 классов справились с заданием. Эта тема является тупиковой ветвью в курсе алгебры и не имеет непосредственного продолжения в курсе 10-11 классов. Поэтому те знания, которые выпускники приобрели по этой теме в основной школе, являются, по сути дела, итоговыми. В то же время те выпускники, которые продолжат свое обучение в 10-11 классах, несомненно, будут испытывать трудности при изучении темы «Пределы», особенно вопроса «Предел последовательности». Выше показатели выполнения задания у выпускников 9 В класса – 22,7%. Низкие показатели у учащихся 9 Б класса – только 2,9% выпускников класса справились с заданием.

Задание С4 (нахождение вершины параболы, проходящей через три заданные точки) носит внутрипредметный компетентностный характер. Оно требует умений отыскать необходимую математическую модель, соответствующую условию задачи. Задание выполнили 17,8% учащихся. Из трех 9-х классов не справились с заданием учащиеся 9 Б класса (0,0%). Задание обнаружило отсутствие у выпускников умений использовать аналитический метод решения подобных заданий: составлять аналитическую модель (систему уравнений), решать ее. Выбор графического способа решения задания привел к необходимости строить график квадратичной функции, но поскольку для этого данных было недостаточно, верный ответ мало у кого получился. Это результат слабого понимания функциональной содержательной линии курса математики. Те, кто нашел верный путь решения, допустили вычислительные ошибки.

Задание С5 (текстовая задача на проценты) выполнили 17,8 % участников ГИА 9 классов школы. Основные трудности связаны с отсутствием умений увеличить на n%, уменьшить на n% и, как следствие этого, ошибки при нахождении величины после первого и второго ее изменения в процентах и при ответе на вопрос задачи.


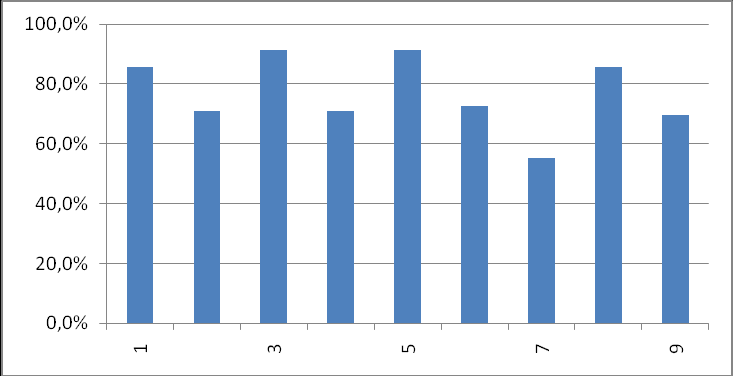
Часть А
Часть B
Часть C



№
9А
9Б
9В
Итог
№
9А
9Б
9В
Итог
№
9А
9Б
9В
Итог



1
95,8%
73,9%
86,4%
85,5%
1
87,5%
78,3%
100,0%
88,4%
1
50,0%
34,8%
63,6%
49,3%



2
87,5%
52,2%
72,7%
71,0%
2
95,8%
60,9%
86,4%
81,2%
2
19,4%
0,0%
21,2%
13,5%



3
95,8%
78,3%
100,0%
91,3%
3
79,2%
65,2%
68,2%
71,0%
3
12,5%
2,9%
22,7%
12,6%



4
75,0%
56,5%
81,8%
71,0%
4
75,0%
26,1%
86,4%
62,3%
4
27,1%
0,0%
26,1%
17,8%



5
95,8%
78,3%
100,0%
91,3%
5
79,2%
43,5%
81,8%
68,1%
5
21,9%
13,0%
18,2%
17,8%



6
83,3%
43,5%
90,9%
72,5%
6
75,0%
39,1%
72,7%
62,3%


















7
75,0%
21,7%
68,2%
55,1%
7
79,2%
52,2%
68,2%
66,7%


















8
87,5%
73,9%
95,5%
85,5%
8
79,2%
73,9%
59,1%
71,0%


















9
91,7%
52,2%
63,6%
69,6%
9
91,7%
60,9%
86,4%
79,7%













































Выполнение заданий части А