Комплекс требований к выпускнику 3 Методические материалы для государственного итогового междисциплинарного экзамена 4 > 1 Общие положения 4
| Вид материала | Документы |
- Комплекс требований к выпускнику по специальности «финансы и кредит», специализация, 1673.44kb.
- Методические указания к проведению итогового междисциплинарного Государственного экзамена, 138.42kb.
- Программа итогового государственного междисциплинарного экзамена направлению подготовки/специальности, 1092.32kb.
- Программа, вопросы и учебно-методическое обеспечение государственного итогового междисциплинарного, 1117.89kb.
- Программа итогового междисциплинарного государственного экзамена по специальности высшего, 856.01kb.
- Программа междисциплинарного итогового государственного экзамена по специальности для, 169.76kb.
- Программа междисциплинарного итогового государственного экзамена по специальности для, 196.74kb.
- Программа итогового государственного междисциплинарного экзамена 1 общие положения, 241.47kb.
- Программа итогового государственного междисциплинарного экзамена Специальность 080507., 329.85kb.
- Программа итогового государственного междисциплинарного экзамена Специальность 080507., 352.28kb.
2.Методические материалы для государственного итогового междисциплинарного экзамена
2.1Общие положения
Экзамен имеет целью оценить теоретические знания, практические навыки и умения, а также подготовленность выпускника к профессиональной деятельности.
Выпускник должен продемонстрировать знание базовых положений дисциплин, читавшихся в институте МЭК кафедрами Экономической теории, Математики и финансовых приложений, Статистики, Математического моделирования экономических процессов, Информационных технологий, Финансов, Бухгалтерского учета, Налогов и налогообложения.
Наряду с общим представлением о предметной области, экзаменуемый должен иметь представление о проблемах, возникающих в различных областях финансово-экономической деятельности и о возможных путях их преодоления.
2.2. Программа государственного итогового междисциплинарного экзамена
2.2.1.Раздел 1: Экономическая теория
- Микроэкономическая теории спроса, предложения и локального рыночного равновесия.
- Сравнительная статика (квазидинамика) локального рыночного равновесия. Нарушения локального рыночного равновесия при вмешательствах государства.
- Эластичность спроса и предложения. Практическое использование аппарата эластичности в экономическом анализе.
- Теория потребительского выбора: кардиналистская версия теории предельной полезности и ординалистская теория субституции благ.
- Теория потребительского выбора: теория выявленных предпочтений потребителя и концепция анализа качественных характеристик благ.
- Основы микроэкономической теории производства. Сравнительная статика (квазидинамика) равновесия производителя.
- Основы теории затрат производства: поведение затрат производства в краткосрочном и долгосрочном периодах.
- Теоретические концепции прибыли предприятия. Принципы максимизации прибыли: эффекты операционного и финансового левереджа.
- Основы теории организации: неоклассическая, институциональная, эволюционная, предпринимательская и агентская концепции фирмы.
- Мониторинг органического строения отраслевых рынков.
- Теория совершенной конкуренции.
- Теория рынков с наличием монопольной власти.
- Теория и модели монополистической конкуренции.
- Теория и модели олигополии.
- Микроэкономическая теория труда и заработной платы. Равновесие в условиях несовершенства рынка труда.
- Микроэкономическая теория капитала и процента: концепция межвременного выбора.
- Микроэкономическая теория капитала и процента: практические аспекты принятия инвестиционных решений.
- Рынки земли и минеральных ресурсов. Микроэкономическая теория ренты.
- Микроэкономическая теория общего равновесия: равновесие в производстве, потреблении и обмене.
- Основы экономической теории прав собственности.
- Основы микроэкономической теории неопределенности, риска и страхования.
- Теория экстерналий (внешних эффектов) и проблема «рыночного фиаско».
- Микроэкономическая теория общественного благосостояния.
- Основы теории воспроизводства общественных благ (благ коллективного доступа).
- Основы теории общественного выбора и коллективного принятия решений.
- Моделирование народнохозяйственного кругооборота и система национального счетоводства.
- Моделирование макроэкономических функций потребления и сбережений.
- Моделирование макроэкономической функции инвестиций.
- Мультипликативные эффекты, индуцированные частным сектором, государством и сектором «заграница».
- Макроэкономическое равновесие в реальном секторе: равновесная линия «инвестиции – сбережения» (IS).
- Функции денег и модели возникновения денег. Агрегирование денежной массы. Институциональное оформление кредитно-денежной сферы.
- Предложение денег: модель создания и поглощения денег банковской системой и денежные мультипликаторы.
- Спрос на деньги в кейнсианской и неоклассической монетарной теории.
- Макроэкономическое равновесие на денежном рынке: построение равновесной линии «ликвидность – деньги» (LM).
- Совместное равновесие на реальном и денежном рынках: модель Хикса – Хансена (IS – LM). Сравнительная статика в модели IS – LM и различные ситуации равновесия.
- Моделирование макроэкономической функции совокупного спроса. Влияние эффектов Кейнса, Пигу и чистого экспорта на конфигурацию линии совокупного спроса.
- Макроэкономическое равновесие на рынке труда: кейнсианская и неоклассическая интерпретации. Моделирование макроэкономической функции совокупного предложения.
- Модель общего макроэкономического равновесия: кейнсианский и неоклассический вариант.
- Макроэкономическая нестабильность в реальном секторе. Теории и модели экономического цикла.
- Макроэкономическая нестабильность на рынке труда. Теории безработицы и политика занятости.
- Макроэкономическая нестабильность в денежном секторе. Теории и модели инфляции.
- Государственный сектор экономики: налоговая система и налоговая политика.
- Бюджетная система государства и политика государственных расходов.
- Финансовая (налогово-бюджетная) стабилизационная политика государства. Управление дефицитом бюджета и государственным долгом.
- Денежно-кредитная и комбинированная стабилизационная политика государства.
- Стабилизационная политика в открытой экономике: модель «малой открытой экономики» Манделла – Флеминга.
- Основы теории международного обмена и специализации стран: базовые модели Риккардо и Хекшера – Олина.
- Посткейнсианские теории экономического роста Харрода и Домара.
- Неоклассические теории экономического роста: модель Солоу – Свана.
- Теории экономического роста с учетом фактора «человеческого капитала»: модели Лукаса и Мэнкью – Ромера – Уэйла.
Литература
Основная
- Агапова Т.А., Серегина С.Ф. Макроэкономика: Учебник / Под общ. ред. А.В. Сидоровича. — М.: ДиС, 1999.
- Борисов Е.Ф. Экономическая теория: Учебник. — М.: Юрист, 2000.
- Макроэкономика: Теория и российская практика: Учебник / Под ред. А.Г. Грязновой и Н.Н. Думной. — М: Кнорус, 2003.
- Микроэкономика. Теория и российская практика / Под. ред. А. Г. Грязновой, А. Ю. Юданова. — М.: КноРус, 2001.
- Экономическая теория / Под ред. А.Г. Грязновой, Т.В. Чечелевой. — М.: Изд-во «Экзамен», 2003.
Дополнительная
- Глобализация и мировые рынки товаров, услуг и капитала: Сборник научных статей / Под ред. Б.М. Смитиенко и В.К. Поспелова. — М.: Финансовая академия при Правительстве РФ, 2001.
- Международные валютно-кредитные и финансовые отношения: Учебник / Под ред. Л.Н. Красавиной. — М.: Финансы и статистика, 2000.
- Соколинский В.М. Государство и экономика. — М.: Финансовая академия при Правительстве РФ, 1996.
- Эффективный экономический рост. Теория и практика / Под ред. Т.В. Чечелевой. — М.: Финансовая академия при Правительстве РФ, 2000.
- Юданов А.Ю. Конкуренция: теория и практика. — Изд. 2-ое. — М.: Гном-пресс, 1998.
2.2.2.Раздел 2: Дисциплины Специальности
ЛИНЕЙНАЯ АЛГЕБРА
1. Квадратичная форма от нескольких переменных. Матрица квадратичной формы. Приведение квадратичной формы к каноническому виду. Метод Лагранжа. Закон инерции квадратичных форм. Положительно определенные квадратичные формы. Критерий Сильвестра. [1]
2. Кривые второго порядка на плоскости. Окружность и ее уравнение. Эллипс и его уравнение. Гипербола, парабола, их уравнения. Приведение общего уравнения кривой второго порядка к одному из простейших видов. [1]
3. Модель Леонтьева многоотраслевой экономики. Валовой выпуск, конечный выпуск, производственное потребление. Коэффициенты прямых затрат, их натуральная и стоимостная интерпретация. Продуктивная модель Леонтьева, критерий продуктивности. Вектор полных затрат. [1]
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
4. Производные функции одной переменной. Теорема Лагранжа, формула конечных приращений (с доказательством). Формула Тейлора в форме Лагранжа. Исследование функции с помощью производных: возрастание или убывание, экстремумы, выпуклость. Эластичность функции. [1, 2]
5. Частные производные и дифференциалы функции нескольких переменных. Производная по направлению, градиент. Свойства градиента. Формула Тейлора для функции нескольких переменных. [1, 2]
6. Экстремумы функций нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума. Наибольшее и наименьшее значения дифференцируемой функции на замкнутом ограниченном множестве. Условный экстремум. [1, 2]
7. Выпуклые функции нескольких переменных. Необходимое и достаточное условие выпуклости. Экстремумы выпуклых функций. Теорема о глобальном характере экстремума Теорема о достижении выпуклой функцией наименьшего значения в стационарной точке. [1]
8. Интегрирование функций одной переменной. Первообразная и неопределенный интеграл. Определенный интеграл. Существование первообразной для непрерывной функции. Формула Ньютона-Лейбница. Несобственные интегралы. [1, 2]
9. Степенные ряды. Теорема Абеля. Интервал и радиус сходимости степенного ряда. Интегрируемость и дифференцируемость суммы степенного ряда на интервале сходимости. Ряд Тейлора. Достаточное условие разложимости функции в ряд Тейлора. [1, 2]
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
10. Понятие дифференциального уравнения. Порядок, общее, частное и особое решение дифференциального уравнения. Интегральная кривая. Дифференциальные уравнения первого порядка. Поле направлений. Задача Коши для обыкновенного дифференциального уравнения первого порядка. [1, 2, 5]
11. Линейные дифференциальные уравнения с постоянными коэффициентами. Характеристическое уравнение. Общее решение однородного уравнения. Формирование общего решения уравнения с правой частью. [1, 2, 5]
12. Устойчивое, асимптотически устойчивое и неустойчивое по Ляпунову решения задачи Коши для системы дифференциале уравнений. Исследование устойчивости для системы линейных дифференциальных уравнений с постоянными коэффициентами по расположению собственных значений системы на комплексной плоскости. [11]
ЧИСЛЕННЫЕ МЕТОДЫ
13. Решение нелинейных уравнений. Погрешности и невязки, их взаимосвязь. Плохая обусловленность задачи. Метод половинного деления. Метод Ньютона. Сравнение методов Ньютона и половинного деления с точки зрения сходимости. [8]
14. Постановка задачи интерполяции. Интерполяция степенными полиномами. Интерполяционные полиномы Лагранжа и Ньютона. Кусочная интерполяция. Линейная интерполяция. Точность интерполяции. Факторы, определяющие точность интерполяции. Интерполяционный процесс. [8]
15. Численное решение систем обыкновенных дифференциальных уравнений. Общая характеристика методов Рунге- Кутта. Шаг, порядок метода. Типы и классификация ошибок численного решения обыкновенных дифференциальных уравнений. Выбор шага и организация автоматического выбора шага при интегрировании одношаговыми методами. [8]
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
16. Операции над случайными событиями. Аксиоматика А.Н. Колмогорова. Вероятностное пространство.. Классический способ подсчета вероятностей. Условные вероятности и независимые события. Правила сложения и умножения вероятностей. [3, 7, 10]
17. Дискретная случайная величина. Функция распределения дискретной случайной величины. Дискретные законы распределения, наиболее распространенные в практике статистических исследований. Числовые характеристики дискретной случайной величины. Математическое ожидание функции от случайной величины и неравенство Йенсена. Вогнутая функция полезности случайного дохода и отрицательное отношение к риску. [3, 7, 10]
18. Абсолютно непрерывные случайные величины. Связь функции плотности с функцией распределения. Непрерывные законы распределения, наиболее распространенные в практике статистических исследований. Начальные и центральные моменты абсолютно непрерывной случайной величины. Асимметрия и эксцесс, связь с формой графика функции плотности. Медиана и квантили непрерывных распределений. [3, 7, 10]
19. Неравенство Чебышева. Правило «трех сигм» для нормального распределения и в общем случае. Закон больших чисел, теоремы Чебышева и Бернулли. Центральная предельная теорема (ЦПТ) в форме Ляпунова. Связь ЦПТ с интегральной приближенной формулой Муавра-Лапласа. [3, 7, 10]
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
20. Генеральная и выборочная совокупности. Основные способы организации выборки. Выборочное распределение признака и его числовые характеристики. Вариационный ряд и выборочная медиана. Приближенный расчет выборочных характеристик по таблице интервальных частот. Поправка Шеппарда для выборочной дисперсии. Математическое ожидание и дисперсия выборочного среднего для бесповторной (повторной) выборки. [7, 10]
21. Статистическое оценивание параметров генерального распределения. Точечные оценки и их свойства (несмещенность, состоятельность и эффективность). Несмещенные оценки дисперсии и начальных моментов. Метод максимального правдоподобия и метод моментов. [7, 10]
22. Распределения хи-квадрат, Стьюдента и Фишера. Интервальные оценки параметров распределения, доверительная вероятность и точность оценки. Симметричные по вероятности интервальные оценки параметров нормального распределения. [7, 10]
23. Статистическая проверка гипотез: основные типы гипотез и общая логическая схема статистического критерия; характеристики качества критерия. Критерий хи-квадрат Пирсона. Проверка гипотезы о соответствии выборочного распределения теоретическому закону с данной функцией распределения. [7, 10]
ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
24. Основные классы случайных процессов: стационарные (в широком и узком смысле), нормальные, марковские. Винеровский процесс и его свойства. [12]
МНОГОМЕРНЫЕ СТАТИСТИЧЕСКИЕ МЕТОДЫ
25. Методы многомерной классификации с обучением и без обучения. Основные типы задач и алгоритмов кластерного анализа. Расстояние между объектами и мера близости. Расстояние между кластерами. Функционалы качества разбиения. Иерархические кластер-процедуры. Линейный дискриминантный анализ. при нормальном законе распределения. [13]
ДИСКРЕТНАЯ МАТЕМАТИКА
26. Функции выбора и их свойства. Основные типы функций выбора: выбор по скалярному критерию; выбор по векторному критерию, турнирный выбор. Выбор по отношению предпочтения. Нормальные функции выбора. Логическое представление функций выбора булевыми функциями. [6]
27. Графы. Основные понятия, связанные с графами. Деревья. Порядковая функция графа. Существование порядковой функции и ацикличность. Внутренняя и внешняя устойчивость. Ядро графа. Интерпретация порядковой функции, устойчивости и ядра в ситуации выбора и принятия решений. [6]
МАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ
28. Примеры задач линейного программирования (задача о банке, транспортная задача). Геометрический смысл задачи линейного программирования в случае двух и большего числа переменных. Роль угловых точек. Теоремы о существовании решения, о реализуемости решения в угловой точке. [1, 2]
29. Взаимно-двойственные задачи линейного программирования. Основная теорема двойственности (без доказательства). Теорема равновесия. Экономический смысл двойственных переменных. [1, 2]
30. Выпуклые функции нескольких переменных. Постановка задачи выпуклого программирования. Теорема Куна-Таккера. [1]
Теория оптимального управления
31. Общая постановка задачи динамического программирования. Уравнение состояний. Целевая функция отдельного шага, всего процесса. Уравнения Беллмана и порядок их решения. Задача о распределении средств между несколькими предприятиями. [13]
32. Общая постановка задачи оптимального управления для непрерывных процессов. Экономические примеры функционалов и управляющих воздействий. [9]
33. Принцип максимума Понтрягина. Преимущества использования принципа максимума Понтрягина по сравнению с другими методами оптимального управления (вариационные методы, уравнение Беллмана). [9]
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ФИНАНСОВОГО АНАЛИЗА
34. Модели финансовых потоков. Эквивалентность денежных сумм во времени. Текущая (приведенная) величина потока. Будущая (наращенная) величина потока. Внутренняя доходность потока. Понятие ренты и ее основные характеристики. Приближенные формулы для внутренней доходности ренты. [4]
35. Облигации и их характеристики. Теоремы об облигациях (зависимость стоимости купонной облигации от внутренней доходности и от времени). Дюрация облигации и ее свойства. Выпуклость облигации. Теорема об иммунизации портфеля облигаций. [4]
36. Понятия ожидаемой доходности и риска в портфельном анализе. Задача Марковица о минимизации риска. Минимальный и эффективный портфели. Рыночная линия ценной бумаги. Бета коэффициент ценной бумаги. Защитные, нейтральные и агрессивные ценные бумаги. [4]
37. Производные ценные бумаги. Пут и колл опционы. Хеджирование. Паритет цен пут и колл опционов. Оценка цены опциона в однопериодной модели. Биномиальная модель. Формула Блэка-Шоулза. [4]
Рекомендуемая литература
1. Солодовников А.С. и др. Математика в экономике. Учебник, ч. 1, 2. М.: Финансы и статистика, 2003.
2. Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании. Учебник. М.: «Дело», 2000.
3. Бабайцев В.А., Браилов А.В., Солодовников А.С. Теория вероятностей. Курс лекций. М.: Финансовая академия при Правительстве РФ, 2002.
4. Бабайцев В.А., Гисин В.Б. Математические основы финансового анализа. М.: Финансовая академия при Правительстве РФ, 2005.
5. Васенкова Е.К., Волкова Е.С., Шандра И.Г. Дифференциальные и разностные уравнения. Курс лекций. М.: Финансовая академия при Правительстве РФ, 2003.
6. Гисин В.Б. Лекции по дискретной математике, М.: Финансовая академия при Правительстве РФ, ч.1 – 2001, . ч.2 – 2003.
7. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1998.
8. Денежкина И. Е. Численные методы. М.: Финансовая академия при Правительстве РФ, 2005.
9. Киселев В.В. Теория оптимального управления. М.: Финансовая академия при Правительстве РФ, 2004.
10. Кремер Н.Ш. Теория вероятностей и математическая статистика. М.: ЮНИТИ, 2000.
11. Посашков С.А. Устойчивость решений дифференциальных уравнений. М.: Финансовая академия при Правительстве РФ, 2001.
12. Семаков С.Л. Случайные процессы: введение в теорию и приложения. М.: Финансовая академия при Правительстве РФ, 2004.
13. Солодовников А.С. Динамическое программирование. М.: Финансовая академия при Правительстве РФ, 2003.
14. Сошникова Л.А. и др. Многомерный статистический анализ в экономике. М.: ЮНИТИ, 1999.
ТЕОРИЯ ИГР
1. Задачи теории игр в экономике. Парные антагонистические игры с нулевой суммой выигрышей. Основные понятия. Решение игр в чистых стратегиях. Примеры из финансово-экономической области. [12, с. 10-50], [8, с.110-116].
2. Решение игр в смешанных стратегиях. Теорема Дж. фон Неймана о существовании решения в смешанных стратегиях. Аналитическое и геометрическое решение игры
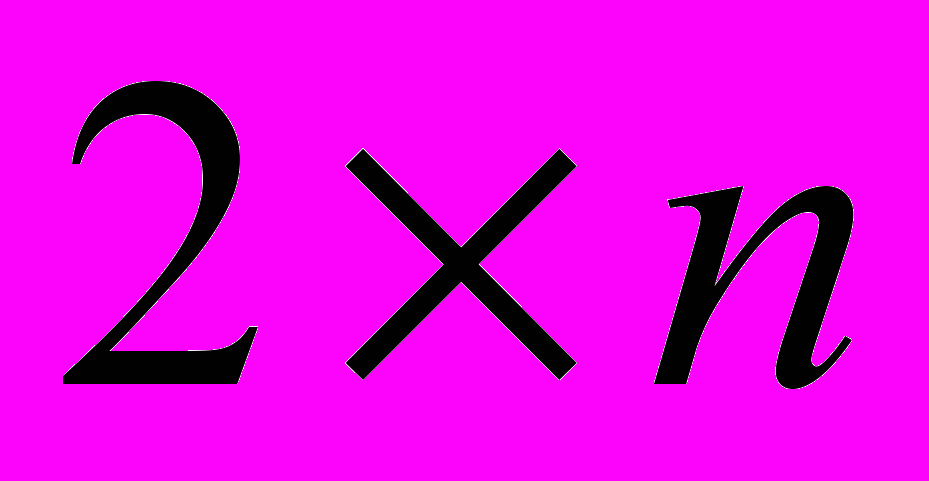и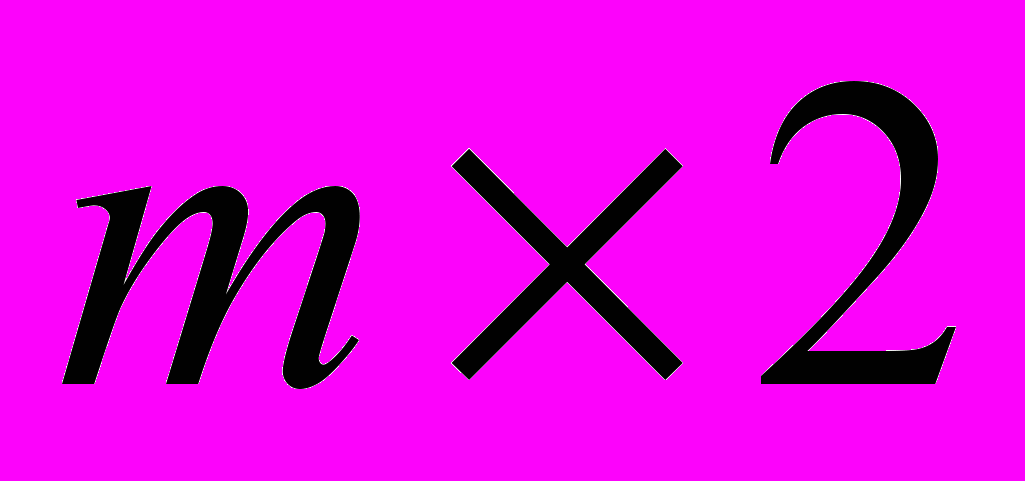 
[12, с. 51-119, 156-232],[8, с.116-129].3. Методы решения игр
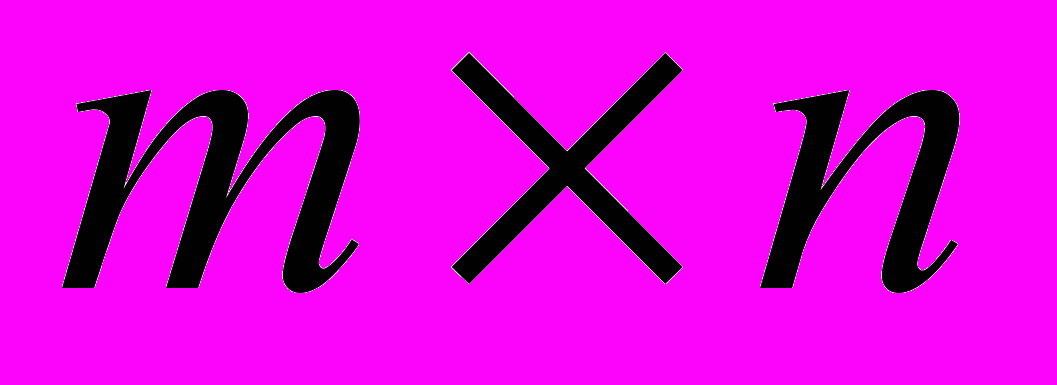. Решение игры 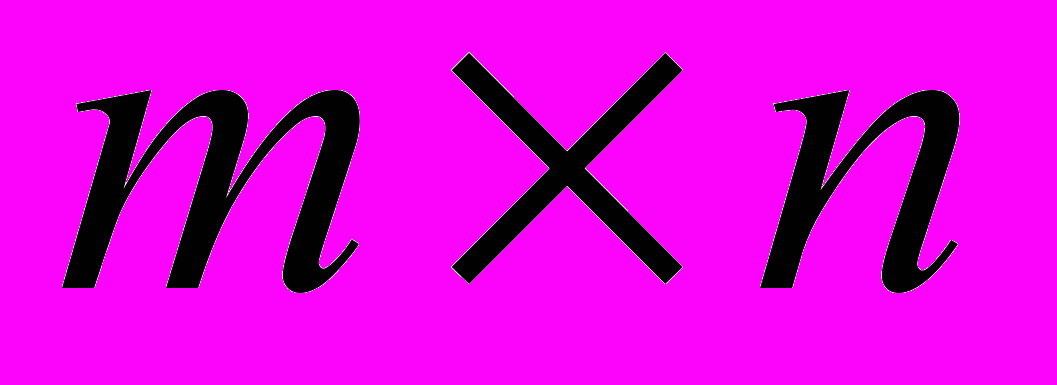методом Шепли-Сноу. Решение игры 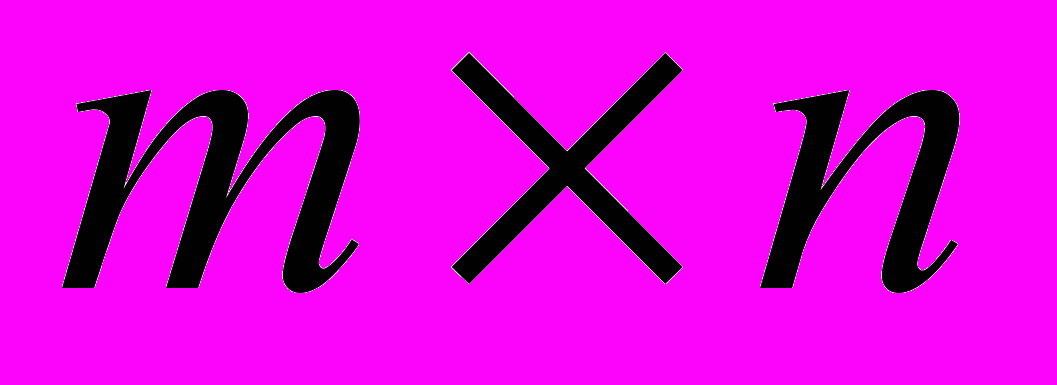приближенным методом Брауна-Робинсон. [12, с. 233-257], [8, с.129-130].4. Взаимосвязь матричных игр и линейного программирования. Примеры из финансово-экономической области. [12, с. 275-304], [8, с.129-130].
5. Принятие решения в условиях риска. Игры с природой. Критерии оптимальности стратегий Байеса, Лапласа, относительных значений вероятностей состояний природы относительно выигрышей и относительно рисков. [12, с. 305-336], [8, с.157-158].
6. Принятие решения в условиях полной неопределенности. Критерии Вальда и Сэвиджа. Максимаксный критерий. Критерий пессимизма-оптимизма Гурвица. [12, с. 337-377],[8, с.152-157].
Системный анализ
7. Методология системного подхода. Понятие системы. Свойства системы. Выделение системы из среды. [18, с.7-31].
8. Моделирование, как базовая методология анализа и синтеза систем. Модель и ее свойства. [18, с.33-60].
9. Математические модели, как средство анализа систем. [18, с.67-92].
10. Информационные процессы в системах. Информация. Сбор и передача информации. Языки для кодирования и передачи информации. [18, с.121-161].
11. Структурное моделирование экономических систем. Методология SADT структурного анализа и синтеза систем. [6].
ЭКОНОМЕТРИКА
12. Эконометрика, ее задачи и метод. Принципы спецификации эконометрических моделей. [2, с.7-29].
13. Схема построения эконометрических моделей. [2, с.30].
14. Теорема Таусса-Маркова об оптимальной статистической процедуре оценивания линейной модели множественной регрессии. [7, с. 89]
15. Исследование качества спецификации линейной модели множественной регрессии: коэффициент детерминации и F-ТЕСТ. [7, с. 113, 143].
16. Проблема и критерий идентификации эконометрической модели из линейных одновременных уравнений. [2, с. 179].
17. Оценивание параметров структурной формы эконометрической модели из линейных уравнений двухшаговым методом наименьших квадратов. [7, с. 277].
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ