Программа итогового государственного междисциплинарного экзамена направлению подготовки/специальности
| Вид материала | Программа |
- Программа междисциплинарного итогового государственного экзамена по специальности для, 169.76kb.
- Программа итогового междисциплинарного государственного экзамена по специальности высшего, 856.01kb.
- Программа междисциплинарного итогового государственного экзамена по специальности для, 196.74kb.
- Программа государственного итогового междисциплинарного экзамена по специальности 080105., 929.59kb.
- Программа итогового государственного междисциплинарного экзамена «Социология и методика, 716.79kb.
- Программа, вопросы и учебно-методическое обеспечение государственного итогового междисциплинарного, 1117.89kb.
- Программа итогового государственного междисциплинарного экзамена Специальность 080507., 352.28kb.
- Программа итогового государственного междисциплинарного экзамена Специальность 080507., 329.85kb.
- Программа государственного междисциплинарного итогового экзамена по специальности 080107, 348.09kb.
- Программа итогового государственного междисциплинарного экзамена по специальности, 265.22kb.
РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ СОЦИАЛЬНЫЙ УНИВЕРСИТЕТ
Факультет социального страхования, экономики и социологии труда
| УТВЕРЖДАЮ Декан факультета социального страхования, экономики и социологии труда ____________________/Грунин А.А./ | УТВЕРЖДАЮ и.о.Заведующий выпускающей кафедрой социальной статистики и демографии ____________________/Лукьянец А.С./ |
| Принято Решение Совета факультета от «____» _______ 20__г. протокол № ____ | Утверждено на заседании кафедры от «18» ОКТЯБРЯ 2011 г. протокол № 3 |
ПРОГРАММА
ИТОГОВОГО ГОСУДАРСТВЕННОГО МЕЖДИСЦИПЛИНАРНОГО ЭКЗАМЕНА
НАПРАВЛЕНИЮ ПОДГОТОВКИ/СПЕЦИАЛЬНОСТИ
080601.65 «СТАТИСТИКА»
Москва, 2011г.
ВВЕДЕНИЕ
Программа государственного экзамена разработана ВПО по специальности 080601.65 – «Статистика» и является базой для формирования оценочных заданий, предназначенных выпускнику на экзамене.
Проведение государственного экзамена позволяет выявить уровень теоретической подготовки выпускников, их готовность решать профессиональные задачи в области социально-экономической статистки, демографии, управления персоналом, проведения социологических исследований в социальной сфере.
При оценке знаний выпускников следует руководствоваться требованиями к профессиональной подготовке экономиста с высшим образованием по данной специальности.
Специалист должен знать:
- Теоретические основы и закономерности функционирования экономики, включая переходные процессы;
- Принципы принятия и реализации социально-экономических и управленческих решений;
- Закономерности формирования рынков товаров, услуг и труда;
- Экономическое моделирование экономических и социальных процессов на различных уровнях управления;
- Приемы и методы анализа статистической информации для количественной и качественной оценки социально-экономической ситуации на микро, мезо, макро и глобальном уровнях;
- Методы и приемы анализа занятости, социальной сферы, демографических процессов.
Специалист должен уметь:
- Организовывать статистическое наблюдение для сбора количественной информации о социальных и других объектах различными методами;
- Осуществлять процесс сбора и обобщения статистической информации об исследуемом объекте, систематизировать и формализовать полученные массивы данных;
- Проводить классификацию и типологию различных признаков объекта для получения качественно однородных групп.
- Проводить исследования социально-экономических процессов и явлений с использованием расчетов статистических показателей, характеризующих любые объекты наблюдения;
- Готовить к публикации результаты и итоги проведенных статистических исследований;
- Разрабатывать и обосновывать варианты эффективных управленческих решений, основанных на анализе и прогнозе процессов и явлений;
- Использовать основные и специальные методы статистического анализа и прогноза и получения информации в профессиональной деятельности;
- Выявлять проблемы социально-экономического характера при анализе конкретных ситуаций, предлагать способы их решения и оценивать ожидаемые результаты;
- Формировать политику организации в области проведения статистического учета, анализа и прогноза.
Специалист должен владеть:
- Методами организации и проведения статистического наблюдения, сбора и обобщения информации;
- Методами анализа и прогноза массивов статистической информации;
- Методами разработки и проведения социологических обследований для получения информации в социальной сфере;
- Навыками применения методов статистического анализа в профессиональной деятельности.
Учитывая весь набор требований к подготовке специалистов данного профиля, предлагаемая программа состоит из совокупности предметов блока общепрофессиональных дисциплин: статистика (общая теория статистики, социально-экономическая статистика), демография и статистика населения - специальности 080601.65 «Статистика» и носит комплексный характер.
I БЛОК “ОБЩАЯ ТЕОРИЯ СТАТИСТИКИ»
1. Предмет статистической науки. Теоретические основы, категории статистики.
Основные черты и особенности предмета статистики:
- исследование массовых и социально-экономических явлений и процессов;
- изучение количественной стороны качественно определённых общественных явлений и процессов в конкретных условиях места и времени;
- характеристика структуры общественных явлений, то есть изучение внутреннего строения массовых явлений;
- исследование уровня и структуры явления в динамике.
Общие правила статистического исследования опираются на положения социально- экономической теории и законы динамики, согласно которым изучаемые явления и процессы рассматриваются в развитии, взаимной связи и причинной обусловленности.
Положения социально-экономической теории и принципы диалектического метода познания составляют теоретическую базу статистики.
Важнейшими категориями статистической науки являются:
- категория признака;
- категория совокупности;
- показатель-категория.
2. Метод статистики, стадии статистического исследования. Закон больших чисел.
Совокупность разнообразность методов образует системное понятие «статистическая методология».
Статистическое исследование и его стадии:
- статистическое наблюдение;
- первичная обработка, сводка и группировка результатов наблюдения;
- анализ получаемых материалов.
Статистические методы рассматриваются как методы анализа количественных данных.
Метод массового наблюдения. Метод статистических группировок и таблиц. Метод анализа с помощью обобщающих показателей. Статистическая закономерность. Закон больших чисел, как выражение диалектики случайного и необходимого.
3. Система показателей статистики, понятие, виды, их квалификация.
Система статистических показателей – это совокупность взаимосвязанных показателей, имеющая одноуровневую или многоуровневую структуру и нацеленная на решение конкретной статистической задачи.
Различают конкретный статистической показатель и показатель – категорию. Конкретный статистический показатель характеризует размер, величину изучаемого явления или процесса в данном месте и в данное время.
Показатель – категория отражает сущность, общие отличительные свойства конкретных статистических показателей одного и того же вида без указания места, времени и числового значения.
Все показатели по охвату единиц совокупности разделяются на индивидуальные и связные, а по форме выражения – на абсолютные, относительные и средние.
Важным классификационным признаком является также временной фактор (показатели – моментные, интервальные); по охватывающей территории (общетерриториальные, региональные, местные); по числу объектов (однообъектные, многообъектные); по способу получения (объёмные, расчётные).
4. Проблемы организации и проведения специально организованного статистического наблюдения. Понятие и программа.
Проблемы организации и проведения специально-организованного статистического наблюдения. Понятие и программа.
Специально-организованное наблюдение – это одна из форм статистического наблюдения (наряду со статистической отчетностью и регистром).
Специально организованное наблюдение (СОН) проводится с целью получения сведений, отсутствующих в отчетности, или для проверки данных. Наиболее простым примером такого наблюдения является перепись.
Перепись – это специально организованное наблюдение, повторяющееся, как правило, через равные промежутки времени с целью получения данных о численности, составе и состоянии объекта статистического наблюдения по ряду признаков.
Характерными особенностями переписи являются:
- одновременность поведения ее на всей территории, которая должна быть охвачена обследованием;
- единство программы наблюдения;
- регистрация всех единиц наблюдения по состоянию на один и тот же критический момент времени.
Программа наблюдения, приемы и способы получения данных по возможности должны оставаться неизменными. Это позволяет обеспечить сопоставимость собираемой информации и получаемых в ходе разработки материалов обобщающих показателей.
Российская практическая статистика проводит переписи населения, материальных ресурсов, многолетних насаждений, неустановленного оборудования, незавершенного строительства и др. Из всех переписей наиболее известна перепись населения Первая всеобщая перепись населения России была проведена в 1897 г., а последняя в 2002 г. В ходе пробной переписи населения (11-18 октября 2000 г., охватывающей около 100 тыс. человек) был опробован проект программы Всероссийской переписи населения 2002 г. Программа имела преемственность с прошлыми переписями населения. И содержала вопросы, касающиеся структуры населения (пол, возраст, семейное положение, национальность) и содержала вопросы, отражающие изменения в социально-экономической сфере, которые произошли в стране с начала 90-х годов двадцатого века.
Кроме переписей статистика проводит и другие специальные организованные наблюдения, например, в начале 2001 г. было проведено сплошное статистическое обследование малых предприятий по итогам работы за 2000 год, целью которого было получение полного перечня малых предприятий и сведений о производимых ими товаров и услуг.
СОН – модульное обследование – периодические переписи остатков стратегического сырья, материалов и др.
Под программой статистического наблюдения понимается перечень тех признаков, которыми каждая единица наблюдения должны быть охарактеризована, т.е. это перечень вопросов, на которые в процессе наблюдения должен быть получен ответ. Новые специальные наблюдения – мониторинг (оперативная информация), пилотные обследования (индивидуальных предпринимателей).
5. Программно - методологические вопросы организации первичного учёта и отчётность в отдельных областях экономики.
В российской статистике традиционно сложились две основные организационные формы статистического наблюдения:
- Отчетность (предприятий, организаций, фирм, компаний и т.д.)
- Специальное статистическое наблюдение.
Отчетностью называется такая организационная форма статистического наблюдения, при которой в установленные сроки и в установленном порядке в соответствующие статистические органы поступают сведения о деятельности подотчетных предприятий, организаций т.д. в виде официального документа – статистического отчета.
Статистическая отчетность обязательна для всех подотчетных организационно - правовых структур на всех уровнях управленческой иерархии и имеет строгую периодическую силу, т.к. все без исключения формы статистической отчетности подписываются руководителем предприятия, организации, фирмы и т.д.
Отчетность является важнейшей формой статистического наблюдения, в ней содержатся основные первичные учетно-статистические данные о состоянии и деятельности предприятий, организаций и т.д. Отчетность составляется на основе данных первичного учета и является их обобщение.
Первичным учетом в статистике называется первоначальная, систематическая, производимая по факту совершения, регистрация в формах первичных учетных документов, фактов, событий, актов производственно-хозяйственной деятельности предприятий, организаций, фирм и т.д.
Примером документов первичного учета являются накладные на отпуска товарно-материальных ценностей со склада и т.д.
Все формы статистической отчетности утверждают органы государственной статистики. Утвержденные и действующие формы статистической отчетности содержат системы показателей, составляющих программу отчетности. Перечень показателей нацелен на более полное представление и отражение развития отраслей народного хозяйства и экономики страны в целом.
Статистическая отчетность подразделяется на государственную и внутриведомственную отчетность.
По своему содержанию формы статистической отчетности могут быть типовыми и специализированными.
Типовой является отчетность, содержащая единую программу для всех предприятий и организаций, а также всех отраслей народного хозяйства.
Специализированной является отчетность, предназначенная для предприятий, организаций и учреждений, имеющих определенные особенности, содержащая наряду с общими показателями, имеющимися в типовой отчетности; показатели специфические для определенных организационно-правовых форм, видов деятельности и производства.
Каждая форма отчетности (типовая) имеет определенный номер, название с указанием периодичности или даты представления, реквизиты предприятия (организации), его административно-территориальные нахождения, коды по классификаторам и сведения по специальной программе. Госкомстатом Российской Федерации утверждены следующие унифицированные формы статистического наблюдения:
- Форма №1 – предприятие «Основные сведения о деятельности предприятий» - годовая;
- Форма №П–1 «Сведения о производстве и отгрузке товаров и услуг» – месячная
- Форма № П – 2 «Сведения об инвестициях» – квартальная;
- Форма №П–3 «Сведения о финансовом состоянии организаций» – месячная;
- Форма №П – 4 «сведения о численности заработной платы и движений работников» – месячная;
- Форма №П – 5 «Основные сведения о деятельности малого предприятия» - квартальная.
Использование унифицированных форм статистического наблюдения позволяет получить комплексную информацию по всем видам деятельности предприятий и о его финансовом положении, к какой бы отрасли оно не относилось.
Важным условием организации наблюдения на основе унифицированных форм является разработка и утверждение форм первичной документации, адаптированной к требованиям международных стандартов бухгалтерского учета, а также их электронной версии. Госкомстатом Российской Федерации разработан альбом унифицированных форм первичного учета, включающий формально учету труда и его оплаты, основных средств и нематериальных активов, материалов, малоценных и быстроизнашивающихся предметов, работ в капитальном строительстве и др.
Внедрение унифицированных форм первичной учетной документации способствует повышению качества, достоверности и сопоставимости результатов наблюдения.
В дополнении к унифицированным формам используются формы наблюдения, отражающие специфическую информацию отраслевого характера. Это так называемая специализированная отчетность.
Имеются специализированные формы наблюдения на транспорте, в связи, торговле, строительстве, для предприятий естественных монополий и др.
В целях усиления контроля за увеличением сбора налогов и сокращения расходов федерального бюджета с 1 января 1997 года введена месячная форма государственного статистического наблюдения о составе кредиторской задолженности организаций бюджетного – получателей. Для наблюдения за деятельностью финансово-промышленных групп (ФПГ) введена форма наблюдения №1 – ФПГ, данные которой позволяют охарактеризовать ФПГ, оценить структуру по видам деятельности, ресурсный потенциал, масштабы производства продукции и инвестиционной деятельности.
6. Организационные и программно - методологические вопросы статистического наблюдения. Цель, объект, виды наблюдения.
Статистическое наблюдение производится строго в соответствии с планом статистических исследований. При подготовке и проведении статистического наблюдения необходимо решить целый ряд вопросов, который можно подразделить на:
1. Программно – методологические.
2. Организационные.
Программно – методологическими вопросами определяется цель статистического наблюдения, устанавливается объект и единица наблюдения, разрабатывается инструментарий, обязательный для каждого участника наблюдения, определяется круг признаков, характеризующих единицу наблюдения, по которым производится регистрация данных, или разрабатывается программа.
Программой статистического наблюдения называется перечень вопросов или признаков, на которую должны быть получены ответы по единицам наблюдения.
Организационные вопросы охватывают сроки и место проведения наблюдения, положение об организационной стороне наблюдения, подготовку и расстановку кадров и другие, обычно включаемые в организационный план статистического наблюдения. В организационном плане прежде всего указываются органы, выполняющие статистическое наблюдение. Это могут быть органы государственной статистики РФ или конкретные службы. Четко определяются и разграничиваются права и обязанности конкретных учреждений и организаций, участвующих в наблюдении.
Цель определяет объект статистического наблюдения.
Объект статистического наблюдения представляет совокупность явлений, предметов и т.д., охватываемых наблюдением. Объектом может быть население при переписи, предприятия, города, населенные пункты, персонал фирмы или его отдельные категории, словом, это исследуемая статистическая совокупность. Единица наблюдения представляет первичный элемент объекта статистического наблюдения.
Для реализации программы статистического наблюдения разрабатывается статистический инструментарий. Традиционно он включает инструкции по проведению наблюдения и регистрации данных, бланки документов, в которые заносится информация и др. носители первичной информации. Это анкет, табеля, формы отчетности, переписные листы.
В настоящее время получают распространение технические носители информации, т.е. совершенствуется так называемая безбумажная технология сбора информации и введения ее в ЭВМ.
Статистическое наблюдение подразделяется (вид):
1. По охвату единиц совокупности на сплошные и несплошные.
2. По времени проведения на непрерывные (текущие), единовременное и периодическое.
7. Основные принципы и правила использования абсолютных и относительных величин в статистическом анализе.
Важно отметить, что в процессе экономико-статистического анализа абсолютные и относительные величины должны рассматриваться во взаимосвязи, т.е. пользоваться относительными величинами нужно не формально, а представлять, какая абсолютная величина скрывается за каждым относительным показателем. Особенно важно соблюдать это положение при расчете относительных величин динамики.
Одно из главных требований, которое предъявляется при исчислении относительных величин, заключается в необходимости обеспечения сопоставимости сравниваемой величины и величины, принятой за базу сравнения. Прежде всего должна быть обеспечена сопоставимость по методологии расчета сравниваемых показателей, по степени охвата объектов исследуемой совокупности и другим существующим обстоятельствам.
Анализ изменений явлений во времени.
Важной проблемой построения динамических рядов является проблема сопоставимости уровней этих рядов, относящихся к различным периодам. Соблюдение требования сопоставимости уровней ряда означает, что полезно лишь такое сравнение, которое учитывает существо изучаемого явления цель, к которой оно приводит. Показатели динамического ряда, подлежащие сопоставлению, должны быть однородны по экономическому содержанию.
Для этого прежде всего должна быть обеспечена одинаковая полнота охвата различных частей явления. Требование одинаковой полноты охвата различных частей изучаемого объекта означает, что уровни динамического ряда за отдельные периоды времени должны характеризовать размер того или иного явления по одному и тому же кругу, входящих в его состав частей. Например, при характеристики динамики численности студентов высших учебных заведений по годам нельзя в дин год учитывать только численность студентов дневного обучения, а в другие – численность студентов всех видов обучения.
При сопоставлении уровней динамического ряда может возникнуть вопрос учета одинаковых границ территории.
При определении сравниваемых уровней динамического ряда необходимо использовать единую методологию их расчета. Особенно часто эта проблема возникает при международных сопоставлениях.
Приведение к сопоставимому виду разнообразной продукции.
При анализе показателей объема продукции, переменной в ценностных единицах, следует учитывать:
1. Со снижением времени происходит изменение цен;
2. Существует несколько видов цен (цены производителей и цены потребителей).
В этой связи при характеристике стоимостных показателей объема продукции во времени должно быть устранено влияние цен. На практике для решения этой задачи количество этой продукции, произведенное в разные периоды, оценивается в ценах одного периода, которые называются фиксированными или сопоставимыми.
Одним из условий сопоставимости уровней интервального динамического ряда является равенство периодов, за которые приводятся данные.
Все выше названные обстоятельства следует учитывать при подготовке информации для анализа изменений явлений во времени.
8. Абсолютные величины, виды, способы исчисления.
Абсолютные статистические величины: индивидуальные и суммарные. Как обобщающие показатели абсолютные величины являются всегда суммарными величинами, которые могут быть показателями численности совокупности (число предприятий, число рабочих, число студентов) и показателями объема признаков (заработная плата рабочих, объем выпуска товаров и услуг и т.п.)
Абсолютные величины – именованные числа, имеющие определенную размерность и единицы измерения. Они характеризуют показатели на определенный момент времени или за период.
На момент времени абсолютные величины показывают состояние явления (численность населения, студентов, вузов, предприятий); за период – результаты процесса (объем производства товаров и услуг, товарооборота и т.д.).
В первом случае абсолютные показатели являются моментными показателями, во втором – интервальными. Такое деление абсолютных величин имеет большое значение при расчете средних уровней в рядах динамики.
В зависимости от причин и целей в статистике применяются натуральные, условно-натуральные, денежные и трудовые единицы измерения.
Натуральные единицы измерения могут быть простыми (тонны – перевезенный груз) и составными (тонна – километр – грузооборот).
В международной практике используются следующие натуральные единицы измерения: метры, километры, мили, литры, баррели, штуки, килограммы и т.д.). Условно-натуральные измерители применяются в тех случаях, когда какой-либо продукт имеет несколько разновидностей. Тогда общий объем можно определить исходя из потребительского свойства всех разновидностей продукта. Так, мыло разных сортов переводится в условное мыло с 40%-ным содержанием жирных кислот; консерванты различного объема переводятся в условные консервные банки объемом 353, 4 см3; различные виды органического топлива – в условное топливо с теплотой сгорания 29,3 мДж/кг (7000 ккал/кг).
Перевоз в условно-натуральные единицы измерения осуществляется на основе специальных коэффициентов, рассчитываемых как отношение потребительских свойств отдельных разновидностей продукта к его эталонному значению.
9. Относительные величины, их виды, сущность, условия применения, способы расчёта, взаимосвязи между ними.
Относительные величины (показатели) характеризуют количественное соотношение сравниваемых абсолютных величин. Их получают в результате сравнения двух показателей: числитель отношения – сравниваемая величина; знаменатель – база сравнения (основание сравнения).
Если сравнивают одноименные величины, то их выражают в коэффициентах, процентах, промилле. При сопоставлении разноименных величин наименование относительных величин образуются от наименований сравниваемых величин: плотность населения – чел./км2; урожайность – ц/га и т.д.).
В зависимости от задач, содержания и познавательного значения, выражаемых количественно соотношений, различают следующие виды относительных показателей:
1. планового задания (договорных обязательств) – упл / уо
2. выполнения плана (договорных обязательств) – у2/упл
3. динамики – у1/уо
4. структуры;
5. интенсивности и уровня экономического развития;
6. координации;
7. сравнения.
Относительная величина динамики может быть получена путем умножения относительных величин планового задания и выполнение плана:
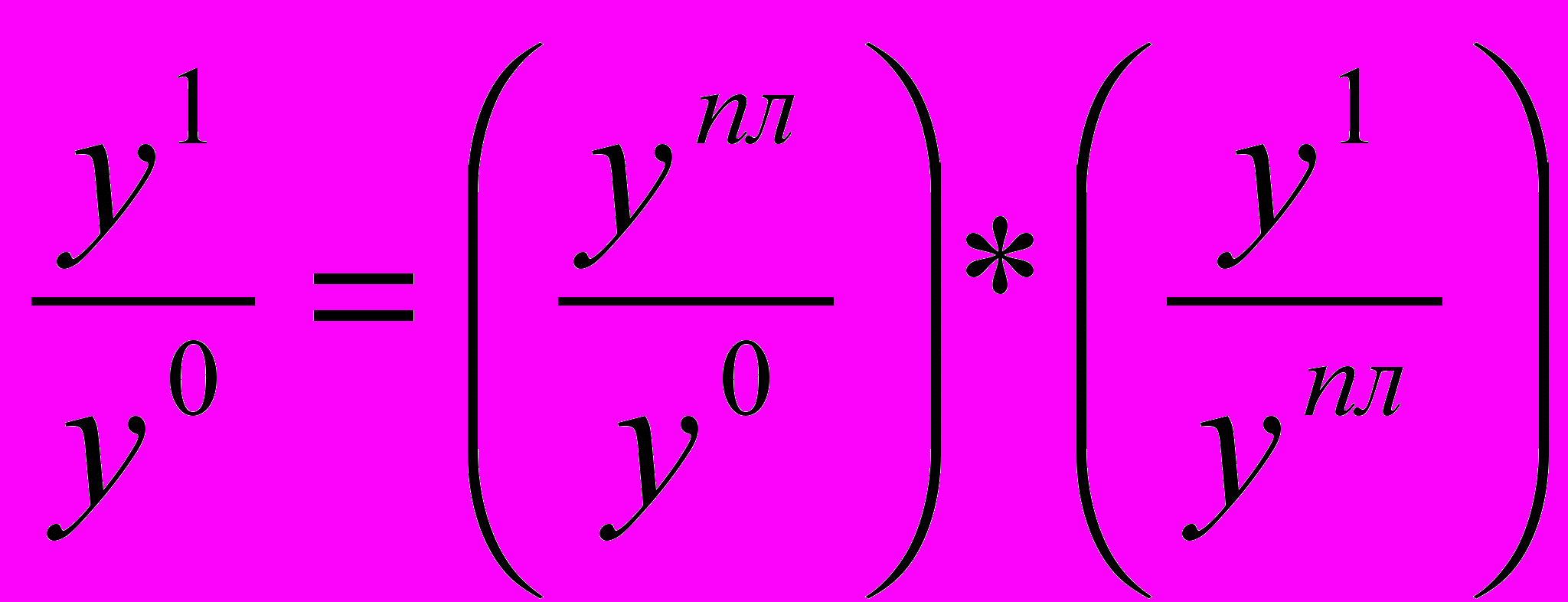
Одно из главных требований, предъявляемых при исчислении относительных величин, заключается в необходимости обеспечения сопоставимости сравниваемой величины и величины, принимаемой за базу. Прежде всего должна быть обеспечена сопоставимость по методологии расчета сравниваемых показателей, по степени охвата объектов исследуемой совокупности.
10. Основные направления совершенствования способов и группировки статистических данных.
На практике при обработке массовых данных задача расчленение единиц изучаемой совокупности на группы по отдельным признакам решается порой более сложными приемами, разработанными в последние годы и требующими использования компьютеров. Особенно это относится к группировкам по нескольким признакам, т.е. на основе множества признаков. Для этой цели разработаны так называемые методы многомерной классификации: классификация на основе многомерной средней, кластерный анализ, метод главных компонентов.
11. Задачи и виды группировок: структурные, типологические, аналитические.
Группировкой называется расчленение единиц статистической совокупности на группы, однородные по какому-либо одному или нескольким признакам.
Группировка позволяет систематизировать данные статистического наблюдения, которые в результате группировки превращаются в упорядоченную информацию, пригодную для дальнейшего статистического анализа.
Основная цель группировки:
- выявить важнейшие социально-экономические типы явления;
- дать характеристику состава (структуры) совокупности по какому-либо признаку в пределах уже определенного социально-экономического типа;
- выявить взаимосвязи в изменениях изучаемых признаков.
В зависимости от цели выделяют следующие виды статистических группировок: типологическую, структурную и аналитическую.
12. Ряды распределения и их познавательные возможности. Понятие и виды (атрибутивные, вариационные, дискретные и интервальные).
Рядом распределения называется упорядоченное распределение совокупности по определенному варьирующему признаку (атрибутивному или вариационному) на однородные группы.
В зависимости от признака, положенного в основе построения ряда распределения, различают атрибутивные и вариационные распределения.
Атрибутивным называется ряд распределения, построенный по качественным признакам, т.е. признакам, не имеющим числового выражения и характеризующим свойство, качество изучаемого социально-экономического явления.
Атрибутивные ряды распределения характеризуют состав совокупности по существенным признакам. Взятые за несколько периодов, эти данные позволяют исследовать изменение структуры. Число групп атрибутивного ряда распределения адекватно числу градаций, разновидностей атрибутивного признака.
Вариационным называется ряд распределения, построенный по количественному признаку, т.е. признаку, имеющему числовое выражение.
Основными элементами вариационного ряда распределения являются:
- варианты числовых значений количественного признака;
- частоты – численности отдельных вариантов или каждой группы вариационного ряда, т.е. числа, которые показывают, как часто встречаются те или иные варианты (значения признака) в ряду распределения.
Сумма всех частот определяет численность всей совокупности.
В зависимости от характера вариации изучаемого признака различают дискретные и интервальные вариационные ряды распределения.
Дискретным вариационным рядом распределения называется ряд, в котором группы составлены по признаку, изменяющемуся дискретно. Например, распределение рабочих предприятия по тарифному разряду.
Интервальным вариационным рядом распределения называется ряд, в котором группированный признак, составляющий основание группировки, может принимать в определенном интервале любые значения. Интервальный ряд распределения целесообразно строить, прежде всего, при непрерывной вариацией признака, а также если дискретная вариация проявляется в широких пределах, т.е. число вариантов дискретного признака достаточно велико.
Правило и принципы построения интервальных рядов распределения аналогичны правилам и принципам построения статистических группировок. Примером интервального вариационного ряда может служить распределение сотрудников лизинговой компании по уровню дохода.
Основная задача рядов распределения заключается в выявлении характера и закономерности распределения.
Анализ рядов распределения можно наглядно проводить на основе их графического изображения. Для этой цели стоят полигон, гистограмму, огиву и кумуляту распределения.
Полигон – используется для изображения дискретных вариационных рядов.
Гистограмма применяется для изображения интервального вариационного ряда.
При помощи кумуляты изображается ряд накопленных частот.
Графическое изображение рядов распределения позволяет наглядно представить распределение данных статистического наблюдения.
13. Нормальное распределение и его свойства.
В практике статистического исследования приходится встречаться с самыми различными распределениями. Если непрерывная случайная величина имеет плотность распределения:
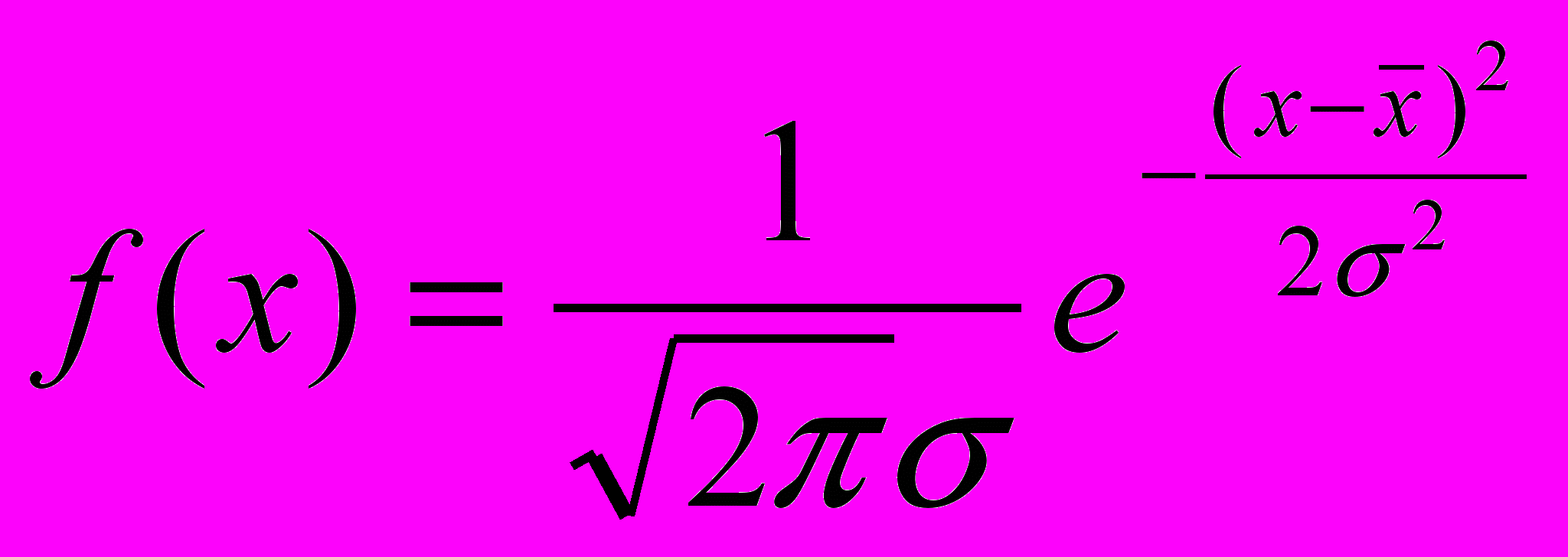,то оно подчиняется закону нормального распределения. Для построения кривой нормального распределения надо знать два параметра:
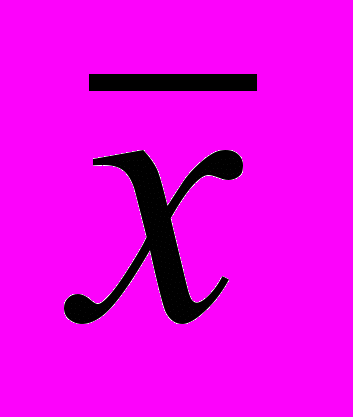и 
. Если средняя арифметическая (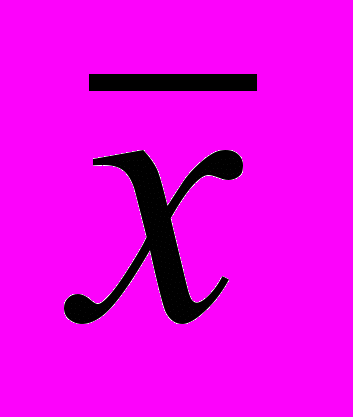) не меняется, то растет величина среднего квадратического отклонения, распределение имеет более плосковершинный характер. При одной и той же величине среднего квадратического отклонения, но с разными значениями средней арифметической, кривая нормального распределения, не меняя своей формы, сдвигается вдоль оси абсцисс (вправо или влево).Особенности кривой нормального распределения:
1. Кривая симметрична относительно максимальной ординаты. Максимальная ордината соответствует значению
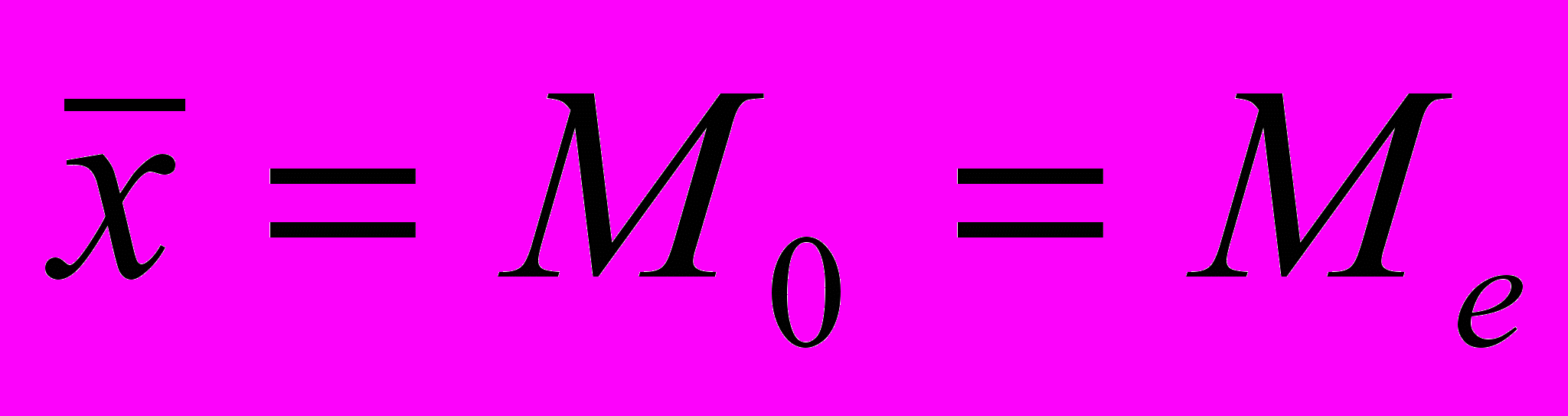, ее величина равна 
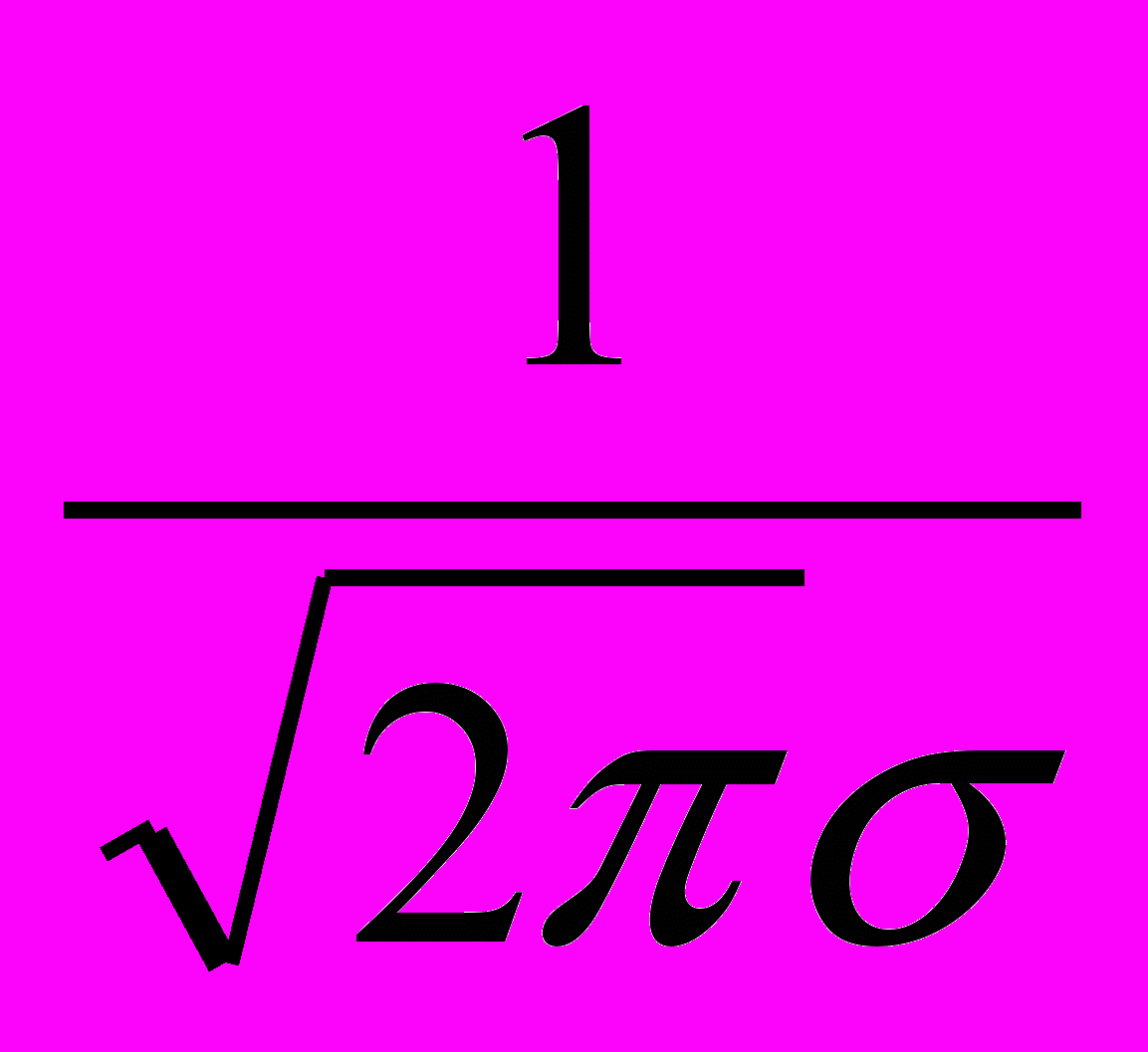.2. Кривая асимптотически приближается к оси абсцисс, продолжаясь в обе стороны до бесконечности. Следовательно, чем больше значение отклоняется от
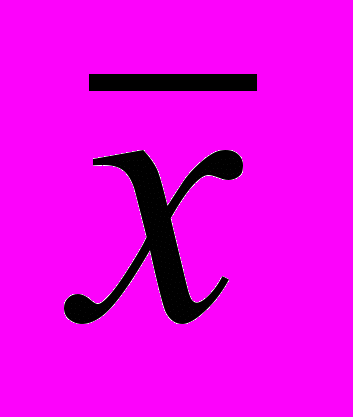, тем реже они встречаются. Одинаковые по абсолютному значению, но противоположные по знаку отклонения значений переменной х от 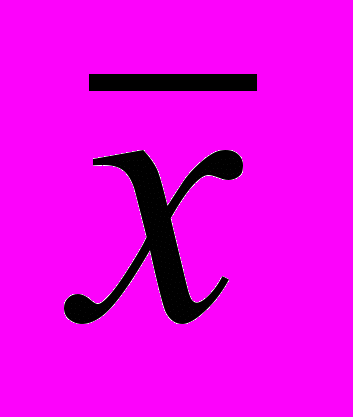равновероятны.3. Кривая имеет две точки перегиба, находящиеся на расстоянии
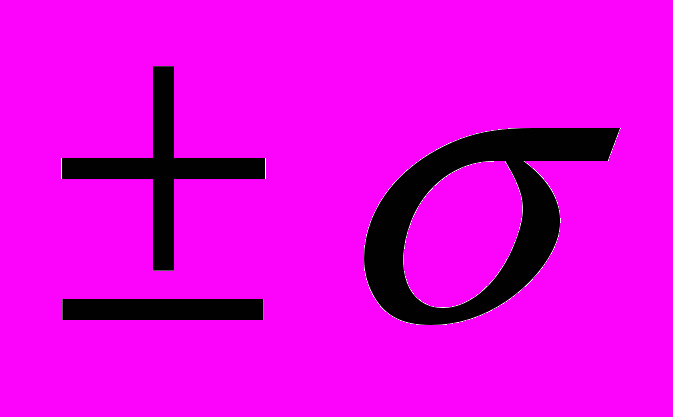от 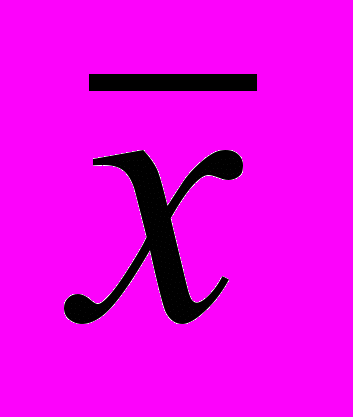.4. При
с увеличением кривая становится более пологой. При 
с изменением 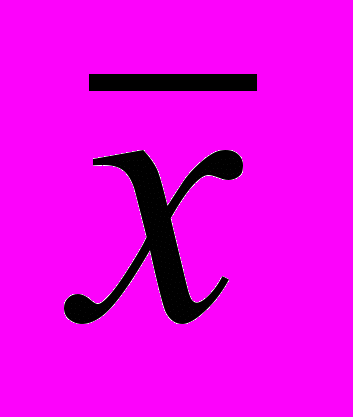кривая не меняет свою форму, а лишь сдвигается вправо или влево по оси абсцисс.5. В промежутке
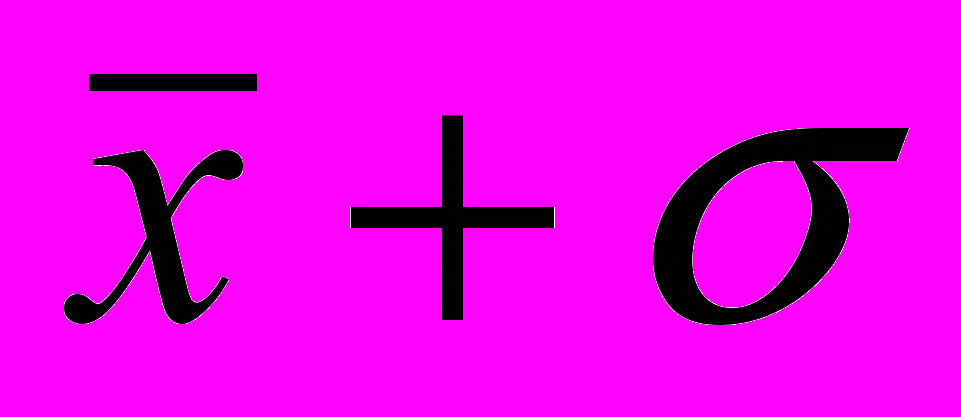находится 68,3% всех значений признака. В промежутке 
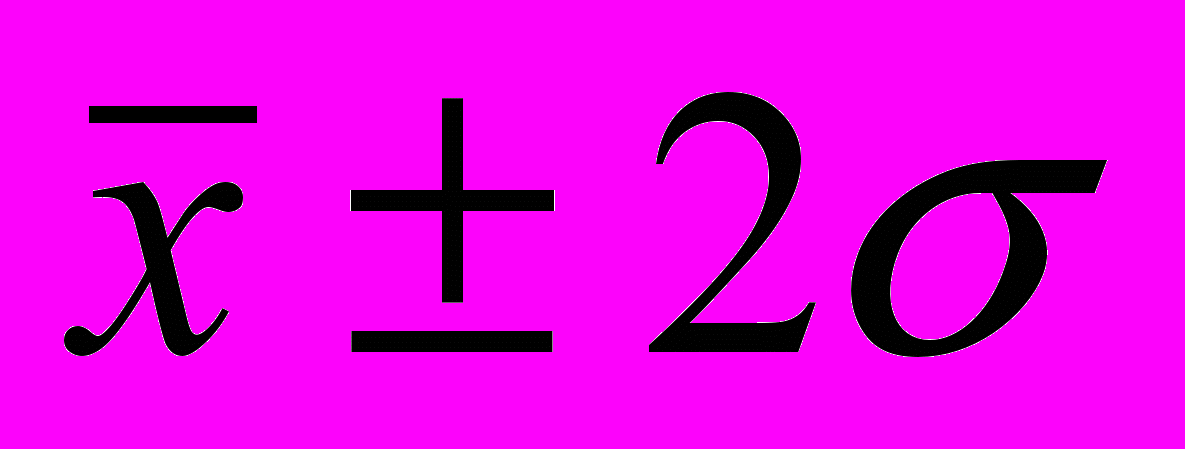находится 95,4% всех значений признака. В промежутке 
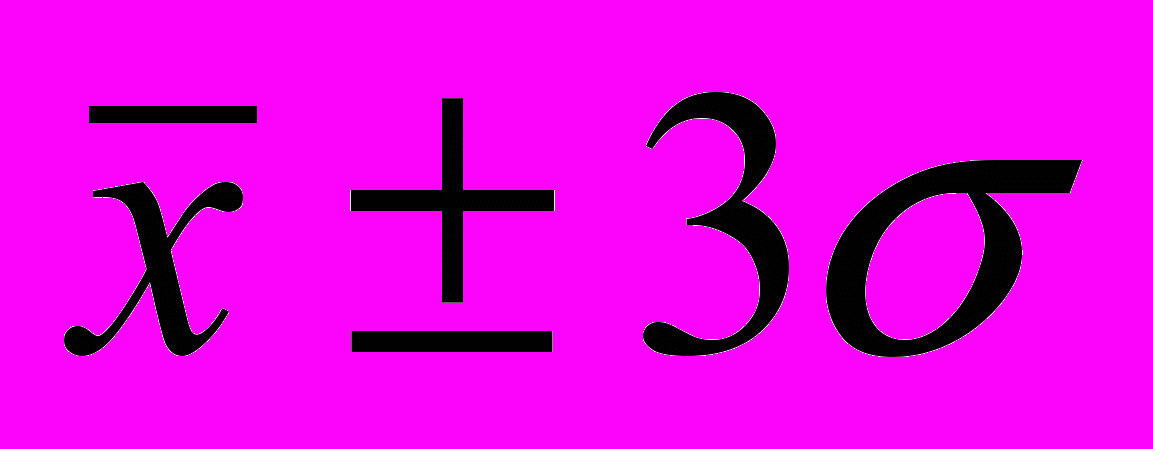находится 99,7% всех значений признака (правило «трех сигм»).Нормальное распределение возможно в том случае, когда на величину признака влияет большое число случайных причин. Действие этих причин независимо, и ни одна из причин не имеет преобладающего влияния над другими.
14. Расчёт средних величин и их роль в управлении экономикой.
Среди обобщающих показателей, характеризующих статистические совокупности, большое значение имеют средние величины.
Средняя величина – это обобщающая характеристика множества индивидуальных значений некоторого количественного признака. Средняя, являясь функцией множества индивидуальных значений, представляет своим значением всю совокупность и отражает то общее, что присуще ее единицам.
Практическое применение средних величин как обобщающих характеристик явлений и процессов в природе и обществе чрезвычайно велико.
Можно рассчитать среднюю заработную плату работников той или иной профессиональной группы (шахтера, врача) и средний месячный доход, который приходится на одного жителя страны, среднюю себестоимость продукции по группе предприятий, выпускающих данный вид продукции, средняя используется при моделировании рисковых ситуаций в бизнесе и экономике, например, при формировании финансового портфеля, контроль за риском портфеля.
Средняя характеризует качественно однородные группы изучаемого явления. Например, средняя заработная плата отражает типичный уровень оплаты труда для данного вида работников. Средняя величина в этом случае является не просто обобщающей, но и типической характеристикой совокупности. В качестве типических характеристик средней величины используется не только для однородных, но и для неоднородных совокупностей. Например, если рассчитывается потребление крепких спиртных напитков на душу населения, то из всей совокупности населения можно исключить детей в возрасте 10 лет, не говоря о том, что и довольно значительная часть других возрастных групп не потребляет этот продукт.
Средняя величина ВВП на душу населения, средняя величина потребления различных групп товаров на человека и другие подобные величины представляют обобщающие характеристики государства как единой экономической системы и носят название системных средних. Системные средние могут служить обобщающими характеристиками не только разнородных пространственных, но и динамических систем.
В статистике используют различные виды (формы) средних величин. Наиболее часто применяются средние величины:
Средняя арифметическая; Средняя гармоническая; Средняя геометрическая; Средняя квадратическая.
Все виды средних, используемых в статистических исследованиях, подразделяются на две категории: 1) степенные средние; 2) структурные (позиционные) средние.
При расчете средней, важно уметь правильно выбрать среднюю. В настоящее время общепринятым является определение средней на основе определяющего свойства.
Понятие определяющего свойства иногда заменяется понятием определяющего показателя. На практике определить среднюю во многих случаях можно через соотношение средней, или ее логическую форму.
Общие правила, которыми следует руководствоваться при выборе вида степенной средней:
1. Формулируется цель, для которой рассчитывается средняя и дается понятие определяющего показателя.
2. Приводится аналитическое выражение определяющего показателя.
3. Обосновывается формула расчета средней степенной, исходя из того, что величина определяющего показателя не изменится при замене индивидуальных значений признака из отдельных единиц совокупности средней величины.
Широкое применение средних объясняется тем, они имеют ряд положительных свойств, делающих их незаметным инструментом анализа явлений и процессов в экономике.
Важнейшее свойство средней заключается в том, что она отражает то общее, что присуще всем единицам совокупности.
Сущность средней заключается в том, что в ней взаимопогашаются отклонения значений признака отельных единиц совокупности, обусловленных действием случайных факторов, и учитываются изменения, вызванные действием основных факторов. Это позволяет абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.
15. Расчёт и применение показателей вариации в статистическом исследовании.
Информация о средних уровнях исследуемых показателей обычно бывает недостаточной для глубокого анализа изучаемого процесса или явления. Необходимо также учитывать и вариацию значений отдельных единиц относительно средне, которая является важной характеристикой изучаемой совокупности.
Значительной вариацией, например, подвержены курсы акций, объемы спроса и предложения, процентные ставки в разные периоды.
Основными показателями, характеризующими вариацию являются: размах, дисперсия, среднее квадратичное отклонение и коэффициент вариации.
Размах вариации. Недостатком показателя является то, что он оценивает только границы варьирующего признака и не отражает его колеблемость внутри этих границ.
Дисперсия – лишена этого недостатка, рассчитывается как средний квадрат отклонений значения признака от их средней величины. Рассчитывается как по невзвешенной, так и по взвешенной форме.
Среднее квадратическое отклонение – определяется как квадратный корень на дисперсии и имеет ту же размерность, что и изучаемый признак.
Показатель вариации позволяет получить абсолютное значение вариации.
Коэффициент вариации – измеряет колеблемость в относительном выражении, относительно среднего уровня. Во многих случаях является более предпочтительным.
Информационность показателей вариации повышается, если они рассчитываются для целей сравнительного анализа. При этом показатели, рассчитанные для одной совокупности, сопоставляются с показателями, рассчитанными по другой аналогичной совокупности или по той же самой, но относящейся к другому периоду времени. Например, исследуется динамика вариации производственных страховых компаний выплат за ряд месяцев или лет.
Показатели вариации также являются составной частью или основной для расчетов других статистических показателей. Они используются в анализе взаимосвязей между признаками, в измерении структурных сдвигов в экономике, в оценке рисков (страхового, систематического на рынке ценных бумаг и прочее).
16. Средняя арифметическая величина и её расчёт, свойства средней арифметической.
Средняя величина – наиболее распространенная форма статистических показателей, представляет собой обобщенную характеристику признака в статистической совокупности. Средняя величина дает обобщенную характеристику однотипных явлений по одному из варьирующих признаков. Она отражает уровень этого признака, отнесенный к единой совокупности.
Средняя арифметическая величина относится к степенным средним: в зависимости от характера имеющихся данных может быть простой или взвешенной.
Средняя арифметическая простая – используется в тех случаях, когда расчет осуществляется по сгруппированным данным.
Средняя арифметическая взвешенная применяется в тех случаях, когда при расчете средних величин значения признака, могут повторяться, встречаться несколько раз.
В подобных случаях расчет средней производится по сгруппированным данным, или вариационным рядам, которые могут быть дискретными или непрерывными.
Свойства средней арифметической:
1. Произведение средней на сумму частот равно сумме произведений вариантов на соответствующие частоты.
2. Сумма отклонений индивидуальных значений признака от средней арифметической равно нулю.
3. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов от любой другой произвольной величины С.
4. Если все варианты уменьшить или увеличить на постоянное число А, то средняя арифметическая соответственно уменьшиться или увеличится на ту же величину.
5. Если все величины признака изменить в А раз, то средняя измениться в А раз.
17. Степенные средние. Правила мажорантности средних.
Категорию средней можно раскрыть через понятие определяющего его свойства. Согласно этому понятию средняя, являясь обобщающей характеристикой своей совокупности, должна ориентироваться на определенную величину, связанную со всеми единицами этой совокупности. Эту величину можно представить в виде функции: (х1,……..,хn) - определяющая функция.
Так как данная величина в большинстве случаев отражает реальную экономическую категорию, понятие определяющего свойства средней иногда заменяют понятием определяющего показателя. Если в приведенной выше функции все величины х1,…..,хn заменить средней величиной
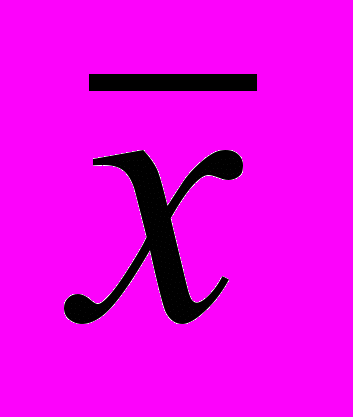, то значение этой функции должно остаться прежним: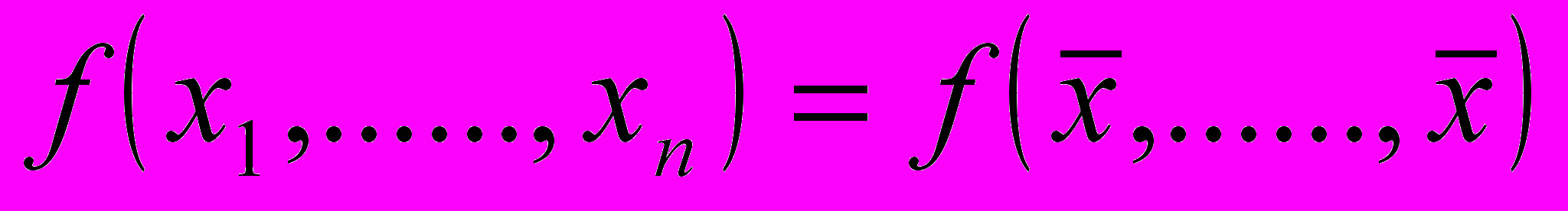
Исходя из этого равенства и определяется средняя.
Степенные средние получаются при решении выше приведенного уравнения, в котором функциональная связь единиц совокупности представлена степенной функцией. (k- показатель степенной функции):
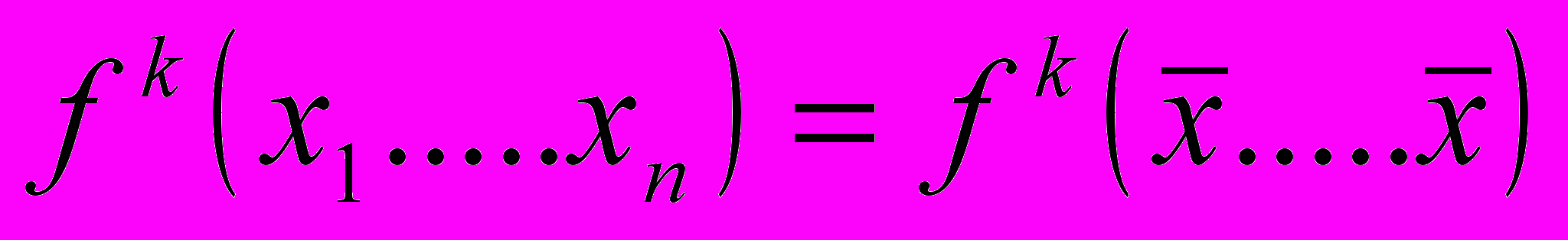
При значении k = -1 – получают среднюю гармоническую;
При k = 0 – среднюю геометрическую;
При k = 1 – среднюю арифметическую;
При k = 2 – средняя квадратическая.
В зависимости от исходной информации рассчитываются средние: простые или взвешенные.
Известно, что степенные средние разных видов, исчисленные по одной и той же совокупности, имеют разные количественные значения. И чем больше показатель степени k, тем больше и величина соответствующей средней:
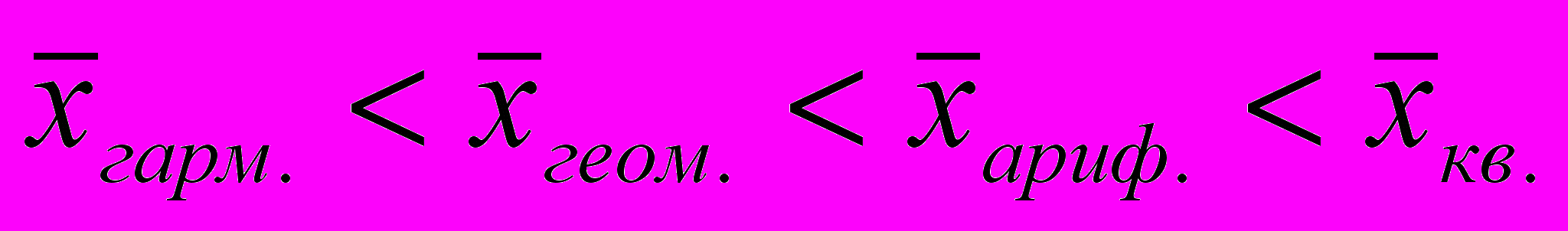
Это свойство степенных средних возрастать с повышением показателя степени определяющей функции называется мажорантностью средних.
18. Структурные средние (мода, медиана).
К средним величинам, кроме степенных средних, относят также моду и медиану (структурные средние).
Мода и медиана определяется лишь структурой распределения. Поэтому их именуют структурными позиционными средними.
Медиану и моду часто используют как среднюю характеристику в тех совокупностях, где расчет средней степенной невозможен или нецелесообразен.
Медиана – расположена в середине ранжированного ряда и делит его пополам.
С помощью медианы, таким образом, можно определить то значение признака, которое делит единиц ранжированного ряда ряда на две части.
Расчет медианы по не сгруппированным данным производится следующим образом:
1. Располагают индивидуальные значения признака в возрастающем порядке;
2. Определяется порядковый номер медианы по формуле, в зависимости от четности или нечетности числа индивидуальных признаков.
Мода – это наиболее часто встречающееся значение признака у единиц данной совокупности. Она соответствует определенному значению признака.
Медиану и моду можно определить графически. Медиана определяется по кумуляте распределения. Мода определяется по гистограмме распределения.
19. Организация проведения несплошного статистического наблюдения, его виды, условия, ошибки выборочного наблюдения при различных способах отбора.
В последнее время все более широкое распространение получают несплошные наблюдения, которые могут быть организованы как выборочные, способ основного массива и монографические.
При выборочном наблюдении обследованию подвергаются отобранные в определенном порядке часть единиц совокупности, а полученные результаты распространяются на всю совокупность.
Отбор производится таким образом, чтобы выборочная совокупность была репрезентативна, т.е. как можно точнее воспроизводила всю совокупность со всеми характерными для нее особенностями.
При использовании способа основного массива обследованию подлежат наиболее существенные крупные единицы, которые имеют максимальный удельный вес в совокупности. Такое наблюдение используется для получения данных о ценах на товары, реализуемые на рынках.
В отличие от выборки и способа основного массива, являющимися массовыми наблюдениями, при монографическом наблюдении тщательному наблюдению подвергаются отдельные единицы совокупности. Цель такого наблюдения – детальное описание каждой единицы, которое невозможно при описании массовых обследований. Монографическое описание можно использовать для характеристики отдельного предприятия, бюджета семьи и др.
Массовое и монографическое наблюдения дополняют друг друга.
Ошибки выборочного наблюдения при различных способах отбора. Различают:
1. Простую случайную выборку;
2. Типическую (районированная или стратифицированная) выборку;
3. Серийную (гнездовая) выборку;
4. Механическую выборку (предварительно упорядочение???);
5. Комбинированную выборку.
Общая величина возможной ошибки выборочной характеристики слагается из ошибки двоякого ряда: ошибок регистрации и ошибок репрезентации.
Для каждого конкретного выборочного наблюдения величина ошибки репрезентативности может быть определена по соответствующим формулам.
Простая случайная выборка (собственно случайный отбор) – определяет стандартную и предельную ошибку выборки:
1. Формулы расчета средней ошибки выборки при собственно случайном и механическом отборе (повторный и без повторный отбор);
2. Формулы расчета средней ошибки выборки при типическом отборе (повторный и без повторный отбор);
3. Формулы расчета выборки при серийном отборе (повторный и без повторный отбор).
Комбинированная выборка использует комбинации разных способов отбора. Ошибка такой выборки определяется ступенчатостью отбора.
20. Способы формирование выборочных совокупностей и распространение выборочных данных на генеральную совокупность.
Понятие генеральной и выборочной совокупности. Способы отбора единиц наблюдения из генеральной совокупности: повторный и бесповторный отбор, характеристика вероятности попадания каждой отдельной единицы в выборку при каждом способе отбора.
Классификация ошибок выборочного наблюдения: ошибки регистрации, ошибки наблюдения.
Методы (алгоритм) отбора единиц в выборочную совокупность.
Формы организации выборочного наблюдения: типическая (районированная или стратифицированная) выборка, серийная (гнездовая) выборка, механическая выборка, комбинированная выборка.
Методы распространения итогов выборочных наблюдений на генеральную совокупность: метод взвешивания, метод восстановления неответов. Характеристика неответов и способов их восстановления.
21. Предельная ошибка выборки. Доверительные коэффициенты.
Понятие средней и предельной ошибки выборки, коэффициента доверия, доверительных интервалов. Формулы расчеты средней и предельной ошибки выборки для повторного и бесповторного отбора.
22. Оценка параметров малых выборок. Критерий Стьюдента.
Критерий отнесения выборок к малым выборкам. Условия, при которых может быть использован закон Стьюдента. Формула расчета средней ошибки для малых выборок. Расчет предельной ошибки малой выборки с использованием таблиц Стьюдента.
23. Определение оптимальной численности выборки.
Взаимосвязь точности выборки и объема выборки. Формулы определения необходимой численности выборки при повторном и бесповторном отборе. Основные подходы определения вариации (дисперсии) изучаемого признака в генеральной совокупности: результаты обследования данного объекта в предыдущие периоды, результаты обследования аналогичных объектов, специально проведенное небольшое по объему выборочное обследование данного объекта с целью изучения вариации наблюдаемых признаков.
24. Основные принципы анализа взаимосвязей между общественными явлениями, виды взаимосвязей.
Понятие факторных и результативных признаков. Виды взаимосвязи между признаками: функциональные, статистические (стохастические), корреляционные. Классификация связи между явлениями и признаками: по степени тесноты, направлению, аналитическому выражению. Количественные критерии оценки тесноты связи. Понятие прямой и обратной связи. Линейные и нелинейные связи.
Основные задачи при исследовании корреляционных зависимостей между признаками: предварительный анализ свойств исследуемой совокупности единиц; установление факта наличия связи, определение ее направления и формы; измерение степени тесноты связи между признаками; построение регрессионной модели, т.е. нахождение аналитического выражения связи; оценка адекватности модели, ее экономическая интерпретация и практическое использование.
25. Классификация статистических методов исследования взаимосвязей.
Задачи корреляционного анализа. Методы выявления наличия связи, ее характера и направления: параллельное сопоставление рядов результативного и факторного признаков, графическое изображение фактических данных с помощью поля корреляции, построение групповых корреляционных таблиц, дисперсионный анализ.
Виды корреляционных зависимостей: парная корреляция, частная корреляция, множественная корреляция. Понятие и определение видов корреляционных зависимостей.
26. Изучение парных взаимосвязей с помощью аналитических группировок. Дисперсионный анализ.
Виды аналитических таблиц: простая аналитическая группировка, таблицы взаимной сопряженности, корреляционная «шахматная» таблица.
Группировка значение факторного и результативного признака: формула Стэрджеса для определения величины интервала.
Правило построения корреляционной таблицы: расположение факторного и результативного признаков, заполнение клеток «шахматной» таблицы.
Измерение тесноты связи на основе данных аналитических таблиц. Эмпирическое корреляционное отношение: порядок расчета и оценки, исходные данные для расчета (общая и межгрупповая дисперсии результативного признака).
27. Кореляционно - регрессионный анализ, показатели тесноты связи, коэффициенты Фехнера, линейная корреляция.
Понятие и задачи корреляционно-регрессионного анализа. Важнейшие условия применения методов корреляционно-регрессионного анализа.
Показатели, используемые для количественной характеристики тесноты связи: коэффициент корреляции знаков (коэффициент Фехнера), линейный коэффициент корреляции, коэффициент детерминации.
Пределы изменения коэффициента Фехнера и линейного коэффициента корреляции. Описание тесноты связи и ее направления с помощью коэффициента Фехнера и линейного коэффициента корреляции.
28. Сущность и назначение непараметрических методов изучения взаимосвязей. Коэффициенты ассоциации и контингенции.
Понятие и область применения непараметрических методов: измерение взаимосвязи между качественными признаками, измерение интенсивности связи между признаками, форма распределения которых отличается от нормального распределения.
Понятие ранга и процедуры ранжирования. Коэффициенты корреляции рангов для оценки тесноты связи: коэффициент Спирмена, коэффициент Кендэла, множественные коэффициенты ранговой корреляции (коэффициенты ассоциации и контингенции). Области применения коэффициентов.
29. Коэффициент взаимной сопряжённости признаков. Критерии К. Пирсона, А Чупрова для взаимосвязей качественных признаков.
Область применения коэффициентов взаимной сопряженности Пирсона и Чупрова (оценка наличия связи между качественными показателями с большим числом градаций). Критерий «хи- квадрат», используемый для расчета коэффициентов взаимной сопряженности Пирсона и Чупрова.
30. Ранговая корреляция, коэффициент корреляции рангов Спирмена.
Порядок ранжирования признаков. Правило присваивания рангов для признаков, имеющих равное значение. Порядок расчета коэффициента Спирмена. Пределы изменения коэффициента Спирмена. Прямая и обратная связь. Значения показателя, характеризующего прямую и обратную связь.
31. Статистическая практика применения аналитических показателей рядов динамики.
Назначение рядов динамики (выявление и отображение процесса развития и изменения социально-экономических явлений во времени). Основные элементы ряда динамики: показатели уровня ряда, показатели времени (годы, кварталы, месяцы, сутки), показатели момента времени.
Классификация рядов динамики: в зависимости от способа выражения уровней ряда (ряды абсолютных, относительных и средних величин, примеры из статистической практики), в зависимости от характера отображения времени (интервальные и моментные ряды, отличительные особенности интервальных и моментных рядов динамики, накопленные итоги для интервальных рядов, примеры из статистической практики), в зависимости от расстояния между уровнями рядов динамики ( с равноотстоящими уровнями и неравноотстоящими уровнями во времени, примеры из статистической практики).
Аналитические показатели для анализа скорости и интенсивности развития явления (абсолютный прирост, темп роста, темп прироста, примеры из статистической практики).
32. Основные правила построения рядов динамики. Значение и способы привидения рядов динамики к сопоставимому виду.
Важнейшие принципы и правила построения ряда динамика. Проблема сопоставимости данных, основные причины несопоставимости уровней ряда динамики: изменение единиц измерения и единиц счета, методология учета или расчета показателей, периодизация динамики, изменение круга охватываемых объектов, изменение территориальных границ.
Методы приведения уровней ряда к сопоставимому виду: метод смыкания рядов, метод приведения к одному основанию.
33. Важнейшие статистические характеристики ряда динамики. Средние величины в рядах динамики.
Система абсолютных и относительных показателей: абсолютный прирост, коэффициент роста, темп роста, темп прироста, абсолютное значение одного процента прироста. Показатели динамики с постоянной базой (базисные показатели), показатели динамики с переменной базой (цепные показатели). Взаимосвязь показателей, вычисленных с постоянной и переменной базой.
Средние показатели динамики: средние уровни ряда, средние показатели изменений уровня ряда. Исчисление среднего уровня в интервальных и моментных рядах. Средняя хронологическая простая и взвешенная: формулы для вычисления, условия применения простой или взвешенной средней. Средний коэффициент роста, средний темп роста, средний темп прироста: формулы для вычисления, условия применения простой или взвешенной средней.
34. Статистические методы выявления основной тенденции развития исследуемого явления.
Важнейшие составляющие колеблемости уровней временного ряда: тренд, сезонный и случайный компоненты.
Основные группы методов анализа основной тенденции в рядах динамики: сглаживание или механическое выравнивание отдельных членов ряда динамики с использованием фактических значений соседних уровней; выравнивание с применением кривой, проведенной между конкретными уровнями ряда таким образом, чтобы она отображала тенденцию, присущую ряду, и одновременно освобождала его от незначительных колебаний.
Метод укрупненных интервалов, метод скользящей средней: практическое использование, преимущества и недостатки методов. Аналитическое выравнивание: признаки, которыми нужно руководствоваться при выборе формы кривой. Аналитическое выравнивание ряда динамики по прямой. Метод наименьших квадратов как способ определения параметров уравнения.
35. Применение статистических методов прогнозирования социально-экономических явлений.
Понятие экстраполяции: перспективная, ретроспективная. Методы экстраполяции: среднего абсолютного прироста, среднего темпа роста, экстраполяция на основе применения метода наименьших квадратов к динамическому ряду и представление развития явление во времени в виде уравнения тренда, т.е. математической функции уровней ряда (y) от фактора времени (t). Условия применения каждого метода.
Понятие интерполяции. Методы интерполяции: среднего абсолютного прироста, среднего темпа роста, с помощью аналитического выравнивания.
36. Внутригодовые колебания и методы их анализа.
Понятие «сезонных колебаний» или «сезонной волны». Определение наличия сезонности, численное выражение проявления сезонных колебаний и выявления их силы и характера в различных фазах годового цикла. Характеристика факторов, вызывающих сезонные колебания. Оценка последствий, к которым приводит наличие сезонных колебаний. Математическое моделирование сезонности.
Методы измерения сезонных колебаний: метод абсолютных разностей; метод относительных разностей; построение индексов сезонности. Определение индекса сезонности и порядок его расчета.
37. Ряды индексов с постоянными и переменными весами, с постоянной и переменной базой сравнения, их значение в статистическом анализе социально-экономических явлений.
Понятие системы индексов. Система базисных и система цепных индексов для индивидуальных и агрегатных индексов. Виды взаимосвязи между цепными и базисными индексами. Цепной метод для исчисления агрегатных индексов: область применения метода Система индексов с постоянными весами. Система индексов с переменными весами. Индексы –дефляторы.
38. Индексный метод в экономических исследованиях: теория, виды и практические расчёты.
Понятие индекса. Задачи, решаемые с помощью индексного метода: характеристика общего изменения сложного социально-экономического явления; анализ влияния каждого фактора на изменение индексируемой величины путем исключения воздействия прочих факторов; анализ влияния структурных факторов на изменение индексируемой величины
Индивидуальные, сводные (агрегатные) индексы. Системы индексов для неоднородной совокупности: индексы Ласпейреса, индексы Паше. «Идеальная» формула Фишера
Индекс потребительских цен: определение, формула для расчета, порядок организации статистических наблюдений для формирования исходной информации. Расчет сводных (агрегатных) индексов на основе индивидуальных индексов: средние арифметические и средние гармонические индексы.
39. Основные принципы построения и использования в экономическом анализе многофакторных индексных моделей.
Многофакторные модели (мультипликативные, аддитивные). Последовательность в записи фактов при построении мультипликативных моделей Понятие качественных и количественных факторов. Применяемые на практике правила построения индексов качественных и количественных показателей. Изучение влияния факторных признаков на абсолютный прирост результирующего признака.
40. Индексный метод измерения факторов, влияющих на изменение среднего уровня признака и их практическое применение.
Понятие однородных и не однородных совокупностей. Индексы переменного состава, фиксированного состава и структурных сдвигов. Взаимосвязь индексов. Разложение абсолютных приростов по факторам. Использование индексов для экономического анализа (индекс средней себестоимости, индекс средней цены, индекс средней урожайности).