Освоивших образовательные программы основного общего образования, организуемой территориальными экзаменационными комиссиями Калининградской области в 2008-2009 учебном году Калининград
| Вид материала | Методические рекомендации |
- Администрация владимирской области департамент образования прика, 401.39kb.
- Прика з, 165.18kb.
- Калужская область, 207.13kb.
- Приказ 23. 09. 2010 №2447 г. Саратов, 2042.38kb.
- Аналитическая справка по итогам проведения государственной (итоговой) аттестации обучающихся,, 1088.56kb.
- Верховного Совета Российской Федерации, 1992, n 30, ст. 1797; Собрание закон, 85.26kb.
- Инструктивно-методическое письмо «О преподавании русского языка в общеобразовательных, 2788.3kb.
- Публичный доклад, 1564.51kb.
- Целевая программа калининградской области «Содействие занятости населения Калининградской, 635.09kb.
- Программа подготовки выпускников 9-х классов моу «Октябрьская средняя общеобразовательная, 421.48kb.
Анализ результатов выполнения заданий первой части экзаменационной работы
Первая (тестовая) часть работы содержит 16 заданий, проверяющих математическую подготовку выпускников основной школы на базовом уровне.
Распределение заданий первой части работы представлена в таблице:
Таблица 7
| № п/п | Раздел содержания | Число заданий |
| 1 | Числа | 3 |
| 2 | Буквенные выражения | 2 |
| 3 | Преобразования алгебраических выражений | 3 |
| 4 | Уравнения | 3 |
| 5 | Неравенства | 2 |
| 6 | Последовательности и прогрессии | 1 |
| 7 | Функции и графики | 2 |
Распределение заданий первой части работы по видам познавательной деятельности:
Таблица 8
| Познавательная категория | Число заданий |
| Умение применять известный алгоритм | 6 |
| Умение решить математическую задачу | 3 |
| Применение знаний в практической ситуации | 2 |
| Знание/понимание | 4 |
Общая картина решаемости выпускниками 9-х классов заданий первой части представлена в диаграмме 3:
Диаграмма 3
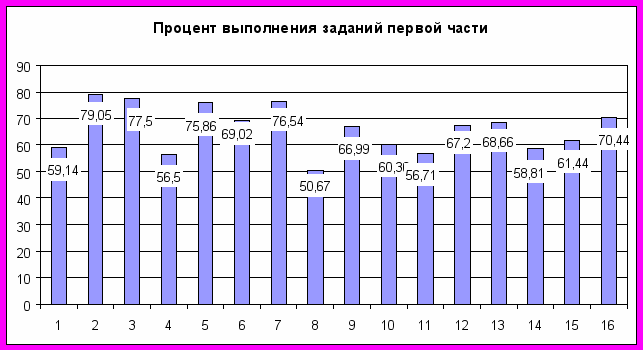
Предполагаемый процент верных ответов находится в диапазоне от 60% до 90%.
Таблица 9
| № п/п | Раздел содержания | Выполнили верно ( в среднем, %) | Диапазон выполнения ( в %) |
| 1 | Запись чисел в стандартном виде | 59,14 | 47,37 - 100 |
| 2 | Решение задач на процентные вычисления | 79,05 | 56,36 - 100 |
| 3 | Арифметические действия с положительными и отрицательными числами | 77,5 | 65,82 - 97,44 |
| 4 | Числовые подстановки в буквенные выражения | 56,5 | 39,91-94,12 |
| 5 | Выражение из формул одних величин через другие | 75,86 | 59,87-100 |
| 6 | Свойства квадратных корней и их применение в вычислениях | 69,02 | 58,55-100 |
| 7 | Алгебраические дроби. Сокращение дробей | 76,54 | 58,91-100 |
| 8 | Сложение, вычитание и умножение многочленов, формулы сокращенного умножения, преобразование целых выражений | 50,67 | 29,58-92,59 |
| 9 | Квадратное уравнение | 66,99 | 51,17-96,3 |
| 10 | Графическая интерпретация решения системы уравнений с двумя переменными | 60,36 | 39,44-82,78 |
| 11 | Переход от словесной формулировки соотношений между величинами к алгебраической. Решение текстовых задач алгебраическим способом | 56,71 | 44,73-89,74 |
| 12 | Арифметическая прогрессия. | 67,2 | 41,18-89,74 |
| 13 | Линейные неравенства с одной переменной | 68,66 | 53,95-89,66 |
| 14 | Квадратные неравенства с одной переменной | 58,81 | 26,47-67,86 |
| 15 | Квадратичная функция, ее свойства и график; парабола | 61,44 | 44,36-89,2 |
| 16 | Примеры графиков зависимостей, отражающих реальные процессы; чтение и интерпретация | 70,44 | 50,7-82,05 |
Анализируя данные, приведенные в таблице 11, можно прийти к выводу, что результаты выполнения одного и того же задания по территориям значительно различаются, поэтому в таблицах приводится и средний процент, и разброс по муниципалитетам.
Низкий результат выполнения первого задания связан с продолжением начатой в предыдущие годы линией работы с представлением реальных данных в стандартном виде. Учащиеся показали слабые умения пользоваться эквивалентными представлениями чисел, так более 50% девятиклассников не сумели перейти к записи числа в стандартном виде. Самый низкий процент выполнения этого задания относится к записи числа 9970 тыс. км2 в виде
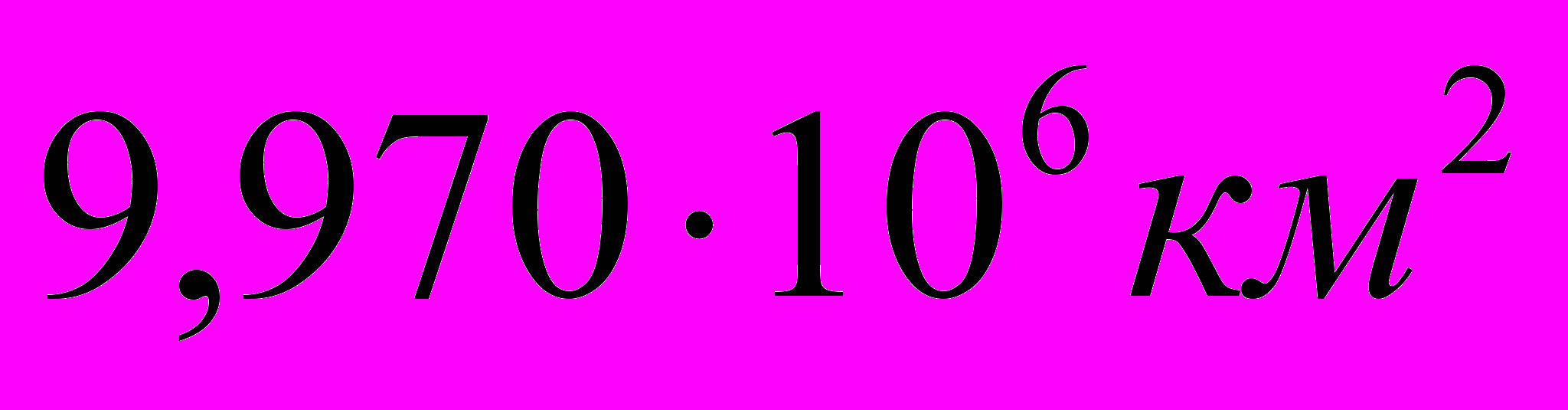, легче всего это было сделать учащимся для числа 510 млн. км2. Невысокие результаты можно объяснить тем, что на уроках математики учащиеся редко работают с данными, представленными в стандартном виде, чаще всего они встречают их на уроках физики, химии, биологии. Низкий процент выполнения данного задания говорит о неумении учащихся интегрировать свои знания. Сложным оказалось и выполнение арифметических действий в процессе подстановки числового значения в буквенное выражение (4 задание) для 60,09% учеников. Квадратный корень из чисел 0,25 и 0,36 извлекают с меньшим количеством ошибок, чем из дробей 0,04 и 0,09; значение алгебраической дроби находят точнее, чем разность дробей.
Как и в предыдущие годы для большинства учащихся остается сложным применить алгоритм преобразования целого выражения с привлечением формул сокращенного выражения и правил раскрытия скобок: до 70, 42 % учащихся не могут выполнить это задание (№ 8) без ошибок. На изучение данного материала выделяется достаточно большое время, уровень требований в учебном процессе достаточно высок, а результаты - низкие. Необходимо пересмотреть методические подходы к данному разделу алгебры, изучение должно строиться дифференцированно.
Задание 10: вычислить координаты точки пересечения двух прямых с помощью составления и решения системы двух линейных уравнений с двумя переменными, не могут решить до 60, 56 % девятиклассников. Базовую, стандартную задачу, присутствующую во всех учебниках и традиционно включаемую в итоговый контроль.
Низкие результаты наблюдаются и при переходе учащимися от словесной формулировки задачи (№ 11) к ее алгебраической модели - уравнению, 55,27 % девятиклассников не справились с заданием. Главная причина – в неумении понять задание и адекватно ответить на вопрос задачи. Низкий уровень умений осознанного чтения – одна из главных проблем в подготовке выпускников начальной школы, с которой сталкиваются многие учителя, работающие в пятых классах. Отсутствие целенаправленной работы по развитию этих умений в основной школе приводит к неуспешности школьников при выполнении заданий на основе анализа текста. Необходимо усиление внимания к осознанной работе с текстами.
Единственное задание на соотнесение - 14. До 73,53 % учеников не смогли соотнести квадратное неравенство с одной переменной с множеством его решений. Возможная причина - неумение применять метод интервалов к решению этого вида неравенств, в силу того, что данный способ воспринимается учащимися формально. Необходимо решать эти неравенства на основании графического представления - основным для девятиклассников методом: с помощью графика квадратичной функции.
От 10,8 % до 55,64 % выпускников основной школы не обладают навыками восприятия готового графика как целостного объекта с характерными свойствами, что будет существенно мешать содержательному овладению началами математического анализа в старших классах. Следует заметить, что перенос знания учащимися на аналогичную, но все же новую ситуацию затруднен, что бывает в случае ориентировки учащихся не на существенные, основополагающие отношения, а на внешние, ситуативные.
Больше половины учащихся показали неумение перейти с одного математического языка на другой при решении задачи на прогрессию, что говорит о непонимании содержательного смысла индексного обозначения. Необходимо заметить, что у выпускников часто возникают трудности, когда требуется перейти с одного математического языка на другой, когда речь идет о некоторой интерпретации. Это, безусловно, указывает, на проблемные места в математической подготовке школьников.
Что касается других заданий, то в целом проценты их верного выполнения находятся в прогнозируемых диапазонах.
Следует оценить положительные изменения в решении задачи с реальным сюжетом, связанной с выполнением несложных процентных расчетов. Причем, чем короче формулировка задачи, тем выше процент ее выполнения. Меньше стали ошибаться ученики и при выполнении арифметических действий с положительными и отрицательными числами, в выражении из формул одних величин через другие. На 14,24 % меньше ошибаются девятиклассники при выводе переменной величины, стоящей в числителе дроби, чем при выражении величины, стоящей в знаменателе. Меньше трети учащихся ошиблись в выполнении задачи, описывающей реальную ситуацию оплаты телефонных разговоров. Вообще, учащиеся лучше справляются с заданиями с выбором ответа, чем с заданиями, в которых требуется привести развернутый ответ.
Сравнивая результаты выполнения заданий первой части, можно отметить следующее: высокие результаты - 100% успеваемость показали учащиеся Янтарного, Светлогорского, Неманского и Ладушкинского муниципальных районов. Высокий процент успеваемости показали и учащиеся Озерского района - 97,73. Самый высокий показатель результатов экзамена в Черняховском ГОУ КО индустриально-педагогическом колледже: средний балл 4,18, качество знаний 85,7%. Наиболее стабильные результаты в Ладушкинском ГО: 82,35% учащихся подтвердили свои знания, 11,76% повысили и 5,88% понизили. Можно сделать вывод, что учащиеся данных муниципалитетов прошли психологическую адаптацию к итоговой аттестации. Несомненно, этому способствовал и тот факт, что учащиеся эти районов приняли участие в «репетиционном» экзамене.
В Калининграде больше всего учащихся, принявших участие в ГИА в новой форме - 2832 (44,53%) . Средний балл 3,27, процент успеваемости 76,24, качество знаний 39,94%. Лучшие результаты в МОУ лицей № 23,самый низкий показатель результатов в ГОУ школа - интернат № 3.
Среди учащихся, набравших максимальный балл 65% из школ повышенного уровня, 35% - из общеобразовательных школ.
Выполнение заданий по вариантам (в %).
Таблица 10
| № задания | 919 вариант | 920 вариант | 921 вариант | 922 вариант |
| 1 | 60,98 | 66,75 | 45,41 | 63,11 |
| 2 | 75,16 | 78,11 | 86,19 | 76,69 |
| 3 | 78,73 | 78,42 | 77,45 | 75,24 |
| 4 | 57,59 | 68,19 | 55,48 | 44,54 |
| 5 | 69,32 | 83,56 | 70,49 | 79,91 |
| 6 | 64,55 | 68,57 | 70,17 | 72,65 |
| 7 | 77,85 | 75,91 | 76,69 | 75,55 |
| 8 | 52,2 | 53,14 | 50,92 | 46,43 |
| 9 | 62,17 | 70,08 | 68,02 | 67,53 |
| 10 | 62,3 | 60,41 | 60,29 | 58,43 |
| 11 | 53,89 | 57,28 | 58,07 | 57,61 |
| 12 | 63,49 | 68,82 | 70,68 | 65,63 |
| 13 | 70,83 | 69,76 | 65,04 | 69,05 |
| 14 | 58,85 | 58,41 | 60,16 | 57,8 |
| 15 | 60,04 | 66,56 | 65,55 | 53,63 |
| 16 | 64,81 | 70,83 | 75,81 | 70,31 |
Девятиклассники лучше справились с заданиями 920 варианта, немного хуже с задачами 922. Можно утверждать, что вопрос в одном из вариантов оказался немного более простым, а в другом сложнее. Хотя нет ситуаций, когда в том или другом варианте правильно ответили бы на вопрос вдвое больше учащихся в сравнении с результатами выполнения других вариантов. Приходится констатировать, что при решении большинства задач учащиеся оказались в равных условиях.
Анализ результатов выполнения заданий второй части экзаменационной работы.
Назначение второй части экзаменационной работы дифференцированная проверка повышенного уровня учебных достижений выпускников основной школы. Ниже в таблице 12 представлены результаты выполнения заданий, которые, как и в прошлом году представляют следующие блоки содержания: выражения и их преобразования, уравнения и системы уравнений, неравенства, координаты и графики, геометрическая прогрессия.
Новым можно считать задание № 20 исследовательского характера, которое не встречается в учебниках по алгебре, но присутствует во всех учебных изданиях, рекомендуемых ФИПИ для подготовки к экзамену. Идея его решения также приводилось в методическом письме «Об использовании результатов государственной (итоговой) аттестации выпускников основной школы в новой форме в 2008 году в преподавании алгебры в общеобразовательных учреждениях»:
«П р и м е р 2. Имеет ли произведение ab, где b = 5 – a, наибольшее значение, и если имеет, то при каких а и b оно достигается?
Подставив в произведение ab вместо b разность 5 – a, получим:
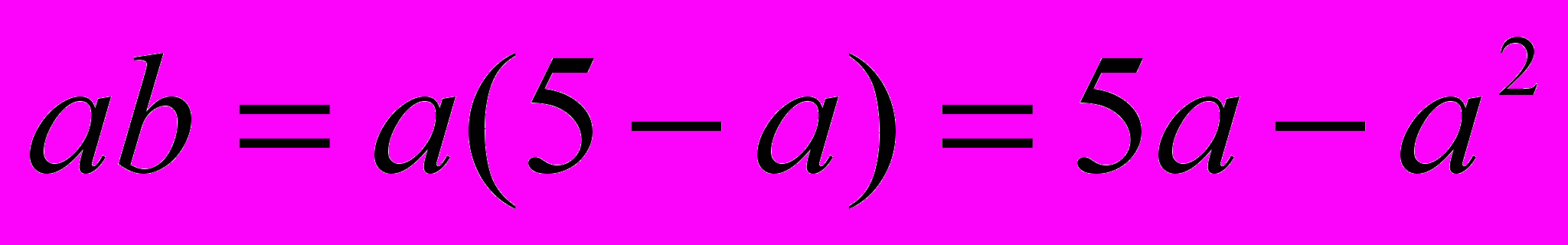. Теперь надо исследовать квадратный трехчлен 
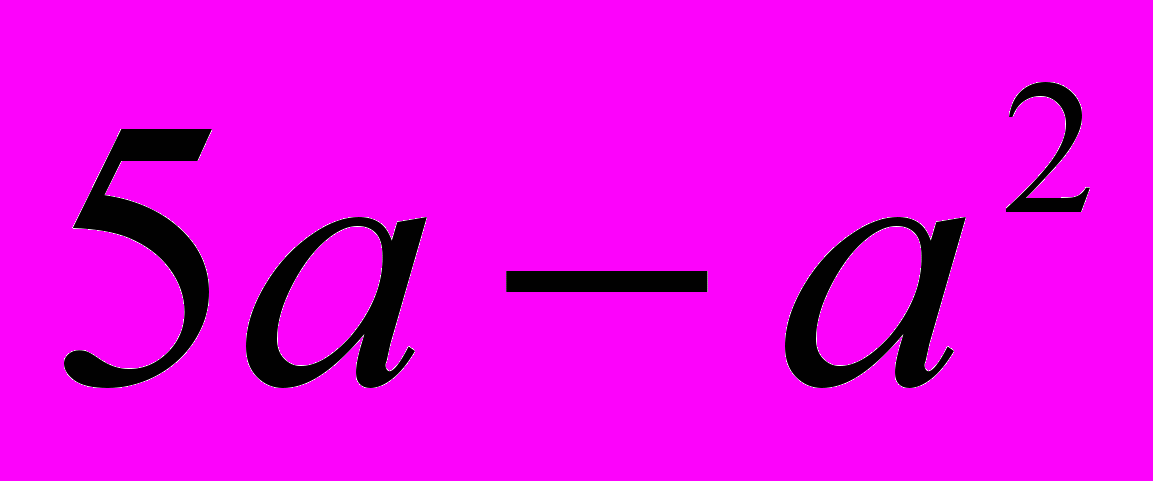. Воспользуемся свойствами квадратичной функции. Ее график – парабола. Коэффициент при а2 отрицателен, поэтому ветви параболы направлены вниз, и функция имеет наибольшее значение.Так как корни трехчлена – числа 0 и 5, то абсцисса вершины параболы равна 2,5. Таким образом, наибольшее значение трехчлен
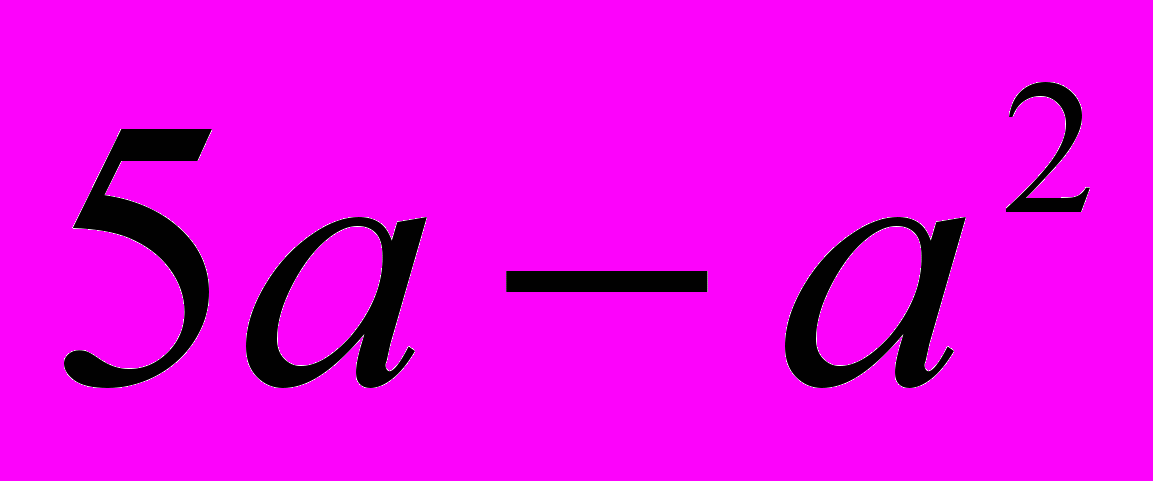, а, значит, и произведение ab, принимает при а = 2,5. Найдем соответствующее значение b: 
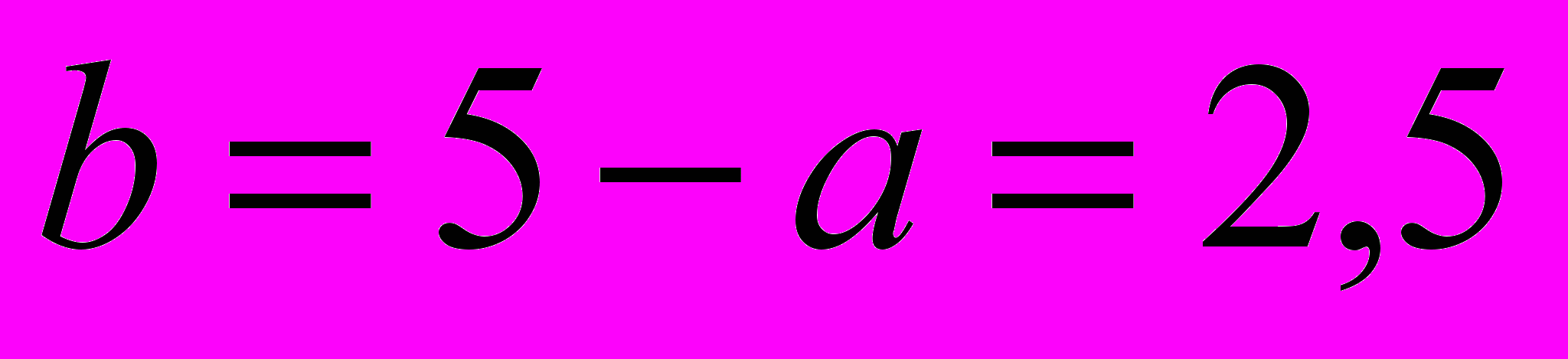. Ответ: имеет; при а = b = 2,5.» Из 514 отличников 356 человек не справились с заданием № 20, 41 учащийся набрал по 1 баллу, 17 - 2 балла, 27 - 3 балла и 73 учащихся выполнили его верно.
Как и для части 1, в таблице приводится не средний процент, а разброс по муниципалитетам. Примечательно, что процент верного выполнения заданий практически никогда не превышает прогнозируемого.
Результаты выполнения заданий второй части
| № п/п | Содержание заданий | Уровень (количество баллов) | Верно выполнили (%) | Планируемая трудность (%) |
| 17 | Решение рациональных уравнений высших степеней | 2 | 13,82-61,54 | 40-60% |
| 18 | Исследование линейного неравенства | 3 | 1,82-39,93 | 20-40% |
| 19 | Геометрическая прогрессия. Формулы общего члена геометрической прогрессии | 3 | 0-44,83 | 20-40% |
| 20 | Исследование целого выражения. Функция, область значений функции | 4 | 0-13,79 | 8-20% |
| 21 | Аналитическая запись функции | 4 | 0-10,34 | 8-20% |
Стандартное задание «Решите уравнение» третьей степени можно считать выполненным успешно. Основными ошибками учащихся были неверное разложение на множители способом группировки. Ошибки и в решении неполного квадратного уравнения.
18 задание является стандартным заданием повышенного уровня сложности. Сложность заключалась в присутствии иррационального множителя, сбившего с толку учащихся, и решавших неравенство методом интервалов. Ошибки из-за несформированности базовых умений: сравнение значений числовых выражений, содержащих квадратные корни. Как уже отмечалось при анализе выполнения первой части экзаменационной работы, учащиеся всегда затрудняются при интерпретации, применении знаний. В данном случае надо было, прежде всего, распознать в первом множителе иррациональное число и, определив его знак, решить линейное неравенство.
Задание №19 - задача, решаемая алгебраическим методом. Можно считать результат удовлетворительным, он попадает в диапазон прогнозируемых результатов. Ошибки при составлении системы уравнений и ее решении Фактические знания, требуемые для ее решения, не выходят за рамки обязательного минимума содержания, но чтобы решить ее, надо свободно владеть этими знаниями и уметь применить их в нужной ситуации.
Интересное задание исследовательского характера - №20, решение которого несложное и недлинное, но способно продемонстрировать алгебраическую культуру учащихся. Любое отклонение от привычных формулировок приводит к тому, что учащиеся не узнают стандартных заданий, не понимают смысла поставленных вопросов. Ведь основная «изюминка» данной задачи – это логический шаг: выразить одну переменную через другую, составить квадратичную функцию и определить ее наибольшее значение. Этот логический прием имеет общий характер и применяется при решении многих задач повышенного уровня, и обучение математике обязано формировать у сильных учащихся соответствующее умение. Никакими специальными приемами для решения подобной задачи владеть не надо, все необходимые фактические знания учащиеся получают в общем курсе алгебры основной школы. В силу этого такая задача имеет право на существование, а ее результаты указывают некоторое направление совершенствования преподавания. Примечательно, что процент верного выполнения задания не превышает прогнозируемого
Последнее сложное задание под силу учащимся классов с углублённым изучением математики. И процент выполнения до 10,34% вполне согласуется с этим утверждением. Многие из приступивших не смогли найти продуктивный способ решения. И, конечно, явная недостаточность или погрешности в пояснениях своих действий. Учащиеся правильно определяли уравнения прямых, но допускали ошибки в определении соответствующих им промежутков. Вся суть этой задачи – во втором этапе, требующем проведения некоторого исследования.
Методические рекомендации по подготовке к государственной (итоговой) аттестации выпускников IX классов общеобразовательных учреждений
(в новой форме) по алгебре
Одной из важных целей обучения математике является формирование умения ясно, точно, логически грамотно выражать свои мысли, как в устной, так и в письменной форме. Однако цель эта достигается далеко не всегда. Так, работы учащихся свидетельствуют об отсутствии у них общих представлений о том, что собственно нужно указывать и комментировать в ходе решения той или иной задачи, какие моменты решения действительно являются существенными. Очень часто встречается словесное описание применяемых алгоритмов. И, напротив, нечасто встречаются работы, в которых используются такие слова, раскрывающие логику рассуждений, как «следовательно», «поэтому», «значит» и пр. недостатком в записи решения является неверное употребление математической терминологии и символики. Так, вместо слов «решим неравенство», ученики часто пишут «решим уравнение», вместо словосочетания «найдем корни квадратного трехчлена» можно увидеть выражение «решим квадратный трехчлен»; «определим знак скобки», вместо «определим знак множителя». Можно встретить такое ошибочное выражение, как «график прямой». Серьезное непонимание проявляется в неуместном употреблении логических союзов «И» и «ИЛИ». В сознании учащихся наблюдается путаница между употреблением этих союзов как логических связок и как частей речи русского языка. Например, результат решения квадратного уравнения может быть записан разными способами, например:
, 
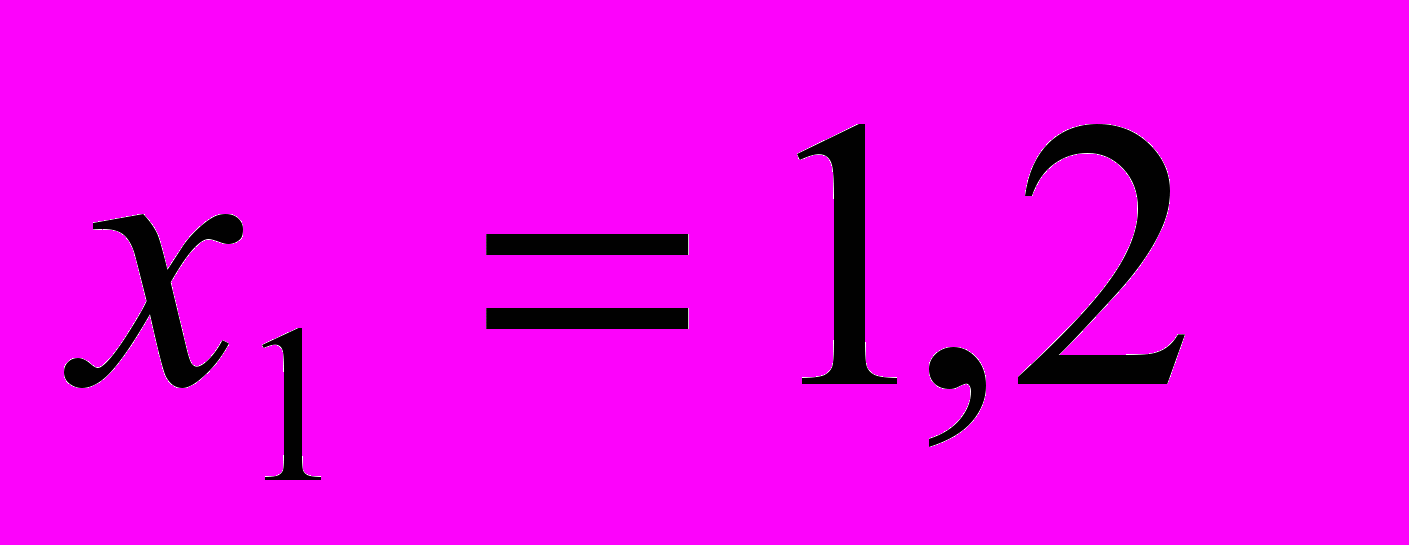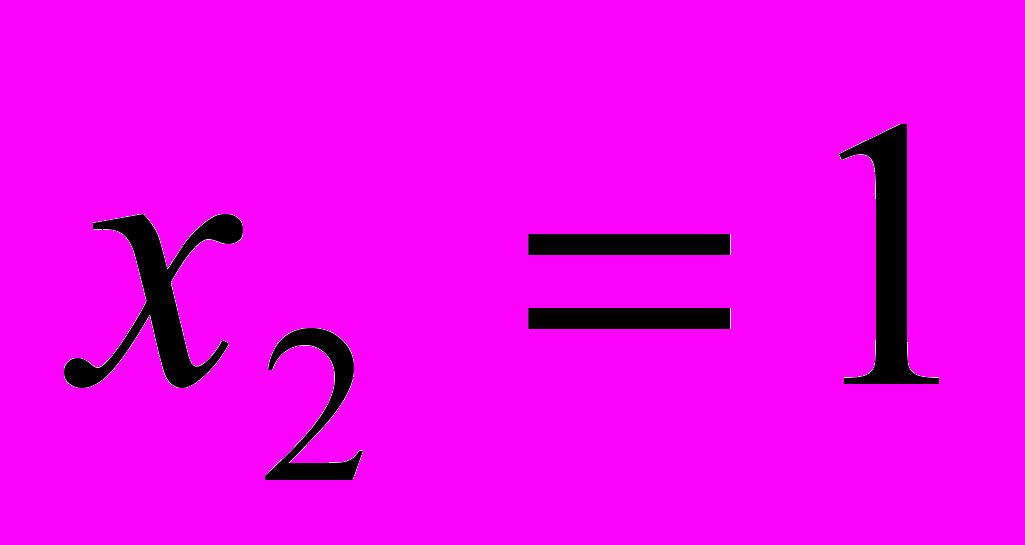; 1,2 и 1; 1,2; 1, но не х. = 1,2 или х=1. Учащиеся, выполняющие задания второй части работы, т.е. относящиеся к хорошо успевающим школьникам, не вооружены элементарными техническими навыками, своего рода азбукой преобразований, которая облегчает выполнение выкладок, позволяет избежать случайных ошибок.Особенность подготовки троечников к экзамену состоит в том, что они освоили на базовом уровне алгоритмические умения, но имеют существенные пробелы в понятийной стороне. При подготовке таких учащихся целесообразно нацеливать на безошибочное выполнение первой части, правильно расставляя акценты и учитывая их реальные возможности. Учителю необходимо ставить перед учащимся ту задачу, которую он может реализовать. Больше обращать внимание на задачи категории «знание/понимание», но не в ущерб алгоритмическим. Напоминать, что включенные в работу задания необходимо выполнять в основном письменно, используя для этого черновик. Решение должно быть записано аккуратно и с достаточной степенью подробности, чтобы ученик не допускал досадных ошибок технического характера. Наличие в первой части работы большого числа заданий с выбором ответа, где из четырех предложенных ответов только один верный, не означает, что верный ответ нужно угадывать, подбирать и т.д.
Более сильных учащихся можно нацеливать на то, что иногда анализ предложенных ответов помогает сразу увидеть верный, и этим есть смысл пользоваться. Некоторые виды заданий рассчитаны на то, что ученик найдет короткий способ решения, опираясь на известные факты. Важнейшим условием успешности выполнения заданий является осмысленность, осознанность действий ученика и просто здравый смысл. В противном случае, даже имея необходимые знания, можно прийти к неверному ответу. Вообще привычка к самоконтролю, к самопроверке для учащихся не менее важна, чем знание правил и формул. Всегда полезно проверить себя, используя тот или иной подходящий в данной ситуации прием.
Представленный выше анализ результатов содержит достаточное количество прямых и косвенных рекомендаций, позволяющих увидеть слабые места в подготовке учащихся и наметить пути совершенствования учебного процесса, как в целом, так и при работе со школьниками, имеющими разный уровень подготовки и разные потребности в математике.
С целью совершенствования государственной (итоговой) аттестации выпускников IX классов необходимо:
- учитывать стрессовую ситуацию экзамена и спланировать работу по его проведению так, чтобы создать оптимальные условия для психологической адаптации подростков к итоговой аттестации;
- в каждом образовательном учреждении провести анализ результатов ГИА 2009 года по математике и спланировать работу методического объединения образовательного учреждения уже в начале учебного года;
- выявлять пробелы в знаниях и умениях учащихся посредством мониторинга базового уровня освоения программного материала; оперативно проводить коррекционные мероприятия: разного рода консультации, обучающие самостоятельные работы, использование специально разработанных систем упражнений с учётом причин возникновения пробелов и т.п.; корректировать рабочие программы с учётом «проблемных тем»;
- предусмотреть использование различного задачного материала, где применяются идеи варьирования исходных данных задачи, нестандартная постановка вопросов, используются различные трактовки понятий и т.п.; при обучении решению задач повышенного уровня сложности особое внимание следует уделить именно обучению процессу поиска различного числа решений;
- учитывать принципиальную возможность включения в экзамен заданий вероятностно-статистической линии и развивать у школьников умение работать с информацией, представленной в различной форме (текст, график, таблица, диаграмма и т.п.), уделяя значительное внимание ситуациям из реальной практики.
- пересмотреть методы, приёмы и средства, применяемые при изучении содержательной линии «Функции и графики»;
- использовать педагогический потенциал педагогов ОУ, показавших высокий уровень подготовки школьников к итоговой аттестации.
ГЕОГРАФИЯ
Анализ выполнения экзаменационной работы по географии в 2008/2009 учебном году
Выпускной экзамен по предмету «География» в IX классах общеобразовательных учреждений в рамках государственной (итоговой) аттестации, проводился в два этапа 5 и 9 июня 2009 года, кроме этого дополнительно был выделен резервный день для тех учащихся кто не смог по уважительной причине сдать экзамен в установленные дни. В нём приняли участие выпускники 9-х классов в количестве 107 человек из семи муниципальных образований области.
Анализ результата экзамена дает возможность получить информацию о сильных и слабых сторон их подготовки учащихся по предмету, определить уровень усвоения знаний и умений отдельными группами выпускников, т.е. предоставляет данные, являющиеся необходимым условием реализации обратной связи в процессе обучения географии, и позволяет сформулировать рекомендации по совершенствованию процесса обучения в целях обеспечения более полного соответствия уровня подготовки выпускников требованиям государственного стандарта основного общего образования. Новая форма проведения экзамена позволяет сделать процедуру оценивания учебных достижений школьников открытой и объективной, обеспечить высокую дифференцируемость результатов.
Содержание экзаменационной работы определялось на основе следующих документов:
1) Обязательный минимум содержания основного общего образования по географии (приложение к Приказу Минобразования России от 19.05. 1998 г. №1236 « об утверждении временных требований к обязательному минимуму содержания основного общего образования»).
2) Федеральный компонент государственного стандарта основного общего образования (Приказ Минобразования России от 05. 03.2004 г. №1089 « Об утверждении федерального компонента государственных образовательных стандартов, основного общего и среднего (полного) общего образования») в соответствии с зафиксированными в нем требованиями к уровню подготовки выпускников. Структура работы в 2008/2009 учебном году и её содержание определялись «Спецификацией экзаменационной работы для проведения государственной итоговой аттестации выпускников IX классов общеобразовательных учреждений 2009 г. (в новой форме) по географии».
Калининградской области для проведения государственной (итоговой) аттестации девятиклассников использовались восемь вариантов экзаменационной работы: №№ 945-948;953-956.
На выполнение всей работы отводилось 120 минут. Оценивание результатов выполнения экзаменационной работы учащимися производилось специально созданными предметными комиссиями по географии из числа квалифицированных и прошедших обучение учителей географии. Отметки по 5-балльной шкале рекомендовалось выставлять в зависимости от общего количества балов (первичный балл), полученных выпускниками за выполнение всех заданий экзаменационной работы. При пересчете первичных баллов в отметку по 5-бальной шкале рекомендовалось использовать следующую схему:
Шкала пересчета первичного бала за выполнение экзаменационной работы в отметку по пятибалльной шкале