М. В. Лычагин Зав кафедрой д э. н., профессор

Вид материала

Диплом

Содержание 2.2. Поиск эффективных пропорций обмена акций Игровой подход Hi = MCAPi (T+s) - MCAPi(T), i = 1, ..., n, (2.2) Условие целесообразности слияния Минимальный выигрыш Равномерное распределение эффективности Распределение дополнительного выигрыша

Подобный материал:

• Программа всероссийской научно-практической конференции «проблемы современной экономики:, 56.36kb.
• Программа и учебно-тематический план, 3846.9kb.
• Программа и учебно-тематические планы дополнительного профессионального образования, 3331.61kb.
• -, 666.3kb.
• Региональное Отделение Российского Философского Общества Саратовский государственный, 223.62kb.
• Ю. М. Трофимова (отв ред.), К. Б. Свойкин (отв секретарь), Ю. К. Воробьев, А. Н. Злобин,, 4248.82kb.
• Ю. М. Трофимова (отв ред.), К. Б. Свойкин (отв секретарь), Ю. К. Воробьев, А. Н. Злобин,, 4361.13kb.
• Автор программы: к и. н., профессор Вологдин А. А. Рецензент программы: д ю. н., профессор, 982.83kb.
• А. А. Алек- сеев, И. А. Архипова, В. Н. Бабий и др.; Под ред, 4165.68kb.
• А. С. Собенников; члены комиссии: зам председателя учебно-методической комиссии факультета, 1839.89kb.

2.2. Поиск эффективных пропорций обмена акций

Аналитические исследования слияний показывают интересные результаты: оказывается выгоднее продавать компанию, чем приобретать чужую. В большинстве случаев акционеры компаний, которые выступали продавцами в сделках по слиянию/поглощению, получили весьма существенные выгоды, а акционеры поглощающей компании выигрывали гораздо меньше [13]. Это, на мой взгляд, можно объяснить двумя причинами.

Во-первых, поглощающие компании, как правило, намного крупнее, чем поглощаемые. В этом случае при равномерном распределении чистых выгод от слияния между компаниями акционеры каждой компании получат одинаковые прибыли в абсолютном исчислении, но в относительном выражении прибыли акционеров поглощаемой компании окажутся гораздо выше.

Во-вторых, существенно содействует этому процессу конкуренция между покупателями. Каждый следующий претендент на покупку компании стремится превзойти условия, выдвинутые предыдущим. При этом все большая часть выигрыша от предстоящей сделки слияния переходит к акционерам поглощаемой компании. В то же время менеджеры компании, которую собираются поглотить, могут предпринять ряд мер противозахватного характера, добиваясь, чтобы продажа их компании, если она и наступит, произошла по самой высокой из возможных в данных условиях цене.

Однако эти моменты в сделках слияний и поглощений можно обойти, если применить разработки экономической науки, а именно рассчитать экономическую эффективность сделки, выбрать наиболее приемлемую форму интеграции и метод ее оплаты, а также построить оптимальное распределение выигрышей, что снизит риск отказа акционеров той или иной компании от совершения слияния.

Существует множество форм и методов проведения сделок по слияниям и поглощениям. Часто используются прямые переговоры между руководством и советом директоров компаний. По завершении переговоров планы представляют на утверждение акционерам обеих компаний, предметом переговоров бывают вопросы о том, что именно подлежит обмену, по какой цене, и как будет осуществлять платеж.

Обычно важнейшим результатом переговоров является соглашение об обмене акциями (stock-swap merger). В таких случаях определение цены компании-цели на самом деле оказывается установлением коэффициента обмена (конвертации) акций. Ларсон и Годенес в 1969 г. представили модель определения подобных коэффициентов [20]. Их анализ включает предположения о доходах (прибылях) и коэффициенте «кратное прибыли» (Р/Е)⁴ до и после слияния. Пусть, например, данные о чистом доходе, числе акций, прибыли на акцию (EPS), курсе акции (P_S) и отношении Р/Е будут такими, как в табл. 2. Обозначим через ER (exchage rate) коэффициент обмена, который определяется как частное от деления числа обмениваемых акций компании-покупателя (В) на число обмениваемых акций компании-цели (А). Тогда прибыль на акцию после слияния будет равна:

,

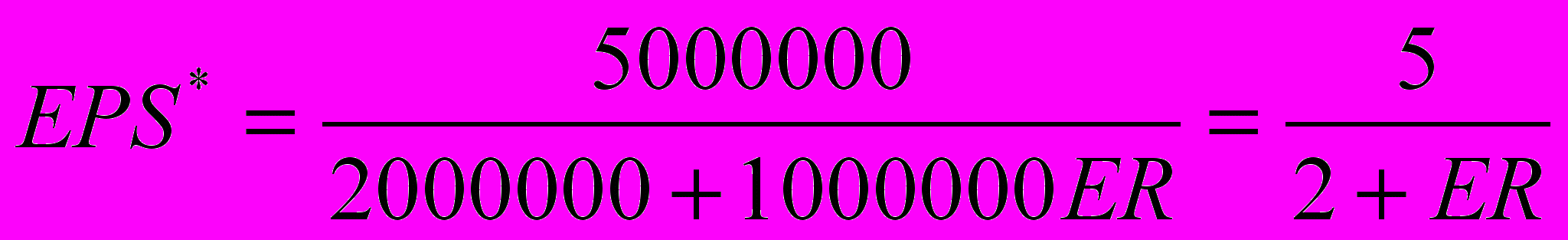а курс акции после слияния составит: 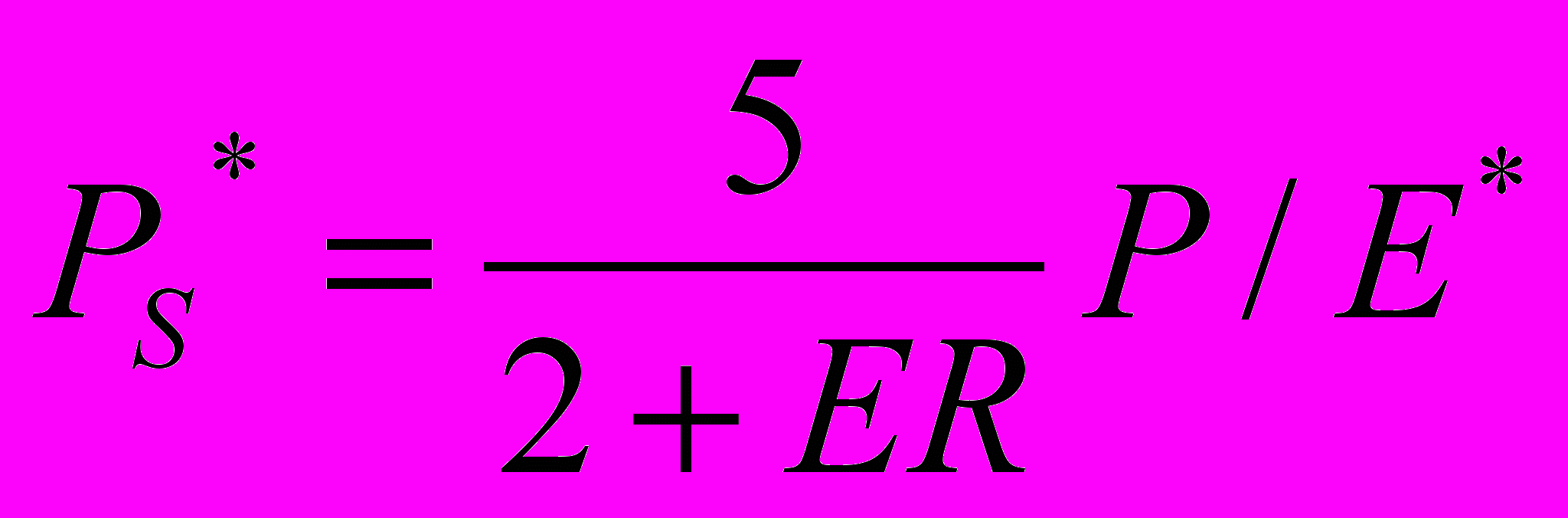, где Р/Е^* - коэффициент «кратное прибыли» (Price/Earnings ratio) после слияния.

Таблица 2

Данные по компаниям до слияния

Компания	Чистый доход (в долл.)	Число акций	EPS (в долл.)	PPS (в долл.)	P/E
А В	1 000 000 4 000 000	1 000 000 2 000 000	1 2	10 40	10 20

Чтобы положение акционеров компании В после слияния не ухудшилось, необходимо, чтобы P_S^*> P_B, то есть: 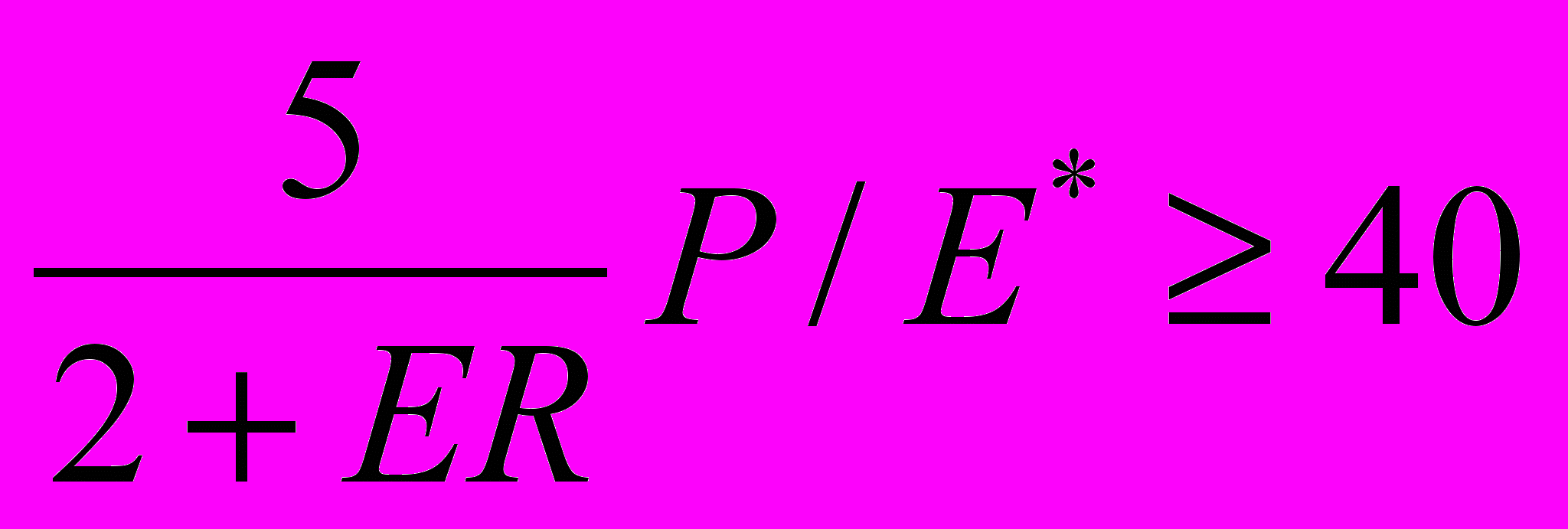. А для этого нужно, чтобы: .

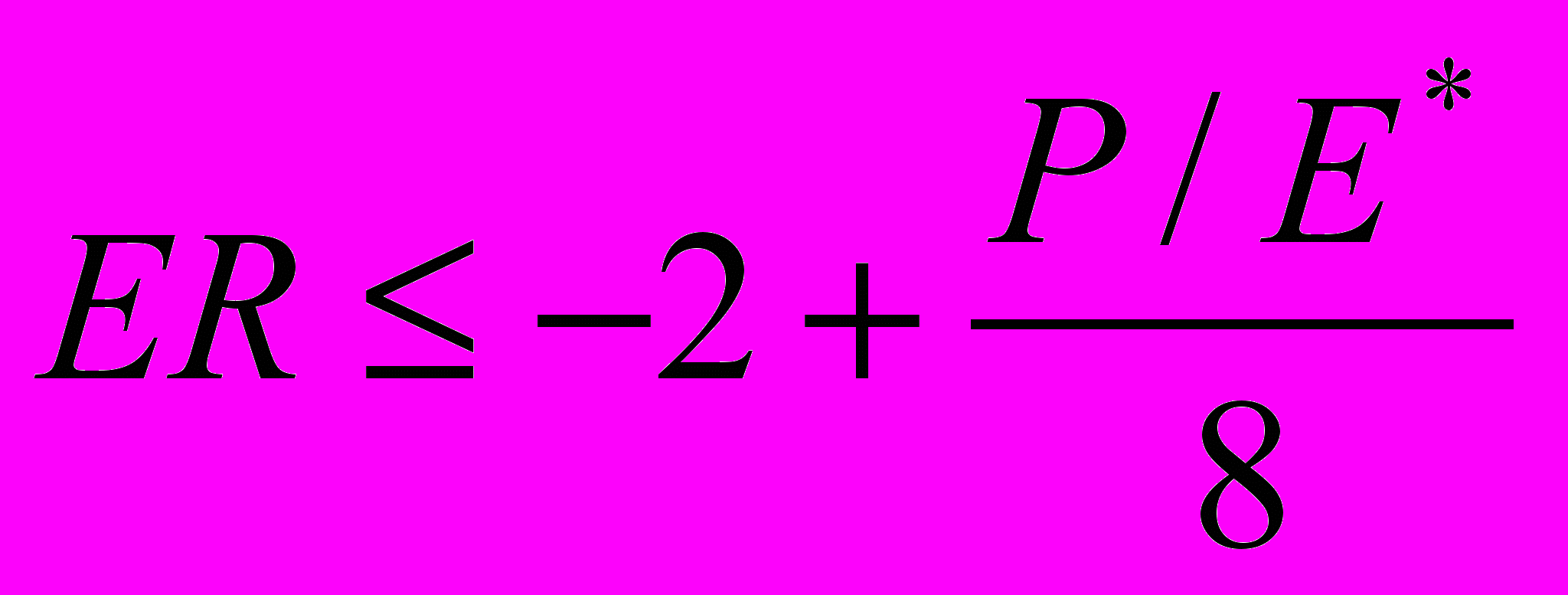А для того, чтобы после слияния положение акционеров компании А не ухудшилось, нужно, чтобы P_S^*> P_А/ER, или: 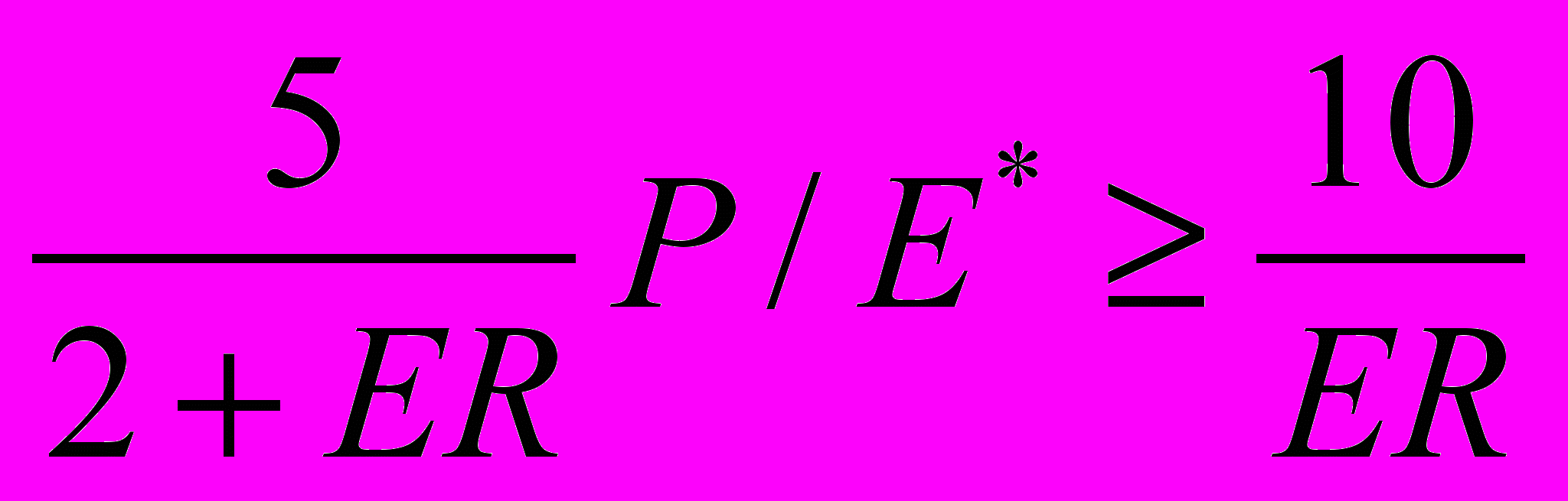, для чего требуется, чтобы: .

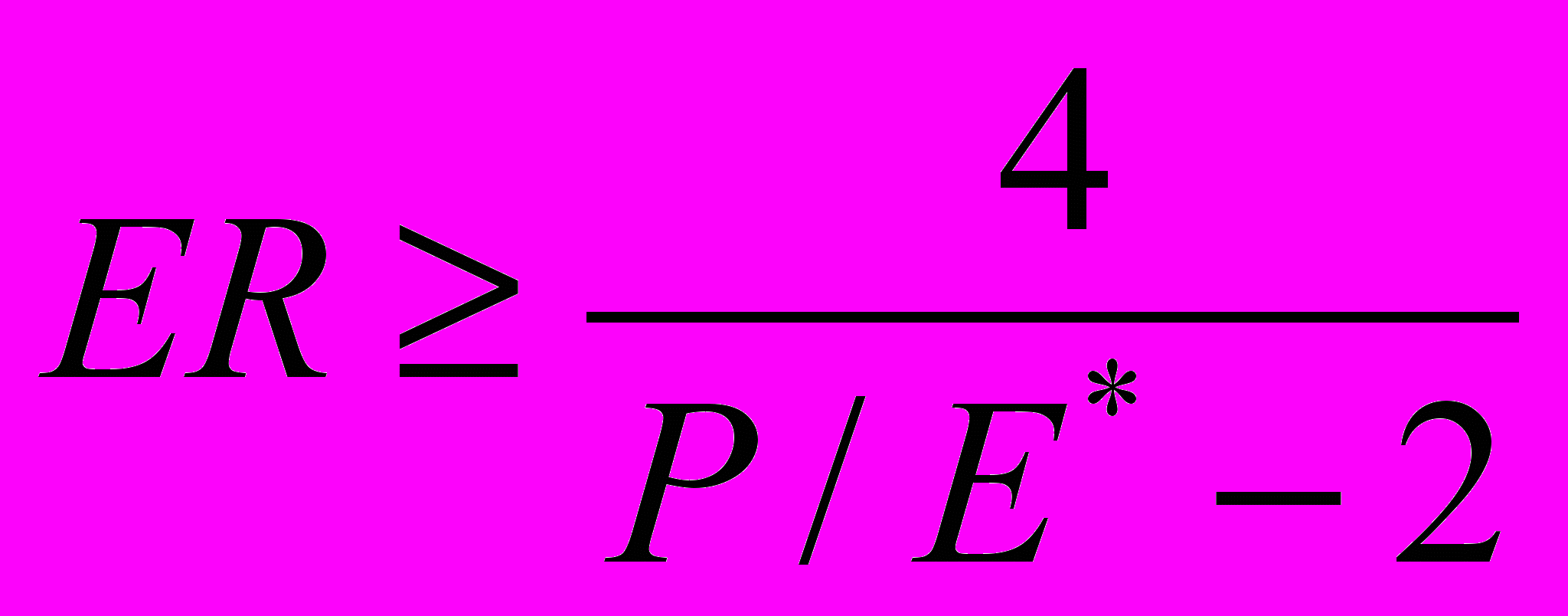Таким образом, приемлемый коэффициент обмена лежит в некотором промежутке и зависит от ожидаемого после слияния значения Р/Е^*. На рис. 4 зона переговоров обозначена Ǐ.



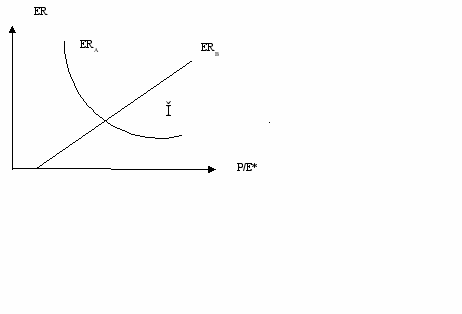
Рис. 4

Однако эта модель определяет лишь некоторую зону переговоров для коэффициента обмена, и его значение будет во многом зависеть от силы договаривающихся сторон.

В данной работе предлагается методика, основанная на теории игр, которая позволяет более точно определить эффективные коэффициенты обмена акций при слиянии компаний.

Игровой подход

Для определения коэффициентов обмена используем игровой подход, максимально учитывающий множество интересов участвующих групп лиц. Будем считать, что акционеры - владельцы обыкновенных и привилегированных акций каждой компании - являются независимыми друг от друга участниками игры.

Рассмотрим конечное множество компаний А₁, А₂, ..., А_n (множество N), имеющих для упрощения анализа одинаковую организационно-правовую форму, например открытое акционерное общество (ОАО). Единство организационно-правовой формы позволяет оперировать понятием «акционерный капитал».

Пусть k^ord = (k^ord1, ..., k^ordi, ..., k^ordn) и k^pr = (k^pr1, ..., k^pri, ..., k^prn) - коэффициенты обмена соответственно обыкновенных (ordinary) и привилегированных (preferred) акций компаний А₁, А₂, ..., А_n на акции новой компании А = А₁ + А₂ + ... + А_n. В результате завершения процесса обмена компании А₁, А₂, ..., А_n будут ликвидированы как юридические лица, а компания А станет их полным правопреемником. Данный процесс называется слиянием компаний путем образования новой.

Случай присоединения компаний А₂, ..., А_n к компании А₁ есть частный случай процесса слияния компаний при коэффициентах k^pr1 и k^ord1 равных 1. Поэтому далее будем оперировать только понятием «слияние».

Заметим, что результаты для владельцев привилегированных акций (обозначаются знаком «‘») приведем без вывода, так как они аналогичны результатам по обыкновенным акциям.

Согласно процедуре слияния компания А выпускает N^ordA обыкновенных акций, которые она обменивает на обыкновенные акции компаний А₁, А₂, ..., А_n из расчета k^ordi своих акций на одну обыкновенную акцию компании А_i:

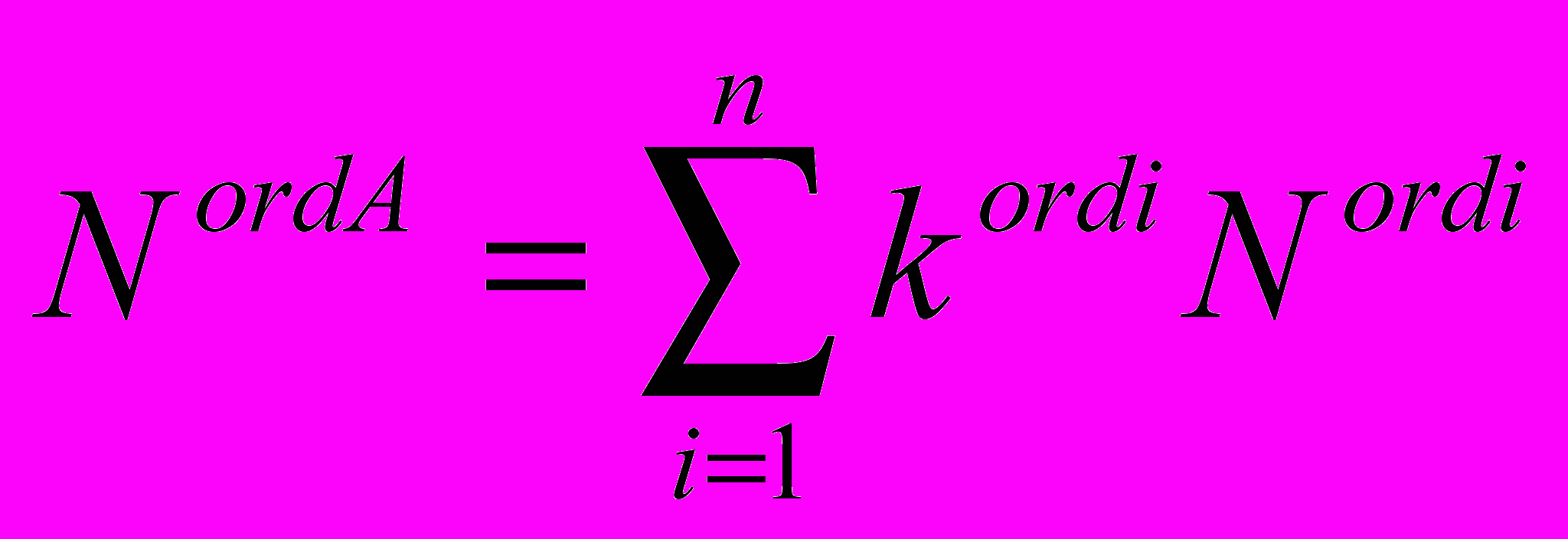(2.1)

Процедура слияния согласно корпоративному праву РФ предполагает следующую последовательность принятия решений органами управления каждой компании А_i:

• Утверждение советами директоров каждой компании коэффициентов обмена обыкновенных k^ordi и привилегированных k^pri акций.
  
• Утверждение советами директоров каждой компании цен выкупа P^pri привилегированных и P^ordi обыкновенных акций.
  
• Утверждение квалифицированным (не менее 75%) большинством присутствующих на общем или внеочередном собрании акционеров коэффициентов обмена обыкновенных k^ordi и привилегированных k^pri акций, а также цен выкупа каждого типа акций. При этом право голоса предоставляется не только владельцам обыкновенных, но и привилегированных акций [4].
  

Важно заметить, что после утверждения советами директоров коэффициентов обмена и цен выкупа должно пройти не менее 30 дней, которые по закону предоставляются акционерам для принятия решения по голосованию.

Предположим, что все акционеры действуют в условиях полной информированности, т. е. располагают полной информацией о следующих моментах:

• существующем и ретроспективном финансовом состоянии каждой компании;
  
• прогнозном финансовом состоянии каждой компании в случае их самостоятельного развития;
  
• рисках, присущих бизнесу каждой компании; прогнозах развития новой объединенной компании; риске, который будет присущ бизнесу новой компании;
  
• котировках обыкновенных и привилегированных акций каждой компании;
  
• мере ликвидности обыкновенных и привилегированных акций каждой компании.
  

Кроме того, владельцы обыкновенных и привилегированных акций - рациональные инвесторы - руководствуются исключительно критериями выгоды (гипотеза рациональности).

Суть игры в том, что владельцы обыкновенных и привилегированных акций компании А_i решают, голосовать или нет за обмен акций из расчета 1 акция за k^ordi и k^pri обыкновенных и привилегированных акций компании А.

Функция выигрыша H_i акционеров компании А_i - это разность между капитализацией, приходящейся на акционеров - владельцев обыкновенных акций компании А_i, в момент времени T+s и капитализацией компании А_i в момент времени T. Отсюда:

H^ord_i = MCAP^ord_i (T+s) - MCAP^ord_i(T), i = 1, ..., n, (2.2),

где MCAP^ord_i(T+s)- капитализация, приходящаяся на акционеров-владельцев соответственно обыкновенных акций компании А_i в момент T+s.

Предположим, что процесс объединения компаний А₁, А₂, ..., А_n успешно завершится в течение s лет после его начала в момент времени T. Тогда капитализация акций компании А_i в момент времени T+s есть определенная доля a^ordi в капитализации акций новой компании.

С учетом того, что функция капитализации является простым произведением числа акций в обращении на рыночную стоимость одной акции [16], получим выражение для определения доли a^ordi:

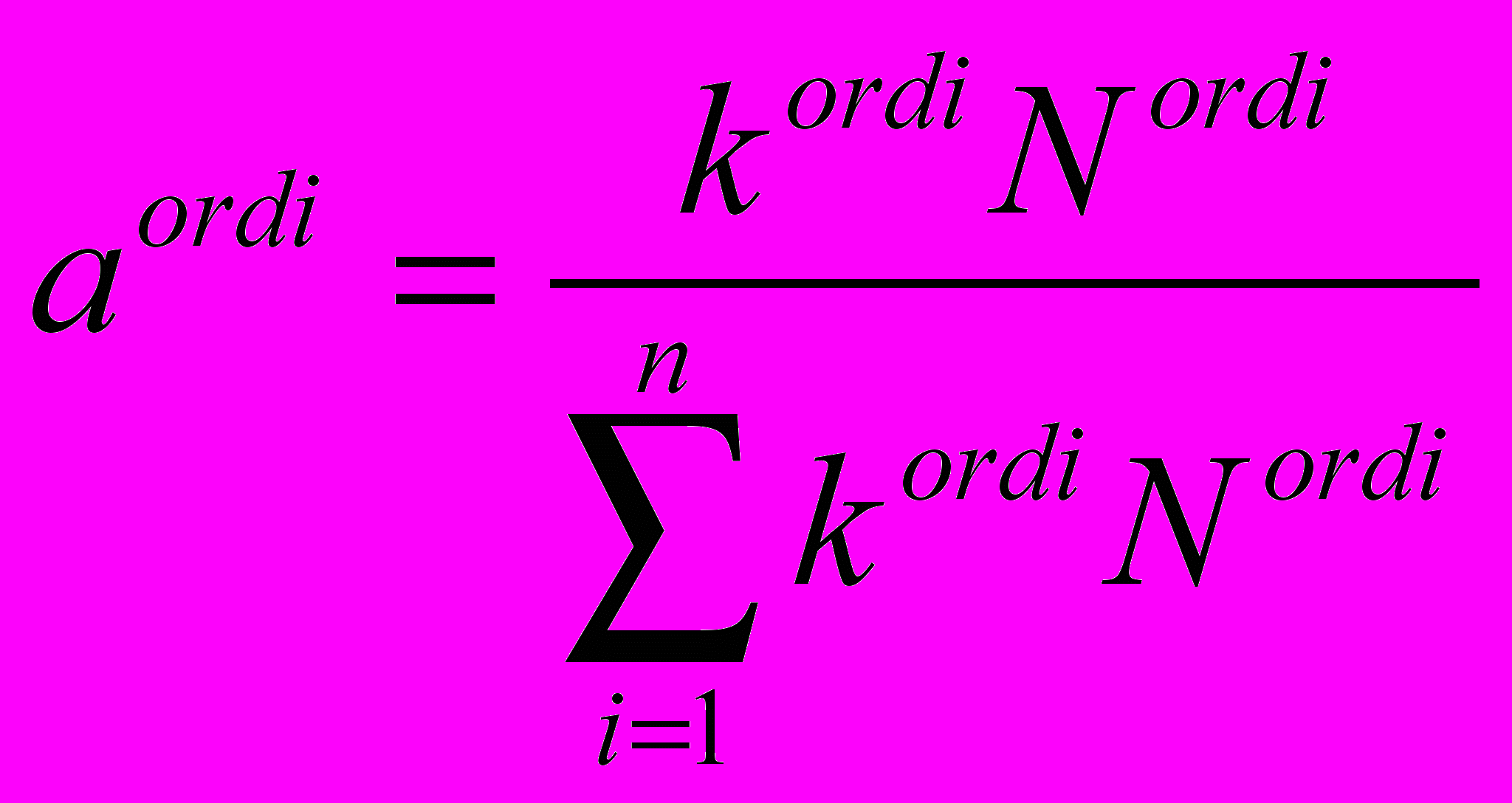, i = 1, ..., n. (2.3)

Отсюда получим новые значения функции выигрыша H_i акционеров - владельцев обыкновенных акций каждой компании А_i:

H^ord_i = a^ordiMCAP^ord_A(T+s) - MCAP^ord_i(T), i = 1, ..., n, (2.4),

где MCAP^ord_A(T+s) - капитализация обыкновенных акций новой компании А в момент завершения процесса слияния в течение s лет после его начала в момент времени T.

Из выражений (2.3) и (2.4) следует одно очевидное, но важное свойство: доли a^ordi и выигрыши H^ord_i зависят не только от коэффициентов обмена обыкновенных k^ordi акций, но и от оставшихся (n-1) коэффициентов. Следовательно, и совет директоров, и собрание акционеров компании А_i, утверждая свои коэффициенты обмена k^ordi, должны принимать во внимание коэффициенты обмена других компаний. Таким образом, органы управления компаний А₁, А₂, ..., А_n утверждая коэффициенты обмена своих акций, определяют величину выигрыша каждой компании, т. е. строят распределение общего выйгрыша. Суммарный выигрыш акционеров-владельцев обыкновенных акций равен:

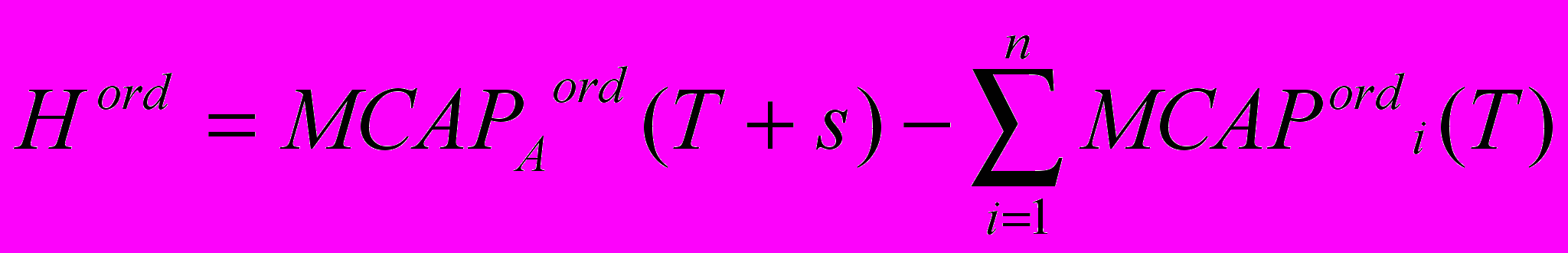(2.5),

и он не зависит от выбора коэффициентов обмена, а является в данной игре константой. Акционеры одной компании могут увеличить свой выигрыш только за счет акционеров остальных (n-1) компаний. Желание любого акционера получить максимальный эффект от слияния приводит к конфликту интересов.

Задача данной модели состоит в нахождении оптимального распределения суммарного выигрыша через определение эффективных коэффициентов обмена.

УСЛОВИЕ ЦЕЛЕСООБРАЗНОСТИ СЛИЯНИЯ

Допустим, акционеры каждой компании располагают возможностью определить стратегию развития фирмы из множества альтернатив. Оценивая каждый вариант развития бизнеса, владельцы акций на любом временном интервале могут рассчитать NPV^ord_i денежного потока, приходящегося на принадлежащие им акции компании А_i.

При анализе эффективности вложений в акции той или иной компании NPV^ord_i денежного потока акционера компании А_i есть разность между приведенной стоимостью акций компании в момент T+s и приведенной стоимостью ожидаемых за s лет дивидендов и стоимостью акций компании в момент T:

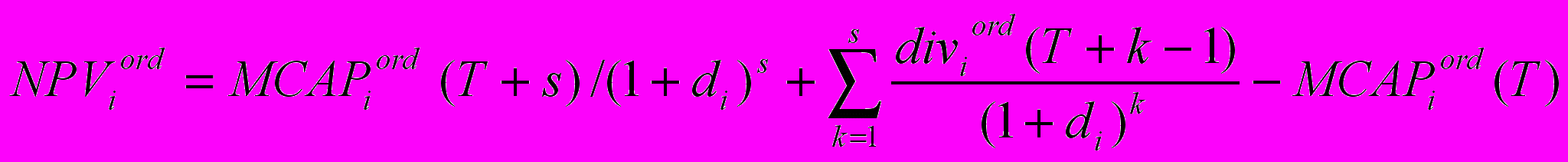,i=1, ..., n, (2.6)

где div^ord_i(T+k-1) - дивиденд за (k-1)-й год по обыкновенным акциям компании А_i после слияния при k=1, ..., s; d_i - ставка дисконта, отражающая риски вложения в акцию компании А_i.

В случае если акционеры-владельцы обыкновенных акций голосуют за слияние, функционал (2.6) можно записать в следующем виде:

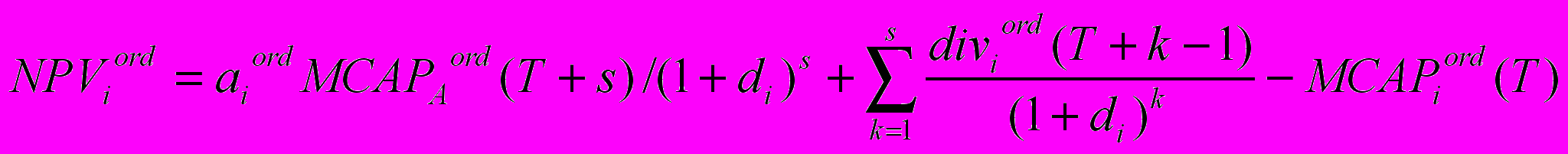, i=1, ..., n. (2.7)

Для того чтобы голосование «за» по вопросу слияния отвечало гипотезе рациональности, необходимо, чтобы значение функционала (2.7) было не меньше, а с учетом расходов на слияние строго больше значения функционала (2.6). Тогда получаем:

a^ord_iMCAP^ord_A(T + s) > MCAP^ord_i(T + s), i = 1, ..., n. (2.8)

Следовательно, при соблюдении условий (2.8) и аналогичных (2.8’) акционеры каждой компании А_i - не будут иметь объективных предпосылок голосовать против слияния.

Предположим, что на предварительном этапе все акционеры проголосовали за слияние, положительно ответив на вопрос о целесообразности.

Несмотря на очевидный факт возможности ущемить права акционеров-владельцев привилегированных акций и права миноритарных акционеров-владельцев обыкновенных акций, не имеющих представителей в советах директоров компаний, опыт проведения слияний в мире и России доказывает, что с данными классами акционеров всегда проводятся конструктивные консультации [26]. Риски, присущие процессам слияния, существенны, и затраты, связанные с сопровождением данного процесса, значительны. Как следствие, перед инициатором слияния стоит не только задача полного устранения рисков, но и управления ими на всех этапах проведения слияния.

Отсюда следует, что инициатор слияния будет стремиться минимизировать риски по слиянию. Самым эффективным способом управления данным риском является учет интересов всех участвующих сторон и оптимальное распределение эффекта от слияния для всех акционеров - владельцев как обыкновенных, так и привилегированных акций.

Таким образом, мы в общем случае определили условия целесообразности, выполнение которых создает предпосылки голосования за слияние. Однако соответствие этим условиям не является достаточным для акционеров каждой компании при выборе варианта «за» или «против». В существенной степени именно критерии оптимальности могут обеспечить объективные условия для положительного итога голосования на собрании акционеров каждой компании.

Вопрос голосования за или против слияния принадлежащими каждому акционеру голосами приводит нас к задаче принятия решения в условиях столкновения интересов различных сторон. Располагая полной информацией, акционеры-владельцы обыкновенных акций будут принимать такое решение о коэффициентах обмена своих акций k^ordi, чтобы получить максимальный выигрыш H^ord_i. Однако функция выигрыша H^ord_i зависит не только от решения совета директоров компании А_i, но и от решений советов директоров других компаний. Поэтому коэффициент k^ordi, дающий большее значение выигрыша для акционеров компании А_i, может не быть таковым для акционеров других компаний.


МИНИМАЛЬНЫЙ ВЫИГРЫШ

С момента принятия советом директоров каждой компании решения о коэффициентах обмена k^ordi каждому акционеру известно множество коэффициентов обмена k^ord = (k^ord1, ..., k^ordi, ..., k^ordn) акций. Следовательно, в течение не менее 30 дней акционеры имеют возможность взвесить и рассчитать не только эффективность проведения обмена по предложенным коэффициентам, но и ответить на вопрос о целесообразности, используя условие (2.8). Минимальное требование, предъявляемое к коэффициентам обмена k^ord = (k^ord1, ..., k^ordi, ..., k^ordn), должно обращать (2.8) в равенство.

В результате некоторых преобразований получим выражение для коэффициентов обмена обыкновенных акций:

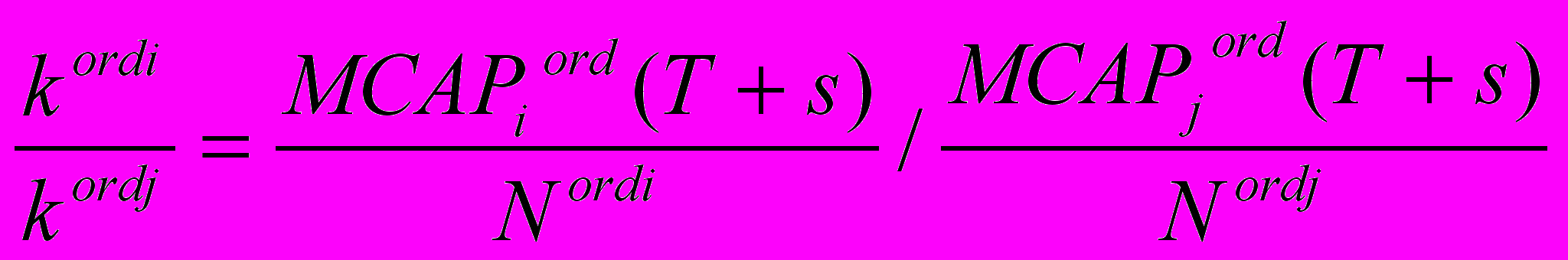, i = 1, ..., n, j = 1, ..., n (2.9).

Назовем коэффициенты обмена обыкновенных акций k^ord = (k^ord1, ..., k^ordi, ..., k^ordn), удовлетворяющие (2.9), минимально целесообразными, а распределяемый выигрыш, суммарно равный:

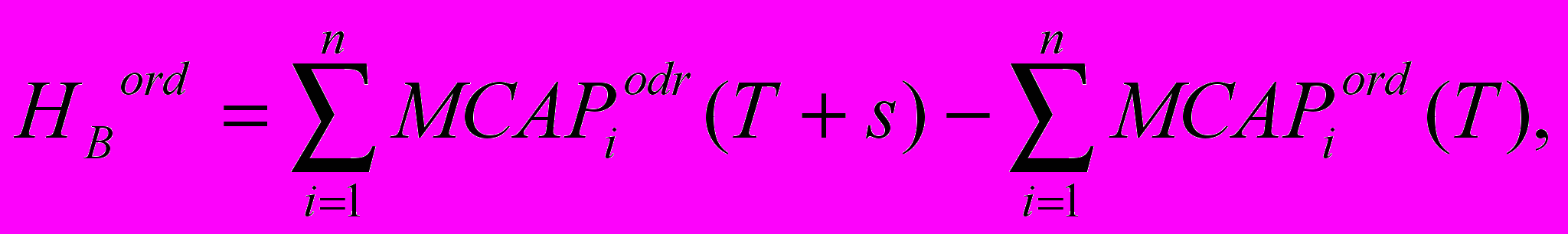i = 1, ..., n, (2.10)

основным выигрышем.

Таким образом, если знать прогноз развития каждой компании и полагать, что капитализация обыкновенных акций новой компании равна сумме прогнозных значений капитализации обыкновенных акций всех объединяющихся компаний, то можно рассчитать коэффициенты обмена, соответствующие минимальному выигрышу.

Предсказать функцию капитализации обыкновенных акций всех объединяющихся компаний на s лет вперед нелегко, однако это возможно на основе оценки стоимости 100% обыкновенных акций компании, например, с помощью DCF-метода, позволяющего оценить будущую стоимость 100% обыкновенных акций компании и применить результаты к расчету коэффициентов обмена по методу минимального выигрыша.

Основной недостаток данного метода в том, что если капитализация обыкновенных акций новой компании А превысит сумму прогнозных значений капитализации обыкновенных акций всех объединяющихся компаний, то в результате слияния появятся компании, акционеры которых получат выигрыш выше минимального.

Если первые (n-1) компании определили минимально целесообразные коэффициенты обмена, то последняя компания получает не только минимальный выигрыш, но и дополнительный, нераспределенный между первыми (n-1) компаниями. Тогда эффективность операции конвертации - выигрыш в результате слияния (2.4) будет у последней компании выше, чем у остальных. Более того, применение принципа оптимальности - минимального выигрыша - не гарантирует равенства получаемой от слияния эффективности. С учетом погрешностей прогнозных оценок, которые служат основой для расчета минимально целесообразных коэффициентов обмена, отношение дохода от конвертации к капитализации в момент T будет у одних компаний выше, чем у других.

Следовательно, существует риск того, что относительно «проигравшие» компании могут отклонить или отсрочить процесс слияния. Попыткой решения данной проблемы является поиск коэффициентов обмена, задающих равномерное распределение эффективности.

РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ ЭФФЕКТИВНОСТИ

Определим такие коэффициенты обмена обыкновенных акций компаний А₁, А₂, ..., А_n, чтобы операция конвертации была одинаково эффективна для акционеров каждой компании:

H^ord₁/MCAP^ord₁(T) = ... = H^ord_i/MCAP^ord_i(T) = ... = H^ord_n/MCAP^ord_n(T) (2.11).

Назовем принцип равенства получаемой каждым акционером эффективности вложений на свои акции равномерным распределением эффективности.

С учетом (2.3) и (2.4) получим из (2.11) коэффициенты обмена обыкновенных акций:=….

Отсюда получаем критерий оптимальности:

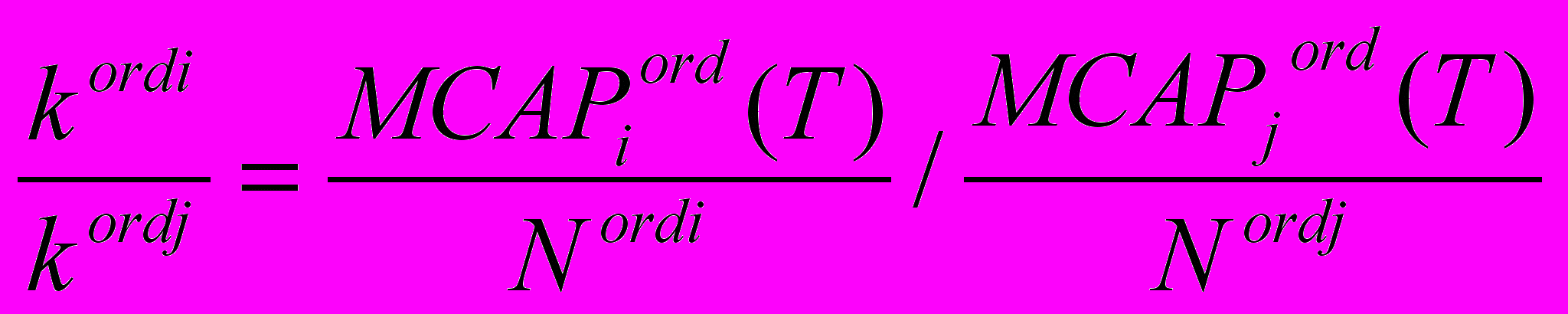i = 1, ..., n, j = 1, ..., n (2.12).

Назовем коэффициенты k^ord = (k^ord1, ..., k^ordi, ..., k^ordn), удовлетворяющие (2.12), равномерно равновесными. Аналогичное решение (2.12’) верно и для коэффициентов обмена привилегированных акций. Из (2.12) также следует, что: .

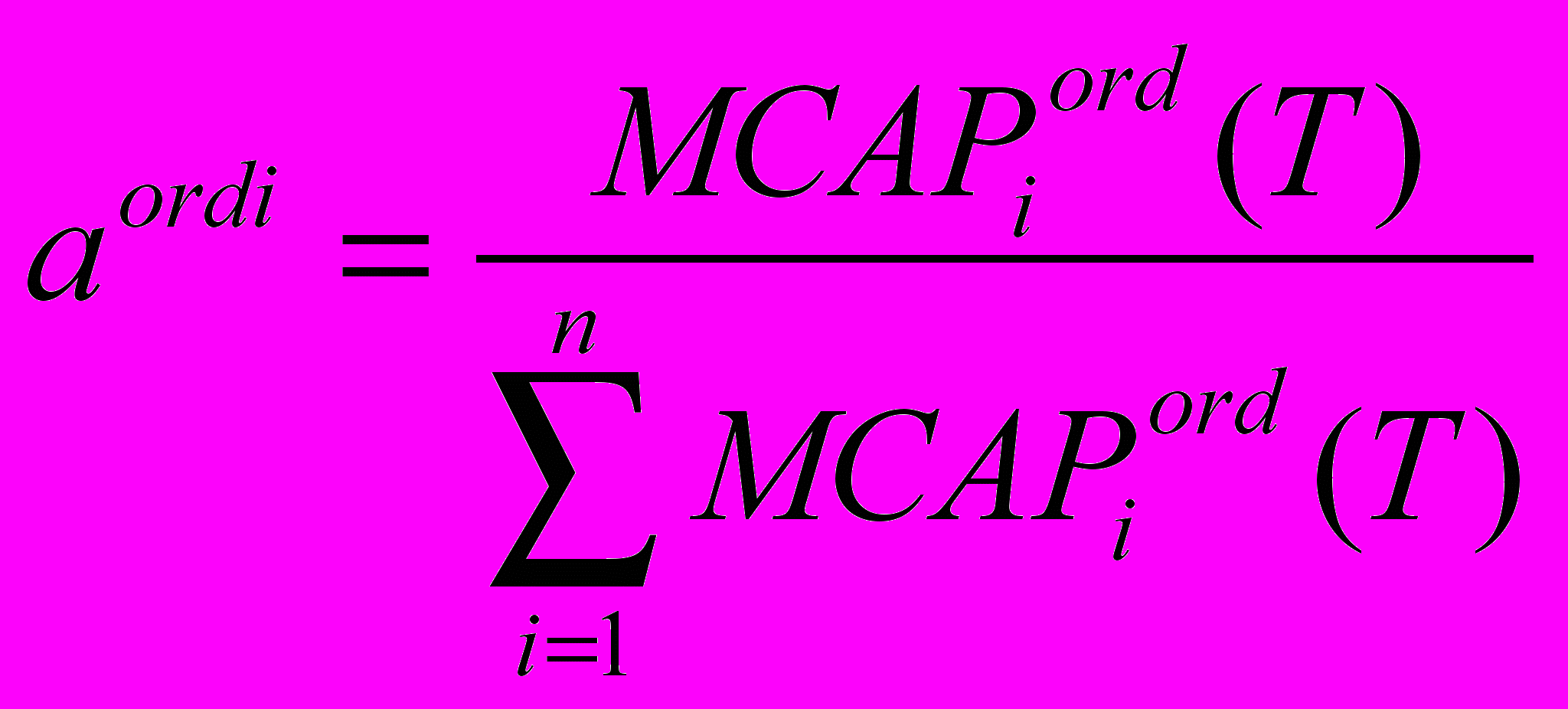Выражения (2.12) и (2.12’) определяют коэффициенты обмена, которые должны быть предложены к утверждению советом директоров каждой компании А_i. Если коэффициенты обмена будут отличаться от равномерно равновесных, то найдется компания, акционеры которой сопоставят эффективность обмена своих акций и акций прочих обществ и решат, что их права ущемлены. Возникнет реальный риск, что при значительном расхождении эффективности обмена одной компании от прочих акционеры данной компании на собрании акционеров проголосуют против предложенных пропорций обмена.

Таким образом, равномерно равновесные коэффициенты обмена являются оптимальными, удовлетворяющими интересам акционеров всех компаний.

Заметим, что формула (2.12) является частным случаем формулы (2.9) при s = 0. То есть при предположении, что не существует временных затрат на присоединение, существует единственное решение, определяемое (2.12), удовлетворяющее критериям оптимальности.

Рассмотрим вопрос целесообразности с учетом полученного критерия оптимальности. При помощи некоторых преобразований получим уточнение условий целесообразности для акционеров из (2.8) с учетом (2.12):

MCAP^ord_A(T + s)/ 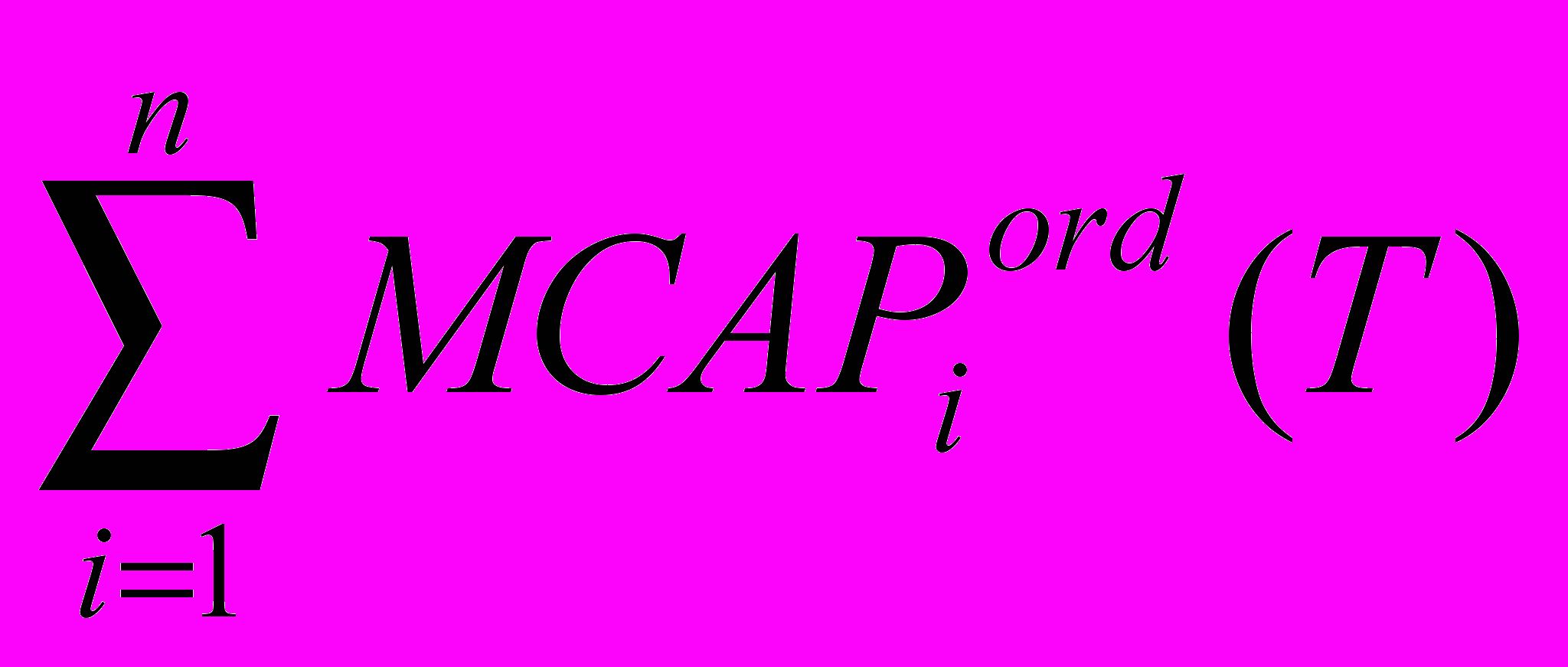> MCAP^ord_i(T + s)/MCAP^ord_i(T), i = 1, ..., n (2.13).

Таким образом, в случае определения равномерно равновесных коэффициентов обмена отношение капитализации новой компании А в момент T+s к сумме показателей текущей капитализации всех компаний должно быть больше отношения капитализации каждой компании А_i, достигаемой при любом сценарии самостоятельного развития к моменту T+s, к текущей капитализации компании А_i. Заметим, что условие (2.8) позволяло ответить на вопрос целесообразности через увеличение доли компании А_i в новой компании за счет соответствующего уменьшения суммарной доли остальных компаний.

При равномерно равновесных коэффициентах обмена вопрос целесообразности полностью определяется показателем капитализации новой компании А.

Уточненные критерии целесообразности (2.13) и наличие одной степени свободы систем уравнений (2.12) позволяют нам использовать критерий максимизации. Выберем такой номер i^ord, при котором достигается максимум величины, стоящей в правой части неравенства (2.13). Тогда достаточно подобрать такой k^ordi, чтобы выполнялось (2.8). Таким образом, мы получим коэффициенты обмена обыкновенных акций k^ord = (k^ord1, ..., k^ordi, ..., k^ordn), которые одновременно являются оптимальными и соответствующими критериям целесообразности.

Однако равномерное распределение эффективности не гарантирует достаточности величины распределяемого выигрыша. Этот вопрос также определяется капитализацией обыкновенных акций новой компании.

Определение оптимальных пропорций обмена возможно в некоторых частных случаях единственным образом. В общем случае решения, удовлетворяющего всем перечисленным критериям, может не существовать.


РАСПРЕДЕЛЕНИЕ ДОПОЛНИТЕЛЬНОГО ВЫИГРЫША

Нашу модель можно расширить до игры с положительным дополнительным выигрышем, которая рассчитывает искомые коэффициенты обмена. Согласно этой игре, суммарный выигрыш акционеров-владельцев обыкновенных акций равен:

H^ord = H^ord_B+ H^ord_add, (2.14),

где основной выигрыш H^ord_B определяется (2.10), а дополнительный выигрыш равен:

H^ord_add = MCAP^ord_A(T + s) - 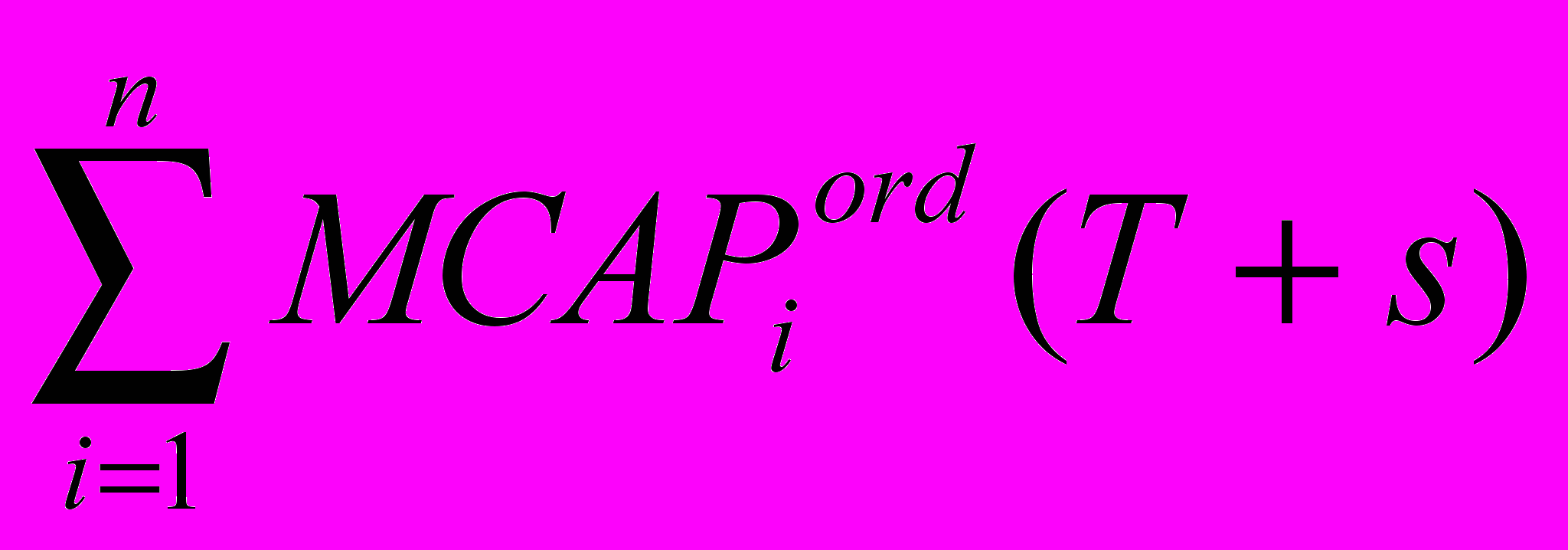(2.15).

Поиск оптимальных коэффициентов свелся, таким образом, к решению задачи распределения дополнительного выигрыша, получаемого владельцами обыкновенных и привилегированных акций. Из (2.10), (2.14) и (2.15) следует, что: .

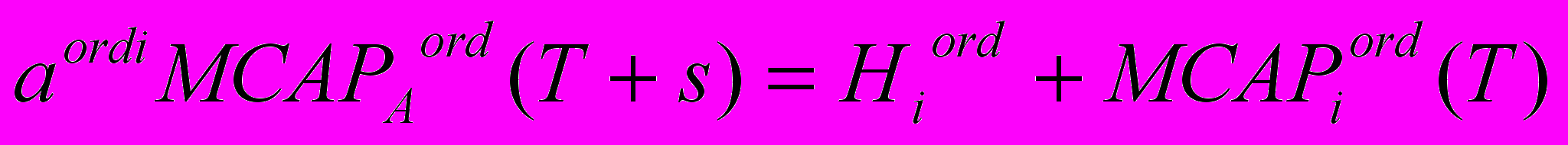Коэффициенты обмена обыкновенных акций будут соответствовать следующему равенству:

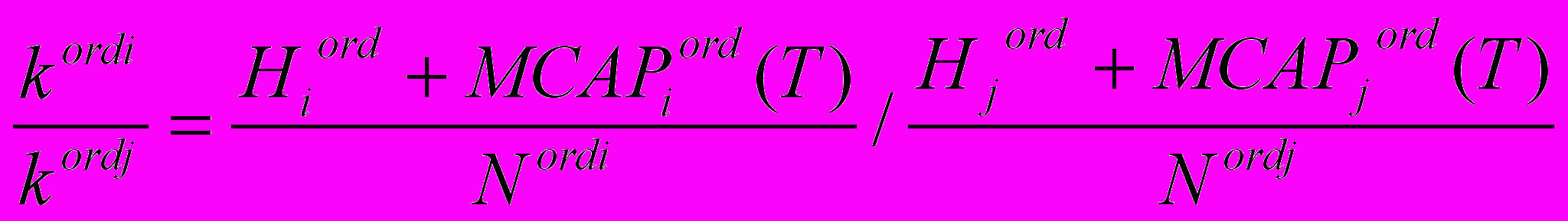, i = 1, ..., n, j = 1, ..., n (2.16).

Коэффициенты обмена, найденные по (2.16), удовлетворяют критериям целесообразности, реализуемости и оптимальности. Если дополнительный выигрыш больше нуля, то существует множество решений, соответствующих этим критериям. Вариант равного распределения дополнительного выигрыша между компаниями несправедлив по отношению к более крупным компаниям, логичнее распределить его согласно пропорции капитализации каждой компании в момент времени T в общей суммарной капитализации. Такое распределение должно снизить риск голосования акционеров против сделки.