Программа квалификационного экзамена для педагогических и руководящих работников образовательных учреждений Хабаровского края, претендующих на высшую квалификационную категорию г. Хабаровск

Вид материала

Программа

Содержание Учитель математики 2. Выражения и преобразования 3. Уравнения и неравенства 5. Элементы комбинаторики, статистики и теории вероятностей. 6. Геометрические фигуры и их свойства.

Подобный материал:

• Тестирования, 593.8kb.
• На включение программы повышения квалификации педагогических и руководящих работников, 169.75kb.
• Список аттестуемых педагогических и руководящих работников на первую квалификационную, 2196.17kb.
• Ьской сош полностью, поэтому электронные варианты презентаций и слайдов к предлагаемой, 1417.09kb.
• Положение о формах и процедурах аттестации педагогических и руководящих работников, 694.74kb.
• Расписание курсов повышения квалификации, краткосрочных и проблемных курсов и семинаров, 2773.86kb.
• На включение программы повышения квалификации педагогических и руководящих работников, 370.56kb.
• На включение программы повышения квалификации педагогических и руководящих работников, 198.87kb.
• Методическое объединение учителей математики, физики, информатики Председатель мо продайко, 14.07kb.
• Саратовская городская дума решение, 419.86kb.

Учитель математики

1. 
   Числа и вычисления
   

Делимость целых чисел. Свойства делимости. Деление с остатком. Принцип Дирихле.

Комплексные числа. Геометрическая интерпретация комплексных чисел. Алгебраическая и тригонометрическая формы записи комплексных чисел. Арифметические действия над комплексными числами. Комплексно сопряженные числа. Возведение в натуральную степень (формула Муавра). Основная теорема алгебры.

Среднее арифметическое, среднее геометрическое, среднее квадратичное и среднее гармоническое неотрицательных чисел. Соотношения между ними.

Метод математической индукции.

Проценты. Задачи на сложные проценты. Пропорции.

Текстовые задачи: задачи на движение, задачи на работу; задачи на концентрацию смеси и сплавы.


2. Выражения и преобразования

Тождественные преобразования степенных, логарифмических, иррациональных, тригонометрических выражений; нахождение значений выражений.


3. Уравнения и неравенства

3.1. Тригонометрические уравнения. Отбор корней.

Логарифмические, показательные, иррациональные уравнения. Использование нескольких приемов при решении уравнений. Решение комбинированных уравнений.

Уравнения, содержащие переменную под знаком модуля. Уравнения с параметрами. Использование графиков при решении уравнений.

Решение уравнений высших степеней. Теорема Безу и её следствия. Схема Горнера.

3.2. Неравенства с одной переменной: рациональные, показательные, логарифмические, комбинированные. Использование графиков при решении неравенств.

Неравенства, содержащие переменную под знаком модуля. Неравенства с параметром. Системы и совокупности неравенств.

3.3. Уравнения и неравенства с двумя переменными, их системы. Геометрическая интерпретация решений.


4. Функции

Числовые функции и их свойства:

• область определения и множество значений функции;
  
• непрерывность функции;
  
• монотонность функции;
  
• промежутки знакопостоянства;
  
• ограниченность функции;
  
• периодичность функции;
  
• экстремумы функции, наибольшее (наименьшее) значение функции;
  

График функции. Построение графиков функций, заданных различными способами. Преобразования графиков функций: параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой 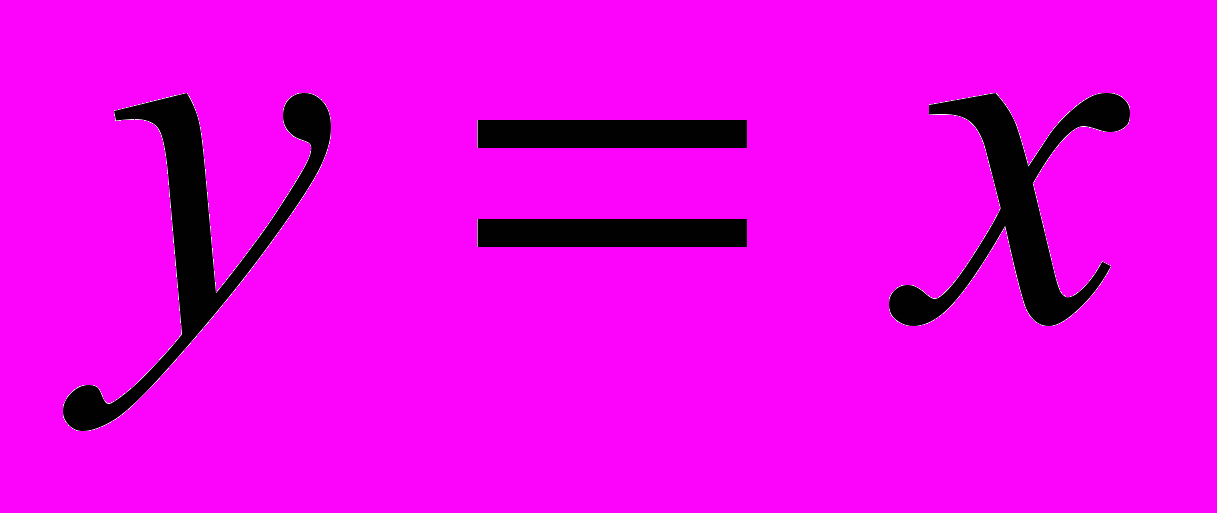, растяжение и сжатие вдоль осей координат.

Элементарные функции в школьном курсе математики. Связь между свойствами функции и ее графиком. Исследование сложной функции элементарными методами.

Сложная функция (композиция функций). Взаимно обратные функции. Область определения и область значений обратной функции. График обратной функции. Нахождение функции, обратной данной. Обратные тригонометрические функции, их свойства и графики.

Примеры функциональных зависимостей в реальных процессах и явлениях.

Предел функции в точке. Понятие о непрерывности функции. Точки разрыва. Основные теоремы о непрерывных функциях. Поведение функций на бесконечности. Асимптоты графиков функций.

Производная функции. Применение производной к исследованию функций и построению графиков. Использование производных при решении уравнений и неравенств, при решении текстовых, физических и геометрических задач, нахождении наибольших и наименьших значений.

Вторая производная и ее физический смысл. Исследование графиков функций на выпуклость и точки перегиба.

Первообразная и неопределённый интеграл. Площадь криволинейной трапеции. Определённый интеграл. Примеры применения интеграла в физике и геометрии.


5. Элементы комбинаторики, статистики и теории вероятностей.

Табличное и графическое представление данных. Числовые характеристики рядов данных.

Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений.

Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля.

Элементарные и сложные события. Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события.


6. Геометрические фигуры и их свойства.

Измерение геометрических величин.

Основные фигуры планиметрии их свойства: треугольник, параллелограмм, трапеция, правильные многоугольники, окружность. Окружность, вписанная в многоугольник. Окружность, описанная около многоугольника. Замечательные точки треугольника: точки пересечения серединных перпендикуляров, биссектрис, медиан. Окружность Эйлера. Площади.

Углы и расстояния в пространстве.

Многогранники. Вершины, ребра, грани многогранника. Теорема Эйлера. Развертка многогранника.

Тела и поверхности вращения. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения, параллельные основанию. Шар и сфера, их сечения. Эллипс, гипербола, парабола как сечения конуса. Объёмы, площади поверхностей.

Комбинации многогранников и тел вращения.

Метод координат в пространстве. Координаты вектора в пространстве: длина, угол между двумя векторами, условия коллинеарности и ортогогнальности в пространстве.

Уравнения сферы и плоскости. Формула расстояния от точки до плоскости.