Geum.ru

[Текст]: научно-аналитический журнал (издаётся с 2007 г.)

Вид материалаДокументы

Содержание


А. Г. Санников, Т. Х. Тимохина, Н. С. Соколовский ВЫЧИСЛИТЕЛЬНАЯ СИСТЕМА «ГРУППОВОЙ КОСИНОР-АНАЛИЗ»
Ключевые слова
Подобный материал:
1   ...   26   27   28   29   30   31   32   33   34

А. Г. Санников, Т. Х. Тимохина, Н. С. Соколовский

ВЫЧИСЛИТЕЛЬНАЯ СИСТЕМА «ГРУППОВОЙ КОСИНОР-АНАЛИЗ»



Аннотация: в статье рассматривается математический аппарат косинор-анализа, предназначенный для выявления параметров группы биологических ритмов. Также рассматривается программное обеспечение, реализующее данный аппарат.

Annotation: The article represents a mathematical machine for cosinor methodology designed for setting the parameters of biological rhythms. It also describes the software.

Ключевые слова: хронобиология, хрономедицина, косинор-анализ, информатизация в медицине.

Key words: chronobiology, chronomedicine, cosinor methodology, informatization in medicine.


В последние три десятилетия во всем мире отмечается повышенный интерес к изучению ритмической организации процессов в организме как в условиях нормы, так и патологии. В настоящее время у человека изучены многие физиологические процессы, ритмически меняющиеся во времени. Многие патологические процессы в организме сопровождаются нарушением временной организации физиологических функций. В то же время рассогласование ритмов является одной из причин развития патологических процессов, так называемых десинхронозов. В попытке изучить это явление возникла новая междисциплинарная фундаментальная наука – хронобиология. На сегодняшний день активно разрабатываются методы хронодиагностики, хронотерапии и хронопрофилактики. Выясняются причины общей и частной хронопатологии. Все эти достижения в области хрономедицины не только характеризуют ее как новое направление в медико-биологической науке и практике, но и создают основу для перехода медицины на более высокий качественный уровень.

Очевидно, что применение в исследовании адекватных поставленным задачам методов обязательно, поскольку этим в значительной мере определяется правильность и полнота решения задач. Предложенный для обработки данных биоритмов метод косинор-анализа получил широкое распространение и для большинства исследований является по существу единственным методом обработки биоритмических данных.

Выявление и оценка любого периодического процесса предусматривает обработку временного ряда наблюдений. При описании ритмики преследуют следующие цели: выявление ритмических составляющих и, если таковые будут обнаружены, оценка параметров ритма. Любой анализ временного ряда следует начинать с определения длины периода. Если наблюдения равноотстоящие, то можно применять Фурье-анализ и вычисление автокорреляционной функции. При неравноотстоящих наблюдениях возможны два решения. Первое состоит в том, чтобы превратить ряд с неравноотстоящими наблюдениями в равноотстоящий, например, с помощью интерполяции. Однако, подобное решение вносит дополнительную погрешность в вычисления. Второй подход основан на описании ряда синусоидами по методу наименьших квадратов. Если менять период пробной синусоиды и каждым оценивать качество аппроксимации с помощью вычисления корреляционного отношения и погрешности амплитуды, то на кривой, отражающей эту зависимость (периодограмме), образуются пики. Последние соответствуют периодам, имеющимся в процессе, в то время как высота пиков – степени приближенности синусоидальной модели. Из достоинств этого метода следует отметить то, что выявить наличие ритмичности можно даже в том случае, когда сигнал имеет отличную от синусоиды форму.

Поскольку синусоидальная аппроксимация занимает ключевое положение в построении периодограммы, приведем основные моменты расчетов.

Для начала рассчитываются такие показатели, как мезор М, представляющий собой среднее арифметическое, амплитуда А – максимальное отклонение от мезора и акрофаза Ak – наибольшее значение процесса. Далее необходимо провести аппроксимацию ряда с периодом T: 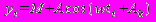. Где, yi – значение аппроксимированной ординаты (величина процесса), а ti – значение на абсциссе (время). Угловая частота рассчитывается по формуле: 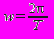. Следует отметить, что пробный период задается самостоятельно, и, как правило, не превышает минимальной разницы между отстоящими точками наблюдений.

Следующим этапом необходимо рассчитать квадратную матрицу:





и обратную ей матрицу . Формулы для вычисления обратной матрицы мы приводить не будем, так как они являются стандартными. Используя элементы обратной матрицы, необходимо вычислить коэффициенты нормального уравнения:








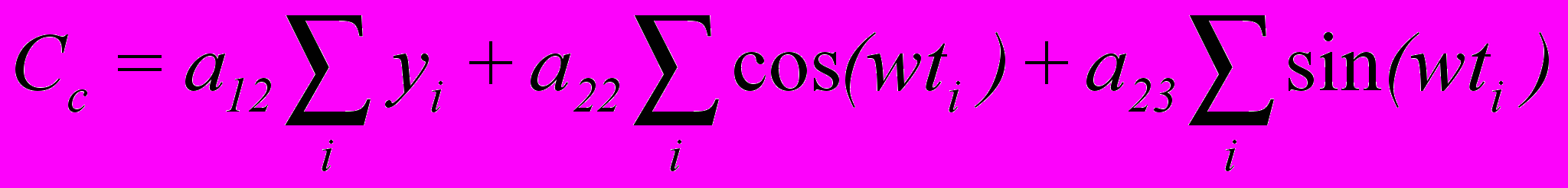
После чего находится остаточная сумма квадратов:







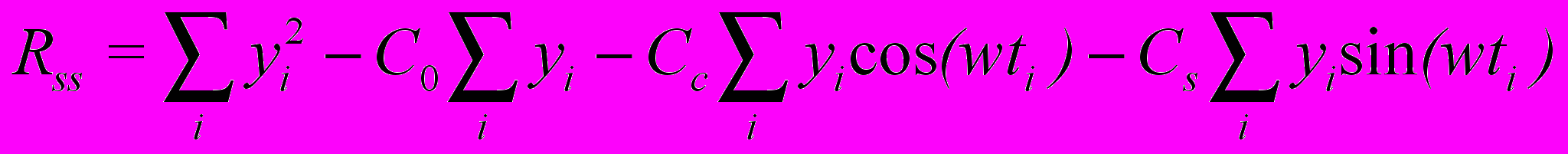
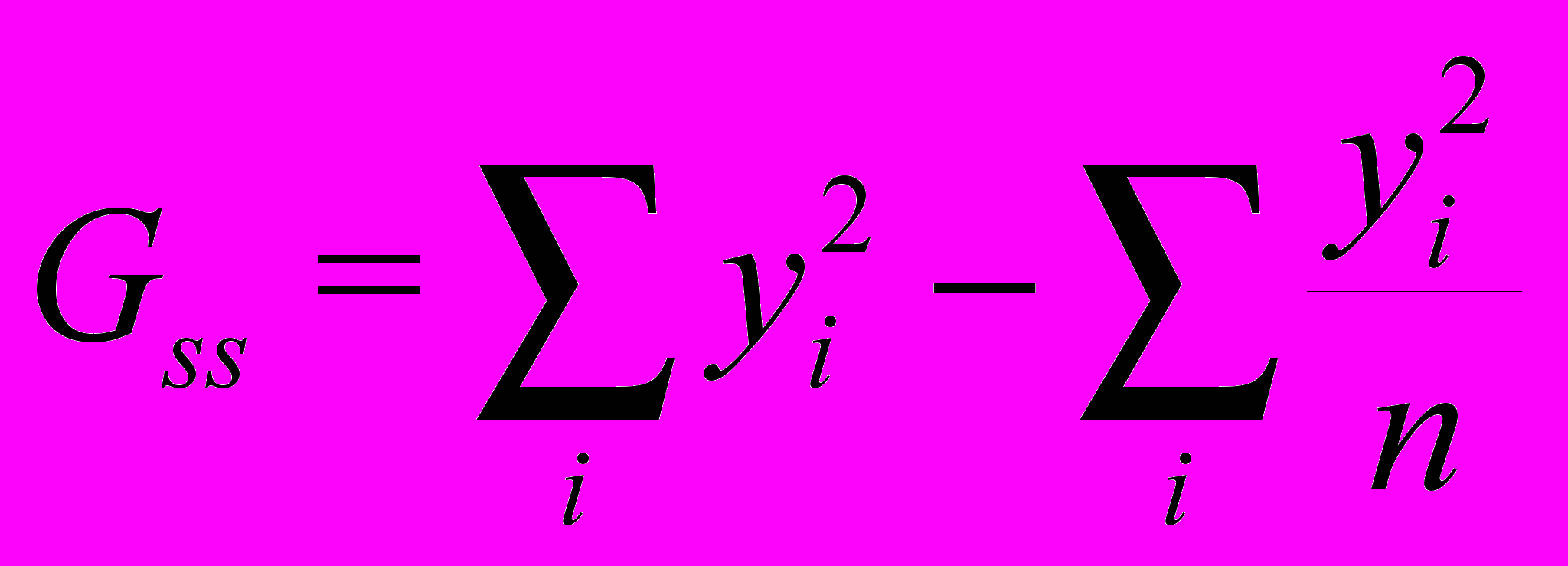
и квадрат корреляционного отношения, который необходим для оценки доли полезного сигнала:. На этом этап расчета модели с пробным периодом заканчивается. Далее необходимо увеличить период на шаг dT, который задается самостоятельно и не превышает 1/50 длины временного ряда. После чего необходимо заново рассчитать модель.

Расчеты следует повторять до тех пор, пока период не станет равным введенному временному ряду.

Дальнейшие вычисления необходимо проводить только для модели с наибольшим .

Последним этапом расчетов является нахождение погрешности амплитуды: 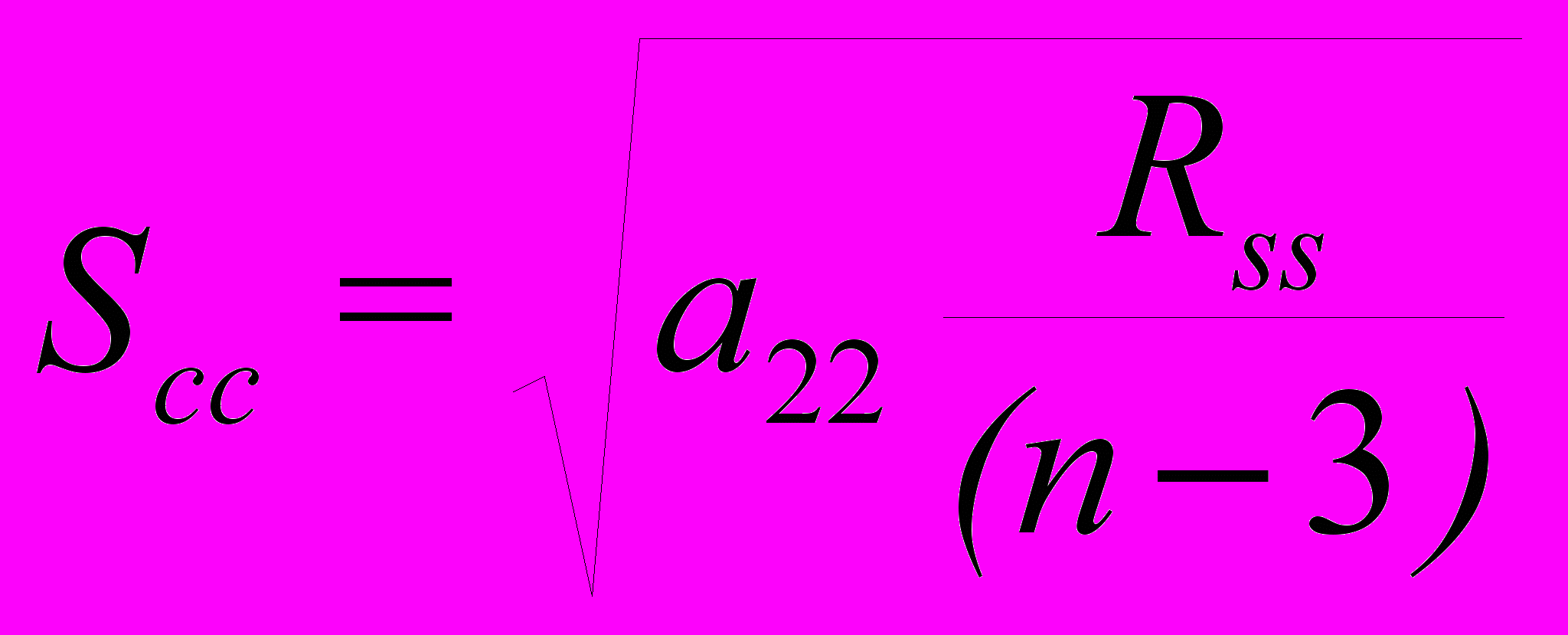и акрофазы: 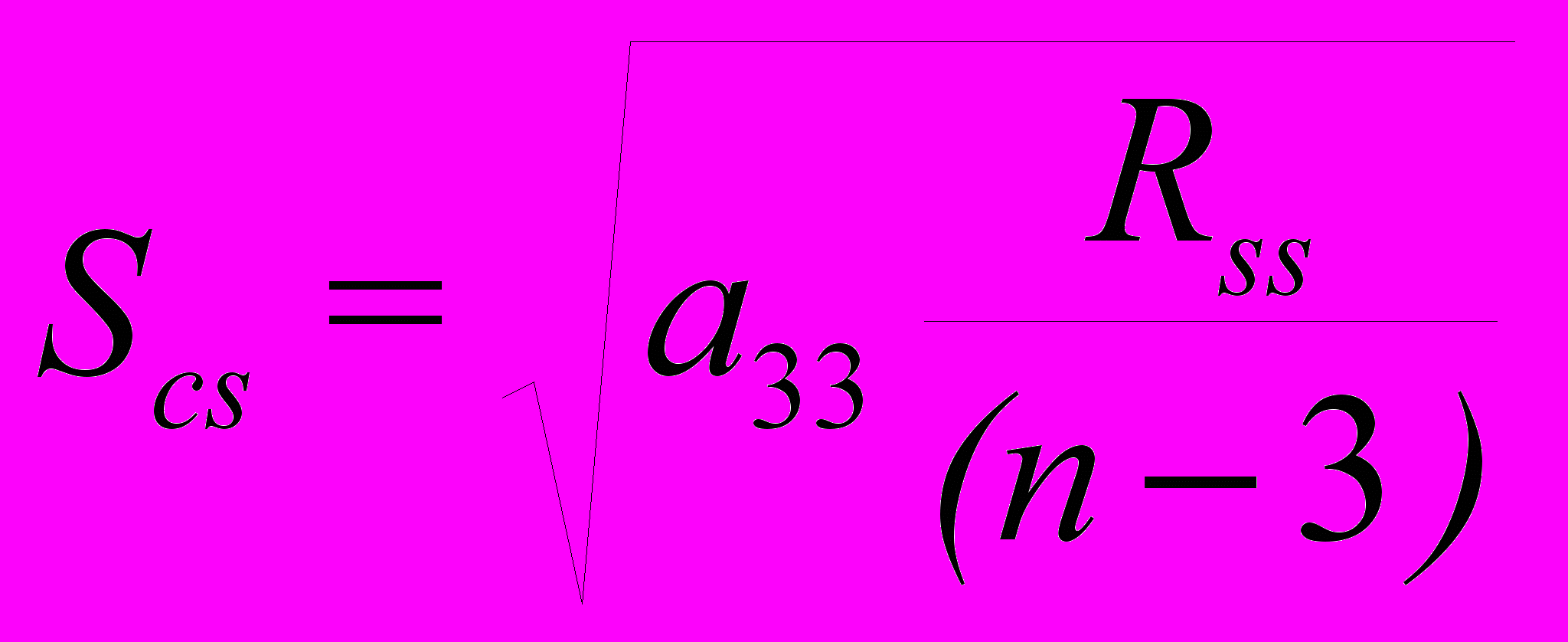. Значимость модели оценивается по t-критерию Стъюдента. Для его вычисления используется отношение амплитуды к стандартному отклонению амплитуды: 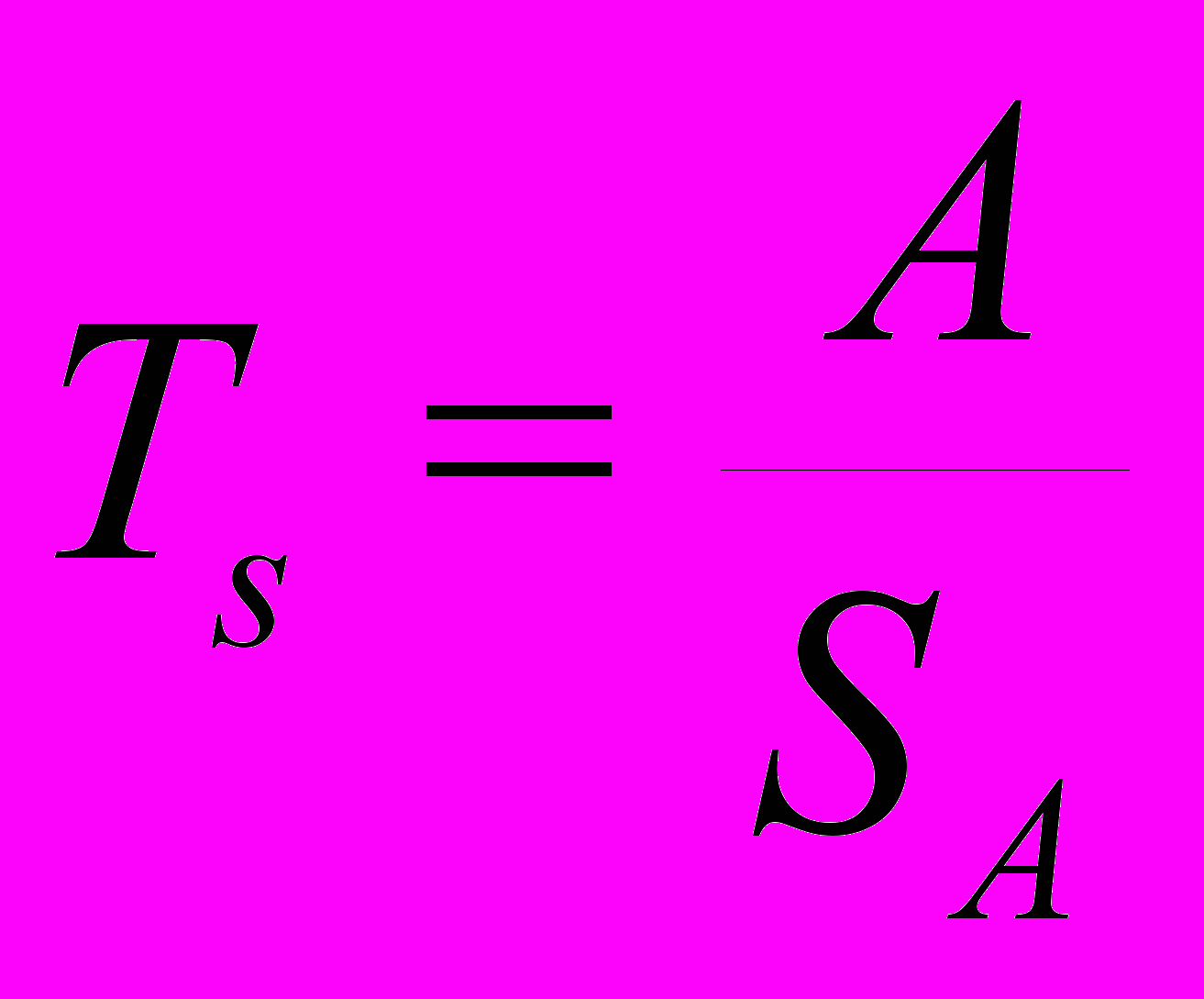. Само же стандартное отклонение рассчитывается по формуле:





П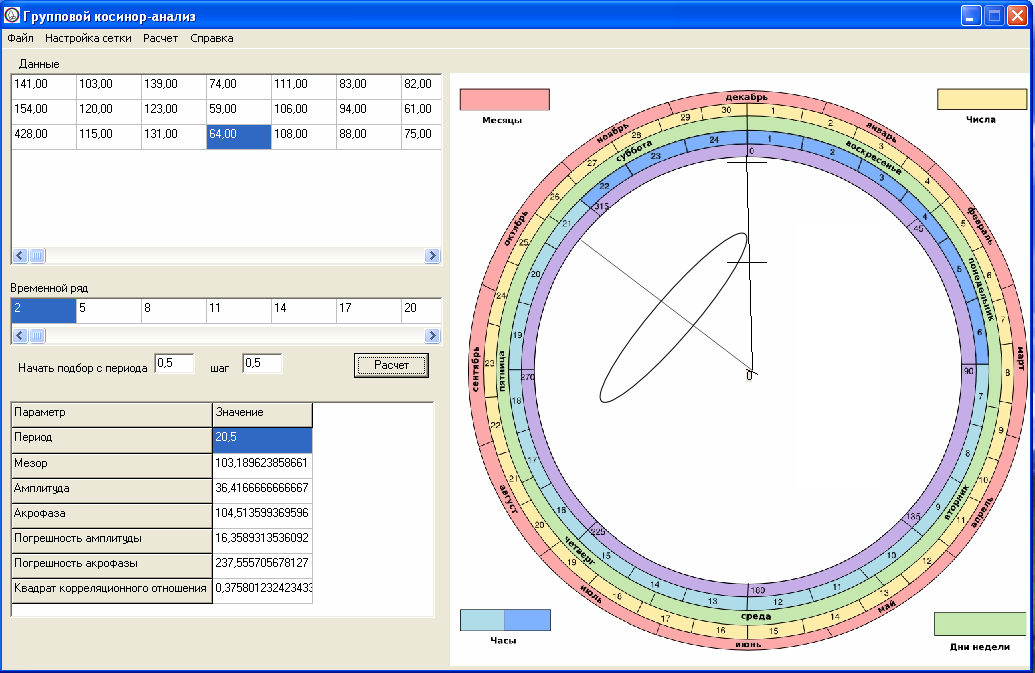редставленный алгоритм достаточно объемный и сложный для ручного выполнения. Поэтому он был реализован в программе «Групповой косинор-анализ», внешний вид которой представлен на рисунке 1.


Рис. 1. Главное окно программы "Групповой косинор-анализ"


Программирование осуществлялась в среде Delphi 7.0 Enterprise.

Программа предоставляет возможность как ручного ввода данных, так и автоматизированного забора массива хронограмм из MS Excel. Для ручного ввода предусмотрена регулировка параметров сетки. При автоматическом заборе данных сетка самостоятельно подстраивается под импортируемый массив чисел. Следует отметить что алгоритм требует особой формы ввода временного ряда. Отсчет времени должен производиться, начиная с момента исследования и до его окончания (например 2, 10, 18, 24, 32 часа и т.д.).

После ввода данных появляется возможность задать начальный период и шаг, с которым будут рассчитываться модели. По умолчанию они равны 0,5.

Затем становится доступна кнопка «расчет». Если все данные загружены корректно, запускается работа математического аппарата, результаты функционирования которого выводятся в специальной таблице. Сообщаются следующие параметры модели ритма: период ритма, мезор, амплитуда, акрофаза, погрешности амплитуды и акрофазы, коэффициент корреляции (t-критерий Стъюдента). По результатам расчетов программа строит доверительный эллипс в полярных координатах.





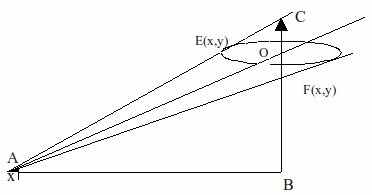
Рис. 2. Построение эллипса


Ниже представлена принципиальная схема построения такого эллипса и приведены формулы, задающие параметры построения. Сам контур эллипса рассчитывается, исходя из канонического уравнения.











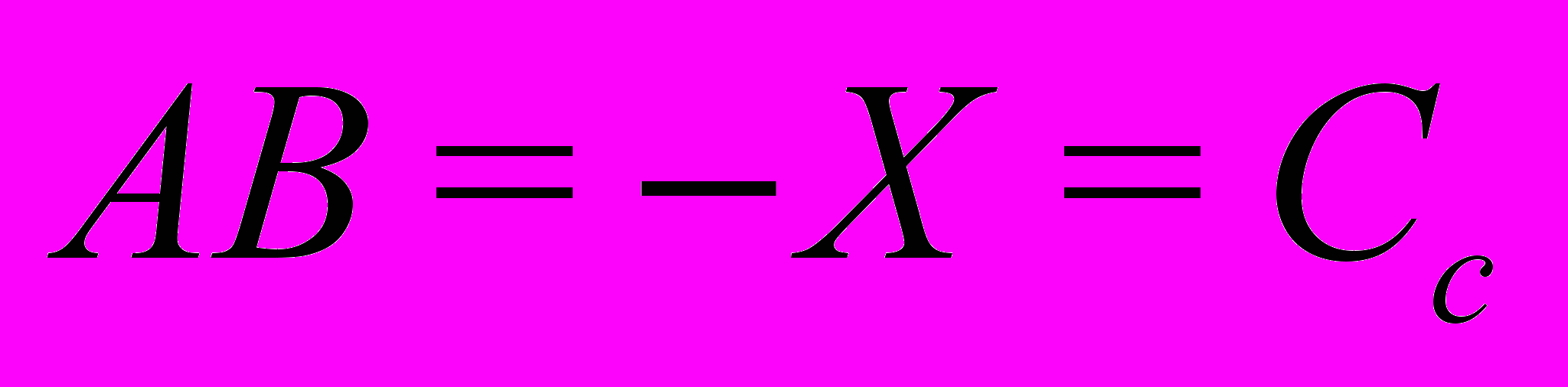
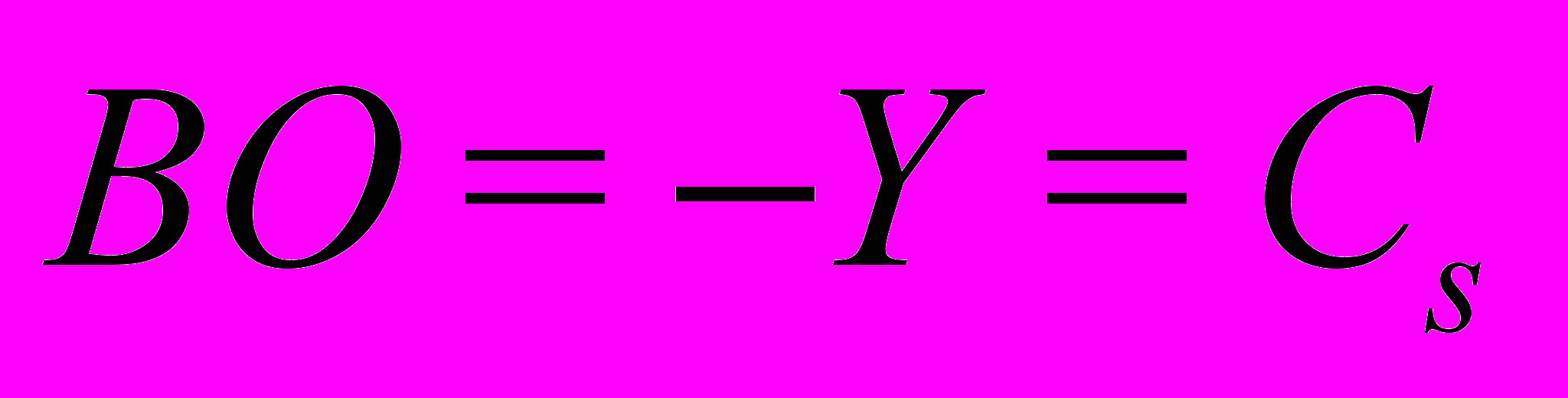
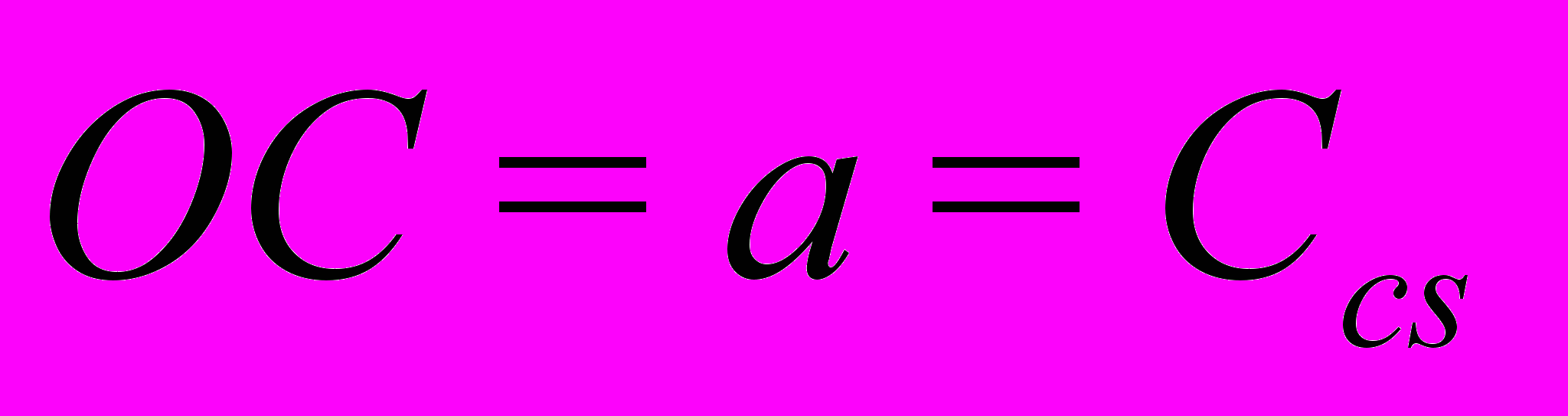
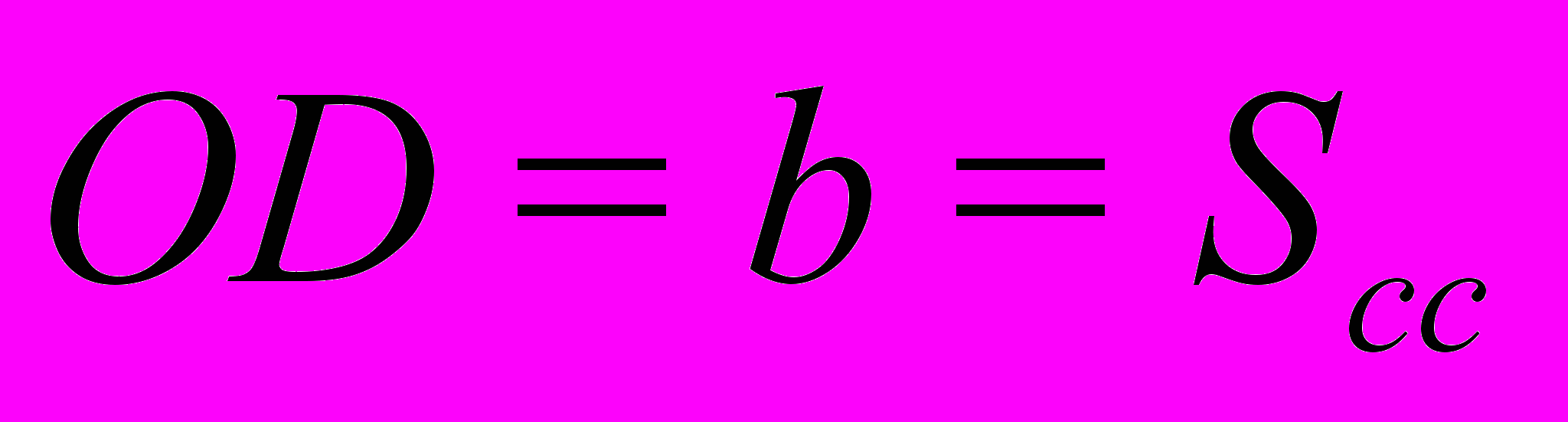
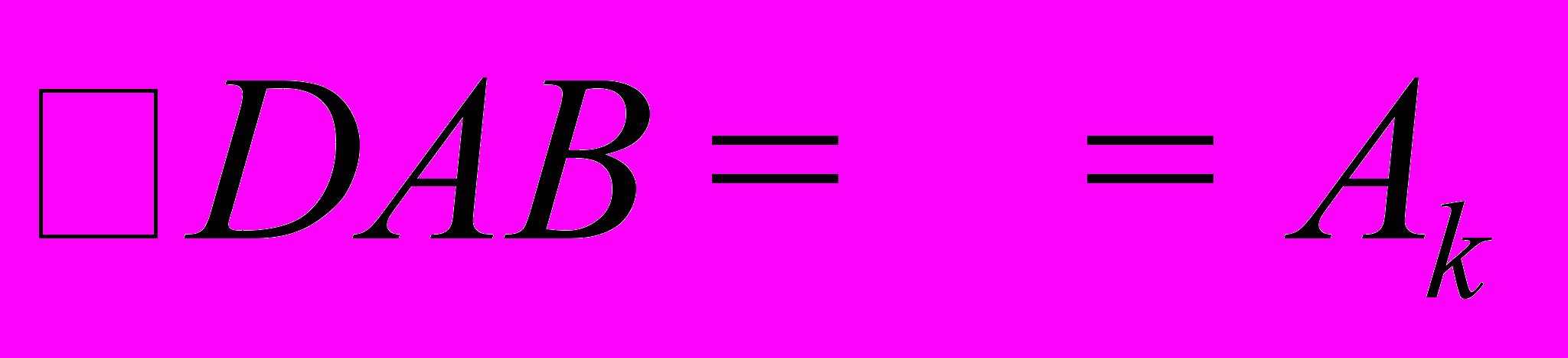
Полученная в итоге работы программа может использоваться как инструментальное средство при хронобиологических исследованиях, освобождая исследователя от трудоемких и громоздких вычислений, устраняя тем самым фактор человеческой ошибки и значительно сокращая время на обработку результатов.

Литература
  1. Бейли Н. Математика в биологии и медицине / Пер. с англ. Е.Г. Коваленко. – М.: МИР, 1970. – 327 с.
  2. Фаронов В.В. Delphi. Программирование на языке высокого уровня. – М.: Питер, 2005. – 639 с.
  3. Хронобиология и хрономедицина. Руководство / под ред. Ф.И. Комарова. – М.: Медицина, 1989. – 400 с.