[Текст]: научно-аналитический журнал (издаётся с 2007 г.)

Вид материала

Документы

Содержание В. Н. Самсонов, А. Г. Санников, О. А. Чуклеева ИНДИВИДУАЛИЗАЦИЯ МЕДИКАМЕНТОЗНЫХ НАЗНАЧЕНИЙ СРЕДСТВАМИ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВА Ключевые слова

Подобный материал:

• 9) [Текст]: научно-аналитический журнал (издаётся с 2007 г.), 9826.34kb.
• 11) [Текст]: научно-аналитический журнал (издаётся с 2007 г.), 3594.13kb.
• 10) [Текст]: научно-аналитический журнал (издаётся с 2007 г.), 5535.4kb.
• 8) [Текст]: научно-аналитический журнал серия «Право» (издаётся с 2007 г.), 15457.76kb.
• [Текст]: научно-аналити-ческий журнал (издаётся с 2007 г.), 4433.08kb.
• Мировой экономики, управления и права, 9699.86kb.
• Мировой экономики, управления и права, 4708.15kb.
• Анкета участника международной научно-практической конференции «актуальные проблемы, 62.51kb.
• Ежемесячный аналитический журнал, 26.94kb.
• Журнал издается с 1991, 2949.78kb.

В. Н. Самсонов, А. Г. Санников, О. А. Чуклеева

ИНДИВИДУАЛИЗАЦИЯ МЕДИКАМЕНТОЗНЫХ НАЗНАЧЕНИЙ

СРЕДСТВАМИ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ

ФАРМАКОКИНЕТИЧЕСКИХ ПРОЦЕССОВ

Аннотация: в статье рассматриваются фармакокинетические модели, предназначенные для индивидуального подбора дозы препарата с учетом индивидуальных особенностей больного. Также рассматривается программное обеспечение, описывающее данные модели.

Annotation: The article studies the pharmacokinetic patterns for an individual drug doze with regard to the patient’s individual characteristics. It also describes the software for the above-mentioned patterns.

Ключевые слова: фармакокинетика, информатизация в медицине, информатизация систем в здравоохранении, системы, поддерживающие принятие решения.

Key words: pharmacokinetics, informatization in medicine, informatization in healthcare, decision-making systems.


Степень математизации научных дисциплин служит объективной характеристикой глубины знаний об изучаемом предмете. Так, многие явления физики, химии, техники описываются математическими методами достаточно полно. В результате эти науки достигли высокой степени теоретических обобщений. В биологических науках математические методы пока еще играют подчиненную роль из-за сложности объектов, процессов и явлений, вариабельности их характеристики, наличия индивидуальных особенностей. Систематические попытки использовать математические методы (ММ) в биомедицинских направлениях начались в 80-х гг. 19 века.

Начиная с 40-х гг. 20 в. математические методы проникают в медицину и биологию через кибернетику и информатику. Наиболее развиты математические методы в биофизике, биохимии, генетике, физиологии, медицинском приборостроении, создании биотехнических систем. Благодаря математическим методам значительно расширилась область познания основ жизнедеятельности, и появились новые высокоэффективные методы диагностики и лечения. Все большую роль во внедрении ММ в медицину играют ЭВМ.

Одной из актуальных задач практической медицины является индивидуализация лекарственного лечения, поскольку многие параметры распределения и выведения лекарственных средств зависят от состояния конкретного больного.

Основной целью является разработка программного обеспечения, использующего фармакокинетические модели, способная упростить процесс подбора дозы лекарственного препарата.

При разработке системы применялись методы:

• Математического моделирования: камерные, бескамерные фармакокинетические модели.
  
• Программирование: программа написана на языке C# в среде Microsoft Visual Studio. Для запуска программы необходимо наличие платформы Microsoft .NET Framework 2.0.
  

Для обработки и интерпретации фармакокинетического эксперимента используют различные варианты математического моделирования. В так называемой камерной модели организм представлен как совокупность взаимосвязанных абстрактных частей (камер), между которыми и внутри которых происходят процессы распределения, метаболизма и выведения лекарственного вещества [3].

Наиболее простой фармакокинетической моделью является однокамерная модель, при которой организм представляется в виде единой гомогенной камеры (см. рис. 1). Эта модель пригодна для анализа концентрации препарата в крови, плазме и сыворотке, а также для анализа концентрации в моче лекарственных средств, которые быстро распределяются между плазмой крови и другими жидкостями и тканями организма.





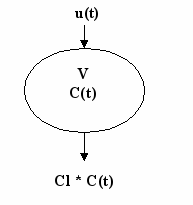
Рис. 1. Однокамерная модель


После поступления вещества в камеру в количестве D оно распределяется мгновенно и равномерно и занимает объем камеры, при этом концентрация вещества, которая создается в камере, обозначается как начальная концентрация С₀. Кажущийся объем распределения рассматривается как камера, куда препарат поступает со скоростью u(t), которая зависит от заданного лечащим врачом режима дозирования, и откуда препарат выводится со скоростью элиминации Cl*C(t).

Рассмотрим два последовательных момента времени t и t + h, где h – шаг по времени и t >= 0. Закон сохранения вещества может быть записан в математической форме в виде следующего уравнения:


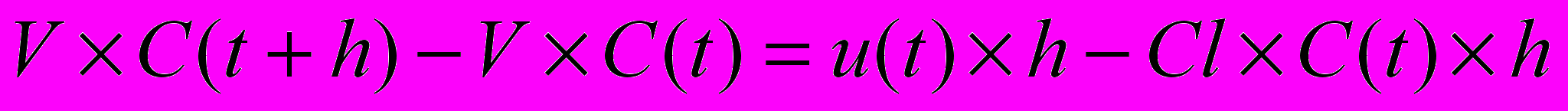, (1)


где V – объем распределения; C(t) – концентрация в момент времени t; u(t) – скорость введения препарата; Cl – клиренс.

Из уравнения (1) величина C(t+h) может быть выражена следующим образом:


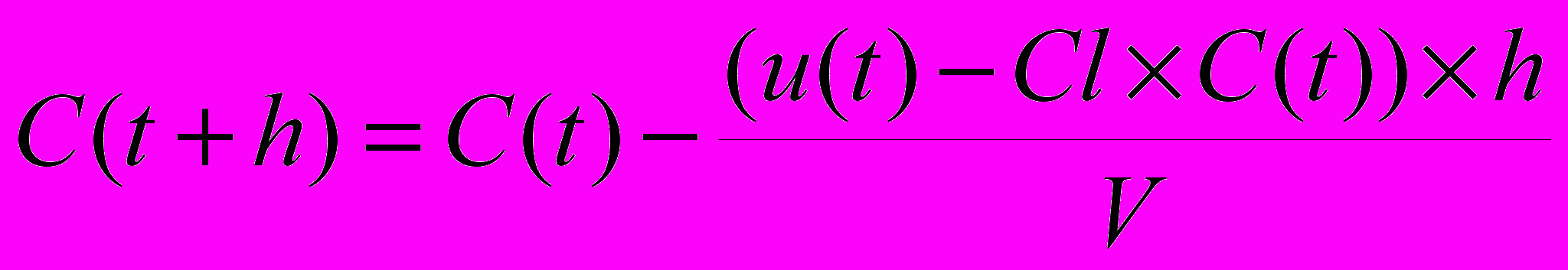, (2)


Данная модель предполагает, что любые изменения концентрации лекарственного средства в плазме отражают изменения его содержания в тканях. Распределение препаратов в однокамерной модели происходит быстро, вследствие чего вскоре устанавливается стационарное состояние, т.е. устойчивое динамическое равновесие между поступлением препарата в кровь и выходом из нее.

Более приемлемы двух- и трехкамерные модели. За центральную камеру принимают плазму крови, составляющие ее элементы, а так же сердце, легкие, печень, почки и эндокринные железы; за периферическую – мышцы, кожу, жир. В этих камерах лекарственное средство распределяется с разной скоростью: быстро – в центральной и медленно – в периферической, после чего частично выводится. Например, после внутривенного введения лекарственное вещество сначала быстро распределяется в центральной камере, в меньшей степени – в периферической камере и частично начинает выводиться из организма [1].

Так, например, двухкамерная модель (см. рис. 2) может описывать внутримышечное введение лекарственного вещества, где препарат сначала попадает в мышцу, а затем диффундирует из мышцы в кровь.




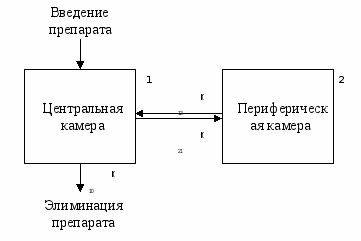
Рис. 2. Двухкамерная открытая модель. Константы k12 и k21 определяют

скорость перемещения лекарственного препарата между центральной

и периферическими камерами; k10 – константа скорости элиминации


Применяя закон сохранения массы к количеству лекарственного вещества, содержащегося в мышце, и к количеству лекарственного вещества в кажущемся объеме, получим 2 уравнения:


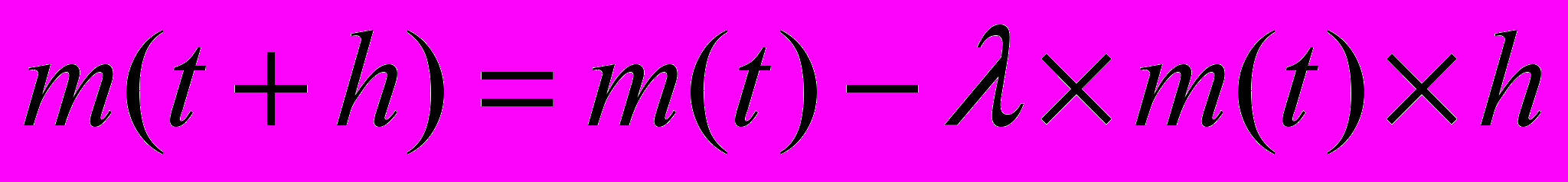, (3)

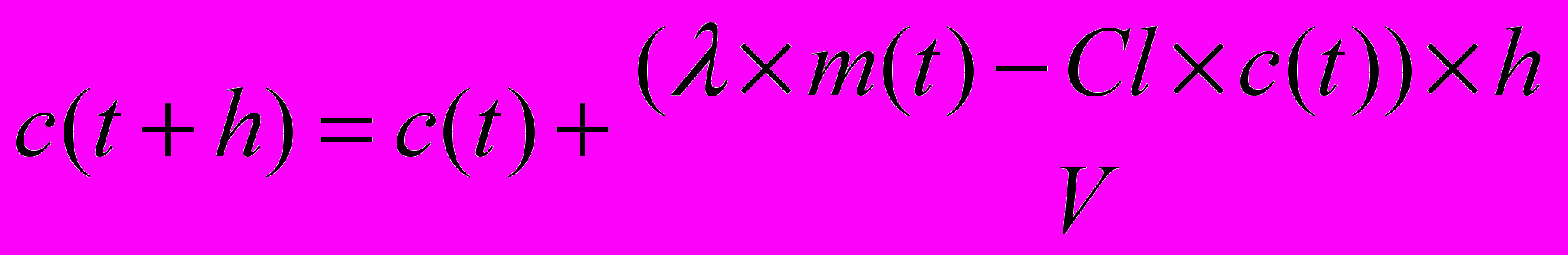, (4)


где m(t) – масса лекарственного вещества в мышце в данный момент времени; λ – коэффициент скорости диффузии препарата из мышцы в кровь; D – доза препарата.


При t = 0






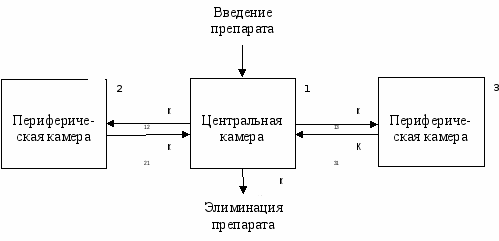
Рис. 3. Трехмерная открытая модель, состоящая

из центральной камеры 1 и периферических камер 2 и 3


Однако разработанные математические модели, которые представляют большое значение, практически не применяются на практике. В основном это связано с тем, что расчет индивидуального режима дозирования лекарственных препаратов осуществляется вручную и может занять много времени. Особенно, если нужно произвести расчет на длительный курс лечения.

Для того чтобы упростить процесс поиска нужного режима дозирования было разработано программное обеспечение, описывающее работу как камерных, так и бескамерных математических моделей. Тем самым значительно упрощается поиск нужного режима дозирования, а все вычисления выполняет ЭВМ.

В зависимости от выбранного способа ввода лекарственного препарата, предоставляется отдельная настройка модели, где лишь нужно указать необходимые значения и перейти к просмотру полученного результата. Если полученный результат, по каким либо причинам, не устраивает, то всегда можно вернуться к режиму настройки и подкорректировать модель, изменив нужные значения.

В программе предусмотрено два режима настройки: для одноразового ввода лекарственного препарата и многоразового, если курс лечения занимает много времени. Для настройки многоразового ввода нужно лишь будет дополнительно указать время, через которое будет повторно введено лекарство и продолжительность лечения. Таким образом, можно подобрать более удобный для медперсонала интервал введения. В случае необходимости графики курса лечения можно сохранить отдельно и распечатать.

В программе необходимо указать необходимые данные для расчета дозы лекарства. При выборе способа ввода подбирается нужная фармакокинетическая модель, которая описывает концентрацию препарата.

После настройки модели выводится график, где показан вывод лекарственного препарата после одноразового введения (см. рис. 4). На графике видна максимальная концентрация, а так же время, за которое препарат полностью выводится из организма.





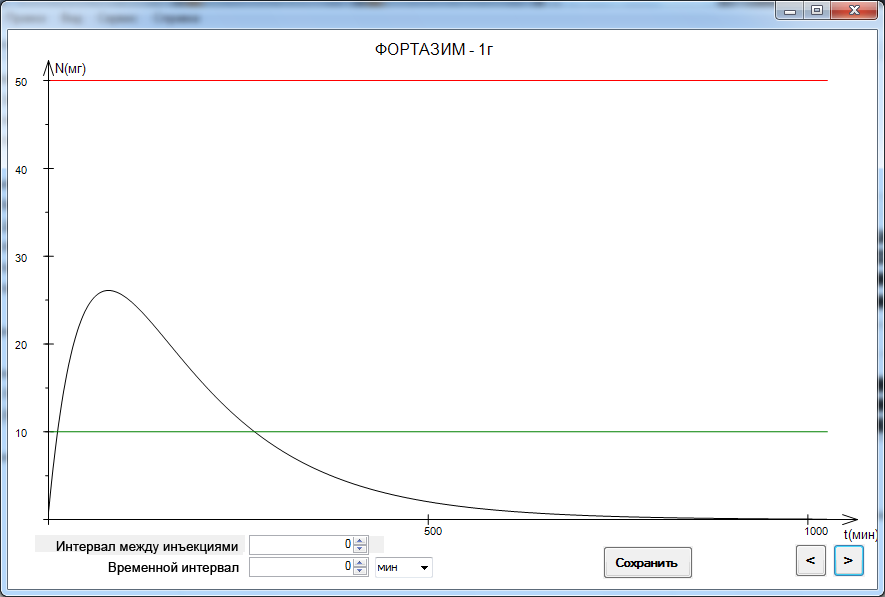
Рис. 4. Настройка модели для многократного введения лекарственного препарата


На основе анализа камерных и бескамерных моделей фармакокинетических процессов создана программа для ЭВМ, способная стать удобным инструментом повседневной деятельности врача по индивидуализации назначения лекарственных препаратов.

Литература

1. Ганцев Ш.Х., Рахматуллина И.Р., Танюкевич М.В. Использование методов математического моделирования в здравоохранении // Здравоохранение Российской Федерации. – 2003. – № 5. – С. 35-38.

2. Нэш Трей. C# 2008: ускоренный курс для профессионалов.: Пер. с англ. – М.: ООО "ИД Вильямс", 2008. – 576 с.: ил. – Парал. тит. англ.

3. Советов Б.Я., Яковлев С.А. Моделирование систем: Учебник для вузов – 3-е изд., перераб. и доп. – М.: Высш. шк., 2001. – 343 с.;