На включение программы повышения квалификации педагогических и руководящих работников муниципальных общеобразовательных учреждений Воронежской области в региональный банк программ
| Вид материала | Программа |
- На включение программы повышения квалификации педагогических и руководящих работников, 198.87kb.
- На включение программы повышения квалификации педагогических и руководящих работников, 370.56kb.
- На включение программы повышения квалификации педагогических и руководящих работников, 188.42kb.
- На включение программы повышения квалификации педагогических и руководящих работников, 224.72kb.
- На включение программы повышения квалификации педагогических и руководящих работников, 157kb.
- На включение программы повышения квалификации педагогических и руководящих работников, 169.75kb.
- На включение программы повышения квалификации педагогических и руководящих работников, 359.12kb.
- На включение программы повышения квалификации педагогических и руководящих работников, 231.22kb.
- На включение программы повышения квалификации педагогических и руководящих работников, 465.46kb.
- На включение программы повышения квалификации педагогических и руководящих работников, 409.35kb.
Заявка
на включение программы повышения квалификации
педагогических и руководящих работников муниципальных
общеобразовательных учреждений Воронежской области в
региональный банк программ
ГОУ ВПО «Воронежский государственный педагогический университет»
ПРОГРАММА КУРСОВ ПОВЫШЕНИЯ
КВАЛИФИКАЦИИ УЧИТЕЛЕЙ МАТЕМАТИКИ
ПРОГРАММА для учителей математики общеобразовательных классов
ПО НАПРАВЛЕНИЮ: теоретические и практические основы обучения математике
Титульный лист заявки
Наименование учреждения: ГОУ ВПО «Воронежский государственный педагогический университет»
Наименование учредителя учреждения: Министерство образования и науки РФ
№ и дата лицензии на право ведения образовательной деятельности по программам повышения квалификации: Серия А № 282047 от 17 марта 2008 г.
№ и дата свидетельства о государственной аккредитации программ повышения квалификации: Серия АА № 001267, регистрационный, № 1237 от 28 апреля 2008 г., срок действия до 28 апреля 2013 года
Наименование программы с указанием категории слушателей:
Программа курсов повышения квалификации учителей математики общеобразовательных классов
_______________________________________________________________________________
_______________________________________________________________________________
Объем (в часах) _170 час, из них 72 (инвариантная), 24 часа (вариативная)_______
Стоимость курса обучения в расчете на одного слушателя: _____________________________________________________________________________
ФИО ректор учреждения: Потапов А.С.
ФИО, должность разработчика программы повышения квалификации: _Беляева Э.С., к.п.н, доцент кафедры информатики и МПМ, Бондаренко Т.Е., к.п.н., доцент кафедры информатики и МПМ, Титоренко С.А., к.п.н., доцент кафедры информатики и МПМ, Гордиенко Н.А., к.ф.-м.н., доцент кафедры алгебры и геометрии, Капленко Э.Ф., к.ф.-м.н., доцент кафедры алгебры и геометрии
Юридический адрес учреждения: 394043, г. Воронеж, ул. Ленина, д.86.
Контактные адреса и телефоны учреждения: 54-56-43, 55-54-46,
e-mail: rektorat@vspu.ac.ru
Перечень приложений к заявке: (если есть)_________________________________________________________________________
______________________________________________________________________________________________________________________________________________________
Подпись ректора:
(печать)
ПРОГРАММА КУРСОВ ПОВЫШЕНИЯ КВАЛИФИКАЦИИ
УЧИТЕЛЕЙ МАТЕМАТИКИ
ОБЩЕОБРАЗОВАТЕЛЬНЫХ КЛАССОВ
Пояснительная записка
Курсы предназначены для учителей математики общеобразовательных классов, в том числе ведущих элективные курсы.
Цели курсов.
Содействие совершенствованию базовой и специальной профессиональной компетентностей учителей математики, обеспечивающих готовность к квалификационному обучению школьников математике.
Задачи курсов (в логике традиционного подхода).
- Углубить и систематизировать знания слушателей по математике и методике её преподавании; способствовать преодолению затруднений, возникающих в профессиональной деятельности;
- познакомить учителей с передовым педагогическим опытом в области применения новых технологий обучения математике, в том числе информационных;
- значительное внимание уделить содержательной стороне ГИА и ЕГЭ; организовать систему обучения решению задач повышенной сложности из контрольно-измерительных материалов ГИА и ЕГЭ по математике;
- приоритетно рассматривать методические аспекты школьного курса математики.
Задачи курсов (в логике компетентностного подхода).
Уровень ключевых компетентностей.
- Сформировать умение организовывать совместную деятельность с коллегами;
- проводить анализ своей интеллектуальной и педагогической деятельности.
Уровень базовых компетентностей.
- Сформировать у слушателей:
1) систему современных математических знаний;
2) умение обеспечивать квалифицированное методическое сопровождение процесса обучения математике, в том числе ИКТ в насыщенной среде;
3) мотивировать самообразовательную деятельность слушателей в области обучения математике.
Уровень специальных компетентностей.
- Сформировать умение осуществлять экспертизу содержательной и технологической характеристик современных методов обучения математике, в том числе с использованием ИКТ.
- Сформировать умение управлять деятельностью школьников на уроках математики, проводимых с использованием современных технологий обучения.
Особенностью программы курса является модульное построение.
Результаты освоения программы курсов повышения квалификации.
Уровень ключевых компетентностей:
- комплекс умений, необходимых для организации совместной деятельности с коллегами;
- повышение уровня аналитической компетентности.
Уровень базовых компетентностей:
- система современных математических знаний;
- комплекс профессиональных умений, обеспечивающих квалифицированное методическое сопровождение процесса обучения математике, в том числе ИКТ в насыщенной среде;
- сформированность мотивов самообразования слушателей в области обучения математике.
Уровень специальных компетентностей:
- умение осуществлять экспертизу содержательной и технологической характеристик современных методов обучения математике, в том числе с использованием ИКТ;
- умение управлять деятельностью школьников на уроках математики, проводимых с использованием современных технологий обучения;
- умение оценивать и диагностировать уровень освоения школьниками математики.
Условия реализации программы повышения квалификации. Курсы планируется проводить на базе лаборатории ЦОР и педагогического проектирования ВГПУ, а также других учебных аудиторий, имеющих специальное оборудование: электронная доска; проектор; ноутбук, персональные компьютеры; наборы ЦОР.
Использование новых форм и методов образовательного процесса.
В рамках программы повышения квалификации будут использованы следующие методы и технологии:
кооперативные техники, требующие объединения локальных инициатив слушателей; метод проектов; методика взаимообмена заданиями; деловые игры; портфолио.
К ведению занятий планируется привлечение как опытных учителей, так и учителей-новаторов.
Модуль №1
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И
МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Цели. Совершенствование подготовки слушателей в той области математики, которая изучает теорию вероятностей, а также ознакомление с методическими приемами решения некоторых задач теории вероятностей.
Учебно-тематический план
| № | Тема | Кол-во часов | Форма занятия |
| 1 | Комбинаторика. Решение комбинаторных задач | 6 | 2 лекции, практическое занятие |
| 2 | Основы теории вероятностей и математической статистики | 6 | 2 лекции, практическое занятие |
| 3 | Использование ЦОР в процессе изучения основ теории вероятностей и математической статистики в школе | 2 | лекция |
| | Итого | 14 часов | |
Содержание тем
1. Комбинаторика. Решение комбинаторных задач
Понятие выборки элементов, общие правила комбинаторики. Комбинаторные принципы сложения и умножения. Основные формулы и их использование при решении задач о числе размещений, перестановок, сочетаний (без повторений и с повторениями). Задачи, связанные с биномиальной формулой Ньютона.
2. Основы теории вероятностей и математической статистики
Изучение вероятностно-статистической линии в школьном курсе математики. Введение понятия случайного события и операций над ними. Различные подходы к определению вероятности, частота события. Операции над вероятностями, формула полной вероятности. Независимые повторные испытания (схема Бернулли). Дискретные случайные величины, их распределения и числовые характеристики. Методы статистического анализа.
3. Использование ЦОР в процессе изучения основ теории вероятностей и математической статистики в школе
Использование Интернет-ресурсов. ссылка скрыта , ссылка скрыта, ссылка скрыта .
Формы контроля:
– тестирование слушателей;
– разработка рабочих программ обязательных уроков и элективных курсов на основе изученного материала;
– самостоятельные работы;
– рефераты и доклады на основе опыта собственной работы с учащимися.
Модуль № 2
МЕТОДИЧЕСКИЕ И СОДЕРЖАТЕЛЬНЫЕ АСПЕКТЫ ОБУЧЕНИЯ ТОЖДЕСТВЕННЫМ ПРЕОБРАЗОВАНИЯМ В КУРСЕ МАТЕМАТИКИ СРЕДНЕЙ ШКОЛЫ
Цели. 1) Изложить методические приемы обучения тождественным преобразованиям и методику формирования умения применять их как средство рационализации вычислений. 2) Рассмотреть тождественные преобразования в процессе решения уравнений.
Учебно-тематический план
| № | Тема | Кол-во часов | Форма занятий |
| 1. | Роль тождественных преобразований в процессе рационализации вычислений. | 1 | Лекция |
| 2. | Методические аспекты обучения тождественным преобразованиям с целью их применения для рационализации вычислений (на примере вынесения общего множителя за скобки) | 2 | Лекция |
| 3. | Система действий поиска и реализации рациональной вычислительной программы и её формирование у учащихся. | 2 | Лекция |
| 4. | Тождественные преобразования в процессе решения уравнений. | 2 1 | Лекция Практ.занятие |
| | Итого | 8 | |
Содержание тем
1. Роль тождественных преобразований в процессе рационализации вычислений.
Функциональный и алгоритмический подход к понятию тождественного преобразования. Тождественное преобразование как средство поиска рациональной вычислительной программы.
2. Методические аспекты обучения тождественным преобразованиям с целью их применения для рационализации вычислений (на примере вынесения общего множителя за скобки).
Методическая система обучения тождественным преобразованиям с целью их применения для рационализации вычислений.
3. Система действий поиска и реализации рациональной вычислительной программы и её формирование у учащихся.
Методика формирования системы действий поиска и реализации рациональной вычислительной программы.
4. Тождественные преобразования в процессе решения уравнений.
Тождественные преобразования, изменяющие область определения уравнения (приведение подобных слагаемых, сокращение дробей, действия с корнями и логарифмами, некоторые формулы тригонометрии). Средства регулирования области определения уравнения, предотвращающие появление посторонних корней или их потерю. Комплекс уравнений.
Формы контроля:
- реализация методики на примере (разработка комплекса упражнений для обучения отдельному тождественному преобразованию и его применению для рационализации вычислений);
- комплекс уравнений, при решении которых выполняются тождественные преобразования, приводящие к появлению посторонних корней или их потере. Анализ процесса решения.
Модуль №3
УРАВНЕНИЯ И НЕРАВЕНСТВА В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ: РАВНОМЕРНОСТЬ И МЕТОДЫ РЕШЕНИЯ
Цель. Познакомить слушателей с теорией равносильности структур (уравнений, неравенств, их систем и совокупностей) и обосновать основные приёмы решения уравнений и неравенств курса математики средней школы.
Учебно-тематический план
| № | Тема | Кол-во часов | Форма занятия |
| 1. | Различные определения равносильности уравнений (неравенств, систем, совокупностей уравнений и неравенств) | 2 | лекция |
| 2. | Теория равносильности уравнений (неравенств) по П.А.Буданцеву | 4 | лекции |
| 3. | Анализ школьных учебников по алгебре, алгебре и началам анализа | 2 | практическое занятие |
| 4. | Основные приёмы решения уравнений, неравенств и их систем в курсе алгебры основной школы | 4 | 2 - лекция 2 - практическое занятие |
| 5. | Основные приёмы решения уравнений, неравенств и их систем в курсе алгебры и начал анализа (10-11 кл.) | 4 | 2 - лекция 2 - практическое занятие |
| 6. | Уравнения, неравенства и их системы в материалах ЕГЭ по математике (уровень С) | 4 | 2 - лекция 2 - практическое занятие |
| | ИТОГО | 20 часов | |
Содержание тем
1. Различные определения равносильности уравнений (неравенств, систем, совокупностей уравнений и неравенств).
Различные трактовки понятия равносильности уравнений, неравенств и их систем (по С.Н.Новосёлову, В.Г.Болтянскому, П.А.Буданцеву). Сравнительный анализ им соответствующих теорий.
2. Теория равносильности уравнений (неравенств) по П.А.Буданцеву
Теория равносильности по П.А.Буданцеву: теорему равносильности уравнений; неравенств; систем уравнений (неравенств); совокупностей уравнений (неравенств). Доказательство теорем и иллюстрация примерами.
3. Анализ школьных учебников по алгебре, алгебре и началам анализа.
Анализ теоретической и практической частей школьных учебников по алгебре, алгебре и началам анализа в различные периоды 20-21 веков (40-50 годы 20 века, 50-60 годы 20 века, 60-70 годы 20 века, 70-80 годы 20 века, 80-90 годы 20 века; с 2000 г. по настоящее время).
4. Основные приёмы решения уравнений, неравенств и их систем в курсе алгебры основной школы.
Выявление основных видов уравнений, неравенств и их систем по каждому из 7-9 классу и оформление решения базовых с полным обоснованием (ссылками на теоремы равносильности по П.А.Буданцеву.
5. Основные приёмы решения уравнений, неравенств и их систем в курсе алгебры и начал анализа (10-11 кл.)
Решение основных видов уравнений, неравенств и их систем из различных пособий курса алгебры и начал анализа общеобразовательных классов с обоснованием.
Формы контроля:
- оформление теоретических карт по теме «Теория Б-равносильности уравнений, неравенств, систем уравнений, совокупности уравнений»;
- образцы обоснованных решений базовых упражнений (уравнений и неравенств) по курсу алгебры (алгебры и начал анализа) одного из классов (7-11).
Модуль № 4
АЛГЕБРА И ГРАФИКА МОДУЛЯ
Цели. 1) Способствовать углублению и систематизации подготовки слушателей по темам модуля. 2) Обеспечить их дидактическими материалами для работы с учащимися и методическими рекомендациями к ним.
Учебно-тематический план
| № | Тема | Количество часов | Форма занятий |
| 1. | Определение и свойства модуля. Методы решения уравнений и неравенств с модулем. | 2 2 | Лекция Практическое занятие |
| 2. | Модули и корни. | 1 | Лекция |
| 3. | Модуль как средство регулирования области определения. | 1 | Лекция |
| 4. | Приёмы построения графиков с модулем. | 2 | Лекция |
| 5. | Применение приёмов построения графиков с модулем при решении задач. | 2 | Практическое занятие |
| | Итого | 10 часов | |
Содержание тем
1. Определение и свойства модуля. Методы решения уравнений и неравенств с модулем.
Понятие модуля: определение и свойства. Методы решения уравнений и неравенств с модулем, основанные на его определении, свойствах, графической интерпретации. Метод интервалов. Система упражнений на применение рассмотренных методов. Задания из контрольно-измерительных материалов ЕГЭ.
2. Модули и корни.
Понятие арифметического корня. Взаимосвязь между арифметическим корнем и модулем. Система упражнений на применение модуля в процессе преобразования корней. Задания из контрольно-измерительных материалов ГИА и ЕГЭ.
3. Модуль как средство регулирования области определения.
Модуль как средство, влияющее на область определения уравнения или неравенства. Примеры использования модуля в процессе решения уравнений и неравенств различных видов. Комплекс заданий.
4. Приёмы построения графиков с модулем.
Алгоритмы построения графиков, содержащих модуль:
 ,
,  ,
, 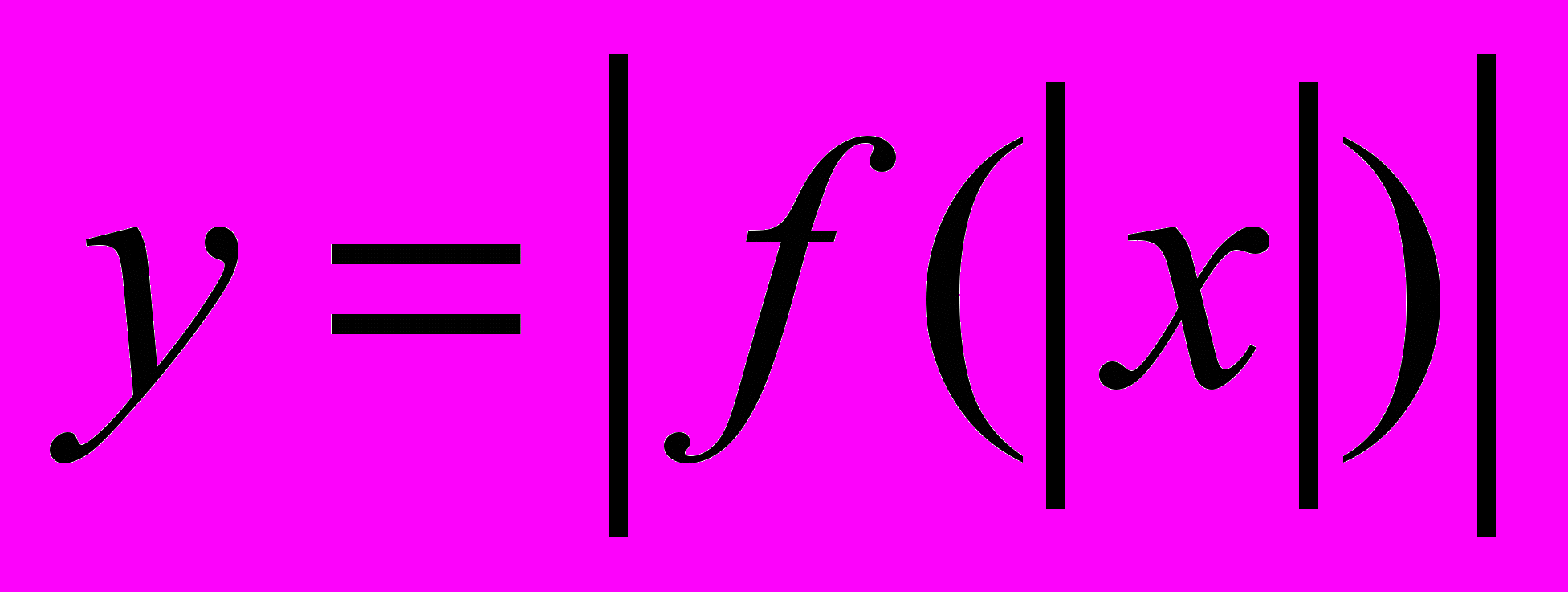 ,
,  .
. 5. Применение приёмов построения графиков с модулем при решении задач.
Комплексы упражнений, в которых рассмотренные приемы используются при решении уравнений и неравенств графическим методом при построении множеств точек плоскости, в заданиях с параметром.
