На включение программы повышения квалификации педагогических и руководящих работников муниципальных общеобразовательных учреждений Воронежской области в региональный банк программ
| Вид материала | Программа |
- На включение программы повышения квалификации педагогических и руководящих работников, 198.87kb.
- На включение программы повышения квалификации педагогических и руководящих работников, 370.56kb.
- На включение программы повышения квалификации педагогических и руководящих работников, 188.42kb.
- На включение программы повышения квалификации педагогических и руководящих работников, 224.72kb.
- На включение программы повышения квалификации педагогических и руководящих работников, 157kb.
- На включение программы повышения квалификации педагогических и руководящих работников, 169.75kb.
- На включение программы повышения квалификации педагогических и руководящих работников, 359.12kb.
- На включение программы повышения квалификации педагогических и руководящих работников, 231.22kb.
- На включение программы повышения квалификации педагогических и руководящих работников, 465.46kb.
- На включение программы повышения квалификации педагогических и руководящих работников, 409.35kb.
Формы контроля:
Домашняя контрольная работа. Её содержание представлено
- в пособии [7], в разделах «Упражнения для самостоятельной работы»,
№ 10 - №33 (с. 9 - 11); № 39 - №45, (с. 13 - 14); № 48 (с. 16); № 52 - №83 (с. 19 - 24); № 87 - №97 (с. 27 - 28);
- в пособии [12] № 8.157 - №8.178 (с. 105 - 106); № 10 - №33 (с. 9 - 11);
№ 9.25 - № 9.78 (с. 114 - 116);
Модуль № 5
УРАВНЕНИЯ И НЕРАВЕНСТВА С ПАРАМЕТРОМ
Цели. 1) Познакомить слушателей с основными понятиями темы: классификацией уравнений, неравенств, их систем и совокупностей с параметром, а также методов их решения. 2) Раскрыть особенности методики изучения данной темы в курсе математики средней школы.
Учебно-тематический план
| № | Тема | Кол-во часов | Форма занятий |
| 1. | Основные понятия. Классификация уравнений с параметром и методов их решения | 2 | Лекция |
| 2. | Линейные и квадратные уравнения, неравенства, их системы и совокупности с параметром | 2 | Лекция |
| 3. | Другие виды уравнений, неравенств, их систем и совокупностей с параметром. Аналитический метод их решения | 6 | Практические занятия |
| 4. | Уравнения, неравенства, их системы и совокупности с модулем и параметром | 3 | 1 - лекция 2 - практ. зан. |
| 5. | Графический метод решения задач с параметром | 4 | 2 - лекция 2 - прак. зан. |
| 6. | Задачи с параметром в материалах ГИА и ЕГЭ по математике | 2 | лекция |
| 7. | Контрольная работа | 1 | прак. занят. |
| | Итого | 20 часов | |
Содержание тем
1. Основные понятия. Классификация уравнений с параметром и методов их решения.
Основные понятия: параметр; уравнение (неравенство) с параметром; область определения уравнения (неравенства) с параметром; решение уравнения (неравенства) с параметром; что значит решить уравнение (неравенство) с параметром; уравнение - следствие; равносильность уравнений (неравенств). Классификация уравнений (неравенств) с параметром: линейные, квадратные, дробно-рациональные, тригонометрические, иррациональные, показательные, логарифмические. Системы и совокупности уравнений (неравенств) с параметром. Ось параметра и графическая иллюстрация ответа. Методы решения задач с параметром: аналитический, графический, координатно-параметрический.
2. Линейные и квадратные уравнения, неравенства, их системы и совокупности с параметром.
Основные понятия: линейные и квадратные уравнения (неравенства) с параметром. Линейные уравнения (неравенства) без ветвлений и с ветвлениями. Квадратные уравнения (неравенства) с параметром. Системы и совокупности линейных и квадратных уравнений и неравенств с параметром. Уравнения (неравенства), сводимые к линейным и квадратным.
3. Другие виды уравнений, неравенств, их систем и совокупностей с параметром. Аналитический метод их решения.
Дробно-рациональные, иррациональные, тригонометрические, показательные, логарифмические уравнения (неравенства с параметром), их системы и совокупности. Аналитический метод их решения. Ось параметра и графическая иллюстрация ответа: их использование при решении задач с параметром с дополнительными условиями. Комбинированные уравнения (неравенства) с параметром, их системы и совокупности.
4. Уравнения, неравенства, их системы и совокупности с модулем и параметром.
Применение различных методов решения уравнений (неравенств) с модулем к задачам с параметром. Линейные, квадратные, дробно-рациональные, иррациональные, тригонометрические, показательные, логарифмические уравнения (неравенства) с модулем и параметром, их системы и совокупности. Комбинированные уравнения (неравенства) с модулем и параметром, их системы и совокупности.
5. Графический метод решения задач с параметром.
Азбука элементарных функций и её использование при изучении данной темы. Линейная и квадратичная функции с параметром. Подготовительные упражнения. Решение уравнений (неравенств) с параметром, их систем и совокупностей в различных системах координат: (хОу), (аОх), (хОа). Координатно-параметрический метод. Примеры решения задач с параметром основных видов в соответствии с приведённой ранее классификацией графическим методом.
6. Задачи с параметром в материалах ГИА и ЕГЭ по математике.
Анализ содержания и методов решения задач с параметром ГИА и ЕГЭ по математике. Методические рекомендации по ознакомлению учащихся с темой «Задачи с параметром». Решение некоторых задач из материалов ГИА и ЕГЭ по математике.
7. Контрольная работа.
В её содержание включаются уравнения, неравенства, их системы и совокупности с параметром различных видов.
Формы контроля:
- теоретические карты по темам 1-5;
- контрольная работа.
Модуль № 6
ОБУЧЕНИЕ РЕШЕНИЮ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ НА ОСНОВЕ ТЕОРЕТИЧЕСКИХ КАРТ
Цели. 1) Познакомить слушателей с методом обучения решению геометрических задач на основе теоретических карт. 2) Представить содержательное и методическое обеспечение метода.
Учебно-тематический план
| № | Тема | Количество часов | Форма занятий |
| 1. | Характеристика метода. Теоретические карты по темам «Подобные треугольники», «Пропорциональные отрезки» и задачи к ним. | 1 2 | Лекция Практическое занятие |
| 2. | Теоретические карты по темам «Окружность», «Биссектрисы углов треугольника», «Медианы треугольника» и задачи к ним. | 1 2 | Лекция Практическое занятие |
| 3. | Теоретические карты по темам «Треугольник и окружность», «Площадь треугольника» и задачи к ним. | 1 2 | Лекция Практическое занятие |
| 4. | Теоретические карты по темам «Четырёхугольники», «Трапеция и параллелограмм» и задачи к ним. | 1 2 | Лекция Практическое занятие |
| 5. | Примеры теоретических карт по отдельным темам стереометрии «Параллельность в пространстве», «Перпендикулярность в пространстве», «Углы между прямыми и плоскостями» и их задачное обеспечение. | 4 4 | Лекция Практическое занятие |
| | Итого | 20 | |
Содержание тем
Каждая из перечисленных тем включает анализ теоретических карт, в которых компактно и наглядно представлены сведения, полезные при решении задач. Содержание таких сведений подобрано из школьных учебников и других источников. Рассматриваются доказательства утверждений, содержащихся в теоретических картах. Если они имеются в школьных учебниках, то приводятся ссылки на них.
Все карты обеспечены комплексами задач, которые сопровождаются чертежами, планами (алгоритмами) решений и ответами. Они подобраны так, чтобы каждое из теоретических утверждений было задействовано. Значительное внимание уделено задачам из контрольно-измерительных материалов единого государственного экзамена.
Формы контроля:
- разработка комплекса задач к отдельной теоретической карте, представление его с чертежами и алгоритмами решений.
Модуль №7
МЕТОД ДОПОЛНИТЕЛЬНЫХ ПОСТРОЕНИЙ (МЕТОД ДП) РЕШЕНИЯ ПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ
Цели. 1)Познакомить слушателей с принципом использования дополнительного построения определенного типа в задач с его характерными признаками. 2) Раскрыть методику обучения школьников решению задач курса планиметрии средней школы методом ДП.
Учебно-тематический план
| № | Тема | Кол-во часов | Форма занятия |
| 1. | Типизация дополнительных построений на чертежах плоских фигур (20 ДП) | 2 | лекция |
| 2. | Анализ текстовых задач учебника Л.С.Атанасяна (геометрия 7-9) | 2 | лекция |
| 3. | Набор задач, для решения которых используемый метод наиболее эффективен | 8 | 2 - лекция 6 - практические занятия |
| | Всего: | 12 часов | |
Содержание тем
1. Типизация дополнительных построений на чертежах плоских фигур (20 ДП).
Понятие дополнительного построения в методе. Дополнительное построение (ДП) на чертеже плоской фигуры как метод решения планиметрических задач. Основные типы дополнительных построений на чертежах плоских фигур (20 ДП).
2. Анализ текстовых задач учебника Л.С.Атанасяна (геометрия 7-9).
Выявление свойств фигур, характерных для соответствующего типа ДП. Иллюстрация на конкретных примерах из учебника Л.С.Атанасяна (геометрия 7-9).
3. Набор задач, для решения которых используемый метод наиболее эффективен
Авторская демонстрация сборника задач, для решения которых метод ДП наиболее эффективен. Решение задач.
Формы контроля:
- Разработка слушателями раздаточного материала для учащихся в виде карточек с дополнительными построениями.
- Поиск в журнале «Математика» (приложение к газете «Первое сентября») задач курса планиметрии, решаемых с помощью методы ДП. Оформление решений и сообщение их на практическом занятии (защита).
Модуль №8
ТРИГОНОМЕТРИЯ В КУРСЕ МАТЕМАТИКИ СРЕДНЕЙ ШКОЛЫ
Цели. 1) Дополнить и систематизировать знания слушателей по тригонометрии. 2) Раскрыть методику работы с единичной окружностью (второй модели множества действительных чисел) в подготовительном курсе тригонометрии. 3) Показать роль единичной окружности и координатной прямой при обучении школьников решению тригонометрических уравнений, неравенств и их систем.
Учебно-тематический план
| № | Тема | Кол-во часов | Форма занятия |
| 1. | Подготовительный курс тригонометрии | 4 | 2 - лекция 2 - практическое занятие |
| 2. | Вычислительный аппарат тригонометрии. Тригонометрические тождества | 2 | лекция |
| 3. | Обратные тригонометрические функции | 4 | 2 - лекция 2 - практическое занятие |
| 4. | Приёмы решения тригонометрических уравнений, неравенств и их систем | 2 | лекция |
| 5. | Тригонометрические функции в материалах ЕГЭ по математике | 4 | 2 - лекция 2 - практическое занятие |
| | Итого | 16 часов | |
Содержание тем
1. Подготовительный курс тригонометрии.
Установление соответствия между множеством R (действительных чисел) и точками единичной окружности. Способы записи множеств чисел, соответствующих точкам единичной окружности. Основные типы упражнений подготовительного курса тригонометрии, выполняемые с помощью единичной окружности.
2. Вычислительный аппарат тригонометрии. Тригонометрические тождества.
Анализ вычислительного аппарата тригонометрии с целью выявления формул, в которых области определения выражений левой и правой частей не совпадают («опасные» формулы). Доказательство тригонометрических тождеств.
3. Обратные тригонометрические функции.
Определения arccina, arccosa, arctga, arcctgа, где а - некоторое число.
Функции
, 
, 
, 
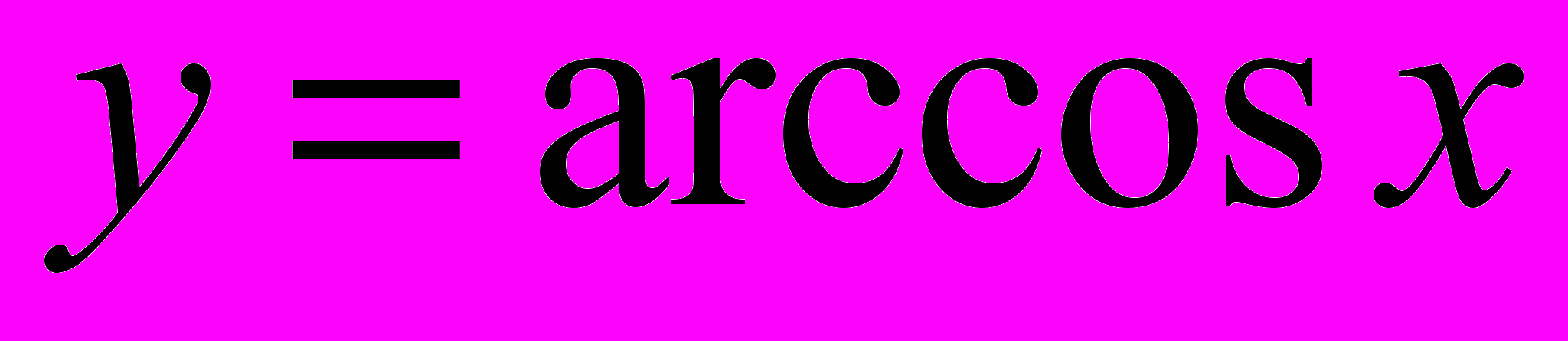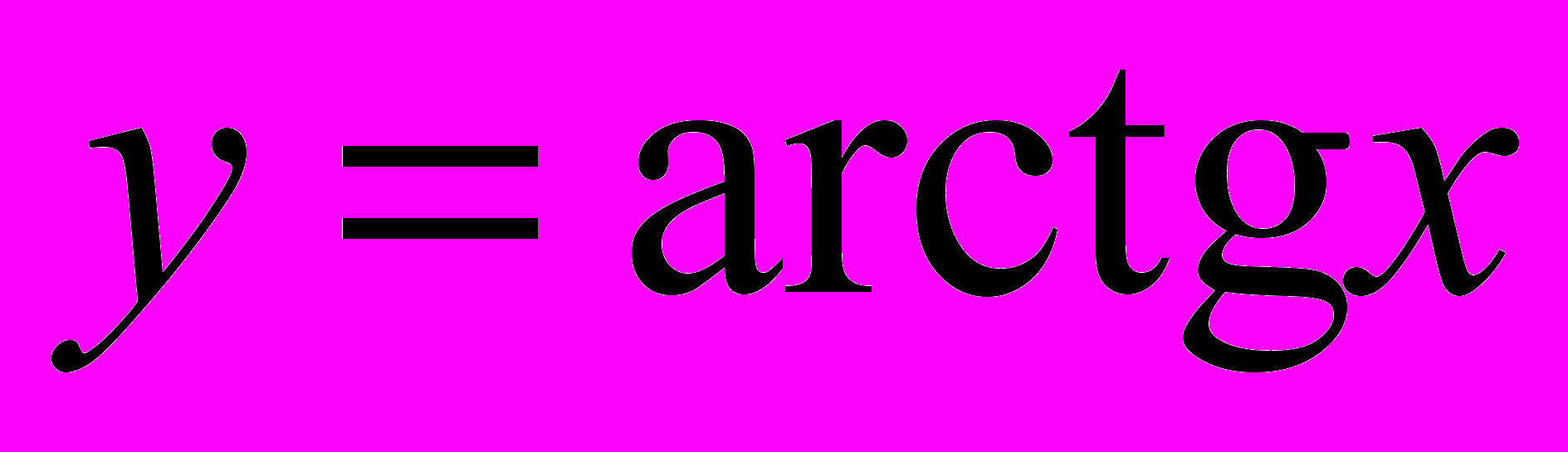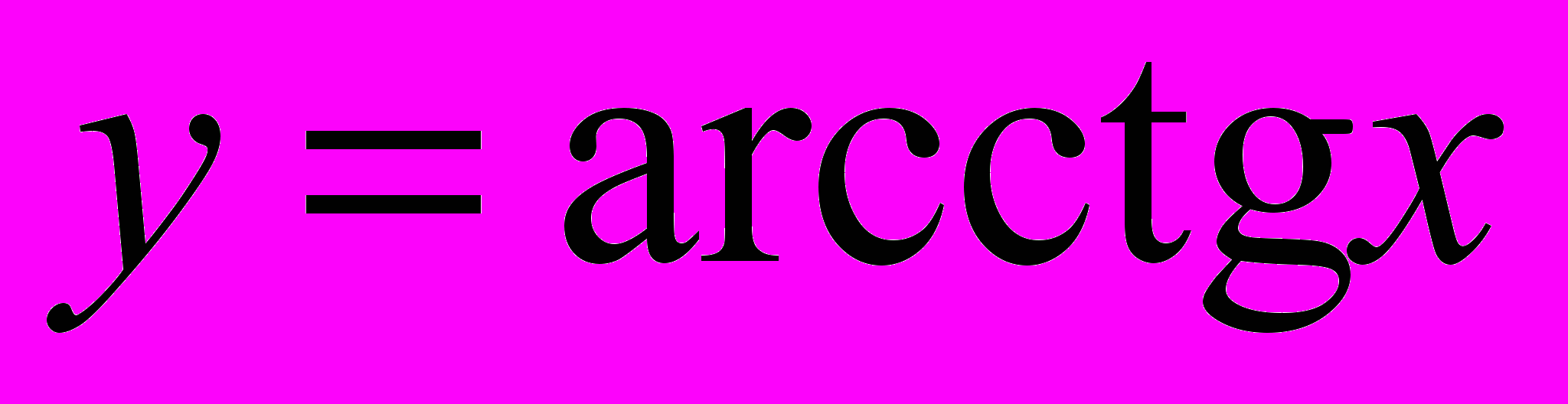(определения, графики, свойства). Нахождение значения прямой тригонометрической функции от значения обратной («правило прямоугольного треугольника»); нахождение значения обратной тригонометрической функции от значения прямой.Тождества, уравнения и неравенства с обратными тригонометрическими функциями.
4. Приёмы решения тригонометрических уравнений, неравенств и их систем.
Основные приёмы решения тригонометрических уравнений, уравнений и их систем. Использование единичной окружности и координатной прямой в процессе решения и записи ответа. Метод «лепестков». Простейшие тригонометрические уравнения и неравенства с параметром.
5. Тригонометрические функции в материалах ЕГЭ по математике.
Тождества, уравнения, неравенства и их системы с прямыми тригонометрическими функциями в заданиях ЕГЭ по математике. Обратные тригонометрические функции в упражнениях ЕГЭ.
Формы контроля:
- оформление теоретических карт:
1) единичная окружность; 2) пять способов записи чисел, соответствующих точкам единичной окружности; 3) анализ «опасных формул»; 4) графики обратных тригонометрических функций;
- «метод лепестков» при решении тригонометрических уравнений и неравенств (подбор и решения упражнений).
Модуль №9
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА В КУРСЕ АЛГЕБРЫ И НАЧАЛ АНАЛИЗА 10-11 КЛАССОВ
Цели. 1) Познакомить слушателей с методикой формирования основных понятий математического анализа на интуитивно-наглядном уровне через комплекс целесообразно подобранных задач. 2) Показать возможности лекционно-семинарской системы изложения материала в курсе алгебры и начал анализа в 10-11 классах. 3) Проанализировать возможности использования ЦОР в процессе изучения темы.
Учебно-тематический план
| № | Тема | Кол-во часов | Форма занятия |
| 1. | Методика формирования понятий: предел последовательности; предел в точке; непрерывность функции в точке; производная; первообразная. | 2 | лекция |
| 2. | Применение производной и первообразной | 2 | лекция |
| 3. | Лекционно-семинарская система изучения элементов математического анализа в общеобразовательных классах | 4 | 2 - лекция 2 - практическое занятие |
| 4. | Мастер-класс учителя высшей квалификационной категории (ВКК) МОУ СОШ №19 г.Воронежа Канатниковой В.И.: урок-конференция на тему «Приложения производной» | 2 | практическое занятие |
| 5. | Анализ электронного издания (ЭИ) «Математика 5-11. Практикум». -М.: Дрофа, 2004 | 4 | 2 - лекция 2 - практическое занятие |
| | Итого | 14 часов | |
Содержание тем
1. Методика формирования понятий: предел последовательности; предел в точке; непрерывность функции в точке; производная; первообразная.
Методика формирования понятия предела функции в точке на наглядно-интуитивном уровне через комплекс целесообразно разработанных задач. Конкретно-индуктивный метод введения понятий непрерывности функций в точке, производной, первообразной.
2. Применение производной и первообразной.
Методика изучения применения производной:
- касательная к графику функции;
- исследование функции и построение её графика;
- наибольшее и наименьшее значения функции на интервале;
- решение оптимизационных задач.
Методика изучения применения первообразной для вычисления площадей плоских фигур.
3. Лекционно-семинарская система изучения элементов математического анализа в общеобразовательных классах.
Особенности лекционно-семинарской системы изложения элементов математического анализа в курсе алгебры и начал анализа [2].
4. Мастер-класс учителя высшей квалификационной категории (ВКК) МОУ СОШ №19 г.Воронежа Канатниковой В.И.: урок-конференция на тему «Приложения производной».
Деловая игра [2].
5. Анализ электронного издания (ЭИ) «Математика 5-11. Практикум».
Анализ возможностей включения электронного издания «Математика 5-11. Практикум» в процессе изучения темы.
Формы контроля:
- теоретическая карта по теме «Предел функции в точке»;
- теоретическая карта с алгоритмами по теме «Применение производной»;
- участие в проведении и обсуждении мастер-класса учителя ВКК Канатниковой В.И. (МОУ СОШ №19 г.Воронежа) на тему «Урок-конференция».
Модуль №10
ИННОВАЦИОННЫЕ ТЕХНОЛОГИИ НА УРОКАХ МАТЕМАТИКИ
Цель. Формирование элементов профессиональной компетентности, обеспечивающей готовность слушателей к квалифицированному использованию инновационных технологий в процессе обучения школьников математике.