Geum.ru

Міністерство освіти І науки України Кіровоградський державний педагогічний університет імені Володимира Винниченка

Вид материалаДокументы

Содержание


30, тому що, добуток k
Подобный материал:
1   ...   8   9   10   11   12   13   14   15   ...   21

9 (7 балів). Довести, що ні при якому числа одночасно не можуть бути простими.

1. Очевидно, що при друге число , а тому не є простим, отже .

2. Якщо показник має непарні дільники виду , тобто , тоді перше число

– не є простим, тому не може мати непарних дільників.

3. Лишився один випадок, коли – парне натуральне число, що не має непарних дільників, тобто . Покажемо, що і за цих обставин три числа не можуть бути одночасно простими.

Пошуки ідеї та висунення робочої гіпотези: гіпотеза: . Доведення: база індукції (перевірена); індукційне припущення: має місце для . Покажемо істинність для , з урахуванням індукційного припущення маємо . А тоді третє число – ділиться на 3, а тому не є простим. Твердження доведено.


9 (4 бали). Для скількох пар цілих чисел справджується рівність .

Виразимо , а тоді , так як , то . Так як , то , де Аналогічно , , тоді , де

Тоді Очевидно, 14 пар цілих невід’ємних задовольняють останню умову.

Перевірка: при

і т.д.

Відповідь: 14 пар.


10 (4 бали). Для скількох пар цілих чисел справджується рівність .

Аналогічно: , і , ; і ,

Тоді

Відповідь: 9 пар.


11 (4 бали). Знайти усі трійки простих чисел , для яких справджується рівність .

Припустимо, що числа не діляться на три, тоді мають вигляд , а тоді мають вигляд ; ліва частина рівності не ділиться на три, а права частина при діленні на три дає остачу нуль: , тобто ділиться на три. Неможливо. Тому одне з чисел (наприклад, ) ділиться на три (і є простим), отже .

Маємо , , звідки . Нехай числа не діляться на три, аналогічно: мають вигляд ; тепер ліва частина рівності ділиться на три, а права частина при діленні на три дає остачу два: , тобто не ділиться на три. Неможливо. Тому одне з чисел (наприклад, ) ділиться на три, є простим, отже .

З рівності маємо , звідки .

Відповідь: 1 пара


10 (4 бали). Знайти всі пари простих натуральних чисел , для яких виконується умова .

Запишемо дану умову як квадратне рівняння відносно :

, знайдемо його корені

,

або

Аналіз першого розв’язку дозволяє зробити висновок, що при маємо пару простих , якщо просте і , - непарне, тоді - парне (не рівне двом), отже не може бути простим.

З другого розв’язку отримаємо (перебором) пари простих

Відповідь: ,


10 (4 бали). Довести: якщо ділиться на , то і ділиться на , де m, n, p, q – цілі числа.

За умовою, – ціле число. Розглянемо дріб та віднімемо від нього ціле число t:



Звідки ціле число.


9 (4 бали). Довести, що , де m – натуральне число.

Розв’язання:

.

Кожен доданок отриманої суми ділиться на 30, тому що, добуток k послідовних чисел натурального ряду ділиться на k! Перший доданок ділиться на 5!=120, другий – на 30, тому і сума ділиться на 30.


10 (2 бали). Знайти множину значень функції .

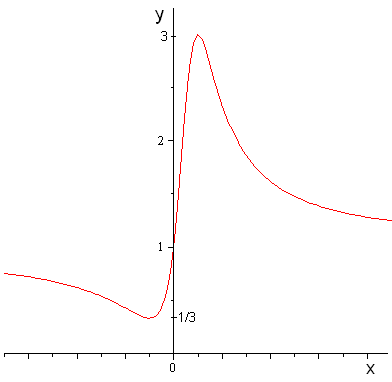. Обчисливши похідну, встановлюємо проміжки її знакосталості та критичні точки, маємо: на проміжку функція спадає: при ; ; на проміжку функція зростає: від до ; на проміжку функція спадає: ; при таким чином, маємо .

Відповідь: .


9 (7 балів). Побудувати графік функції .




М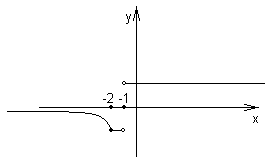аємо:




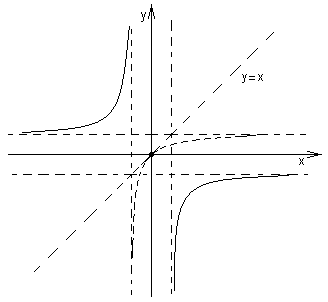
11 (4 бали). Побудувати графік функції .

ОДЗ: Знаменник не дорівнює нулю ні при яких значеннях аргументу.



У чисельнику: при неможливо; при виконується для усіх проміжку; при виконується для усіх . Тому ОДЗ: . Маємо:



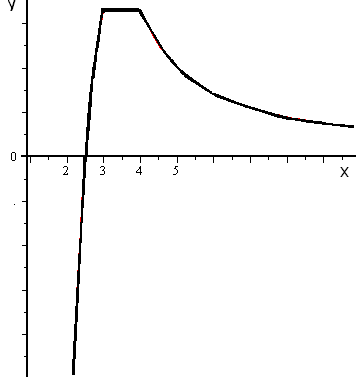
на першому проміжку – зростаюча функція (основа логарифма ): при ; на другому проміжку – стала функція (відрізок прямої); на третьому – спадна функція (частина гілки гіперболи): при .


9 (4 бали). Зобразити на площині множину точок , для координат яких справджується нерівність .

Ч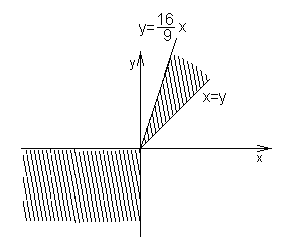исла і однакового знаку, тому нехай , тоді . Маємо першу чверть: .

Якщо , , ліва частина нерівності – недодатна, а права – невід’ємна, умова виконується для усіх точок третьої чверті і точки . Тому маємо множину точок:


9 (4 бали). На координатній площині зобразити множину точок , для яких .

Як легко переконатися, що разом з точкою , яка належить даній множині, дана множина містить точку . Тому побудуємо дану множину при умові і отриману фігуру відобразимо симетрично відносно прямої . При : , . Шукана множина є точка і 2 гілки, виділені суцільною лінією.