Geum.ru

Міністерство освіти І науки України Кіровоградський державний педагогічний університет імені Володимира Винниченка

Вид материалаДокументы
Подобный материал:
1   ...   4   5   6   7   8   9   10   11   ...   21

9 (4 бали). Довести, що .



=.


11 (4 бали). Побудувати графік функції

.

1 спосіб. ОДЗ: Перепишемо підкореневі вирази, врахувавши формулу куба суми та різниці:



. А тоді

для усіх

Г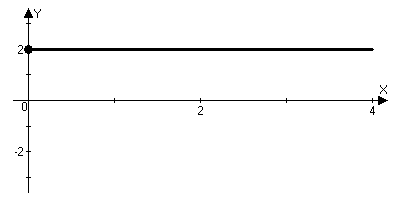рафіком функції є промінь з початком у точці , паралельний до вісі абсцис:

2 спосіб: знаходимо похідну функції, показуємо, що вона дорівнює нулю, а тому функція є сталою, обчислюємо , а тому


1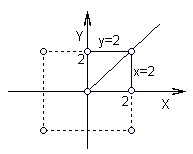1 (2 бали). На координатній площині Оху зобразити всі точки, для яких виконується рівність .

Рівняння допускає заміну на , отже, графік рівняння симетричний відносно вісі абсцис, допускає заміну на , тому графік симетричний відносно вісі ординат, допускає заміну на , отже, графік симетричний відносно початку координат, тому достатньо побудувати у першій чверті і відобразити симетрично відносно усіх осей і початку координат.

І чверть: якщо якщо .

Графік рівняння – квадрат з вершинами , .


10 (4 бали). На координатній площині Оху зобразити всі точки, для яких справджується рівність .

Перепишемо наше рівняння у рівносильному вигляді: , звідки

М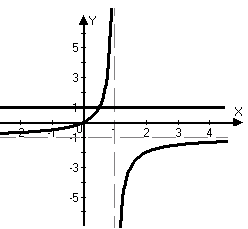аємо об’єднання двох графіків: пряму, паралельну вісі абсцис, і гіперболу з центром симетрії в точці (1; -1).


11 (4 бали). При яких значеннях параметра а графік матиме вісь симетрії?

Графіком функції є парабола, вітки якої напрямлені угору, тому вісь симетрії може бути тільки паралельна вісі ординат. Нехай - рівняння вісі симетрії. Тоді з того, що графіку належить точка з координатами випливає, що йому належить точка з тією ж ординатою.



Віднімемо почленно від першої рівності другу, матимемо:

або

Дана рівність має виконуватись для усіх значень невідомої , а це можливо лише при:



Останнє рівняння має раціональні корені:

, маємо

Отже, при значеннях параметра графік функції матиме вісь симетрії.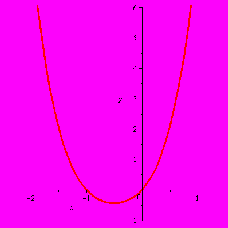





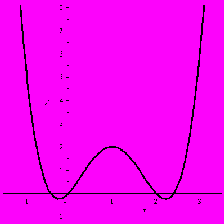
10 (4 бали). Знайти координати центра симетрії графіка .

Графіком функції є парабола, нехай - координати її центра симетрії. Тоді з того, що графіку належить точка з координатами , випливає, що йому належить точка . Отримаємо:



Додамо почленно до першої рівності другу, матимемо:

або





Відповідь: - координати центра симетрії графіка .

11 (2 бали). Знайти координати центра симетрії графіка .

Відповідь: - координати центра симетрії графіка .


1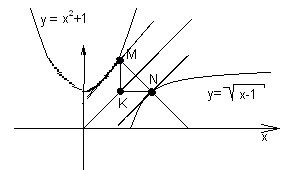1 (7 балів). Знайти найменшу відстань між точками та , які лежать відповідно на кривих і .

У 1 чверті графіки кривих і симетричні відносно прямої , тоді пряма перпендикулярна до , тобто якщо у точках і провести дотичні до графіків функцій, вони будуть паралельні прямій : ; ; ; (точки і симетричні відносно прямої ), тоді .


11 (4 бали). Розв’язати нерівність .

Розглянемо неперервну функцію , знайдемо , при якому , тоді . (*)

Піднесемо до кубу співвідношення (*) , спростимо вираз , замінимо суму, врахувавши (*), отримаємо: , , винесемо спільний множник за дужки, матимемо або , звідки , , . Перевіркою переконаємося, що не задовольняє (*), отже – сторонній корінь. Таким чином, для функції маємо єдиний корінь: . Розв’яжемо нерівність методом інтервалів, є два проміжки: та . Визначимо знак функції на кожному проміжку, обчислимо , тому ; , тому .

Якби для якогось , то тоді б за теоремою про проміжне значення неперервної функції існував би нуль функції на проміжку , а це не так, отже при . (Аналогічно і при ).

Тому розв’язок шуканої нерівності: .


10 (4 бали). Розв’язати рівняння .

Як легко видно,

.

Піднесемо обидві частини до квадрату і зробимо заміну , , , ; , . Так як , лишається лише , або , , . Оскільки (, а ), то врахувавши, що в даному випадку ми не могли отримати сторонніх коренів, приходимо до висновку, що корені: , .


10 (4 бали). Чи завжди із того, що числа і є раціональними, випливає, що обидва числа і є раціональними?

Нехай (при ), тоді , піднісши обидві частини до квадрату маємо: , - раціональне число. Аналогічно . Відповідь: так.


10 (2 бали). Нехай , , – натуральні числа. Чи може число бути простим натуральним числом?

Так. Міркуємо наступним чином: нехай, наприклад, , тоді число може бути простим, коли числа і – різної парності. Наприклад, при і : – просте; при і : ; при і : , або при і : і ін.


9 (4 бали). Нехай , – натуральні числа. Чи може число бути простим натуральним числом?

Розглянемо наш вираз як квадратний тричлен відносно невідомої та розкладемо його на множники:

;

.

А тоді отримаємо:

. Цей добуток може бути простим, якщо менший з множників дорівнює одиниці, а більший є простим числом. При перший множник менший за другий, а тому число може бути простим, тільки якщо , оцінимо, яким є другий множник: і є непростим для усіх . Очевидно, якщо - перший множний не дорівнює одиниці, другий за нього – більший, а тому число є складеним.

Відповідь: число не може бути простим.