Міністерство освіти І науки України Кіровоградський державний педагогічний університет імені Володимира Винниченка
| Вид материала | Документы |
- Міністерство освіти І науки україни «Переяслав – Хмельницький державний педагогічний, 554.03kb.
- Міністерство освіти І науки україни двнз«Переяслав – Хмельницький державний педагогічний, 1277.11kb.
- Міністерство освіти І науки, молоді та спорту україни уманський національний університет, 29.37kb.
- Міністерство освіти І науки україни полтавський державний педагогічний університет, 680.62kb.
- Міністерство освіти І науки україни переяслав-хмельницький державний педагогічний університет, 616.99kb.
- Міністерство освіти І науки України, 1659.87kb.
- Міністерство освіти І науки україни мелітопольський державний педагогічний університет, 2525.18kb.
- Південноукраїнський державний педагогічний університет імені К. Д. Ушинського (м. Одеса), 349.4kb.
- Міністерство освіти І науки, молоді та спорту україни уманський національний університет, 30.09kb.
- Міністерство освіти І науки України Слов’янський державний педагогічний університет, 2976.14kb.
10 (4 бали). Знайти найменший цілий корінь рівняння
 , що має два різні корені.
, що має два різні корені.З умови задачі:

 ; найменше значення маємо при
; найменше значення маємо при  ;
;  ;
;  .
.Перевірка:

 ,
, 
 .
. Якщо
 - спадає,
- спадає,  - зростає,
- зростає,  при
при  .
.Відповідь: при
 ;
;  ;
;  .
.11 (2 бали). Знайти найбільше значення функції
 , якщо
, якщо  набуває тільки натуральних значень.
набуває тільки натуральних значень.Обчисливши похідну

 , отримаємо єдину точку
, отримаємо єдину точку  , в якій похідна рівна нулю:
, в якій похідна рівна нулю:  , причому якщо
, причому якщо  і
і  , а тому в точці
, а тому в точці  функція досягає максимуму. Оскільки
функція досягає максимуму. Оскільки  , обчислюємо
, обчислюємо  і
і  та переконуємося, що
та переконуємося, що  . Зауваження: функція (і похідна) визначені для усіх
. Зауваження: функція (і похідна) визначені для усіх  .
. Відповідь: при
 ;
;  .
.10 (7 балів). Розв’язати нерівність
 .
.


Відповідь:

11 (4 бали). Знайти значення
 , при якому сума квадратів коренів рівняння
, при якому сума квадратів коренів рівняння  найменша.
найменша.Нехай
 ,
,  – корені рівняння. Враховуючи теорему Вієта
– корені рівняння. Враховуючи теорему Вієта  , отримаємо:
, отримаємо:  . Найменше значення вираз набуває при
. Найменше значення вираз набуває при  .
. Зауваження: додатковою перевіркою встановлюємо: при
 дискримінант
дискримінант  , тобто корені рівняння – дійсні числа. Якщо виявиться, що при даному значенні
, тобто корені рівняння – дійсні числа. Якщо виявиться, що при даному значенні 
 , то розв’язання задачі рівносильне відшуканню найменшого значення виразу за обмежень
, то розв’язання задачі рівносильне відшуканню найменшого значення виразу за обмежень  , наприклад: якщо задача звучить так: Знайти значення
, наприклад: якщо задача звучить так: Знайти значення  , при якому сума квадратів коренів рівняння
, при якому сума квадратів коренів рівняння  найменша. При розв’язанні приходимо до
найменша. При розв’язанні приходимо до  , а тоді:
, а тоді:

Звідки
 . Побудувавши параболу
. Побудувавши параболу  в системі координат
в системі координат  і відмітивши допустимі значення
і відмітивши допустимі значення  , отримаємо, що при
, отримаємо, що при  сума
сума  є найменшою. Причому ми розв’язуємо рівняння в множині дійсних чисел.
є найменшою. Причому ми розв’язуємо рівняння в множині дійсних чисел.10 (4 бали). При яких значеннях параметра
 кожне з рівнянь
кожне з рівнянь  та
та  має по два цілих кореня?
має по два цілих кореня?Умови існування коренів:


 Звідки
Звідки  . Очевидно, що при
. Очевидно, що при  , число
, число  є непарним. Умова цілочисельності вимагає
є непарним. Умова цілочисельності вимагає  таких щоб
таких щоб 
 або
або  - прийшли до діофантового рівняння. Оскільки
- прийшли до діофантового рівняння. Оскільки  другий співмножник додатний, тому і перший повинен бути додатним, крім того, перший множник не перевищує другого, тому лишається єдина можливість:
другий співмножник додатний, тому і перший повинен бути додатним, крім того, перший множник не перевищує другого, тому лишається єдина можливість:


 .
.10 (7 балів). Для всіх дійсних значень параметра
 розв’язати рівняння
розв’язати рівняння  .
.ОДЗ:


 ,
,


При
 корені, обчислені за обома формулами,
корені, обчислені за обома формулами,  співпадають. При
співпадають. При  корені
корені  теж співпадають.
теж співпадають. Відповідь: якщо
 якщо
якщо  .
.11 (7 балів). Яким має бути число
 , щоб існувало рівно чотири різні пари чисел
, щоб існувало рівно чотири різні пари чисел  , для яких справджуються обидві рівності
, для яких справджуються обидві рівності  .
.1 спосіб. Вказівка до розв’язання:
Перепишемо

 - є рівняння точки чи еліпса (кола, стиснутого в 5 разів до вісі Оу) при
- є рівняння точки чи еліпса (кола, стиснутого в 5 разів до вісі Оу) при  , для якого центром симетрії є точка
, для якого центром симетрії є точка  . При
. При  рівняння не задовольняє жодна дійсна точка. Тому
рівняння не задовольняє жодна дійсна точка. Тому  . Для
. Для  маємо рівняння кривої
маємо рівняння кривої  , для
, для  маємо рівняння кривої
маємо рівняння кривої  . Для другої кривої
. Для другої кривої  центром симетрії є точка
центром симетрії є точка  . При
. При  рівняння рівносильне до
рівняння рівносильне до  чи
чи  . Тому достатньо знайти такі значення параметра, при яких є рівно одна спільна точка у обох функцій (в області
. Тому достатньо знайти такі значення параметра, при яких є рівно одна спільна точка у обох функцій (в області  ).
). Обчисливши похідні двох функцій і прирівнявши їх та значення обох функцій в точці дотику, маємо значення для параметра
 , точка дотику
, точка дотику  , інші точки – симетричні відносно прямої
, інші точки – симетричні відносно прямої  .
. Друге граничне значення параметра отримаємо у точці, де похідна не існує,
 , чотири спільні точки показано на рисунку.
, чотири спільні точки показано на рисунку.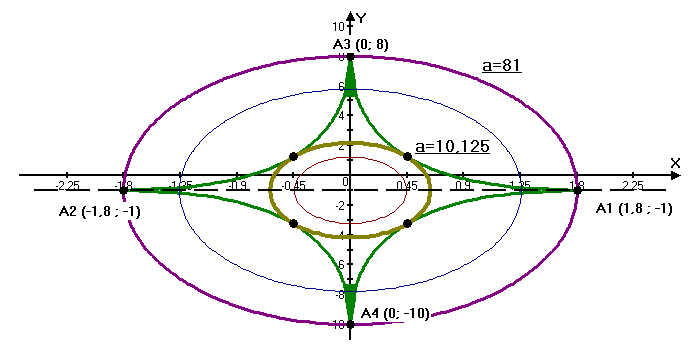
2 спосіб: Якщо проаналізувати 1 спосіб, то видно, що ми йшли по стандартній схемі: спільна точка - спільна дотична - похідні в точці рівні і т.д. Насправді усі обчислення є досить громіздкими і тому виникло природне бажання знайти інше розв’язання.
З умови
 при виконанні заміни
при виконанні заміни  , що відповідає паралельному перенесенню початку координат в точку (0;-1) і розтягу вздовж осі абсцис у 5 разів (від осі
, що відповідає паралельному перенесенню початку координат в точку (0;-1) і розтягу вздовж осі абсцис у 5 разів (від осі  ), маємо
), маємо  симетричну систему рівнянь відносно невідомих
симетричну систему рівнянь відносно невідомих  . Аналіз дозволяє зробити висновки, що як тільки пара (точка) з координатами
. Аналіз дозволяє зробити висновки, що як тільки пара (точка) з координатами  задовольняє умови системи, то і точки з координатами
задовольняє умови системи, то і точки з координатами  - задовольняють теж. Оскільки умова вимагає наявність лише чотирьох точок, то:
- задовольняють теж. Оскільки умова вимагає наявність лише чотирьох точок, то:а) або точки
 співпадають, тобто
співпадають, тобто  , або
, або б)
 або
або  , тобто
, тобто  або
або  .
.Розв’язання системи у випадку а):

 і точки
і точки  ; у випадку б)
; у випадку б)  або
або  , а тоді
, а тоді  - отримуємо 4 точки
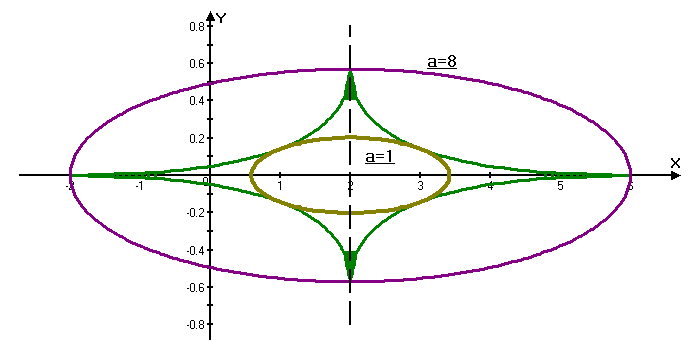
- отримуємо 4 точки  , зображені на рисунку.
, зображені на рисунку.Відповідь:
 або
або  .
.11 (7 балів). Знайти всі числа
 , для яких існує чотири такі різні пари чисел
, для яких існує чотири такі різні пари чисел  , що справджуються обидві рівності
, що справджуються обидві рівності  і
і  .
.Дивись другий спосіб розв’язання попередньої задачі: заміна
 , що відповідає паралельному перенесенню початку координат в точку (2; 0) і розтягу вздовж осі ординат, приводить до
, що відповідає паралельному перенесенню початку координат в точку (2; 0) і розтягу вздовж осі ординат, приводить до  симетричної системи рівнянь відносно невідомих
симетричної системи рівнянь відносно невідомих  .
.  або
або  .
.Відповідь:
 або
або  .
.
11 (2 бали). Спростити вираз
 .
.Аналізуючи ОДЗ, помічаємо, що
 приймають значень однакового знаку. Якщо
приймають значень однакового знаку. Якщо  Якщо
Якщо 
11 (2 бали). Обчислити
 .
.


10 (4 бали). Довести, що
 .
.

 =
= .
.10 (4 бали). Довести, що
 .
.

 =
= .
.