Geum.ru

Міністерство освіти І науки України Кіровоградський державний педагогічний університет імені Володимира Винниченка

Вид материалаДокументы
Подобный материал:
1   2   3   4   5   6   7   8   9   ...   21

10 (4 бали). Довести нерівність .

2 спосіб. Нехай , тоді розглянемо функцію при умові (враховано, що і ). Функція Лагранжа .

, , при . Звідси і з умови маємо пари : , . Легко показати (перевірте!), що і .

Розглянемо випадки і . При маємо: , звідси

, тому

.

При , , аналогічно, . і є коренями рівняння (за Вієтом) . Тепер потрібно знайти і і відповідне значення та перевірити, що воно менше 25. На межі маємо пари : , , , з відповідними значеннями : -24, 24, 24, -24. Отже, . Нерівність доведено.


11 (7 балів). Якщо - внутрішні кути трикутника, , то . Довести це твердження.

Враховуючи відомі формули тригонометрії, маємо:




10 (7 балів). Нехай - внутрішні кути трикутника і справджується рівність . Довести, що максимум значень кутів можливий тільки для рівностороннього трикутника.

1 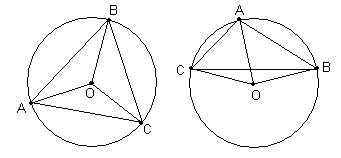спосіб. Розглянемо з кутами відповідно. Нехай - його радіуси описаного і вписаного кіл, - його площа, - півпериметр, - центри описаного і вписаного кіл. Якщо - гострокутний, то , або , якщо - негострокутний (наприклад, – тупий), то . Як відомо (наприклад, з відомої класичної формули Ейлера ), (нерівність Ейлера), тому (тут враховано теорему синусів: ), звідки . Рівність можлива лише коли , тобто - рівносторонній (, звідки , ).

2 спосіб. Розглянемо функцію

на компакті . Функція Лагранжа: . , звідки Розглянемо рівняння . , , . Зазначимо, що якщо (), то . Тому два з кутів рівні. Нехай , тоді , ,



причому рівність можлива, лише коли , або , . На межі: 1) , , , причому рівність можлива лише коли . 2) , звідси , . Отже, максимальне значення функції : 0 і досягається для наступних трійок , , , . У випадку кутів трикутника нам прийнятний лише перший варіант.


11 (2 бали). Розв’язати рівняння .

ОДЗ: ; ;

; ; .


11 (4 бали). Розв’язати нерівність .

ОДЗ:

Введемо заміну: ; . ;


11 (7 балів). Розв’язати рівняння .

Введемо заміну , тоді , звідки і , а тоді ; ; , маємо кубічне рівняння відносно з цілими коефіцієнтами , корені шукаємо за схемою Горнера серед дільників вільного члена:



– сторонні корені, маємо: , а тоді , повернемося до заміни: , або . Отримані значення входять в ОДЗ:

Відповідь: .


11 (4 бали). Знайти всі , для яких справджуються обидві рівності: та

ОДЗ: . Розглянемо першу умову: . Введемо заміну , маємо , звідки . Повертаючись до заміни та враховуючи другу умову, маємо (з урахуванням ОДЗ):




11 (7 балів). Розв’язати рівняння .

1 спосіб.

, а тоді

, звідки , , а тоді , , , , тому , , . Як легко переконатися, повинно бути парним, тому , .

2 спосіб. ОДЗ: перейдемо до нової основи, наприклад, , отримаємо: , позначимо , врахуємо, що логарифм добутку дорівнює сумі логарифмів, маємо: , звідки розв’язуємо квадратне рівняння , отримуємо . Враховуючи заміну і ОДЗ (І чверть), маємо , .


11 (7 балів). Розв’язати рівняння

.

ОДЗ: перші дві умови дають обмеження .

Якщо усі 4 умови виконуються, вихідне рівняння приводить до:

Перше рівняння не задовольняє четверту умову ОДЗ, тому , звідки . Оскільки то з розв’язку у цей проміжок попадають , а з розв’язку у цей проміжок попадають , перевіряємо, які з розв’язків задовольняють дві останні умови ОДЗ:

для - друга умова не виконується;

- друга умова не виконується;

- друга умова не виконується;

умови виконуються.

Відповідь: