Geum.ru

Міністерство освіти І науки України Кіровоградський державний педагогічний університет імені Володимира Винниченка

Вид материалаДокументы

Содержание


Розв’язати рівняння
Подобный материал:
1   2   3   4   5   6   7   8   9   ...   21

11 (7 балів). Розв’язати рівняння

.

ОДЗ:

Враховуючи множину значень функції косинус і те, що права частина 1, маємо дві можливості:





Друга рівність рівносильна до що неможливо за натуральних значень . З умови Нескладно перевіряється неможливість виконання умови при від’ємному значенні невідомої , наприклад, помноживши на () ліву і праву частини, та при .

З першої рівності маємо . Тому . Далі перепишемо у вигляді . При рівність неможлива, бо ліва частина більша від 4, при отримаємо , а тоді (входить в ОДЗ). Якщо , домножимо ліву і праву частини на , при цьому ліва частина не буде ділитися на 4, а права – буде. Що неможливо. Тому маємо єдину можливість.

Відповідь: .


11 (7 балів). Розв’язати нерівність .

Дослідимо графіки функцій та .

1. ,

ОДЗ: ,

координати вершини: ; графік симетричний відносно прямої ; точки перетину з віссю абсцис ; точка перетину з віссю ординат ; за рахунок симетрії відносно прямої , графік функції проходить через точку ; ; . На проміжку функція є спадною; на проміжку функція є зростаючою.

2. , графік симетричний відносно прямої . Найменше значення , точка перетину з віссю ординат ; за рахунок симетрії відносно прямої , графік проходить через точку .

При маємо , функція є зростаючою, на проміжку функція є спадною.

Аналіз дозволяє зробити наступні висновки:

н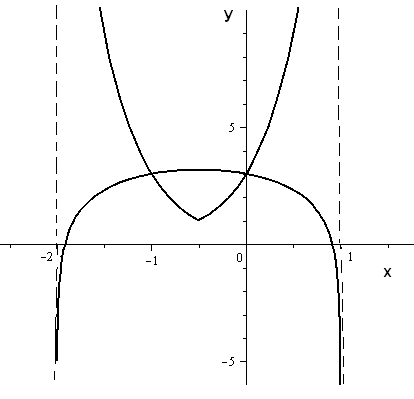а проміжку одна з функцій є зростаючою, а інша – спадною, тому вони можуть мати не більше однієї точки перетину, ця точка – ;

на проміжку одна функція є спадною, а інша – зростаючою, тому міркуючи аналогічно, на цьому проміжку маємо точку – . Таким чином, Для нерівності маємо .

Відповідь: .


11 (7 балів). Розв’язати рівняння .

ОДЗ: . Враховуючи, що та , маємо: , .

Нехай , тоді , , . Маємо

, , , .


11 (4 бали). Розв’язати нерівність .

Розв’язання:

.



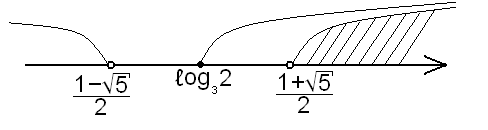
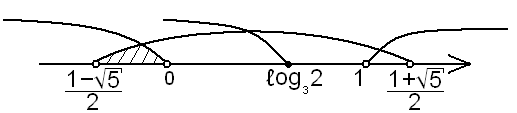
, , . Розглянувши перетини відповідних множин отримаємо розв’язок: .


11 (4 бали). Розв’язати рівняння .

Очевидно, розв’язком рівняння є Покажемо, що інших розв’язків немає: у лівій частині рівняння – зростаюча функція, у правій – спадна (на всій області визначення ), тому графіки цих функцій можуть мати одну точку перетину, а отже рівняння має єдиний корінь.


11 (4 бали). Розв’язати рівняння .

Очевидно, розв’язком рівняння є Перепишемо рівняння у рівносильному вигляді: . У лівій частині – спадна функція, у правій – зростаюча (на всій числовій прямій), тому рівняння має єдиний корінь:


11 (7 балів). Розв’язати рівняння

Введемо позначення: , обчислимо похідну , критичні точки . Для оцінки цього числа міркуємо наступним чином:



а тоді для похідна , функція зростає, причому на кінцях проміжку функція приймає значень протилежних знаків, наприклад , а тому на проміжку є рівно один корінь. Так як , то цей корінь локалізовано , нескладно побачити, що

На проміжку похідна , функція спадає, причому на кінцях проміжку функція приймає значень протилежних знаків, це випливає, наприклад, з того, що , , а тому на проміжку є рівно один корінь, цей корінь

Відповідь:


11 (2 бали). Скільки коренів має рівняння ? Вказати один з коренів.

. є коренем.

1) – зростаюча,

2) – зростаюча ,

3) – сума зростаючих функцій – зростаюча функція.

4) Корінь єдиний .


11 (2 бали). Знайти рівняння дотичної до графіка при .

; ; ; .

1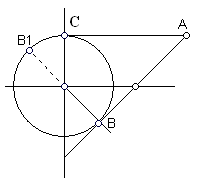1 (4 бали). Знайти рівняння дотичних до кола , що проходять через точку .

1 спосіб. Одна з дотичних , її рівняння: . Довжина дотичної АС дорівнює 5, отже, довжина другої дотичної теж 5.

Нехай  ;

; ; ; ,

, , , ,

.

; рівняння прямої за точкою і нормальним вектором або .

Відповідь: .

2 спосіб. Рівняння дотичної ; , похідна ; тоді . Маємо – рівняння дотичної; оскільки вона проходить через точку , то:

; ;

, , ,

а тоді маємо 2 рівняння дотичних:

1) , звідки ;

2) або

або .

Відповідь: .


11 (4 бали). Знайти точку на кривій , найближчу до прямої .

Знайдемо дотичні до кривої, паралельні до даної прямої, тоді їхні кутові коефіцієнти .



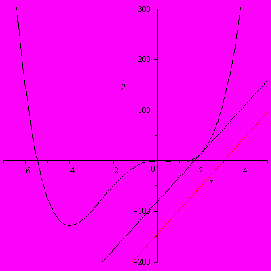
Маємо точки , ; , ; , ; та рівняння дотичних, відповідно: першої , ; другої , ; третьої , . Аналіз рівнянь чотирьох прямих: даної прямої , дотичних , , дозволяє зробити висновок: найближче знаходиться дотична , найдалі – дотична . Тому найближче до прямої знаходиться точка кривої (2;16).

Зауваження: Можна було скористатися формулою відстані від точки до прямої

.

10 (4 бали). Розв’язати систему рівнянь

Система є симетричною відносно двох невідомих, тому можна виразити усе через симетричні многочлени від двох невідомих і , а оскільки можна отримати рівняння відносно :



виділимо :









;

; виконаємо заміну ; матимемо , . Отримуємо:

Розв’яжемо рівняння:



.