Концепция профильного обучения 57 Базисный учебный план профильного обучения 62

Вид материала

Реферат

Содержание

Подобный материал:

1 ... 10 11 12 13 14 15 16 17 18

Тема 10 Дистанционная поддержка обучения естествознанию

Ссылки на файлы:

КДО, Полат, ХуторскойВирт, Шарапков

План занятия

Дистанционная поддержка обучения физическим законам

Дистанционная поддержка изучения вопросов биологии

Дистанционная поддержка изучения географических вопросов

Дистанционная поддержка химических знаний

Ваша работа может считаться успешной, если в конце занятия Вы

Информационный блок

Обучение Естествознанию в профильной школе предполагает самостоятельную работу учащихся, которая может быть организована с применением программно– педагогических средств и средств сети Интернет.

Примеры организации и реализации дистанционной поддержки профильного обучения разработаны применительно к сформированному и описанному аннотированному каталогу, размещенному на сайте Российского общеобразовательного портала по адресу (ссылка скрыта).

Отсутствие учебников по Естествознанию создает определенные проблемы для качественного преподавания его в школе, однако в сети Интернет есть сайты, посвященные концепциям современного естествознания. С определенной долей профанации эти электронные ресурсы могут быть рекомендованы для учащихся. Ознакомиться с дистанционными учебниками по естествознанию можно по адресам:

ссылка скрыта

ссылка скрыта

ссылка скрыта

ссылка скрыта

ссылка скрыта

Поскольку на начальном этапе преподавание естествознания в школе будет осуществляться учителями–предметниками, для повышения эффективности обучения целесообразно использовать электронные ресурсы.

Рубрика Мнение (ссылка на файлы Полат, ХуторскойВирт, Шарапков)

Методические рекомендации по их использованию рассмотрим далее.

Дистанционная поддержка обучения физическим законам

Характеристика Интернет-ресурсов для дистанционной поддержки обучения физике:

Электронные учебники. Программно-методический комплекс, обеспечивающий возможность самостоятельно освоить учебный курс или его раздел. Объединяет в себе: учебник, справочник, задачник и лабораторный практикум (контент), информационно-коммуникативные средства.

Предметно-ориентированные среды. Учебный пакет программ. Компьютерные системы математического моделирования реальных физических явлений.

Лабораторные практикумы. Программы служат для проведения наблюдений за объектами, за их взаимосвязями или их свойствами. Должны содержать аппарат обработки результатов, их наглядного представления.

Тренажеры. Программы служат для отработки и закрепления определенных навыков. Должны содержать теоретический и справочный материал, возможность тренировки на различных уровнях самостоятельности, контроль и самоконтроль.

Контролирующие программы. Предназначены для проверки и оценки качества знаний. Должны быть обеспечены фиксация результатов контроля, их сбор, распечатка и статистический анализ.

Справочники. Они предназначены для хранения учебной информации. Программы характеризуются иерархической организацией материала и возможностью быстрого поиска информации по различным основаниям.

Частно-дидактические методы обучения физике с использованием Интернет-ресурсов:

Метод целесообразно подобранных задач (метод циклов). «Обучение через задачи» - один из методов проблемного обучения, реализуемый на основе системы задач, объединенных между собой одной общей идеей исследования (проблемой), ориентированной на получение новых теоретических знаний.

В современной методике решения физических задач, ориентированных на развитие умений математического и компьютерного моделирования можно выделить несколько циклов задач:

– Задачи, ориентированные на развитие умений моделирования физических явлений.

– Задачи, иллюстрирующие иерархический подход в математическом моделировании.

– Задачи, ориентированные на развитие умений построения физических моделей сложных явлений и трудно формализуемых объектов.

– Задачи, ориентированные на установление границ применимости используемых физических моделей.

– Задачи, ориентированные на изучение свойств математической модели.

– Задачи, ориентированные на последовательное использование строго определенных физических понятий и величин.

– Компьютерные задачи по физике, связанные с проведением учебного вычислительного эксперимента для достижения конкретной дидактической цели.

– Компьютерные задачи межпредметного характера с применением компьютерной графики, численного анализа, статистических методов (интегративный цикл задач).

Принципы составления циклов задач в профильном обучении на основе Интернет-ресурсов:

– Необходимо учитывать общую ориентацию школы и специфику контингента учащихся конкретного профильного класса.

– Задачи цикла должны быть связаны между собой не однозначной линейной логической связью, а допускать возможность различной последовательности рассмотрения предлагаемых задач, позволяя тем самым, достичь необходимого уровня понимания изучаемого вопроса не единственным образом.

– Возможность для продолжения и развития анализа ситуаций, выходящие за рамки традиционного школьного курса физики, переходя, таким образом, на следующий уровень физического понимания путем изменения проблемы и спектра вопросов, переосмысления имеющихся знаний и их реструктуризация.

– Индивидуализация обучения на основе доступности задач для наиболее способных учащихся, которые являются выразителями творческого потенциала своего поколения.

– Сочетание задач, относящихся к различным разделам физики, но предоставляющие возможность обратить особое внимание на какой- то определенный компонент действий в цикле математического моделирования.

– В условии задачи особое внимание обращается не на исчерпывающую постановку вопроса, а на поиск круга вопросов, на которые можно найти ответы в рамках рассматриваемой модели изучаемого явления.

– Установление области справедливости ответа (границ применимости модели) еще до получения его в явном виде.

– Применения физических законов разных методологических уровней.

– Направленность на творчество, характеризующая стремление к нестандартным действиям, критичность мышления, отражающая способность к анализу, синтезу, рефлексии и чувство новизны как психоэмоциональное состояние обучаемого, стимулирующее поисковую эвристическую деятельность.

Метод демонстрационных примеров. Компьютерное моделирование является наиболее адекватным современным требованиям к системе образования методом включения компьютера в обучение, обеспечивающим активный вид учебной деятельности. Преимущества учебного компьютерного моделирования связаны с преодолением формальности усвоения знаний, развитием исследовательских и конструкторских навыков, развитием интеллектуальных способностей учащихся. Использование компьютерного моделирования в учебном процессе (исследование явлений на основе готовых моделей (simulation), построение моделей самими учащимися (modelling) позволяет повысить интенсивность обучения в рамках деятельностного подхода. В учебном компьютерном моделировании учебные информационные модели являются демонстрационными примерами, а метод обучения с их использованием – методом демонстрационных примеров. Демонстрационные примеры включают исходные тексты программ на языках программирования. Поэтому часто компьютерные средства обучения для поддержки метода демонстрационных примеров минимальны: необходимы лишь текстовый процессор (желательно с поддержкой гипертекста) и система программирования на выбранном языке (например, BASIC, Pascal, С или MAPLE). Впервые данный метод предложен В.В. Лаптевым и М.В. Швецким, и описан в монографии «Методическая система фундаментальной подготовки в области информатики: теория и практика многоуровневого педагогического университетского образования» (СПб: Изд-во СПбГУ, 2000. – 508 с.). Развитие данного метола было предложено И.И. Рыжовой в монографии «Методическая теория обучения информатике аспекты фундаментальной подготовки» (В.В. Лаптев, Н.И. Рыжова, М.В. Швецкий. СПб: Изд-во СПбГУ, 2003. – 352 с).

Метод учебно-игрового моделирования (компьютерные игры). Компьютерные алгоритмические игры физического содержания, основанные на информационном, математическом моделировании, как и другие дидактические игры, должны способствовать решению учебной задачи урока, например закреплению знаний, лучшему усвоению методов решения задач, развитию алгоритмической культуры. С помощью компьютерных игр становится достижимой интенсификация обучения, за счет чередования информационного и практического обучения с включением эмоциональных моментов. Такое сочетание является удачным способом повысить эмоциональную привлекательность и удовлетворенность учебной деятельностью. В игре могут принимать участие от одного до нескольких игроков Соревнование (особенно в группе) в полной мере усиливает познавагельный интерес.

Метод учебных моделей научного исследования. Сложный, комплексный характер современных научных исследований в сочетании с ограниченным временем, отпускаемым на их решение, требует качественного скачка в подготовке специалистов, способных справиться с решением подобного рода задач. Это, в первую очередь, означает необходимость раннего выявления лиц, обладающих соответствующими способностями, и развития навыков к исследовательской деятельности на раннем этапе развития личности. С развитием новых информационных технологий обучения можно говорить об определенных универсальных исследовательских умениях и навыках, связанных с возможностью реализации цикла научного творчества, независимо от конкретного объекта исследования. Развитие исследовательской компетенции учащихся рассматривается применительно к проведению комплексных теоретико-экспериментальных исследований по разработке физических и математических моделей явлений природы с последующим проведением вычислительного эксперимента.

Метод проектов. Применение метода проектов способствует зарождению новых отношений знания-умения, необходимых для жизни. Логика проектов не подчинена ни логике преподавания предмета, ни требованиям экзаменов, она более гибкая и прагматичная. Проектная технология имеет особую ценность, так как закладывает основы проектной культуры учащихся. Проектная культура субъекта имеет двойственную природу. Это и совокупность взглядов и представлений об искусственном мире, другими словами, картина искусственного мира и, одновременно, это обобщенный личностный механизм, который используется для «изобретения» этого мира. Опыт приобретения способов деятельности и опыт творчества, приобретаемый при работе над проектами. Содержание включает в себя не только опыт практического применения методологических, предметных, межпредметных или над-предметных знаний, а опыт коллективной деятельности, опыт процедурного мышления.

Метод натурно-вычислительного эксперимента. Интеграция физического эксперимента основывается на определенной аналогии между вычислительным и натурным экспериментами. На компьютере (экспериментальной установке) проводятся вычисления (измерения), которые в дальнейшем анализируются для постановки новых экспериментов. Изучая на ЭВМ поведение модели, исследователь как бы испытывает саму природу (конструкцию, процесс), задавая ей вопросы и получая достаточно полные достоверные ответы. Учебный натурно-вычислительный эксперимент, как научный метод обучения, включает как репродуктивную, так и творческую деятельность школьников, т.к. без воспроизведения определенных знаний о моделировании, программировании (репродуктивная деятельность учащихся) затруднительно написать даже самую простую программу (творческая деятельность учащихся).

Формы организации учебных занятий

Лабораторный компьютерный физический практикум Целью лабораторных работ на основе метода демонстрационных примеров и натурно-вычислительного эксперимента является закрепление и углубление теоретических знаний, приобретение школьниками практических навыков в области методологии вычислительной физики.

Методические рекомендации для лабораторных работ включают:

1) гипертекстовый документ, содержащий:

– формулировку темы, основную цель, требования к подготовке школьников, планируемые результаты обучения;

– краткое изложение теории (понятий, моделей и алгоритмов), необходимой для выполнения заданий;

2) демонстрационные примеры. При составлении и подборе демонстрационных примеров программы представляются в их окончательном виде на том языке, на котором они могут реально выполняться на компьютере;

3) задания для самостоятельного выполнения.

Межпредметные деловые игры. Методика развития универсальных умений и навыков исследовательской деятельности в рамках рационально-научного подхода основывается на рассмотрении комплексных задач методами математического моделирования и вычислительного эксперимента.

Деловая игра, позволяющая разрабатывать гибкие стратегии решения сложной проблемы. Каждый участник игры может выступать в различных ролях, выявляя свои интересы и склонности.

Форма занятий проблемного обучения должна учитывать комплексный характер выбранной научной проблемы, поэтому одним из наиболее целесообразных способов реализации учебной модели научного исследования является организация длительной межпредметной деловой игры, проводимой учителем физики при участии преподавателей других учебных дисциплин. Комплексный характер научной проблемы представляет собой главное отличие предлагаемого подхода к развитию навыков исследовательской деятельности по сравнению с традиционными методами развития творческих способностей на основе решения учебных задач в определенной области знания.

Деловая игра позволяет наилучшим образом реализовать принцип учебной модели научного исследования в рамках дидактики межпредметной интеграции позволяющей максимально индивидуализировать учебный процесс. При этом одним из главных достоинств является радикальное сокращение времени накопления опыта.

Технология деловой игры – это конкретная методика проблемного обучения: игровая проблемная ситуация возникает как бы произвольно, она предопределена правилами самой игры, что, в свою очередь, способствует возникновению новых проблем. Это помогает возникновению положительного эмоционального настроя, заинтересованности в разрешении проблемы и формирования не только творческих умений, но и определенных черт личности. Ведущими способами деятельности при этом должны стать сложные интеллектуальные операции, соответствующие научно-значимым умениям исследовательской деятельности.

Семинары по решению задач на компьютере. Учебный вычислительный эксперимент (термин впервые введен Н.И. Рыжовой и подробно описан в рамках методики обучения информатике, использовался для определения понятия «задача по информатике» и их классификации) можно считать методологией решения школьных задач по физике с использованием ПК.

Учитывая тот факт, что практически все школьные задачи являются разрешимыми (задачами класса Р), учебный вычислительный эксперимент является подграфом вычислительного эксперимента, не включающий неразрешимые или трудноразрешимые задачи (задачи классов Е или NP соответственно). Учитывая, что существенная часть вычислительного эксперимента, его ядро представлено триадой «модель-алгоритм-программа», то можно считать, что вычислительный эксперимент содержит три основных этапа:

1 этап – Построение математической модели, которая включает в себя: постановку задачи (выделение исследуемого объекта), построение предметной модели (качественной описание выделенного объекта) и построение концептуальной информационной модели, а это все приводит к формулированию некоторой математической задачи, а конкретнее к построению математической модели в виде формальной системы (исчисления).

2 этап – Выделение из математической модели алгоритма, т.е. построение алгоритма решения сформулированной на предыдущем этапе математической задачи, а именно, построение абстрактного вычислительного алгоритма, который может быть выражен либо задачей класса Р, либо задачей класса NP, либо задачей класса Е.

3 этап — Реализация алгоритма. На этом этапе производится построение логической информационной компьютерной модели и реализация алгоритма либо с помощью вычислительной системы (с использованием систем программирования (в частности, написание программы на конкретном языке программирования) и без них, или с помощью метода эвристического поиска), либо без вычислительной системы (тогда реализация построенного алгоритма сводится к "обычному" решению математической задачи). Здесь же происходит построение физической компьютерной информационной модели, а затем анализ результатов (тестирование программы) и принятие решения (фаза прогноза).

Исследовательские занятия и творческие конкурсы-конференции Основным средством приобщения учащихся к творческой деятельности на уроках физики являются исследовательские технологии. При решении различных дидактических задач урока самостоятельные исследования учащихся, построенные на цикле научного познания, являются индикатором не только заинтересованности учебным предметом, но источником научных знаний и методологической компетентности. Оценивание школьных исследовательских проектов осуществляется в ходе творческих конкурсов экспертами по результатам собеседования и защиты на практической конференции.

Дискуссии В современной школе дискуссионные технологии, по праву, считаются инновационными. Они позволяют решать триединую задачу зна-ниевого научения, в ходе которого развиваются различные качества личности: интеллект, самостоятельность решений и суждений, коммуникативность, корректируются интересы школьников с воспитательными и дидактическими целями. Возможности дискуссионных технологий обусловлены рядом психолого-дидактических особенностей школьного возраста: биологически врожденными предпосылками к поисковой активности- основному условию включения ученика в активный творческий и умственный труд; особенностями внутренней мотивации в деятельности и поведении в школьном возрасте: сильно развитым инстинктом общительности, легко возбуждаемым любопытством.

Оценка деятельности учащихся

Приведем типологию форм контроля и оценки достижений учащихся:

Контрольные работы на ПК, с помощью которых определяется относительный уровень знаний и умений учащихся в классах (К-критерий). В работе предполагается выполнить несколько заданий, анализ выполнения и оценка отдельных знаний и умений определяется следующим образом:

знает, умеет, владеет – 1 балл;

не знает, не умеет, не владеет – 0 баллов;

частично знает, умеет, владеет – 0,5 балла.

Задачи оцениваются по следующим позициям, выбор которых зависит от профиля (уровня) обучения (i=l…k):

– обоснование физической модели, границы применимости;

– построение математической модели, ее свойства;

– выбор (анализ) оптимального алгоритма решения (точность, сходимость и устойчивость);

– выбор компьютерных инструментов (систем программирования, математических пакетов, Интернет-ресурсов);

– компьютерная программа (физическая компьютерная информационная модель), тест программы;

– анализ и визуализация результатов вычислительного эксперимента;

– возможность модификации цикла информационного моделирования.

Составляется матрица «успеха» и определяется сумма ее элементов,

далее находится предметная компетентность

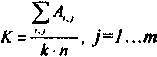- число решенных задач, n - общее число задач цикла, k - позиционное число.

Метод знакового критерия – используется для анализа динамики познавательных интересов учащихся по результатам контрольных работ.

Компьютерным тестированием – проверяются знания основных понятий, законов и формул.

Наблюдения умственной активности

Для регистрации внимания и активности используется метод наблюдений за их внешним проявлением. Во время изложения учебного материала учителем внимание учащихся и их деловая активность являются преимущественно перцептивными (внешне-направленными). Проявление деловой активности легко прослеживается в мимике учащихся, их внешней деятельности. Внешним выражением внимания и деловой активности является всматривание, прислушивание, задержка лишних движений, сосредоточенность и быстрое точное выполнение указаний учителя.

Поминутно отмечая количество внимательных и активных учеников в классе, и параллельно регистрируя форму и содержание обучения в классе, программно-педагогические средства, Интернет-ресурсы получаем данные о внимании и деловой активности на уроке физики, которые обрабатываются методами математической статистики.

Структура деятельности учителя

Предкоммуникативный этап - знакомство с содержанием, оценка Интернет-ресурса, определение целевого назначения и форм организации, разработка дидактического инструментария сопровождения- задания, рабочие листы и пр., мотивация учащихся.

Коммуникативный этап - сопровождение (поддержка), консультирование учащихся.

Посткоммуникативный этап - организация анализа и обсуждения результатов работы, тестирование, оценка выполненных заданий, анализ эффективности использования Интернет-ресурса, рекомендации по совершенствованию для авторов и дальнейшему использованию.

Примеры методических рекомендаций для учителей по работе с Интернет-ресурсом

Оборудование - Интернет-класс, видео-проектор, экран, акустическая система, микрофон, звуковая карта, принтер.

1. Дистанционная поддержка уроков по «Оптике» с использованием Интернет-ресурса «Открытая физика» (mipt.ru/).

Рекомендуется для базового и профильного уровней.

Информационная часть уроков по темам «Поляризация света», «Интерференция света», «Дифракция света», «Разрешающая способность оптических приборов» или обобщающий урок по теме «Волновая оптика».

Учитель: С помощью интерактивных учебных программ демонстрирует виды поляризации света в зависимости от сдвига фаз между двумя взаимно перпендикулярными составляющими электромагнитной волны, опыты по интерференции и дифракции (см. Приложение 2, рис. 1а, б, в, г). Отмечает дидактические преимущества программы: высокая степень наглядности, возможность показать в динамике изменение вида поляризации электромагнитной волны в зависимости от сдвига фаз между двумя взаимно перпендикулярными составляющими электромагнитной волны.

Ученики: Работают с программой, изучая свойства поперечной световой волны. Экспериментируют с компьютерной моделью и отвечают на вопросы, поставленные учителем в ходе урока, а также формулируют собственные вопросы, касающиеся получения и применения поляризованного света и записывают их в тетрадь. Картинки схематично зарисовывают в тетрадь, проводя аналогию с фигурами Лиссажу.

Учитель: В зависимости от цели и задач урока включает интерактивную программу, наглядно демонстрируя двухлучевую интерференцию- опыт Юнга: распределение интенсивности света в интерференционной картине в зависимости от параметров (расстояния между щелями, длины волны излучения). Отмечает, что трудности наблюдения интерференции света в таком опыте связаны с тем, что длина волны видимого света мала. При Д = 5 10 5см и расстоянии между отверстиями, равном всего 0,5 мм, ширина интерференционных полос составляет только 1 мм при удалении экрана на 1 м от отверстий.

Ученики. Проводят виртуальные опыты с когерентными световыми пучками, определяя ширину интерференционной полосы в зависимости от параметров эксперимента. Картинка зарисовывается в тетрадь или распечатывается на принтере. Самостоятельная работа сопровождается ответами на вопросы учителя.

Учитель. Демонстрирует интерференционные полосы равной толщины (Кольца Ньютона) в зависимости от длины волны света и радиуса линзы. Показывает, что подобные демонстрации могут служить необходимым дополнением к натурному эксперименту, требующему определенных навыков юстировки оптических систем.

Ученики- Изучают особенности интерференции света в тонких пленках. Зарисовывают картинку в тетрадь, уточняя ход лучей и условия наблюдения интерференции в отраженном и проходящем свете, записываю (или выводят) формулы для радиусов колец.

Учитель. Компьютерные демонстрации по дифракции света также важны при изучении оптики. Теория дифракции света дает строгое обоснование геометрической оптике и определяет условия ее применимости. В теории дифракции получают свое решение и многие вопросы инструментальной оптики, требующие выхода за рамки геометрической оптики, такие как предельное разрешение оптических систем и спектральных приборов или структура оптического изображения. Удобный интерфейс программы позволяет легко наблюдать дифракцию Фраунгофера на щели и дифракционной решетке, оценивая соотношения интенсивности максимумов. При дифракции на щели высота максимума интенсивности пропорциональна квадрату ширины щели; относительная интенсивность остается неизменной: распределение света по максимумам разных порядков не зависит от ширины шели и быстро убывает с увеличением порядка

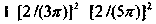. При сужении щели картина расширяется, а ее яркость уменьшается. Когда ширина щели приближается к длине волны, центральный максимум охватывает все поле зрения; освещенность экрана уменьшается от центра к краям монотонно.

Важное практическое применение в спектроскопии имеет явление дифракции Фраунгофера на системе из большого числа одинаковых параллельных щелей, находящихся на равных расстояниях друг от друга (дифракционная решетка) Учитывая, что современные дифракционные решетки обладают очень большим числом штрихов N~200 тыс., изучать образование и свойства дифракционного спектра, не прибегая к сложной для школьников математике, возможно только на компьютерной модели при малых N-10.

Полная напряженность поля световой волны в точке экрана от N периодических элементов решетки представляется суммой геометрической

прогрессии:

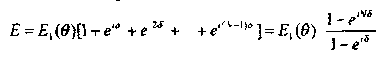
Умножая правую часть на комплексно-сопряженное выражение, получаем интенсивность в данной точке экрана: I(Ө) = I₁(Ө)*

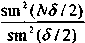. Здесь I₁(Ө) – интенсивность света от одной щели. В результате многолучевой интерференции N когерентных вторичных волн происходит перераспределение светового потока по направлениям и наблюдается существенно отличающееся от I₁(Ө) распределение интенсивности в фраунгоферовой дифракционной картине. Структура отдельного элемента (штриха) решетки сказывается лишь на виде функции I₁(Ө), которая меняется при изменении угла дифракции значительно медленнее, чем второй (интерференционный) сомножитель. Поэтому при большом числе штрихов огибающая функция I₁(Ө) модулирует многолучевую интерференционную картину и определяет относительную интенсивность главных максимумов разных порядков, но практически не влияет на положение и ширину главных максимумов, которая  1/N. Для простой решетки с щелями шириной а и постоянной решетки d интенсивность главного максимума определяется выражением

_.

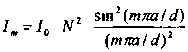Ученики Изучают (повторяют) условия наблюдения дифракции и вид дифракционных картин от разных препятствий Наглядно демонстрируются результаты изучения теоретического материала Отвечают на вопросы учителя о применении дифракции в науке и технике Проводят расчет разрешающей способности дифракционной решетки с возможной проверкой вычислений в натурном эксперименте. Создают проблемную ситуацию для исследования работы оптических приборов (телескопа, микроскопа, спектроскопа), их аппаратных функций.

Учитель Рассмотрим пример из техники спектроскопии. Реальные возможности спектрального прибора, позволяющие более или менее детально исследовать оптический спектр, в значительной степени определяются шириной и формой его инструментального контура. Для характеристики этих возможностей вводится понятие разрешающей способности прибора. Возможность разделить две близкие монохроматические линии зависит от точности, с которой измерен инструментальный контур и может быть измерен наблюдаемый контур. Поэтому количественный критерий разрешающей способности можно сформулировать только условно в предположении определенной точности энергетических измерений распределения интенсивности.

В ходе демонстрационных экспериментов учитель подчеркивает, что детальное изучение фундаментальных вопросов экспериментальной физики в школе невозможно без использования имитационно-моделирующих программ. Весьма убедительно в программе «Открытая физика» демонстрируется условный критерий Рэлея, удобный для сравнения разрешающей силы различных спектральных приборов, для случая, когда инструментальный контур имеет дифракционную форму, т.е. учитываются дифракционные эффекты в оптической системе.

3. Парадоксы как средство развития физического мышления

(см. учебные ресурсы на сайтах по адресам. ge.ru/physics/index.php, nw.ru).

Последовательная реализация концепции «образование как учебная модель науки» требует адекватного представления в процессе обучения физике всех основных компонентов; методологического и научного исследования; отражения модельного характера научных представлений о реальном мире; развития физического мышления как способности анализировать любую непонятную ситуацию. Особое место занимает умение разбираться в физических парадоксах, которыми усеян весь исторический путь развития физики от гидростатического парадокса известного с давних времен, до парадоксов в современной квантовой физике (см. Приложение 2, рис. 5).

Учитель: Рассказывает о сути научных парадоксов, дает их классификацию. При всей условности классификации физических парадоксов можно выделить два основных класса парадоксов:

1) парадоксы, возникающие в результате логических или методологических ошибок в рассуждениях или интерпретации результатов,

2) парадоксы, не связанные с какими-либо ошибками в рассуждениях, а возникающие вследствие выхода за рамки применимости использования физической модели или ее внутренней противоречивости.

Парадокс является непременным атрибутом любой физической теории, и вопрос может стоять только о педагогической и математической целесообразности явного представления определенного парадокса, или его адекватных методов рассмотрения. При этом разбор парадокса и выявления причин его появления является одним из наиболее эффективных средств развития физического понимания.

(Примечание Оригинальность и наглядность необходимы для того, чтобы максимально заинтересовать учащихся предложенным парадоксом, вызвать у них глубокие эмоциональные переживания, удивление каким - либо несоответствием. Примером, подтверждающим данное требование, может служить парадокс Паскаля и гидростатический парадокс, изучаемый в теме: "Гидро- и аэростатика").

Ученики Выводят формулу гидростатического давления методом размерностей. Решают задачи на закон Архимеда

Учитель Модельный характер научных знаний убедительно подтверждает история развития квантовой физики.

Парадокс, связанный с корпускулярно-волновым дуализмом квантовой механики, требует ответа на вопрос, что же всё-таки такое свет или электрон - частица или волна? Некоторые оптические явления свидетельствуют в пользу волновых представлений, другие могут быть объяснены только с корпускулярной точки зрения. Наконец, существует целый ряд оптических явлений, которые допускают объяснение как с точки зрения волновых, так и с точки зрения корпускулярных представлений о свете. Рассматривая несколько конкретных примеров - явление интерференции, когерентность света, эффект Доплера и т д., мы можем убедиться, что при анализе этих конкретных явлений двойственная природа света никак не мешает нашим рассуждениям и не приводит к логическим противоречиям. Нужно только выбрать, на волновом или корпускулярном языке вести рассмотрение, и последовательно придерживаться выбранного способа описания Противоречие возникает только тогда, когда делается попытка составт ь общее представление о свете. (Примечание Методика рассмотрения парадокса, связанного с корпускулярно-волновым дуализмом, должна подчеркивать принципиальный характер этого обстоятельства и демонстрировать неизбежность отказа от представлений классической физики).

Ученики Изучают компьютерные опыты и решают задачи по темам: «Тепловое излучение», «Фотоэффект», «Эффект Комптона», «Атом водорода и постулаты Бора».

(Примечание: Краткость и простота решения парадокса, как и требование наглядности, основаны на особенностях развития познавательных процессов детей подросткового возраста: высокая концентрация внимания, но низкая устойчивость; наиболее развита образная и эмоциональная память, словесно-логическая только начинает развиваться. В силу этого учащимся очень трудно следить за логико-математическими доказательствами какого-либо закона, явления, если его приводит учитель. А еще труднее сделать этот вывод им самостоятельно).

Развитие мышления учащихся в процессе решения физических парадоксов, так же как и во всякой умственной деятельности, требует применения всей совокупности форм и методов научного познания: наблюдений, эксперимента, сравнений, выдвижения гипотез, использования аналогий, индукции и дедукции, анализа и синтеза. При этом суть парадокса, как решения некоторой проблемы заключается в установлении причинно-следственных связей и зависимостей. Физические парадоксы должны занять особое место в компьютерной поддержке учебного процесса, т.к. они являются одной из наиболее эффективной формой углубленного изучения и закрепления теоретического материала, развития физического понимания.

4. Автоматизация учебного физического эксперимента. Опыты со звуком на основе компьютерного мультимедийного комплекса.

(см. Интернет-ресурс по адресу system.ru/soft/editor/sound forge.php).

Учитель: Рассказывает основы автоматизации физического эксперимента. Современный мультимедийный компьютер при наличии соответствующего оборудования (hardware и software) может превратиться в измерительный комплекс весьма удобный для организации и проведения учебного физического практикума. Клавиатура ПК и экран монитора предоставляют большие возможности по сравнению с теми, которые могут дать физические приборы, например, гальванометр или осциллограф, а дисковод и принтер прекрасно подходят для регистрации изучаемых процессов. Кроме того, вычислительная мощность компьютера позволяет подвергать собранные с его помощью информационные данные достаточно сложной обработке, например, спектральному анализу колебаний струны.

Ученики: Наблюдают сигнал и амплитудный спектр колебаний струны, а также зависимость колебаний от способа возбуждения. По «осциллограмме» определяют частоту основного тона, рассчитывают обертона и сравнивают с экспериментальными данными Самостоятельно работают с демонстрационным комплексом по акустике, выполняя задания учителя.

(Примечание Демонстрационный комплекс по акустике включает программы Analysis center, Audio Tester, Sound Forge, WaveLab).

Демонстрационный комплекс включает в себя оснащенный звуковой картой компьютер, микрофон, колонки и компьютерную программу, выполняющую функции управления комплексом, обработки аудио сигналов и демонстрации результатов. Программа работает в операционной системе Windows и использует только ее стандартные функции, что позволяет легко переносить программу с одного компьютера на другой.

«Гаммы». Демонстрируются спектры и осциллограммы звуков, различной высоты, извлекаемых из различных музыкальных инструментов. Музыкальный инструмент для проигрывания гаммы выбирается из выпадающего списка, скорость проигрывания может регулироваться.

«Анализ звуков». Демонстрируются спектры и осциллограммы различных звуков, в частности, гласных и согласных звуков человеческой речи Для демонстрации необходимо подключить к входу звуковой карты компьютера микрофон.

«Фазовый состав». Демонстрируется нечувствительность человеческого уха к фазовому составу звука, т е. к соотношению между фазами отдельных гармоник, синтезируется звук, состоящий из двух гармоник одинаковой мощности, отличающиеся друг от друга по фазе. Сдвиг фаз между гармониками регулируется при помощи мыши или клавиатура. В то время как осциллограмма заметно меняется при изменении разности фаз между гармониками, спектр и слышимый звук остаются неизменными

«Бинуаральный эффект». Демонстрируется бинуаральный эффект, позволяющий человеку определять направление на источник звука на низких частотах основную роль играет сдвиг фаз между сигналами, воспринимаемыми ушами. Генерируются два гармонических сигнала одинаковой частоты и мощности с регулируемой разностью фаз, каждый из которых подается на свой стереоканал При изменении сдвига фаз у наблюдателя создается ощущение смещения источника звука.

«Эквидистантные частоты» Демонстрируется результат сложения гармоник одинаковой мощности с эквидистантными частотами. Задавая различные значения базовой частоты и шага и изменения число гармоник, можно получать биения, короткие импульсы и т.д. При этом наблюдатель видит спектр, осциллограмму и слышит соответствующий звуковой сигнал.

Физический практикум по акустике может быть дополнен рядом других опытов и демонстраций, например, для физико-математического профиля — «Фигуры Лиссажу», «Измерение скорости звука в воздухе», элективный курс для физико-биологического профиля «Психофизика слуха».

Инновационное обучение физике (Проекты и деловые игры для старшеклассников)

Приведем несколько адресов Интернет-ресурсов по данной тематике (enta.ru, www delphimaster.ru, http7/pascal dax ru)

Компьютерные проектные и игровые технологии значительно расширяют возможности вариативной школы в плане формирования индивидуальных образовательных маршрутов учеников. Учащимся, увлекающимся компьютерной графикой и теоретической физикой, можно предложить задачи компьютерно-графического моделирования в классической или квантовой механике с использованием пакетов символьной математики.

«Квантовая модель атома» Рекомендуется для профильного уровня или для элективного курса (физико-математический, химико-физический профили).

Учитель Излагает теорию вопроса, демонстрируя конфигурации атомов при разных квантовых числах.

Многоэлектронные атомы представляют собой сложную систему взаимодействующих друг с другом электронов, движущихся в поле ядра. Последовательный квантово-механический подход требует рассматривать атомную систему как единое целое и использовать для ее описания многопараметрическую волновую функцию. Тем не менее, оказывается, что в атоме можно с хорошей точностью ввести понятие о состояниях каждого электрона в отдельности как о стационарных состояниях движения электрона в некотором эффективном центрально-симметричном поле, созданном ядром вместе со всеми остальными электронами. Для различных электронов в атоме эти поля, вообще говоря, различны, причем определяться они должны одновременно все, поскольку каждое из них зависит от состояний всех остальных электронов. Такое поле называется самосогласованным. Данная квантовая модель атома в приближении Хартри-Фока может рассматриваться, как обобщенная задача об атоме водорода.

Ученики Знакомятся с демонстрационными моделями квантовой механики и методами программирования в компьютерной среде Maple. Выполняют дифференцированные самостоятельные задания по компьютерному моделированию электронных оболочек атома с использованием прикладных математических и графических пакетов.

4 «Измерение кровяного давления (гемодинамика капилляров)».

Учитель: Осуществляет постановку задачи и контролирует ход ее решения.

Сердечно-сосудистая система предназначена для доставки обогащенной кислородом крови к тканям организма. Непосредственный обмен веществ между кровью и тканями осуществляется через стенки капилляров. Транскапиллярный обмен определяется, прежде всего, гемодинамическими параметрами кровотока и ультраструктурой капиллярной стенки. В общем случае гемодинамические функции давления, объемной скорости потока, завися друг от друга, являются нелинейными. Для того, чтобы найти функции Р(х), Q(x), q(x) воспользуемся методами математического моделирования в рамках ньютоновской гидродинамики. Рассмотрим два одновременно протекающих процесса в системе «капилляр-ткань»: движение жидкости вдоль капилляра и поперек через поры в его стенке. При этом капилляр рассматриваем как жесткую трубку с гидравлическими порами в ее стенке. Допустим, что по такой трубке течет ньютоновская жидкость с растворенными в ней солями. Будем считать, что пульсации кровотока в микрососудах отсутствуют.

Ученики. В ходе теоретического исследования получают аналитическое решение

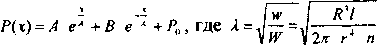
(коэффициенты А и В находятся из граничных условий). В ходе вычислительного эксперимента убеждаются в том, что численный метод Эйлера оказывается неустойчивым в классе краевых задач. А это означает, что для получения достоверных результатов необходимо прибегнуть к более сложным алгоритмам или воспользоваться возможностями прикладных математических пакетов. Используя асимптотику L/  0 (квазисплошной сосуд) из общего решения приходят к линейному закону Пуазейля знакомому из гидродинамики.

5. «Изучение эпидемии гриппа в школьном классе».

Учитель: Осуществляет постановку трудно формализуемой задачи биофизики с использованием метода балансовых соотношений на примере одной из линейных моделей детских эпидемий.

Модель состоит из трех компонент: 1) детей, восприимчивых к заболеванию x(t) - «группа риска», 2) инфекционные, больные дети, являющиеся источником распространения болезни y(t), 3) выздоровевшие дети и обладают иммунитетом к данной болезни z(t). Причем, в замкнутой системе x(t)+y(t)+z(t)=N. Предполагается далее, что в случае, когда число инфекционных людей превосходит некоторое значение у(t)>у^* (много инфекционных детей в школе), скорость изменения числа детей в «группе риска» пропорциональна числу детей, т.е. x(t) = -*x(t), в противном случае y(t)  у^* , x(t) = 0.

Таким образом, принимается во внимание факт изоляции инфекционных детей (карантин). Теперь, поскольку заболевший человек, является инфекционным, то скорость изменения числа инфекционных детей представляет разность за единицу времени между заболевшими и теми, которые уже выздоравливают. Итак, y(t) = *x(t)-*y(t), если y(t)>y^* и y(t) = -*y(t), если y(t) £ у^*, где постоянные  и  – коэффициенты заболеваемости и выздоровления соответственно. Наконец, скорость изменения числа выздоравливающих детей задается уравнением z(t) = *y(t). Для простоты выберем начальные условия z(0) = 0 и у(0) = у₀ и положим  = .

В случае «карантина» у₀ £ у^* (много инфекционных детей в изоляции) решение система дифференциальных уравнений имеет простые аналитические решения:

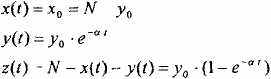
На начальном этапе эпидемии у₀ > у^* (много инфекционных детей в школе) анализ модели для учащихся связан с математическими трудностями, поэтому для решения задачи необходимо воспользоваться численными методами

Ученики Изучают предельные случаи задачи аналитическими и численными методами в распространенных средах компьютерного моделирования Обсуждают результаты вычислительного эксперимента

Дидактические игры

Рекомендуются для организации самостоятельной работы (поисковые системы Интернет Yandex, Yahoo, Rambler Апорт1 AltaVista).

«Компьютерное домино» (молекулярная физика, термодинамика) – для 10-11 класса, «Опыт Резерфорда» и математическое домино на тему «Типы функций».

«Спираль слов» Правило игры следующее: нужно распутать спираль слов, где последняя буква каждого слова служит первой буквой следующего. Игру «Спираль слов» можно использовать на одном из этапов урока – закрепление изученного материала, для того, чтобы разнообразить урок и для лучшего усвоения материала, так как игра всегда создает положительный эмоциональный фон и желание учащихся самоутвердиться

«Игра Баше» Смысл игры заключается в следующем пусть имеется, например, 30 предметов (спичек, пуговиц и т.д.) Играют двое (ученик и компьютер) и берут поочередно любое количество предметов, например, от 1 до 6. Именно Баше, французский ученый-энциклопедист (1581–1638), открыл выигрышную стратегию для того, кто начинает игру первым. Имеется два варианта игры Баше: 1) проигрывает тот, кому приходится брать последний предмет, 2) выигрывает тот, кому приходится брать последний предмет. Проигравшим предлагается тест на компьютере по физике из Интернет-ресурсов. Игра необходима для того, чтобы между учащимися и компьютером установились доверительные отношения, чтобы ученик понимал, что ПК - интеллектуальная машина, которую сложно обмануть.

В Интернет-тестировании (см Интернет-ресурсы по адресам http//www.ht.ru, http//www.teletesting.com, http//www.education.spb.ru) используются, как правило, традиционные формы диалога с компьютером закрытый (ответ «да» или «нет»), ограниченный (наличие нескольких альтернатив ответа, обычно k=2-5)/ В проектировании и использовании «быстрых» тестов необходимо учитывать математическую статистику диалога. Моделируя диалог с компьютером независимыми испытаниями Бернулли, можно оценить вероятность «случайного успеха» P_n(m) =С_n^mр^mqⁿ^-^m (биномиальный «успех»). Здесь n - число задач, m - общее число случайных правильных ответов, р=1/k вероятность правильного ответа при решении одной задачи (в одном испытании), q=l-p При больших n пользоваться формулой Бернулли затруднительно, поэтому удобнее воспользоваться асимптотикой Лапласа

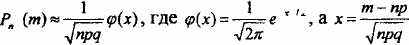
«Алгоритмическая игра «Ванька-встанька» Учебно-игровое моделирование расширяет дидактический арсенал учителя физики созданием проблемных ситуаций на уроке при изучении теоретического материала в старших классах, при углубленном изучении физики Алгоритмические игры могут быть реализованы с помощью распространенной математической системы Maple Эта система удобна использованием интерфейса типа «рабочего листа» команды пишутся красным цветом, результат выполнения команд -синим, присутствует качественная интерактивная графика, эффекты анимации, средства «помощи», комментарии

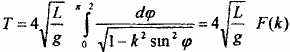
Учитель: Рассказывает кинематику математического маятника в качестве физической модели игрушки «Ванька-Встанька», приводящей к формуле для периода колебаний в виде

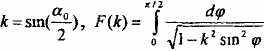- эллиптический интеграл первого рода является стандартной спецфункцией популярной компьютерной системы Maple. Программирование итерационных алгоритмов позволяет оценить точность вычислений В частности, для n=10 (₀=45 град.) погрешность численного метода составляет _n~0.5%, а при n=45 _n ~ 0.05 %.

Ученики: Исследуют временную зависимость угла отклонения «маятника» и его фазовую траекторию в зависимости от начальных условий и параметров задачи. Моделируют натурный эксперимент по измерению ускорения свободного падения с помощью математического маятника.

Blog