Моделирование
| Вид материала | Документы |
- Моделирование и формализация Моделирование как метод познания Моделирование, 143.04kb.
- Календарный план учебных занятий по дисциплине Моделирование информационных процессов, 24.12kb.
- Темы курсовых работ по дисциплине «моделирование систем» Ваш № в списке группы, 19.48kb.
- ИнтервальноЕ моделирование свойств сплава, 16.17kb.
- Программа спецкурса "Компьютерное моделирование нелинейных волновых процессов" Специальность, 27.11kb.
- Лекция Моделирование физических процессов, 111.71kb.
- Программа дисциплины имитационное моделирование в экономике для направления 080100., 228.47kb.
- Правительстве Российской Федерации» (Финансовый университет) Кафедра «Математическое, 246.23kb.
- Лекции по дисциплине «Социальное моделирование и программирование», 44.69kb.
- Учебно-методический комплекс по дисциплине "компьютерное моделирование" (факультет, 384.08kb.
12. Модель одноканальной СМО с ограниченной очередью.
Рассмотрим простейшую задачу: исследуемая СМО одноканальная (n=1) с ограниченным числом m мест в очереди, поток заявок стационарный пуассоновский с интенсивностью λ, время обслуживания распределено по показательному закону с параметром μ. Заявка, поступившая в момент, когда канал занят, становится в очередь, если ее длина (количество заявок в очереди) не превышает m. В противном случае заявка получает отказ и покидает систему необслуженной, т. е. рассматривается СМО вида М|М|1|m.
Система в произвольный момент времени может оказаться в одном из состояний:
So - канал свободен, очереди нет,
S1 – канал занят, очереди нет,
S2 - канал занят, в очереди одна заявка,
…
Sk - канал занят, к-1 заявка в очереди,
…
Sm+1 - канал занят, m заявок в очереди.
Размеченный граф состояний системы представлен на рис. 4. В графе всего m+2 состояния. Система переходит из состояния Si в состояние Si+1 под воздействием потока заявок с интенсивностью λ, и, наоборот, из состояния Si+1 она переходит в состояние Si под воздействием потока обслуженных заявок с интенсивностью μ.
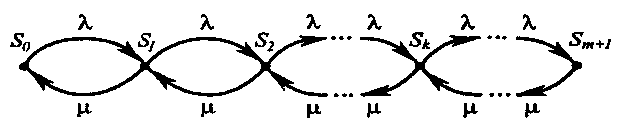
Рис. 4. Граф состояний одноканальной СМО с очередью
Пользуясь общим решением для схемы «размножения и гибели», можно, введя обозначение ρ=λ/μ, записать выражения для предельных вероятностей состояний:
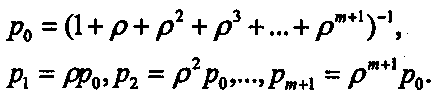
Или в более компактной записи:
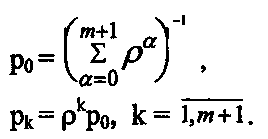 (19)
(19)В выражении для р0 формулы (19) суммируются члены геометрической прогрессии 1, ρ, ρ2, … , ρm+1. Используя формулу суммы членов прогрессии, можно записать:
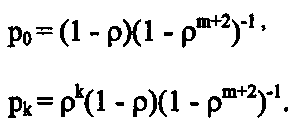 (20)
(20)Теперь можно последовательно определить основные характеристики эффективности СМО: Ротк , q, A, r - среднее число заявок, находящихся в очереди, k - среднее число заявок, связанных с системой (стоящих в очереди и обслуживаемых), tож - среднее время ожидания заявки в очереди и tсист - среднее время пребывания заявки в системе.
Вероятность отказа в обслуживании
 (21)
(21)так как pm+1 — вероятность того, что канал занят и все m мест в очереди заняты.
Относительная пропускная способность
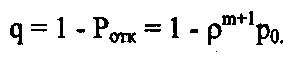 (22)
(22)Абсолютная пропускная способность
Α=λq. (23)
Среднее число заявок, находящихся в очереди — r. Рассмотрим случайную величину R — число заявок в очереди, закон распределения которой следующий: с вероятностью р2 в очереди находится одна заявка (R = 1), с вероятностью р3 — две заявки (R = 2), с вероятностью pm+1 — m заявок (R = m). Тогда
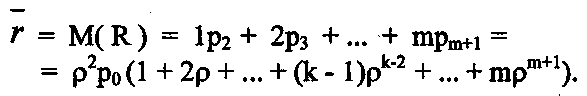
В полученном выражении в скобках находится сумма некоторых слагаемых. Нужно вывести формулу для этой суммы, которая представляет собой производную по ρ следующего выражения:
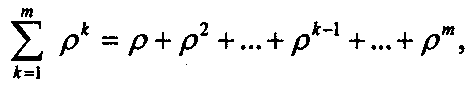
а уже для полученного выражения можно использовать формулу суммы геометрической прогрессии:
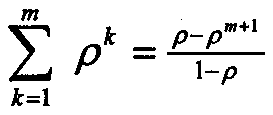
После некоторых преобразований и упрощений можно получить выражение для среднего числа заявок, находящихся в очереди:
 (24)
(24)Среднее число заявок, связанных с системой (стоящих в очереди и обслуживаемых) — k . Нужно рассмотреть случайную величину К = R + Ω, где К — число заявок, связанных с системой, R — число заявок в очереди, Ω — число заявок, находящихся на обслуживании. Тогда
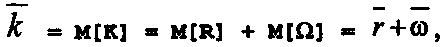
где r вычисляется по формуле (24), а выражение для ω необходимо вывести.
В исследуемой системе используется один канал, поэтому случайная величина Ω принимает лишь два значения: 0 – с вероятностью ро = (1 - ρ)(1 – ρm+2)-1 , когда канал свободен; 1 — с вероятностью 1 - Ро, когда канал занят:
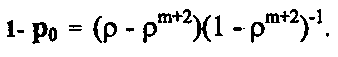
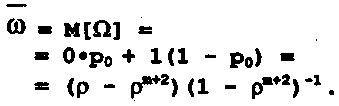 (25)
(25)Среднее время ожидания заявки в очереди tож. Если учесть, что среднее время обслуживания одной заявки равно l/μ, то, рассматривая случайную величину Тож — время ожидания в очереди, можно определить закон распределения этой случайной величины: с вероятностью p1 заявка придет в систему во время обслуживания предыдущей заявки, но перед ней не будет очереди, и она будет ждать начала обслуживания в течение времени Тож = l/μ; с вероятностью р2 в очереди перед рассматриваемой заявкой будет стоять еще одна, и время ожидания Тож = 2/μ и, наконец, с вероятностью рк пришедшая заявка застанет в системе к заявок и будет ждать Тож = k/μ единиц времени. Поэтому
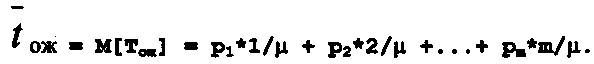
Подставляя в полученное выражение Pk (k = 1… m), а затем, сделав некоторые преобразования, можно записать:
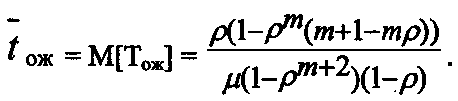 (26)
(26)Выражение (26) с учетом (24) записывается в упрощенном виде:
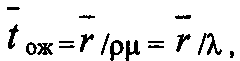
т. е. среднее время ожидания равно среднему числу заявок в очереди, деленному на интенсивность потока заявок.
Среднее время пребывания заявки в системе tсист.
Для определения tсист нужно ввести случайную величину Тсист — время пребывания заявки в СМО: Тсист=Тож+Θ, где Тож - время ожидания заявки в очереди; Θ — случайная величина, равная времени обслуживания Тобс, если заявка обслуживается и нулю если она не обслуживается (получает отказ). Таким образом,
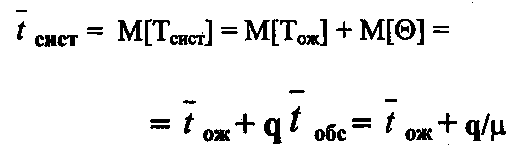
или иначе, с учетом (27):
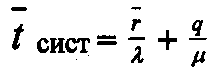 (28)
(28)13. Модель одноканальной СМО с неограниченной очередью.
Рассмотрим работу одноканальной СМО (n=1) с ожиданием для случая, когда число мест в очереди не ограничено (m=∞). Процесс функционирования такой системы описывается путем предельного перехода от системы М|М|1|m при m→∞, т.е. будет рассматриваться система М|М|1|∞ (рис. 5). Этот предельный режим может существовать только при ρ < 1
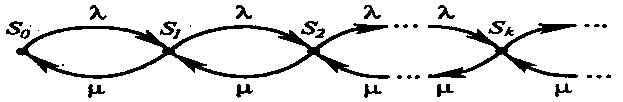
Рис. 5. Граф состояний одноканальной СМО с неограниченной очередью.
(μ > λ), так как в формуле (19) представлена сумма бесконечного числа членов геометрической прогрессии. При ρ >= 1 очередь растет до бесконечности. Поэтому в дальнейшем полагают, что ρ < 1, тогда из формул (19) при m→∞ получают, что сумма прогрессии
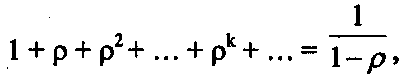
откуда
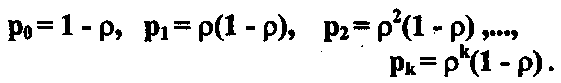 (29)
(29)Вероятности р0, p1, p2, ..., pk, … образуют геометрическую прогрессию со знаменателем ρ. Максимальная из них ро — вероятность того, что канал будет вообще свободен. Это свидетельствует о том, что как бы ни была нагружена система с очередью, если она только вообще справляется с потоком заявок (ρ<1), самое вероятное число заявок в системе будет равно нулю.
Основные показатели эффективности для системы М|М|1|∞ определяются по следующим формулам, полученным путем предельного перехода при m→∞ из соответствующих формул для системы М|М|1|m:
Pотк = 0,
так как при отсутствии ограничений по длине очереди каждая заявка, пришедшая в систему, будет обслужена:
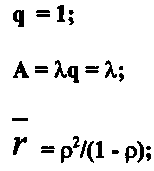 (30)
(30)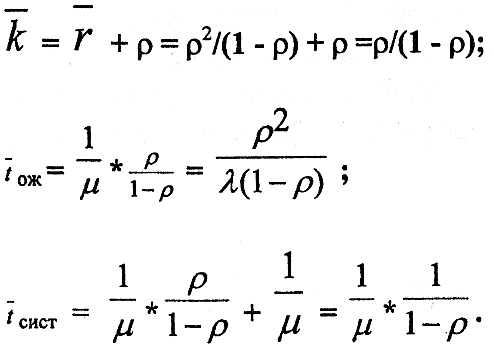
14. Модель многоканальной СМО с ограниченной очередью.
Схема рассматриваемой СМО имеет вид: M|M|n|r=m.
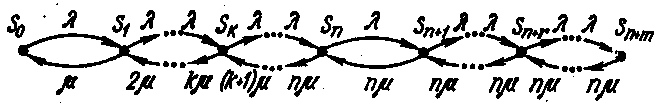
Рис. 6. Граф многоканальной СМО с ограниченной очередью
Размеченный граф состояний представлен на рис. 6. Пользуясь формулами процесса «размножения и гибели», можно записать:
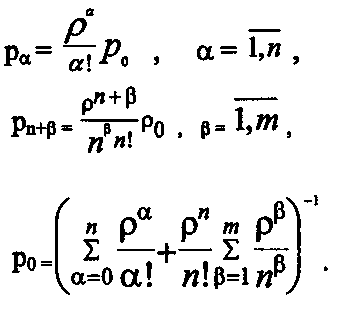 (31)
(31)Последние m слагаемых в выражении для р0 (31) являются членами геометрической прогрессии со знаменателем ρ/n ,поэтому
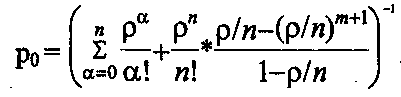 (32)
(32)Определим характеристики эффективности рассматриваемой СМО:
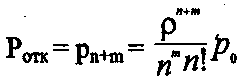 (33)
(33)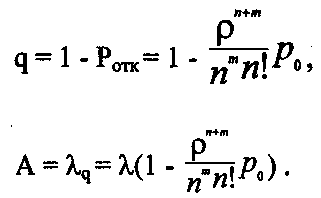 (34)
(34)Для нахождения среднего времени ожидания заявки в очереди tож нужно рассмотреть случайную величину G, которая принимает значения (r+1)/nµ с вероятностями рn+r, для r = 0,m-1 :
 (35)
(35)Для нахождения среднего числа заявок, ожидающих начала обслуживания r, рассматривается дискретная случайная величина R, принимающая значения r с вероятностью рn+r для r =1,m:
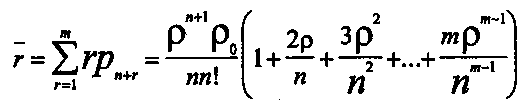 (36)
(36)Выражение (35) с учетом (36) можно переписать:
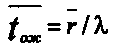 (37)
(37)В выражениях (35) и (36) в скобках находится производная по ρ/n суммы членов геометрической прогрессии
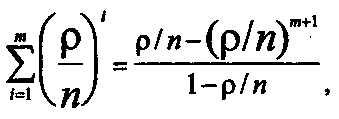
дифференцируя которую по ρ/n и делая некоторые преобразования, получают:
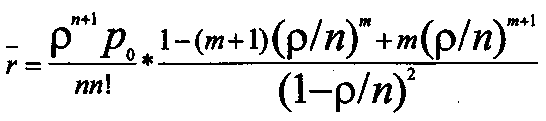 (38)
(38)Аналогичным образом можно получить выражение для tож.
Среднее число занятых каналов z определяется с учетом того, что каждый занятый канал обслуживает в среднем μ заявок в единицу времени, а вся СМО обслуживает А заявок, тогда
 (39)
(39)Среднее число заявок k, связанных с системой, определяется с учетом выражений (38) и (39):
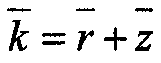 (40)
(40)Для нахождения среднего времени пребывания заявки в системе можно, используя выражение (37), записать:
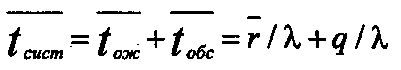 (41)
(41)15. Модель многоканальной СМО с неограниченной очередью.
Пусть в СМО, состоящую из n каналов, поступает простейший поток заявок с интенсивностью λ, время обслуживания одной заявки подчинено показательному закону распределения с параметром μ. Размеченный граф состояний таких систем Μ|Μ|n|∞ имеет бесконечное число состояний (рис. 7).
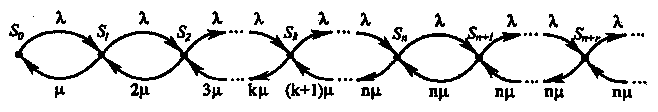
Рис. 7. Граф многоканальной СМО с неограниченной очередью.
Используя формулы (31) и (32), получают вероятности состояний для рассматриваемой системы М|М|n|∞, осуществляя предельный переход (m→∞):
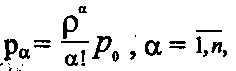
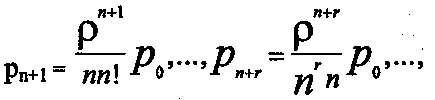 (42)
(42)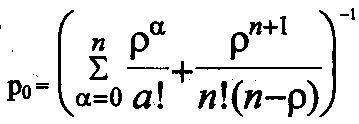
Выражение для р0 в формулах (42) получено в предположении, что ρ/n < 1, так как только при этом существует установившийся режим, а при ρ/n ≥ 1 очередь бесконечно возрастает.
Для данной системы Ρотк = 0, q = 1, А = λ, r находится из (38) при m→∞.
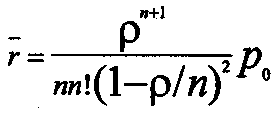 (43)
(43)Из (35) и (37) или из (43) среднее время ожидания
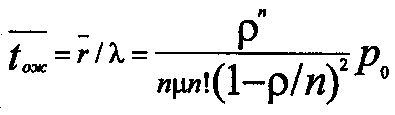 (44)
(44)Среднее число занятых каналов Ζ = Α/μ = ρ. Среднее число заявок, связанных с системой, k = r + Z, а среднее время пребывания заявок в СМО tсист = tож + 1/µ.
