Моделирование

Вид материала

Документы

Содержание 8. Расчет вероятностей состояний однородной Марковской цепи. 9. Уравнения Колмогорова для вероятностных состояний.

Подобный материал:

• Моделирование и формализация Моделирование как метод познания Моделирование, 143.04kb.
• Календарный план учебных занятий по дисциплине Моделирование информационных процессов, 24.12kb.
• Темы курсовых работ по дисциплине «моделирование систем» Ваш № в списке группы, 19.48kb.
• ИнтервальноЕ моделирование свойств сплава, 16.17kb.
• Программа спецкурса "Компьютерное моделирование нелинейных волновых процессов" Специальность, 27.11kb.
• Лекция Моделирование физических процессов, 111.71kb.
• Программа дисциплины имитационное моделирование в экономике для направления 080100., 228.47kb.
• Правительстве Российской Федерации» (Финансовый университет) Кафедра «Математическое, 246.23kb.
• Лекции по дисциплине «Социальное моделирование и программирование», 44.69kb.
• Учебно-методический комплекс по дисциплине "компьютерное моделирование" (факультет, 384.08kb.

8. Расчет вероятностей состояний однородной Марковской цепи.

Пусть известны вероятности Р_ij перехода за один шаг системы S из состояния S_i в состояние S_j (где i, j = 1…n). Причем Р_ij есть вероятность задержки системы в состоянии S_i. Эти вероятности удобно записывать в виде квадратной матрицы Π переходных вероятностей



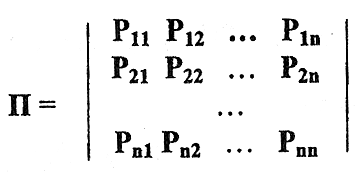
Некоторые элементы Р_ij этой матрицы могут равняться нулю, если невозможен переход системы за один шаг из состояния S_i в состояние S_j.

Переходные вероятности Р_ij можно записать как условные вероятности:



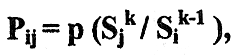
т.е. Р_ij есть условная вероятность того, что система S будет в состоянии S_j на k-м шаге при условии, что она была в состоянии S_i на k-1-м шаге. Из этого следует, что для всех i=1…n



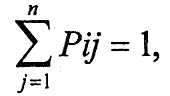
так как для любого k события (состояния) S_i^(k) (i=1…n) несовместны и образуют полную группу.

При использовании графа состояний марковской цепи на нем у стрелок обычно ставят соответствующие переходные вероятности Р_ij. Такой граф называется размеченным.



На графе, чтобы не загромождать рисунок, не проставлены вероятности Р_ii (i=1…n), но они легко вычисляются, так как любой диагональный элемент матрицы переходных вероятностей дополняет до единицы сумму элементов соответствующей строки:



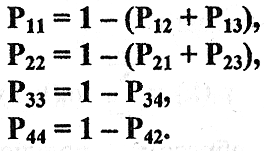
Если же из i-й вершины графа не выходит ни одной стрелки, то это свидетельствует о том, что Р_ii=1.

Как определить вероятности состояний P_i(k) (i=1…n) после любого k-го шага, если известна матрица переходных вероятностей и известно начальное состояние системы S?

Пусть известно, что перед первым шагом (в начальный момент времени) система S находится в состоянии S_m. Тогда для момента времени t_k=0 можно записать р_m(0) = 1, a



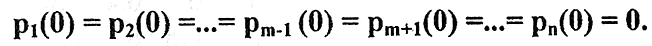
Теперь можно определить p_i(1) (i=1…n). Известно, что перед первым шагом система была в состоянии S_m , поэтому за 1-й шаг она перейдет в состояние S_i с вероятностями Р_mi , которые находятся в m-й строке матрицы Π = |Р_ij|, т.е. p_i(1) =P_mi(i=1…n), или иначе



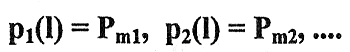
Вероятности состояний после второго шага P_i(2) нужно рассчитывать по формуле полной вероятности с учетом того, что после первого шага система S могла быть или в состоянии S₁, или S₂, или S₃ и т.д. Поэтому по формуле полной вероятности для состояния S_i можно записать:



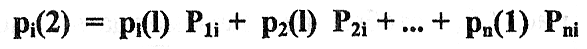
или в сокращенном виде:



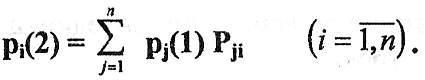
После k-го шага



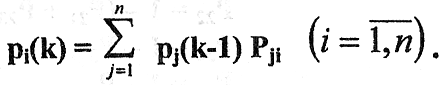
Таким образом, получена рекуррентная формула определения вероятностей состояний системы S после k-гo шага по рассчитанным вероятностям состояний для (k-1)-го шага.

9. Уравнения Колмогорова для вероятностных состояний.

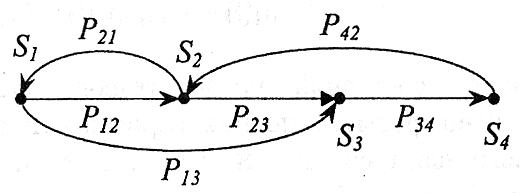
Если известны вероятности перехода λ_ij для всех пар состояний Si и Sj, то, построив граф состояний системы S, удобно против каждой дуги графа ставить соответствующее значение λ_ij. Получится размеченный граф состояний (рис.1). Имея в распоряжении размеченный граф состояний системы, легко построить математическую модель данного процесса, а по модели определить вероятности состояний p_i(t). Для этого составляются и решаются так называемые уравнения Колмогорова. Методика их составления может быть легко продемонстрирована на конкретном примере.



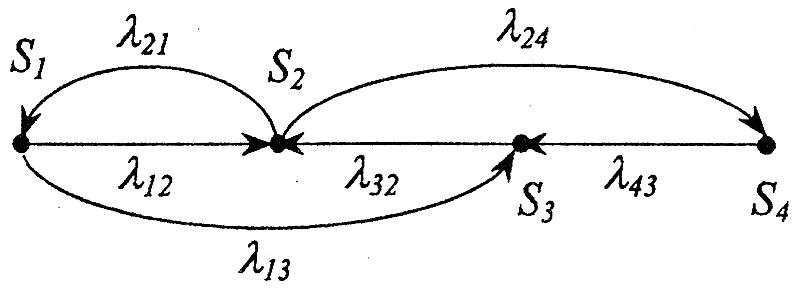
рис.1

Пусть система S имеет четыре возможных состояния: S1, S2, S3, S4 (рис.1). Как найти одну из вероятностей состояний, например, p1(t), т.е. какова вероятность того, что в момент t система будет в состоянии S1. Для этого времени t дается малое приращение t+Δt и находится вероятность p1(t+Δt) того, что в момент t+Δt система будет в состоянии S1. Это может произойти двумя способами (в соответствии с рис.1):

1. если в момент t система была в состоянии S1, то за Δt она не вышла из него;
   
2. если в момент t система была в состоянии S2, то за Δt она перешла из S2 в S1.
   

Для первого случая искомая вероятность равна произведению вероятности p1(t) на условную вероятность того, что из состояния S1 система за время Δt не перейдет ни в S2, ни в S3. Вероятность того, что за Δt система выйдет из состояния S1 равна (λ₁₂+λ₁₃)Δt, а вероятность того, что не выйдет: 1-(λ₁₂+λ₁₃)Δt. Тогда для первого случая вероятность равна p1(t)(1-(λ₁₂+λ₁₃)Δt).

Для второго случая – равна вероятности того, что в момент времени t система была в S2, а за Δt перешла в S1, т.е. она равна p2(t)λ₂₁Δt. По правилу сложения вероятность

p1(t+Δt) = p1(t)(1-(λ₁₂+λ₁₃)Δt) + p2(t)λ₂₁Δt .

Перенося p1(t) в левую часть полученного уравнения и деля обе части его на Δt, можно записать:

(p1(t+Δt) - p1(t)) / Δt = λ₂₁p2(t) - (λ₁₂+λ₁₃)p1(t) .

Далее, переходя к пределу, получают дифференциальное уравнение:

dp1/dt = λ₂₁p2 - (λ₁₂+λ₁₃)p1 . (1)

Подобным образом можно привести еще одно уравнение для вероятности состояния p2(t). Для этого рассматривают состояние S2 и находят p2(t+Δt), учитывая, что в S2 система могла перейти одним из следующих способов:

1. в момент t система была в состоянии S2 и за Δt не перешла из этого состояния ни в S1, ни в S4;
   
2. в момент t система была в состоянии S1 и за Δt она перешла в S2;
   
3. в момент t система была в состоянии S3 и за Δt перешла в S2.
   

Вероятность первого варианта: p2(t)(1-(λ₂₁+λ₂₄)Δt); вероятность второго варианта: p1(t)λ₁₂Δt; третьего варианта: p3(t)λ₃₂Δt. Складывая полученные варианты и приравнивая их p2(t+Δt), получают:

p2(t+Δt) = p2(t)(1-(λ₂₁+λ₂₄)Δt) + p1(t)λ₁₂Δt + p3(t)λ₃₂Δt .

Переходя к дифференциальному уравнению, можно записать:

dp2/dt = λ₁₂p1 + λ₃₂p3 - (λ₂₁+λ₂₄)p2 . (2)

Получая по изложенной методике уравнения для состояний S3 и S4 и присоединяя к ним уравнения (1) и (2), можно записать системы дифференциальных уравнений для вероятностей состояний:

dp1/dt = λ₂₁p2 - (λ₁₂+λ₁₃)p1

dp2/dt = λ₁₂p1 + λ₃₂p3 - (λ₂₁+λ₂₄)p2

dp3/dt = λ₁₂p1 + λ₄₃p4 – λ₃₂p3

dp4/dt = λ₂₄p2 – λ₄₃p4

Эти уравнения называются уравнениями Колмогорова. Это система четырех линейных дифференциальных уравнений с четырьмя неизвестными функциями р1, р2, р3, р4. Начальные условия задаются в зависимости от того, каково было начальное состояние системы S. Например, если в начальный момент времени (при t=0) система была в состоянии Si, то pi(0) = 1, а все остальные вероятности равны нулю. Так, например, данную систему уравнений можно решать при начальных условиях: р1(0)=1, р2(0)=р3(0)=р4(0)=0.

Нужно отметить, что все четыре уравнения системы можно не записывать, так как можно воспользоваться условием р1+р2+р3+р4 = 1. Поэтому любую из вероятностей можно выразить через остальные и получить систему трех уравнений.

Анализируя систему уравнений, можно вывести общее правило формирования таких уравнений непосредственно по размеченному графу состояний, пригодное для любой непрерывной марковской цепи. В левой части каждого уравнения находится производная вероятности состояния, а правая часть содержит столько слагаемых, сколько стрелок связано с данным состоянием. Если стрелка направлена из состояния, соответствующее слагаемое имеет знак «минус», если в состояние – «плюс». Каждое слагаемое равно произведению плотности вероятности перехода, соответствующей данной стрелке, умноженной на вероятность того состояния, из которого исходит стрелка.