Лекция Моделирование физических процессов

Вид материала

Лекция

Содержание 2.2.Моделирование свободного падения тела. 2.3.Модель движения тела, брошенного под углом к горизонту. 2. Бросание тела вверх с начальной скоростью u0: h=0; A=90; u0>0; k=0; g=9,8 м/с 3 2.4. Уравнения матфизики 2.5.Классификация уравнений матфизики 2.6. Моделирование процесса теплопроводности Процесс теплопроводности

Подобный материал:

• Программа-минимум кандидатского экзамена по специальности 05. 13. 18 «Математическое, 93.92kb.
• Курс по выбору для предпрофильной подготовки «Моделирование физических процессов, 361.21kb.
• Обствует лучшему пониманию физических явлений, вырабатывает навыки моделирования виртуальной, 47.93kb.
• Расписание гр. 3520 Четная Понедельник 11: 00-12: 20 Анализ и моделирование бизнес, 15.28kb.
• Тема Моделирование и классы моделей, 45.36kb.
• Моделирование и оптимизация систем с распределенными параметрами, 14.61kb.
• Правительстве Российской Федерации» (Финансовый университет) Кафедра «Математическое, 246.23kb.
• Лекция: Моделирование бизнес-процессов средствами bpwin (часть 2): Стоимостный анализ:, 302.68kb.
• Урок по теме: "Моделирование физических процессов", 131.04kb.
• Лекция Компьютерное моделирование в решении физических задач. Типы компьютерных задачных, 155.43kb.

Лекция 2. Моделирование физических процессов.

2.1. Детерминированные модели

Физика – это наука, в которой математическое моделирование является весьма важным методом исследования. Исторически так сложилось что моделирование начиналось именно с построения моделей физических процессов.

Наряду с традиционным делением физики на экспериментальную и теоретическую, сейчас выделяется третий фундаментальный раздел – вычислительная физика. При максимальном проникновении в физику математических методов, порой доходящем до фактического сращивания этих наук (есть такая известная дисциплина - уравнения математической физики), реальные возможности решения математических задач традиционными аналитическими методами очень ограниченны. Во-первых, реальные физические процессы только в первом, очень грубом приближении можно описать простыми линейными уравнениями реально же, как правило, приходится иметь дело с нелинейными и дифференциальными уравнениями, во-вторых, при моделировании физических процессов необходимо учитывать совместное движение или влияние друг на друга многих тел, что приводит к необходимости решения систем уравнений высокого порядка (N=100). Такие задачи эффективнее не решаются не аналитическими методами, а численными методами, т.е. используется аппарат не чистой математики, скажем алгебры, а аппарат вычислительной математики.

При построении моделей используются два принципа: дедукции (от общего к частному) и индукции (от частного к общему). В зависимости от способа построения различают дедуктивные или детерминированные и индуктивные (недетерминированные) модели. Построение детерминированных моделей основано на использовании фундаментальных законов – именно такие модели строятся при моделировании физических процессов, если же фундаментальные законы, управляющие моделируемым явлением неизвестны, как это часто бывает при моделировании в биологии, социологии, экономике – то используются гипотезы.

Рассмотрим две простые детерминированные модели, модели двух простых физических явлений.

2.2.Моделирование свободного падения тела.

Примем, что тело массой m падает с высоты h с начальной скоростью V₀.

На тело действует сила тяжести F=mg, направленная вниз и сила сопротивления среды F_c= k₁v+k₂v² .Падение тела описывается 2 законом Ньютона:

ma=mg-F_c

в одномерной системе координат с осью х, направленной вниз, и с началом в точке начального падения тела.

Сила сопротивления среды F_c= k₁v+k₂v² зависит от скорости тела и его сечения,

k₁ – коэффициент Стокса, зависит от вязкости среды, большая величина;

k₂ – коэффициент лобового сопротивления, зависит от площади сечения тела, маленькая величина.

Если скорость не очень большая, то доминирует линейная составляющая, квадратичной же составляющей можно пренебречь, при более высоких скоростях напротив, резко возрастает квадратичная составляющая, а линейной составляющей можно пренебречь.

Что подразумевается под моделированием движения какого-либо тела? Это означает, что в каждый момент времени t_i мы должны знать положение тела в пространстве или пройденный им путь x=x(t), его скорость v=v(t) и ускорение a=a(t), которые будут являться функциями от времени. В начальный момент времени

t₀=0, x₀=0, v₀=0, a₀=g

Для построения расчетной модели предположим, что в течение малого промежутка времени Δt=τ движение равноускоренно, тогда можно использовать известные законы прямолинейного равноускоренного движения.

x=x₀+v₀ τ +a τ ²/2

v=v₀+a τ

a=const

Теперь можно построить такой вычислительный процесс:

t₀=0, x₀=0, v₀=0, a₀=g

t₁=t₀+τ, x₁=x₀+v₀+a₀ τ ²/2 v₁=v₀+a₀τ a₁=(mg- k₁v₁-k₂v₁²)/2


и т.д., далее пошли итерации, в i момент времени

t_i=t₀+i τ, x_i=x_i-1+v _i-1+a _i-1 τ ²/2 v _i=v _i-1+a _i-1τ a _i=(mg- k₁v _i-k₂v _i²)/2


Процесс закончен, когда x_i=h

Осталось определить задачи исследования и соответственно определить параметры модели для этих целей.

Задача о безопасности парашютиста. Пусть парашютист прыгает с высоты h м. Определить необходимый радиус парашюта, другими словами, нам нужно подобрать коэффициент сопротивления k₂, при котором имеем безопасное приземление. Кстати, оценить скорость безопасного приземления можно из следующих соображений. С какой высоты прыжок человека на землю безопасен? С первого этажа даже ребенку не страшно, а со второго надо постараться удачно приземлиться. Значит, можно взять среднюю высоту между первым и вторым этажом, скажем, 3 метра. Тогда при свободном падении тела за время

t=√2h/g=0.8 сек

величина скорости приземления

V_p=g*t=10*0.8=8 (м/сек.)

Другими словами, скорость безопасного приземления - 8-10 м/с.


Таким образом, параметрами модели будут являться
h - высота, с которой падает тело;
V_н - начальная скорость падения, в частности, V_н=0;
m - масса тела;
g - ускорение свободного падения; - статические параметры модели
τ – шаг по времени,
k - коэффициент сопротивления. - динамические параметры для моделирования.

Быстрее всего протекает процесс без сопротивления (нижняя оценка), и наоборот, самый медленный процесс, когда ускорение равно нулю, т.е. движение установившееся и происходит с постоянной скоростью, например V_p.

В качестве теста зададим k=0, тогда расчеты должны совпадать с формулами закона равноускоренного движения при a=g.

Если k=mg, то практически мгновенно движение устанавливается (а=0) и тело либо зависает (V=0), либо медленно опускается с постоянной скоростью.

Подобное проверочное тестирование в случае удачи дает основания к уверенной работе с моделью. Теперь можно проводить эксперименты с моделью. Попытаемся подобрать k таким образом, чтобы скорость установления была близка к значению 10 м/с.

2.3.Модель движения тела, брошенного под углом к горизонту.

Тело бросают с высоты h под углом α к горизонту.

Модель движения тела, брошенного под углом к горизонту строиться аналогично предыдущей модели, только вектора скорости и ускорения необходимо будет разложить по двум осям и учитывать составляющие вектора скорости v по x и по y v_x v_y и вектора ускорения a по x и по y a_x a_y. Сила сопротивления будет направлена обратно движению, сила тяжести – по-прежнему вниз.

X: ma_x=-k₁v_x-k₂v_x²

Y: ma_y=-(mg-k₁v_y-k₂v_y2)

Начальные условия в этой модели

T₀=0 x₀=0, y₀=h, v_o^x=v₀cos α, v_o^y=v₀sin α, a_o^x=0, a_o^y=-g

Расчетные формулы:


x=x+v_x τ +a_x τ ²/2

y=y+v_y τ +a_y τ ²/2


v_x=v_x+a_x τ

v_y=v_y+a_y τ


a_x=-(k₁v_x- k₂v_x²/m

a_y=(mg-k₁v_y- k₂v_y²)/m


Условие окончания процесса y=0.


Параметры модели:

h - начальная высота бросания, в частности, h=0;

v₀ - начальная скорость бросания тела;

α - угол бросания;

m - масса тела;

k₁ - коэффициент сопротивления среды;

k₂ - коэффициент лобового сопротивления;

g - ускорение свободного падения;

τ – шаг по времени.

Можно ставить следующие задачи: задача о подводной охоте (под каким углом следует выстрелить охотнику, если акула находится от него на расстоянии l метров?), задача о теннисном шарике (какой должна быть высота крытого корта, если угол α, под которым теннесист отправляет шарик заключен в диапазоне от α₁ до α₂? Если начальная скорость теннисного шарика v₀ (которая зависит от силы ударов по нему) заключена в диапазоне от v₀¹ до v₀² ?)

Тесты могут быть следующие:

1. Свободное падение с высоты h:

h>0; A=-90; u₀=0; k=0; g=9,8 м/с

2. Бросание тела вверх с начальной скоростью u₀:

h=0; A=90; u₀>0; k=0; g=9,8 м/с

3. Движение под углом к горизонту без сопротивления:

h=0; A=45; u₀>0; k=0; g=9,8 м/с

и т.п.

2.4. Уравнения матфизики

Для более сложных физических явлений, таких как процессы колебания, волновые процессы, процессы теплопроводности не всегда удается построить такие простенькие модельки. Реально эти процессы описываются дифференциальными уравнениями 2 порядка, уравнениями в частных производных, называемых уравнениями матфизики.

Напомню, что дифференциальным уравнением называется уравнение, куда входит искомая функция со своими производными

F(x,y(x),y’(x),y’’(x)…y⁽ⁿ⁾(x))=0

Наивысший порядок производной, входящей в уравнение, называется порядком дифференциального уравнения. Решением дифура является не число, а функция, x называется независимой переменной. Если искомая функция является функцией одной переменной, то дифур-ие называется обыкновенным дифур-ием, если искомая функция является функцией нескольких переменных, то дифур-ие называется ур-ием в частных производных.

В
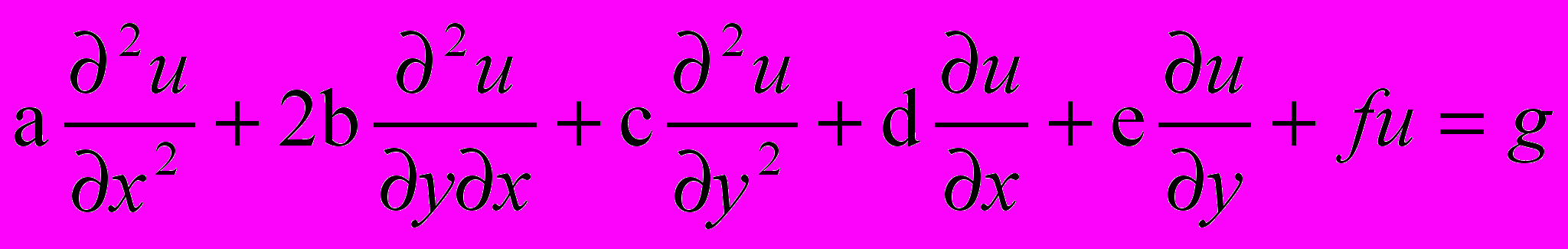
случае двух независимых переменных x и y ур-ия матфизики, которые являются как правило ур-иями первого и второго порядков, линейными относительно входящих в них производных можно записать в виде

Обычно одна из переменных – это время t

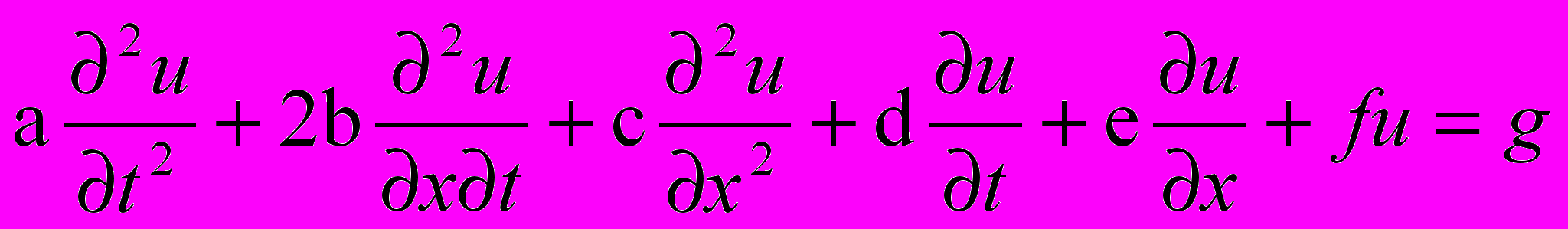
2.5.Классификация уравнений матфизики

Различают типы уравнений в зависимости от соотношения между коэффициентами.

1) При a=b=c=f=0, d≠0, e≠0 получаем уравнение первого порядка вида





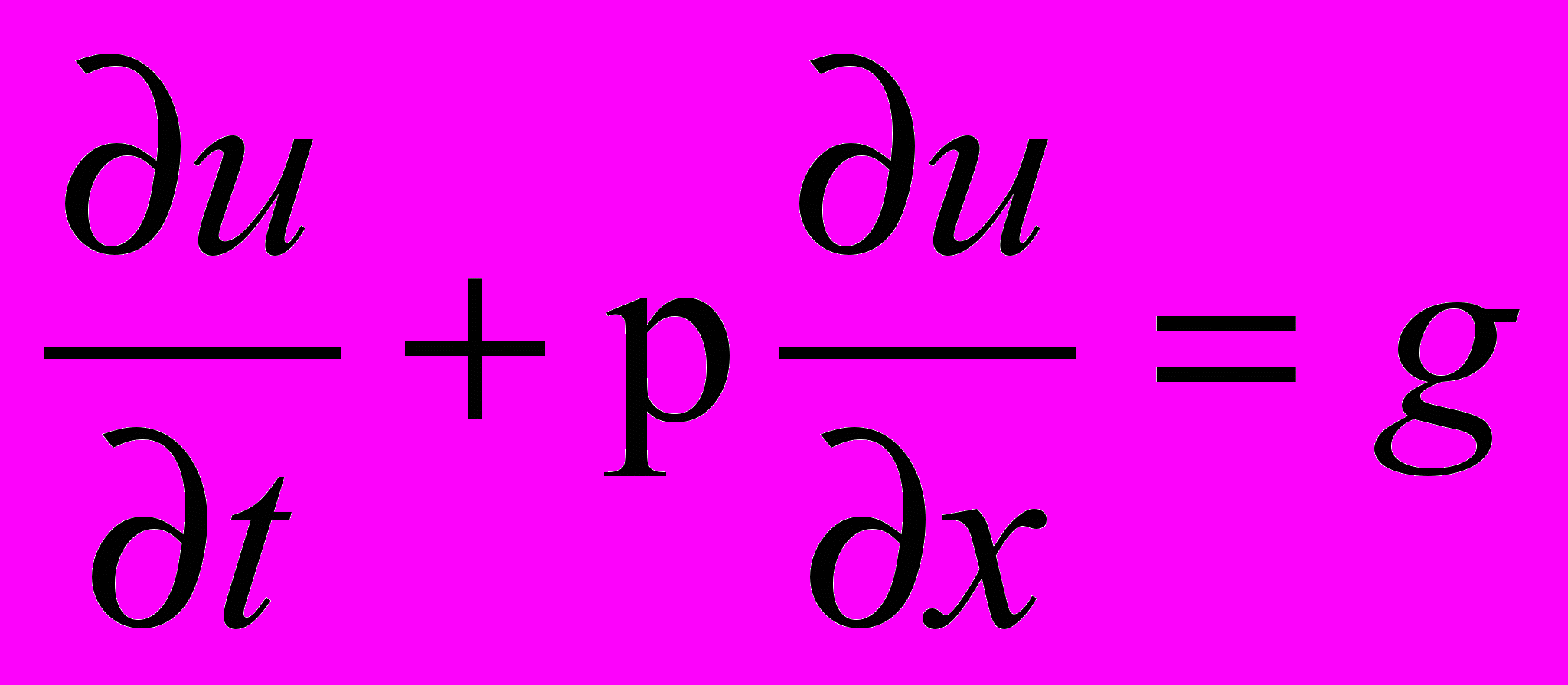
называемое уравнением переноса. Такие уравнения описывают процессы перенса частиц в различных средах, распространение возмущений и т.д. Искомая функция u=u(t,x) зависит от времени и от пространственной переменной, коэффициент p характеризует скорость переноса.

2) Если хотя бы один из коэффициентов a,b,c будет отличен от нуля, то уравнение будет иметь второй порядок и в зависимости от знака дискриминанта

D=b²-4ac

Будет принадлежать к одному из трех типов

D>0 – гиперболическое,

D=0 – параболическое,

D<0 – эллептическое.


А) Гиперболическое уравнение





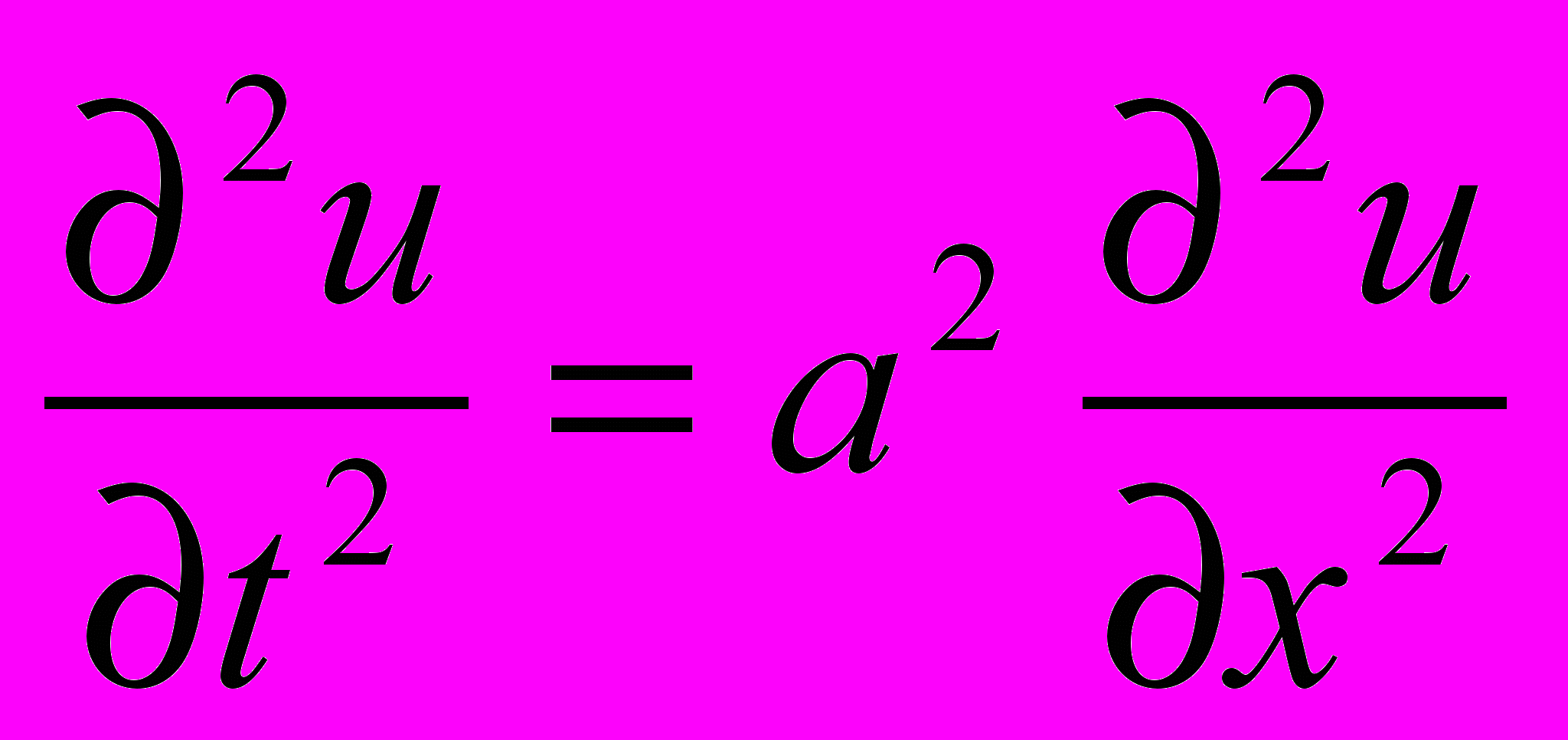
Называется волновым, оно описывает различные виды колебаний. Если в уравнение входит одна пространственная переменная, то оно описывает продольные колебания стержня, а также поперечные колебания струны. В этом случае a²=T/ρ, где T – это натяжение струны, а ρ – ее линейная плотность. Двухмерное волновое уравнение используется для описания колебаний тонкой пластины (мембраны)






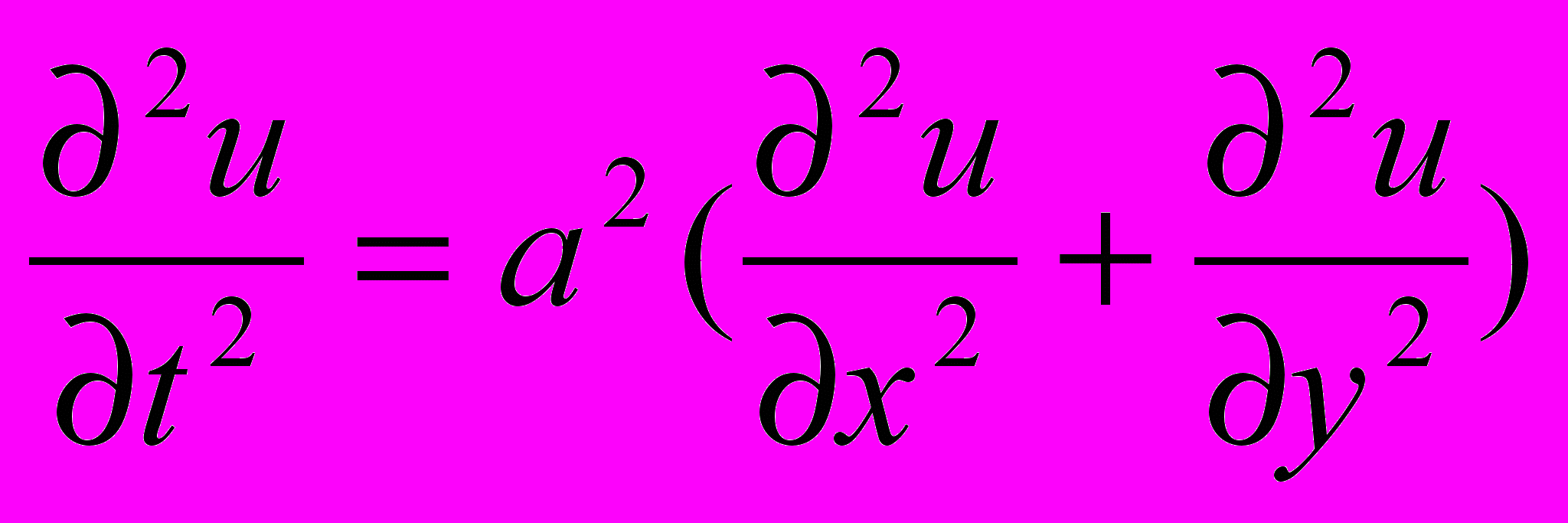
Трехмерное волновое уравнение





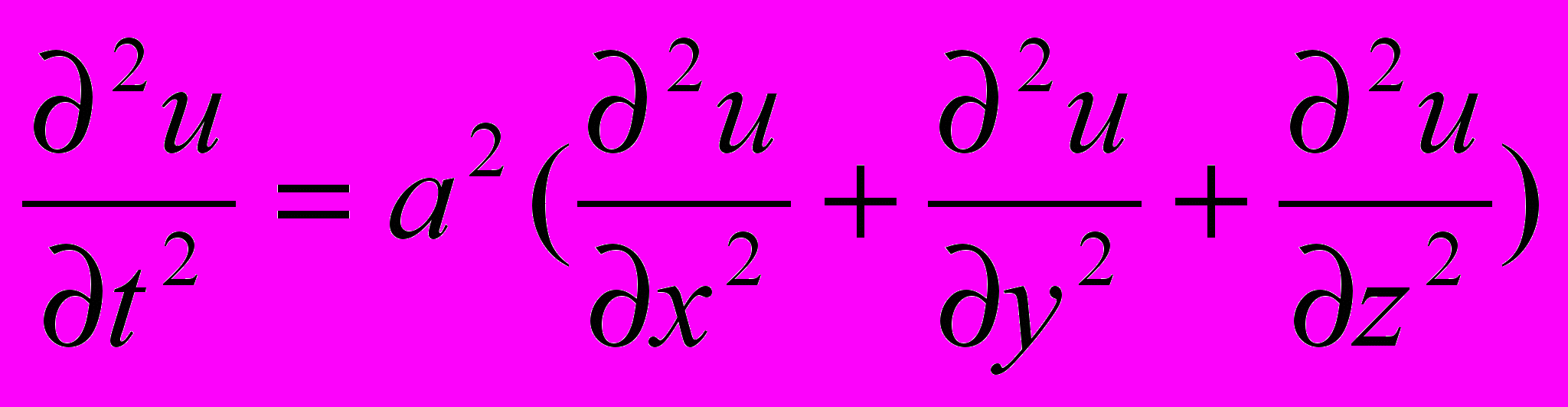
Описывает распространение волн в пространстве (например звуковые волны в различных средах, упругие волны в сплошной среде и т.д.)

б) параболическое уравнение





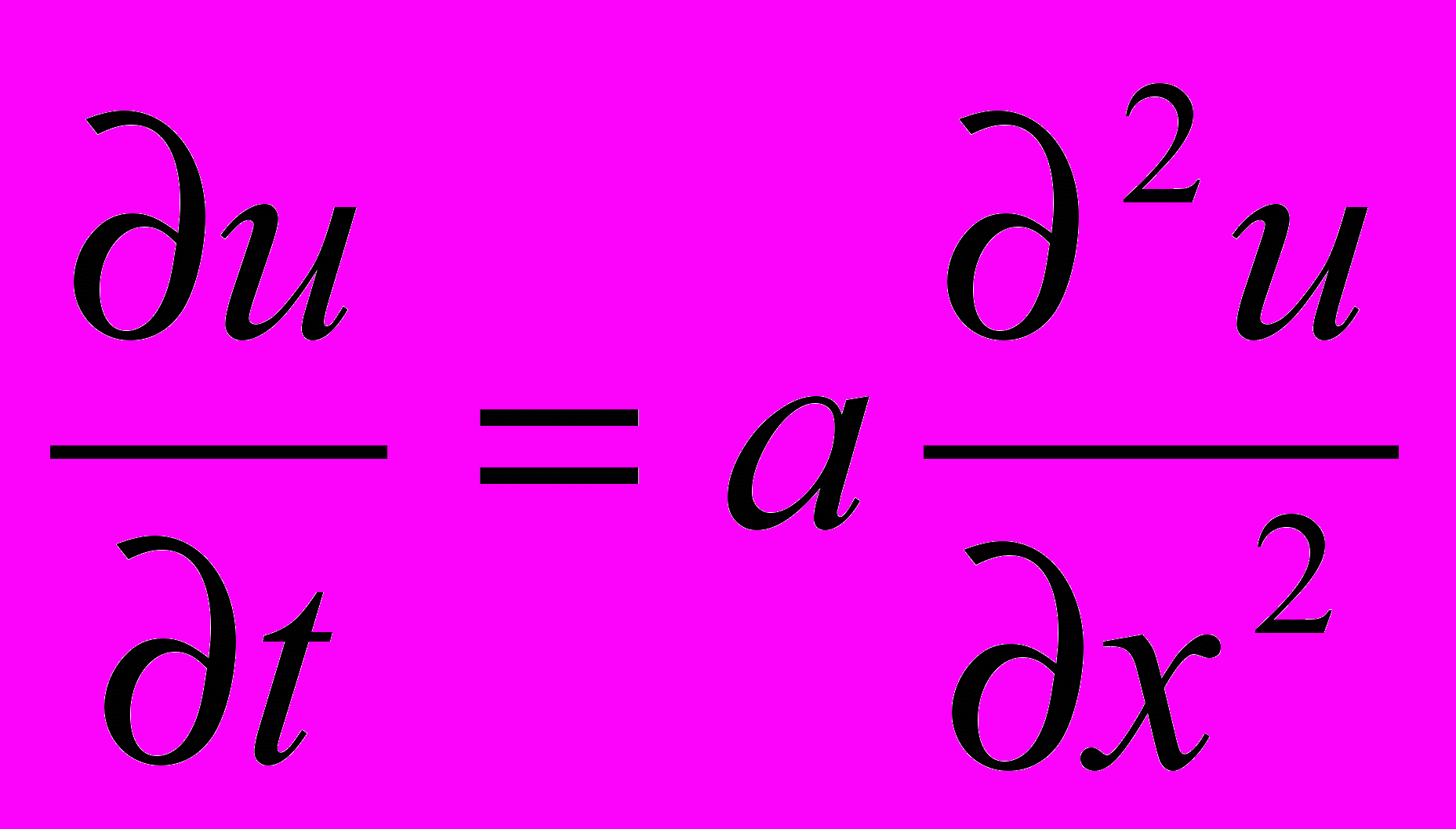
называется уравнением теплопроводности или диффузии с помощью него описываются различные процессы, связанные с передачей чего-либо: передачей тепла, передачей импульса, передача энергии.

В) Эллептическое уравнение





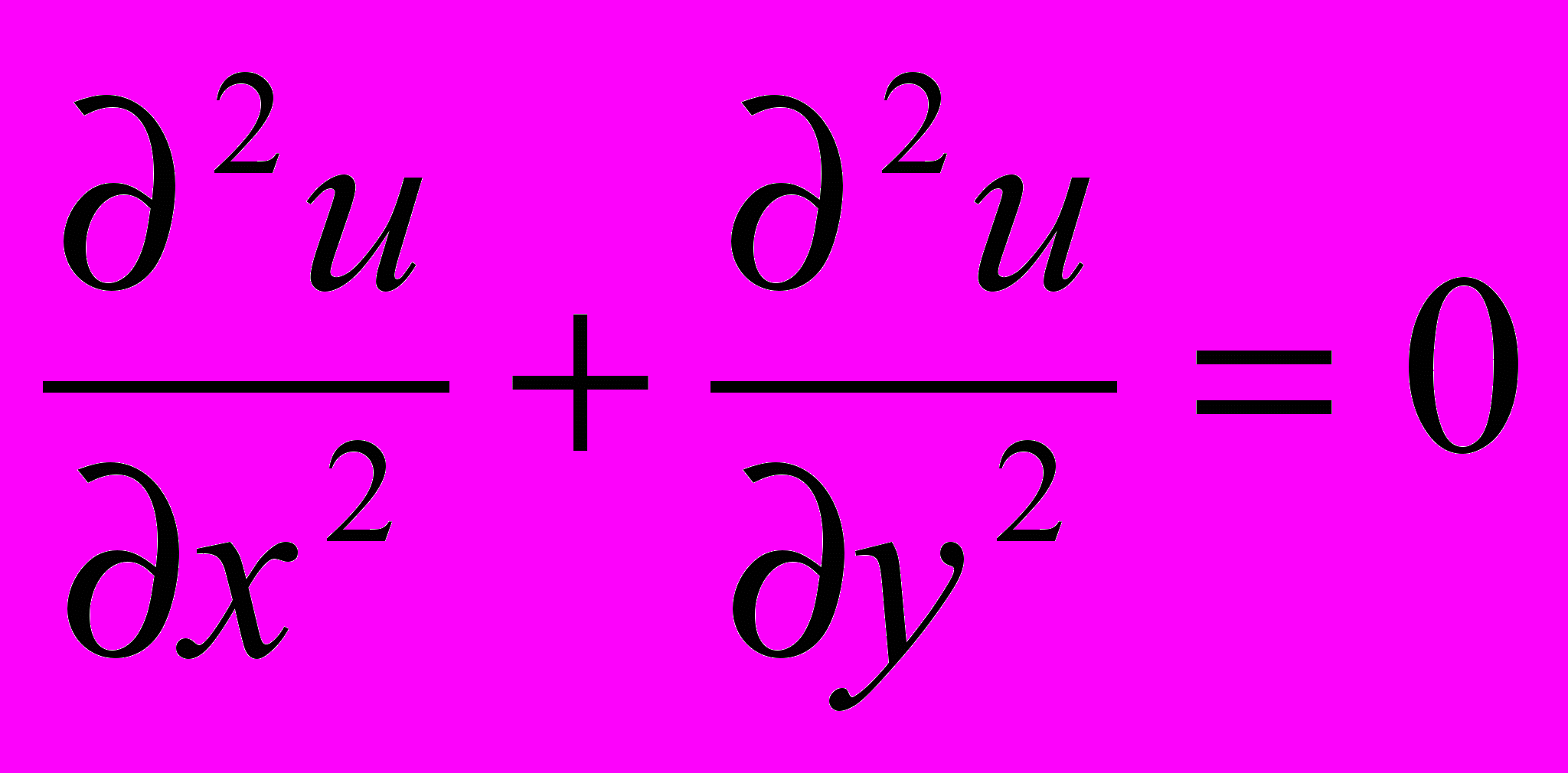
Уравнение Лапласа





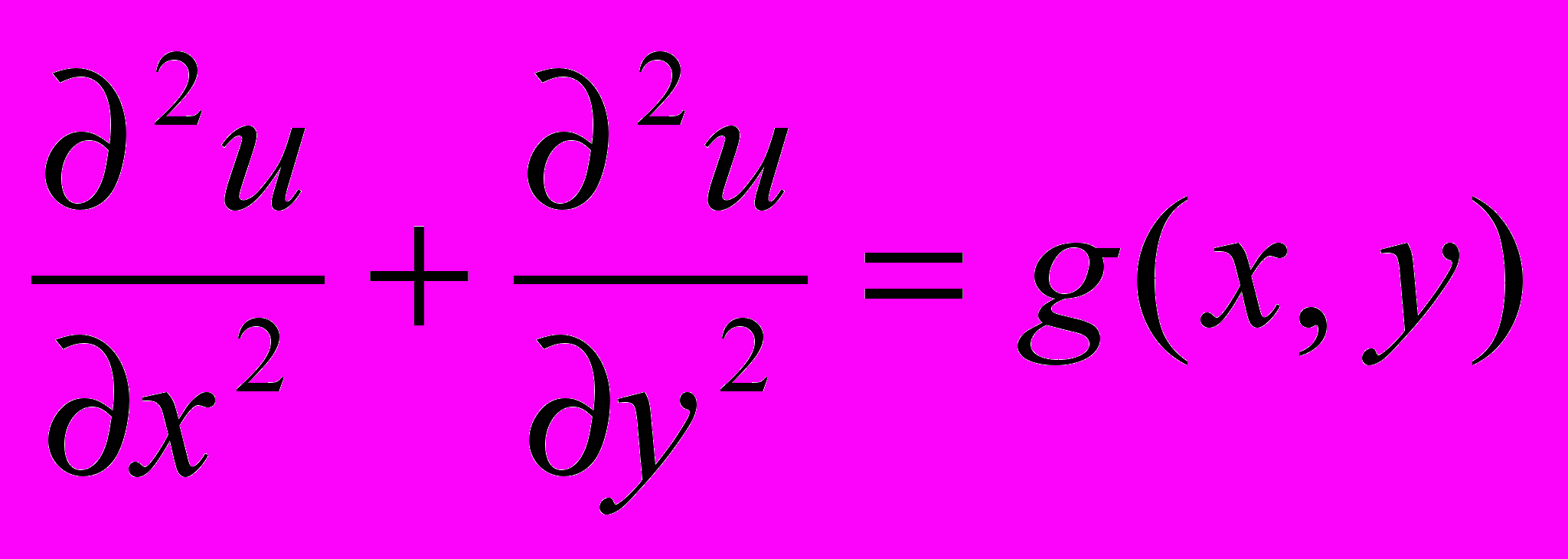
Уравнение Пуассона

К уравнениям такого типа приводят стационарные, не зависящие от времени, физические задачи (исследования потенциальных течений жидкости, определение формы нагруженной мембраны и т.д.)

2.6. Моделирование процесса теплопроводности

В качестве примера модели, в основе которой лежит уравнение матфизики рассмотрим модель распространения тепла в однородном стрежне. Задача теплопроводности.

Процесс теплопроводности возникает если тело неоднородно нагрето. Простейшая для изучения теплопроводности система — линейный однородный стержень. В простой модели боковая поверхность стержня считается теплоизолированной, т.е. через нее нет обмена теплом с окружающей средой.




Обозначим температуру стержня в точке с координатой х в момент времени t через u(x,t). Уравнение теплопроводности имеет вид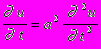





где а  коэффициент температуропроводности, зависящий в первую очередь от вещества, из которого сделан стержень.

Уравнение теплопроводности сопровождается начальными и краевыми условиями, делающими постановку задачи физически однозначной Напомню, что если для дифур-ия заданы начальные условия (условия в начальный момент времени), то такая задача называется задачей Коши, если же заданы краевые условия (на границах исследуемой области), то такая задача называется краевой задачей, если заданы и начальные и граничные условия, то мы имеем смешанную краевую задачу. Начальное условие задает распределение температуры в стержне в начальный момент времени (считаем его равным нулю):


u(x,0) = φ(x)


Краевые условия (их должно быть в данном случае два) указывают, в простейшем варианте, какая температура поддерживается на концах стержня:


u(0,t)=ψ₀(t), u(l,t)=ψ_l(t)


Заметим, что начальные и граничные условия должны быть согласованы, т.е.

u(0,0) = φ(0)=ψ₀(0)

u(l,0) = φ(l)=ψ_l(0)


Моделирование процесса теплопроводности связано с дискретизацией как временного изменения температуры, так и пространственного.

Введем равномерную прямоугольную сетку с помощью координатных линий

x_i=ih, i=0,1,….n,

t_j=jτ, j=0,1,….m,

где h – это шаг по пространству, по координате х, а τ – шаг по времени.

Значения функции в узлах сетки обозначим u_i^j=u(x_i,t_j).

Входящие в уравнение производные заменим их конечно-разностными аппроксимациями



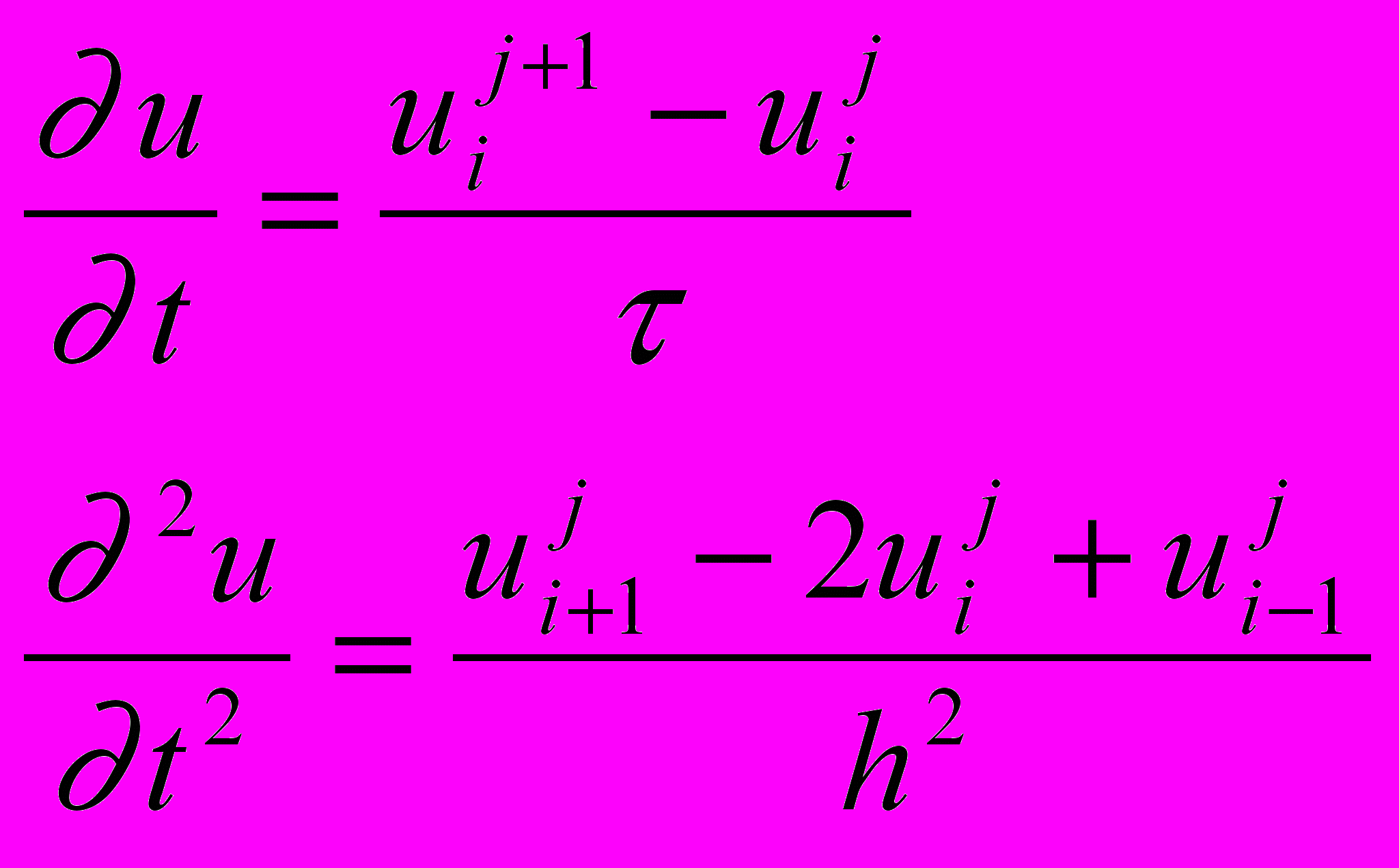
получим



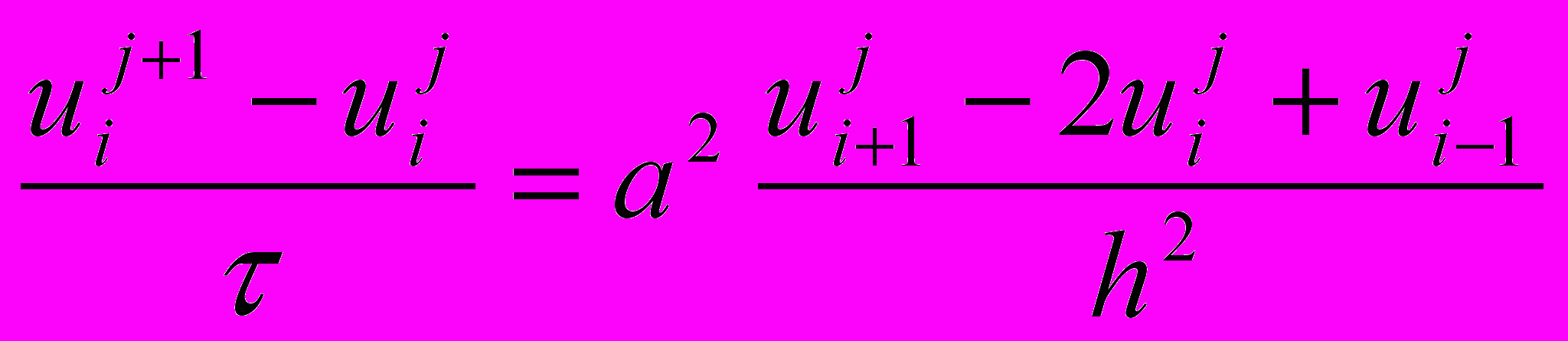
или

,

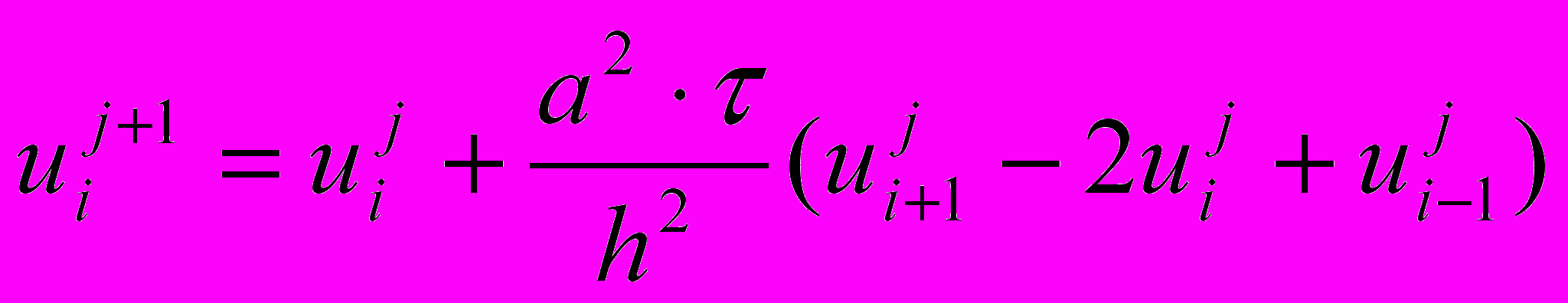где

i=0,1,….n,

j=0,1,….m,

Получилась явная разностная схема, удобная в применении, но устойчивая лишь при выполнении условия



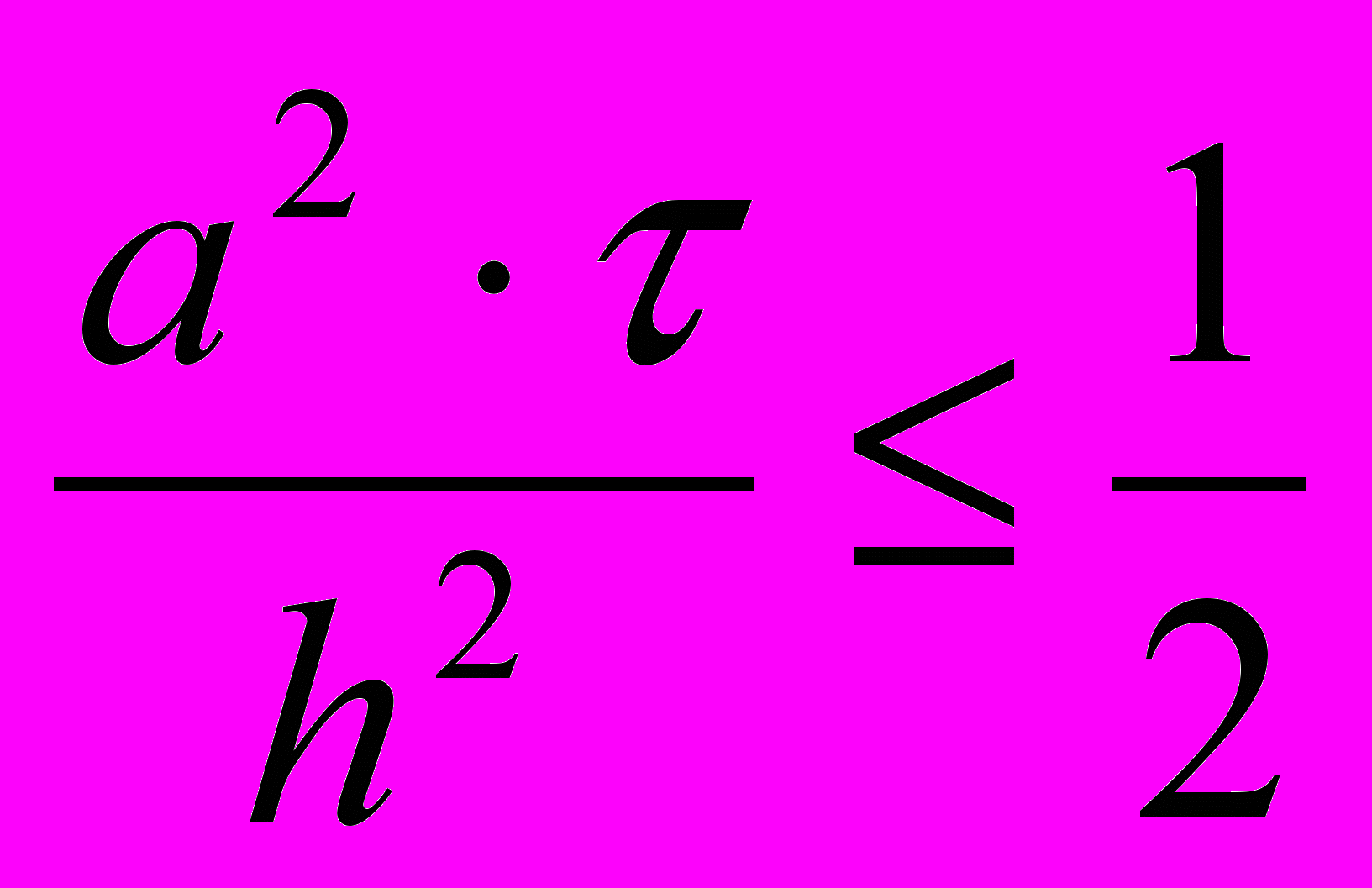
Это следует учитывать, выбирая шаги по времени и пространству.

Совокупность узлов в фиксированный момент времени называется слоем.

Построенная схема позволяет нам находить значение функции температур на j+1 слое через значения на j слое. Для начало счета приj=1 необходимо знать значения функции температур на нулевом слое. Они нам известны из начальных условий.

Если использовать другие конечно разностные соотношения для аппроксимации производных,





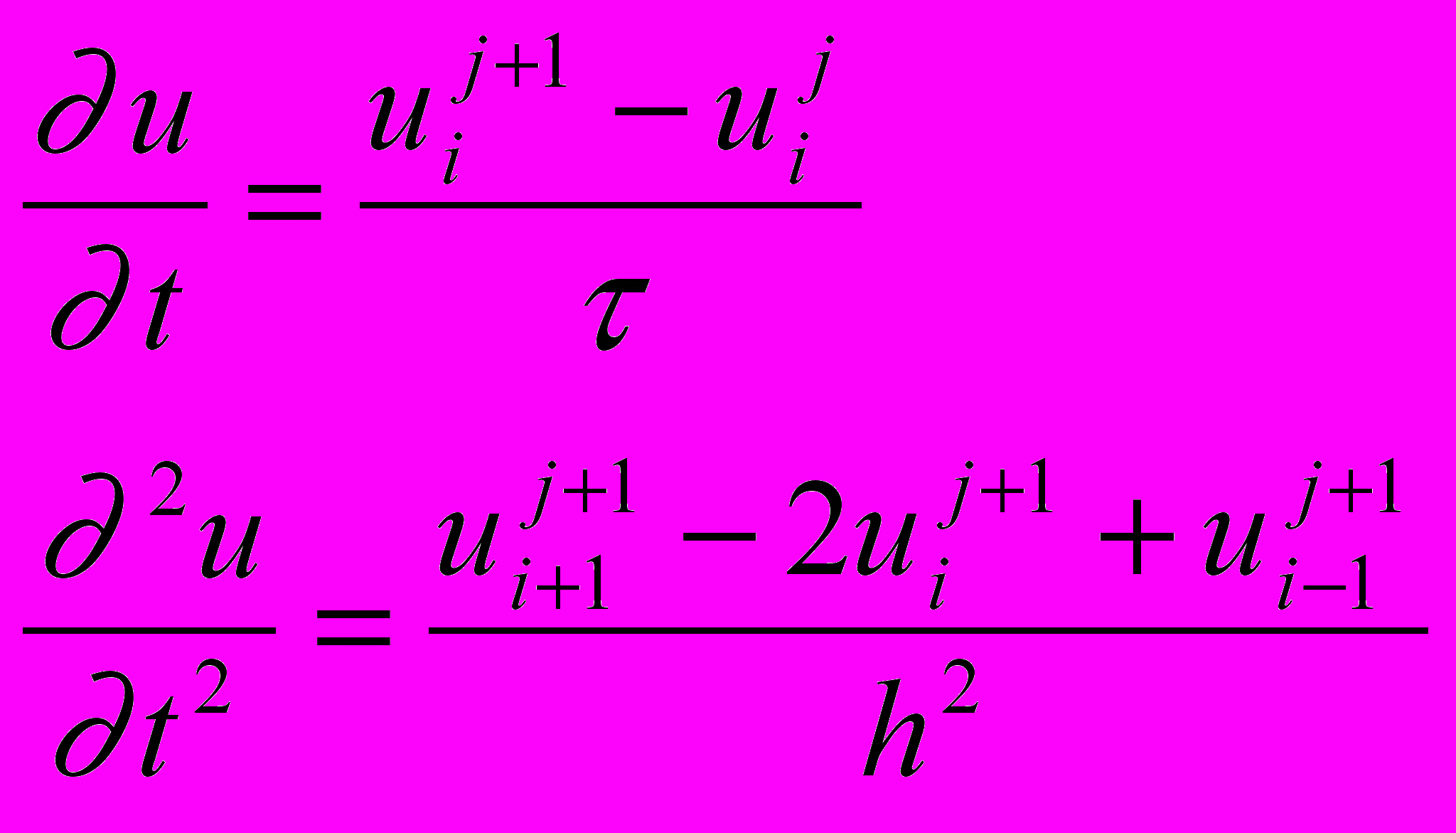
то получим существенно более устойчивую неявную схему




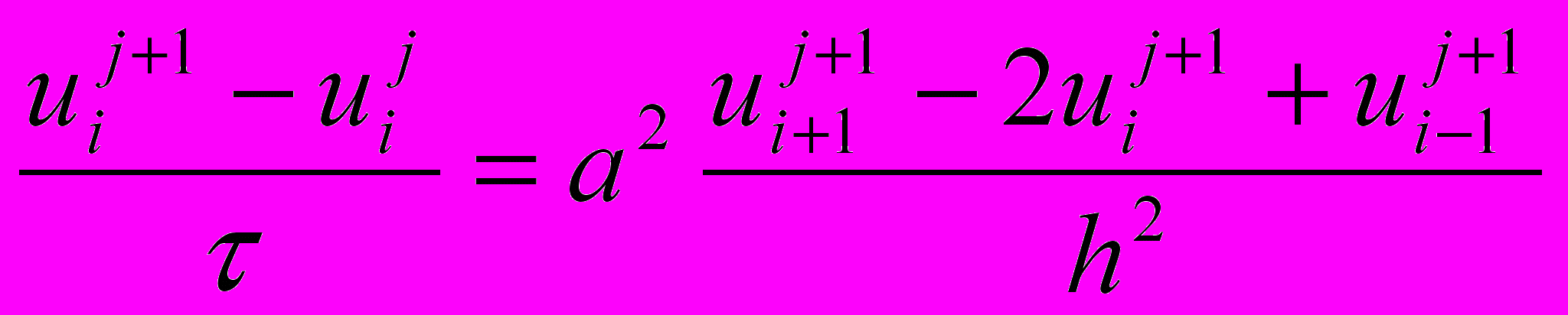
или




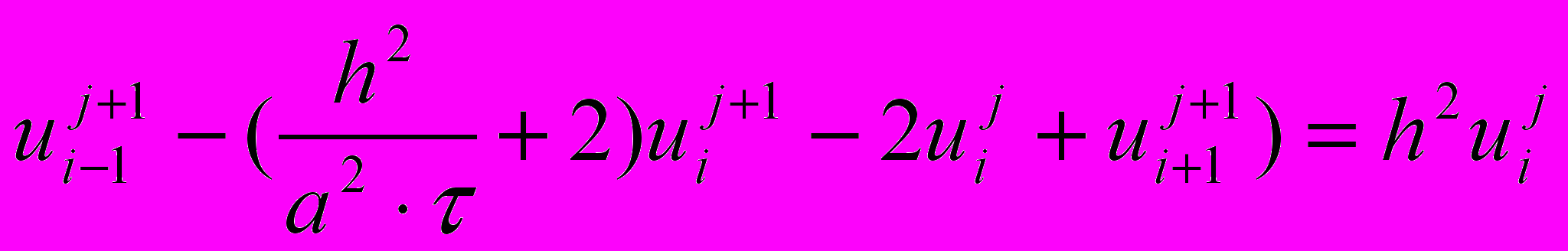
(В отличие от явной схемы каждое разностное уравнение второй схемы содержит на каждом новом слое три неизвестные значения, которые невозможно определить сразу же, как мы поступали в явной схеме. При этом вторая разностная схема состоит из линейных трех точечных уравнений, т.е. каждое уравнение содержит неизвестную функцию в трех точках нового слоя. Такие системы линейных уравнений, системы с трехдиагональной матрицей, могут быть легко решены методом прогонки. Таким образом, в случае неявной схемы, чтобы посчитать значения функции температур в каждый следующий момент времени, т.е., чтобы перейти на следующий слой по времени, необходимо каждый раз решать методом прогонки линейную систему. )

Это — система линейных алгебраических уравнений с трехдиагональной матрицей. Для ее решения наиболее эффективен метод прогонки.


Я попыталась продемонстрировать, как можно моделировать физические явления применяя математический аппарат во всей его мощи. Однако это довольно сложно. При моделировании явления теплопроводности можно пойти другим путем.

Пусть задана квадратная пластина, на краях которой известна температура. Требуется определить температуру во внутренних точках. Если предположить, что теплоотвода внутри нет, то можно смоделировать решение путем вычисления среднего значения T=(t1+t2+t3+t4)/4.

Однако это очень грубое приближение, ведь в разных точках пластины температура различна.

Разобьем квадрат на четыре части и для каждого малого квадратика применим ту же процедуру:

T11 = (t1 + T12 + T21 + t4)/4

T12 = (t1 + T11 + T22 + t2)/4

T21 = (t4 + T11 + T22 + t3)/4

T22 = (t2 + T21 + T12 + t3)/4

Или в другом виде

4T11 - T12 - T21 = t1 + t4

-T11 + 4T12 - T22 = t1 + t2

-T11 + 4T21 - T22 = t3 + t4

-T12 - T21 + 4T22 = t2 + t3

который представляет систему линейных уравнений относительно неизвестных T11, T