Моделирование

Вид материала

Документы

Содержание Вопрос №6. Обработка результатов моделирования. Оценка вероятности Оценка математического ожидания Оценка дисперсии. Колличество реализаций, обеспечивающих заданную точность

Подобный материал:

• Моделирование и формализация Моделирование как метод познания Моделирование, 143.04kb.
• Календарный план учебных занятий по дисциплине Моделирование информационных процессов, 24.12kb.
• Темы курсовых работ по дисциплине «моделирование систем» Ваш № в списке группы, 19.48kb.
• ИнтервальноЕ моделирование свойств сплава, 16.17kb.
• Программа спецкурса "Компьютерное моделирование нелинейных волновых процессов" Специальность, 27.11kb.
• Лекция Моделирование физических процессов, 111.71kb.
• Программа дисциплины имитационное моделирование в экономике для направления 080100., 228.47kb.
• Правительстве Российской Федерации» (Финансовый университет) Кафедра «Математическое, 246.23kb.
• Лекции по дисциплине «Социальное моделирование и программирование», 44.69kb.
• Учебно-методический комплекс по дисциплине "компьютерное моделирование" (факультет, 384.08kb.

Вопрос №6. Обработка результатов моделирования.

При изучении начального, нестационарного периода функционирования смо моделирование представляет, по существу, разыгрывание множества реализаций процесса, а нужные характеристики получаются обработкой эмпирических данных как статистическое среднее по множеству реализаций. При моделировании стационарных процессов можно воспользоваться одной, но достаточно длинной, реализацией, а интересующие характеристики рассчитать как среднее по времени.

Допустим, имеется 2х канальная СМО с очередью, максимальная длина которой три заявки. Если все три места в очереди заняты, то вновь поступившая заявка получит отказ и покинет систему. Поток заявок – пальмовский. Время обслуживания – случайная величина, распределенная по случайному закону.

Определим по одной, но достаточно длинной реализации следующие характеристики: вероятность занятости 0,1,2 каналов р0, р1, р2; вероятности того, что в очереди будет 0,1, 2, 3 заявки – (-р0), (-р1), (-р2), (-р3); среднее число занятых каналов – (-z); среднее время ожидания заявки в очереди – (-t_ож); среднее время обслуживания заявок - (-tоб); вероятность отказа р _отк.


Временная диаграмм а функционирования СМО изображена на рисунке. Вверху дана ось времени (0) с отмеченными моментами поступления заявок (t1-t14). На осях 1 и 2 показаны состоянии 1 и 2 канала соответственно. На осях 3-5 фиксируются состояния 1-3 мест в очереди соответственно.

Перед появлением первой заявки t1 все каналы и места в очереди свободны. В момент t1 поступает заявка и занимает первый канал. Время обслуживания τ1 формируется в результате работы генератора. В момент t2 прихода следующей заявки первый канал занят и она поступает на второй. Генерируется еще одно значение времени обслуживания τ2 . Заявка t3 приходит в систему, когда оба канала заняты, поступает в очередь и ждет освобождения одного из каналов. Раньше заканчивает обслуживание канал 2, заявка поступает в него и начинает обрабатываться. Далее процесс повторяется. Обработаем результат моделирования. В первую очередь найдем р0, р1, р2. Для этого разделим временную ось на участки и обозначим их цифрой 0 – если не занят ни один канал, 1- если занят один и 2 – если заняты оба канала.

Выберем большой участок времени моделирования (желательно, не с самого начала процесса, где сказывается влияние начальных условий) Т, на котором просуммируем длины участков, помеченных нолем, единицей и двойкой. Очевидно, что Т₀+Т₁+Т₂=Т.

Тогда р0≈Т0/Т; р1≈Т1/Т; …

Аналогично поступим для определения характеристик (-p0), (-p1), (-p2),(-p3).

(-р0)≈(-Т0)/Т; (-р1)≈(-Т1)/Т; …

Где (-Тi) – сумма длин участков, помеченных i-цифрой.

Среднее число занятых каналов (-z) определяется как (-z)=1p₁+2p₂

Среднее время ожидания заявки в очереди (-t_ож) опредя5еляется так: выберем большой участок Т и рассмотрим заявки, поступившие в моменты t_k,t_k+1, …, t_k+i …, для каждой из которых по эмпирическим данным подсчитаем время ожидания в очереди , равное нолю, если k+I заявка была сразу обслужена (или получила отказ), или сумме времен ожидания этой заявки на осях 3-5. Тогда




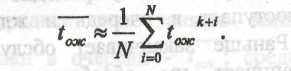
Среднее время обслуживания заявки по аналогии с (-tож) можно найти по формуле




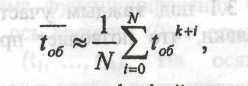
Вероятность отказа можно рассчитать по формуле




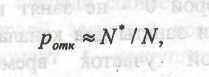
где N*- число заявок, получивших отказ; N – общее число заявок за время Т.


В процессе имитационного моделирования формируется большое количество реализации, являющихся исходным статистическим материалом для нахождения приближенных значений показателей эффективности или, как говорят, их оценок. В этих условиях обработка результатов моделирования может решаться только с применением методов, оптимальных по времени и обеспечивающих экономию памяти ЭВМ.

Перечислим ряд таких приемов.

Оценка вероятности

Оценкой вероятности является частота 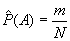. Для ее получения обычно организует на программном уровне 2 счетчика: один для подсчета общего количества экспериментов N, второй - для подсчета общего количества положительных исходов m.

Гистограммы. Иногда в качестве характеристик исследуемой системы выступает закон плотности распределения. Его приближенно можно охарактеризовать гистограммой. Для этого интервал изменения СВ разбивают на отрезки t i, каждому из них сопоставляют счетчик, где накапливают mi - количество попаданий значений СВ в t i. На каждом t i строится прямоугольник с высотой 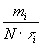Полученную гистограмму можно сгладить.

Оценка математического ожидания

Оценку математического ожидания получают как среднее арифметическое значение СВ



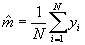
Сумму лучше всего вычислять (во избежание непроизводительных затрат памяти) путем постепенного накапливания.

Оценка дисперсии.


Оценку дисперсии можно вычислять по формуле 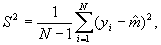однако это связано с непроизводительным использованием памяти ЭВМ. Поэтому лучше воспользоваться формулой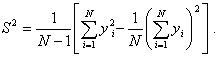

Оценка корреляционного момента.

Из тех же что в 2.6.4. соображений для оценки корреляционного момента двух случайных величин 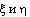рекомендуется использовать формулу



Для вычисления оценки характеристик СП производят статистическую обработку по N реализациямит СП. Для этого интервал задания СП разбивают на части с 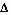t=const. Матожидания и дисперсии для каждого tk=k 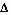t можно вычислить по формулам, приведенным выше. Оценку корреляционной функции - по формуле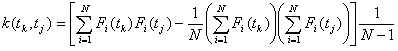

Колличество реализаций, обеспечивающих заданную точность.

Важной задачей обработки информации является задача определения количества реализаций N, обеспечивающих заданную точность получения оценок. Для определения N при оценке вероятности b пользуются формулой

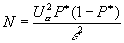
а при оценке матожидания -

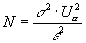
В формулах Ua- квантиль, для нормального, центрированного нормального закона распределения, соответствующий значению 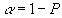где P заданная достоверность; P* - оцениваемая вероятность; 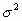дисперсия; 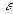допустимая погрешность. В этих формулах - 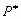неизвестно, а 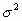может быть неизвестным. Поэтому производят предварительно 50-100 реализаций, получают по ним оценк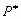и и 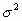подставляют их в формулы для вычисления уточненного значения N.