Моделирование
| Вид материала | Документы |
- Моделирование и формализация Моделирование как метод познания Моделирование, 143.04kb.
- Календарный план учебных занятий по дисциплине Моделирование информационных процессов, 24.12kb.
- Темы курсовых работ по дисциплине «моделирование систем» Ваш № в списке группы, 19.48kb.
- ИнтервальноЕ моделирование свойств сплава, 16.17kb.
- Программа спецкурса "Компьютерное моделирование нелинейных волновых процессов" Специальность, 27.11kb.
- Лекция Моделирование физических процессов, 111.71kb.
- Программа дисциплины имитационное моделирование в экономике для направления 080100., 228.47kb.
- Правительстве Российской Федерации» (Финансовый университет) Кафедра «Математическое, 246.23kb.
- Лекции по дисциплине «Социальное моделирование и программирование», 44.69kb.
- Учебно-методический комплекс по дисциплине "компьютерное моделирование" (факультет, 384.08kb.
Вопрос №3,4. Имитационная модель одноканальной СМО.
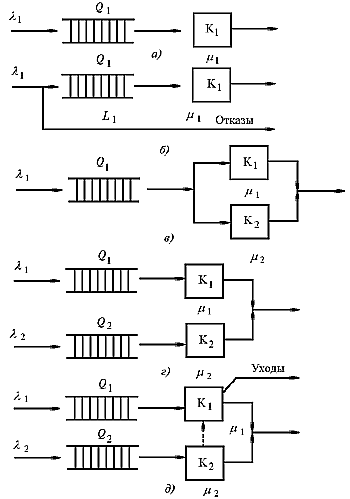
Рис. 3.1. Системы массового обслуживания:
а, б – одноканальные;
в, г, д – двухканальные
В
зависимости от характера источника заявок различают разомкнутые и замкнутые СМО. На рис. 3.1 представлены только разомкнутые СМО. В зависимости от числа мест в очереди различают СМО с отказами и без отказов. В СМО с отказами число мест в очереди конечно и вследствие вероятностного характера как входящего потока, так и процессов обслуживания существует ненулевая вероятность того, что поступившая на вход СМО заявка застанет все каналы занятыми обслуживанием и все места в очереди занятыми ожидающими обслуживания заявками, т. е. она получит отказ. В СМО без отказов заявка либо сразу назначается на обслуживание, если в момент ее поступления свободен хотя бы один канал, либо безусловно принимается в очередь.Кратко рассмотрим методику составления сетевых моделей на примере одноканальной СМО (в совокупности с генератором заявок). Следует отметить, что процесс разработки сетевых моделей в общем случае является неформализованным. Проинтерпретируем СМО в терминах транзакций и ресурсов. Транзакции – это активные подвижные элементы системы, а ресурсы – неактивные. Транзакциями в СМО являются заявки, а ресурсом является канал обслуживания заявок. Функционирование СМО описывается как взаимодействие транзакций и ресурсов.
Рис. 3.1. Системы массового обслуживания:
а, б – одноканальные;
в, г, д – двухканальные
При переходе от системы транзакций и ресурсов к сетевой модели можно пользоваться следующими правилами. Каждый ресурс представляется позицией, причем маркировка этой позиции (простыми метками) определяет состояние ресурса. В одноканальной СМО имеется один ресурс, имеющий два состояния: "занят" и "свободен", причем начальное состояние ресурса – "свободен". Поставим этому ресурсу в соответствие позицию R сетевой модели. Маркировка М(R) = 1 будет свидетельствовать о незанятости ресурса, а М(R) = 0 – о его занятости. Маркировка M(R) >=2 является запрещенной. Переход ресурса из одного состояния в другое представляется изменением маркировки позиции R: добавление метки соответствует освобождению ресурса, а изъятие – его занятию.
В системе транзакций и ресурсов каждая транзакция представляется простой меткой или меткой с атрибутами в зависимости от того, несет она информацию или нет. Будем считать, что в нашей одноканальной СМО каждая транзакция несет информацию и, следовательно, будет представляться меткой с атрибутами.
Транзакция в процессе ее обработки может находиться в нескольких состояниях, определяющих степень ее готовности. Для одноканальной СМО можно выделить следующие состояния транзакции:
0 – "готова для планирования";
1 – "планируется";
2 – "ожидание обслуживания";
3 – "заняла канал обслуживания";
4 – "обрабатывается";
5 – "обработана";
6 – "покинула канал обслуживания".
Состояния транзакции можно разделить на следующие классы:
– состояния временной активности (1, 4), связанные с процессами обработки транзакции, а также с планированием транзакции в генераторе транзакций. В этих состояниях транзакция находится во временной задержке перехода;
– состояния ожидания какого-либо ресурса (2). В этих состояниях транзакция находится в позициях, в которых нередко образуются очереди;
– состояния без ожидания (0, 3, 5, 6). В этих состояниях транзакция только "заявляет" о необходимости выполнения какого-либо события.
Каждому состоянию транзакции поставим в соответствие позицию или временную задержку перехода сетевой модели.
Переход транзакции из одного состояния в другое представляется как перемещение метки из одной позиции в другую, из позиции во временную задержку перехода, а также из временной задержки перехода в позицию.
В дальнейшем в моделируемой системе определяется множество событий, которые приводят к изменению состояния транзакций и ресурсов. В одноканальной СМО с генерацией заявок можно выделить следующие события:
1. "Приход новой заявки". При возникновении этого события транзакция переходит из состояния 1 в состояние 2. Создается копия транзакции, которая переводится в состояние 0.
2. "Планирование следующей заявки". Транзакция из состо-яния 0 переходит в состояние 1.
3. "Занятие канала обслуживания". Транзакция из состояния 2 переходит в состояние 3, а ресурс из состояния "свободен" переходит в состояние "занят".
4. "Начало обработки заявки". Транзакция из состояния 3 переводится в состояние 4.
5. "Конец обработки заявки". Транзакция из состояния 4 переводится в состояние 5.
6. "Освобождение канала обслуживания". Транзакция из состояния 5 переходит в состояние 6, а ресурс из состояния "занят" переходит в состояние "свободен".
7. "Уничтожение заявки". Транзакция покидает состояние 6 и уничтожается.
Каждому событию ставится в соответствие переход или пост-переход сетевой модели:
событие 1 – постпереход ТG;
событие 2 – переход TG;
событие 3 – переход SEIZE (мгновенный);
событие 4 – переход ADVANCE;
событие 5 – постпереход ADVANCE;
событие 6 – переход RELEASE (мгновенный);
событие 7 – переход TERMINATE (мгновенный).
На основе анализа причинно-следственных связей моделируемой системы производится соединение выделенных позиций и переходов с помощью дуг. При этом входные позиции какого-либо перехода будут определять необходимые условия возникновения соответствующего события, а выходные позиции – условия, которые возникают в результате совершения соответствующего события. Если событие приводит к модификации параметров транзакции, ее временной задержке или выбору последующего состояния в зависимости от определенных условий, то с переходом сетевой модели связывается процедура, производящая соответствующие действия. Следует отметить, что приведенный выше вариант "выделения" состояний и событий является не единственным. В результате отмеченных выше действий была получена сетевая модель,представленная на рис. 3.2,а. Следует заметить, что через переход TG имеется два потока меток: (PG, PG) и (PG, QUEUE). Графически это отображается следующим образом: позиция PG соединяется с одним из контактов перехода TG. Этот же контакт перехода соединяется с позициями PG и QUEUE.
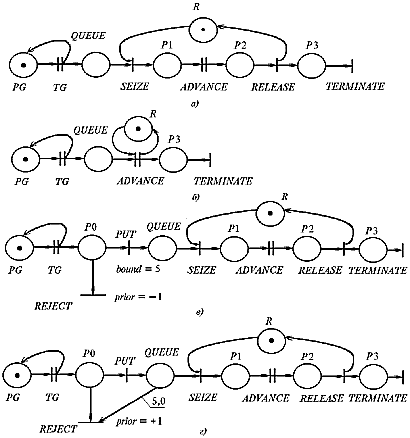
Рис. 3.2. Сетевые модели разомкнутых одноканальных СМО:
а, б – СМО без отказов;
в, г – СМО с отказами
Н
а рис. 3.2,б представлена сетевая модель одноканальной СМО, построенная на основе второго варианта "выделения" состояний и событий. Сеть на рис. 3.2,б эквивалентна предыдущей рассмотренной сетевой модели. Особенностью второго варианта является совмещение нескольких состояний и нескольких событий первого варианта. Целесообразно производить объединение тех событий, которые при обработке транзакции непосредственно следуют одно за другим, не разделены временным промежутком и когда условие возникновения второго события целиком зависит от первого.Срабатывание перехода ADVANCE сетевой модели второго варианта интерпретируется как событие "занятие канала обслуживания и начало обработки заявки", что соответствует двум событиям (3 и 4) первого варианта. Срабатывание постперехода ADVANCE сетевой модели второго варианта интерпретируется как событие "Конец обработки заявки и освобождение канала обслуживания", что соответствует двум событиям (5 и 6) первого варианта.
Нахождение транзакции во временной задержке перехода ADVANCE сетевой модели второго варианта интерпретируется как состояние транзакции "Заняла канал обслуживания и обрабаты-вается", что соответствует двум состояниям (3 и 4) транзакции в первом варианте. Нахождение транзакции в позиции Р3 интер-претируется как состояние транзакции "Обработана и покинула канал обслуживания", что соответствует двум состояниям (5 и 6) транзакции в первом варианте.
MODEL CMO1 ( );
PLACE PG:MARK=1/1 DATA;
QUEUE,P1,P2,P3:DATA;
R:MARK=1 SIMPLE;
TRAN TG, SEIZE, ADVANCE, RELEASE, TERMINATE;
LINK PG=>TG..=>(PG;QUEUE=>SEIZE=>P1=>ADVANCE..=>
P2=>RELEASE=>P3=>TERMINATE);
RELEASE=>R=>SEIZE
VAR IX1,IX2:INTEGER;
PROC FOR INITIAL:
IX1:=9; IX2:=5;
END;
PROC FOR TG:
DELAY:=RANDOM(72.0,132.0,IX1);
PG.1.P[1]:=RANDOM(50.0,150.0,IX2);
END;
PROC FOR ADVANCE:
DELAY:=P1.1.P[1];
END;
END CMO1;
Pис. 3.3. Модель одноканальной СМО
Текстовое представление сетевой модели (рис. 3.2,а) на языке ЯОСМ приведено на рис. 3.3. Позиции PG, QUEUE, P1, P2, P3 относятся к типу позиций, маркируемых метками с атрибутами. Транслятор автоматически определяет тип позиции по марки-ровке, производя трассировку путей движения меток с атрибута-ми по элементам сетевой модели. Трассировка начинается из источников меток с атрибутами, в качестве которых выступают позиции, начально помеченные метками с атрибутами, а также выходные контакты "оболочки" сетевого макроопределения, отмеченные описателями TDATA и PDATA. В рассматриваемой сетевой модели имеется единственный источник меток с атрибутами – это позиция PG, начально маркированная одной меткой с одним атрибутом. В результате трассировки сетевой модели оказывается, что метки с атрибутами не заходят в позицию R, поэтому данная позиция помечается как "маркируется простыми метками". Начальная маркировка позиции R – одна простая метка.
Cледует отметить, что позиция, маркируемая метками с атрибутами, не должна маркироваться простыми метками, и наоборот. В процессе разработки сложной модели бывает трудно отследить данные требования. Для контроля соответствия действительного типа позиции по маркировке желаемому были введены два контрольных описателя – DATA и SIMPLE (см. подразд. 2.5). Позиции PG, QUEUE, P1, P2, P3 отмечены описателем DATA, а позиция R – описателем SIMPLE. Если бы в результате трассировки сетевой модели действительный тип позиций из первого множества был определен как "маркированные простыми метками" или действительный тип позиции R был определен как "маркированная метками с атрибутами", то транслятор выдал бы диагностическое сообщение о несоответствии желаемого и действительного типа.
Временная задержка в переходе TG определена как имеющая равномерный закон распределения с математическим ожиданием 102 (единиц модельного времени). Величина задержки в переходе ADVANCE определяется процедурой этого перехода путем присвоения переменной DELAY значения атрибута P[1] метки, находящейся первой в позиции P1. Значение же первого атрибута метки определяется при генерации метки процедурой перехода TG. При этом атрибуту P[1] присваивается значение случайной величины, распределенной по равномерному закону с математическим ожиданием 100. Следует отметить, что временная задержка в переходе определяется не только путем описания перехода в TRAN-предложении или путем присваивания переменной DELAY значения в соответствующей переходу процедуре, но также использованием признака временной задержки ".." совместно с именем временного перехода при описании связей в LINK-предложении. Процедура перехода вводится конструкцией PROC FOR <имя перехода>.
При описании связей используется алгебра представления графов (АПГ). Структура сетевой модели (граф) определяется с использованием операций наложения ";" и соединения "=>" графов. По определению языка ЯОСМ граф есть последовательность цепочек, соединенных операциями наложения. У каждой цепочки выделяются головные вершины (головы) и хвостовые вершины (хвосты). В простейшем случае цепочка содержит одну вершину, которая является и головой, и хвостом. При наложении нескольких цепочек получается граф, у которого множество головных вершин образуется путем объединения головных вершин соответствующих цепочек, а множество хвостовых вершин получается путем объединения хвостовых вершин соответствующих цепочек. Описание графа заключается в круглые скобки (за исключением графа верхнего уровня, описание которого следует за ключевым словом LINK).
Каждая цепочка определяется как последовательность звеньев, соединенных операцией соединения "=>". Звеном может являться вершина, граф или FOR-свертка графа, о которой речь пойдет ниже. Вершина представляет собой или позицию, или контакт перехода, или контакт нетерминала, или контакт оболочки. В любом случае у звена выделяется множество головных и хвостовых вершин. Если звеном является вершина, то она является и головой, и хвостом данного звена. Операция соединения двух звеньев заключается в том, что каждая хвостовая вершина первого звена соединяется с каждой головной вершиной второго звена, причем сгенерированным дугам назначаются атрибуты дуги, описание которых может иметься как возле первого, так и возле второго звена.
При описании связей переход представляется множеством своих контактов. При определении структуры сетевой модели на языке ЯОСМ контакт перехода Т описывается как Т.К или Т..К, где К-числовой идентификатор контакта (ЧИК) (номер контакта). Вторая конструкция описывает контакт временного перехода. При описании связей ЧИК может быть опущен. В этом случае сам транслятор производит его назначение (получается внутренний ЧИК). Внутренний ЧИК недоступен для пользователя. У перехода может быть несколько контактов с различными внутренними ЧИК. Всякий раз, когда в описании связей имя перехода встречается без ЧИК, транслятор определяет новый контакт перехода и присваивает ему новый внутренний ЧИК. В приводимом ниже примере под TG подразумевается контакт перехода с внутренним ЧИК.
Рассмотрим описание связей сетевой модели, представленной на рисунке 3.2,а. Обозначим структуру данной модели через G1. Граф G1 представляется одной цепочкой вида: PG => TG.. => Z, где звенья PG и TG.. являются вершинами – позицией и контактом перехода соответственно; звено Z представляет граф G2, Z = (G2). Граф G2 можно представить в виде наложения двух цепочек: G2 = PG; C, где цепочка PG является вершиной, а именно – позицией, а С представляет цепочку:
QUEUE => SEIZE => P1 => => ADVANCE.. => P2 => =>RELEASE => P3 => TERMINATE.
Граф G2 имеет две головные вершины: PG и QUEUE. Следовательно, при соединении контакта перехода TG.. с графом G2 (обозначается как TG..=>(G2)) появляются дуги
Описание атрибутов дуг заключается в угловые скобки. Синтаксис и семантика атрибутов, описывающих дугу, зависят от ее типа: входная или выходная, групповая или одиночная, ингибиторная или числовая.
Более полные сведения об атрибутах дуг можно получить из приложения 3 с описанием синтаксиса ЯОСМ (правила 62–68). Если описание атрибутов дуги не задано явно, то по умолчанию входной дуге перехода присваивается описатель <,1,1> (эквивалентен описателю <1,1>), а выходной – <,FIFO,1> (эквивалентен описателю
Первый пустой компонент первого описателя свидетельствует, что дуга числовая одиночная; второй компонент определяет разметку активизации дуги, равную 1 (т. е. число меток в позиции – источнике дуги, необходимое для разрешенности соответствующего перехода, должно быть не меньше единицы); третий компонент определяет, что при срабатывании перехода из соответствующей позиции будет удалена одна метка.
Первый пустой компонент второго описателя свидетельствует, что дуга одиночная; второй компонент указывает, что метки с атрибутами будут включаться в выходную позицию-очередь в соответствии с дисциплиной FIFO; третий компонент указывает, что в выходную позицию при срабатывании перехода будет добавлена одна метка.
При явном описании атрибутов дуги описатель может стоять справа от вершины-источника или слева от вершины-приемника. В приведенном ниже примере все фрагменты, описывающие одну и ту же дугу, эквивалентны:
...QUEUE => SEIZE...
...QUEUE<,1,1> => SEIZE...
...QUEUE<1,1> => SEIZE...
...QUEUE => <,1,1>SEIZE...
...QUEUE => <1,1>SEIZE...
...QUEUE<,1,1> => <,1,1>SEIZE...
...QUEUE<1,1> => <1,1>SEIZE...
Если одной и той же дуге приписываются два описателя, то транслятор производит проверку их непротиворечивости. Если описатели противоречат друг другу, то выдается диагностическое сообщение.
При описании связей допускается многовариантность. Самым простым способом является описание структуры сетевой модели в виде списка бинарных связей. Однако рекомендуется описывать структуру в виде осмысленных фрагментов. Например, если обработка транзакции носит последовательный характер, то целесообразно представить технологический цикл ее обработки в виде цепочки элементов сетевой модели. В случае одноканальной СМО эта цепочка имеет вид:
QUEUE => SEIZE => P1 => ADVANCE.. => P2 => RELEASE => => P3=> TERMINATE.
В общем случае в структуре сетевой модели рекомендуется выделять графы продвижения транзакций каждого класса и отдельно их описывать. Ресурсные цепи рекомендуется также описывать отдельно. Пример описания ресурсной цепи в сетевой модели одноканальной СМО:
RELEASE => R => SEIZE.
Следует быть внимательным при указании путей передвижения меток с атрибутами по сетевой модели, особенно через переход. При задании потока меток через переход источник меток должен быть связан с приемником меток через один и тот же контакт перехода, иначе получается разрыв потока и из источника в приемник метки не попадают. Примеры правильного описания потоков транзакций через переход TG (в генераторе кадров):
PG => TG.. => (PG; QUEUE => ...)
PG => TG..1 => (PG; QUEUE => ...)
PG => TG..1; TG..1 => PG; TG..1 => QUEUE; ...
PG => TG..1 => PG; TG..1 => QUEUE => ...
Однако неправильным будет следующее описание:
PG => TG.. => PG; TG.. => QUEUE => ...
В данном случае позиции PG и QUEUE будут связаны с разными контактами перехода TG. Следует обратить внимание на то, что в позицию QUEUE в этом случае будут поступать простые метки. На рис. 3.2,в,г представлены сетевые модели одноканальной СМО с отказами (см. рис. 3.1,б). Предположим, что емкость оче-реди О1 равна 5. В первой предложенной сетевой модели отказы моделируются следующим образом. Позиция QUEUE объявляется ограниченной, ограниченность позиции полагается равной 5. Это означает, что в любом случае маркировка позиции QUEUE (обозначается как M(QUEUE)), не должна превосходить 5. В случае, если срабатывание какого-либо перехода (в данном случае это переход PUT) привело бы к нарушению данного условия, то этот переход блокируется и становится неразрешенным. Для уничтожения заявки используется переход REJECT. Данный переход является разрешенным всякий раз, когда в позиции Р0 находится метка. Если M(QUEUE) < 5, то при тех же условиях также будет разрешен переход PUT. Среди двух (и более) разрешенных переходов одного приоритета система может выбрать любой в соответствии с разыгранным случайным числом. Однако в данном случае согласно логике функционирования СМО должен сработать переход PUT. Чтобы выполнялось это требование, переходу REJECT присвоен приоритет на единицу меньший приоритета перехода PUT (равно как и приоритетов других переходов). Переход REJECT будет срабатывать, когда не разрешен переход PUT.
Иной вариант решения рассмотренной выше задачи описания механизма отказа предложен на рис. 3.2,г. В этом случае решение произведено с использованием проверочной дуги (QUEUE, REJECT). Данная дуга является разрешенной, если M(QUEUE)>= >= 5. Переходу REJECT присвоен приоритет выше, чем у остальных переходов. При переходе метки в позицию Р0, если M(QUEUE) < 5, переход REJECT не разрешен. В итоге срабатывает переход PUT. Если M(QUEUE) >= 5, разрешены переходы REJECT и PUT, но, поскольку приоритет перехода REJECT выше, срабатывает именно он. Следует обратить внимание на то, что при срабатывании перехода REJECT метки из позиции QUEUE не удаляются, так как атрибут дуги n2 = 0. Описание проверочной дуги может быть следующим: QUEUE<5, 0> => REJECT.
Инициализация представленных сетевых моделей сводится к начальной установке переменной IX, осуществляемой процедурой начальной установки. Процедура начальной установки вводится конструкцией PROC FOR INITIAL и выполняется перед началом имитации.
Вопрос 3,4.
Имитационная модель одноканальной СМО
Имитационная модель многоканальной СМО
Сущность подхода к имитации работы СМО проста— случайный процесс работы системы в интервале [О, T] рассматривается как детерминированный, но со случайно выбранными параметрами. Для обеспечения статистической устойчивости искомых результатов процесс моделирования повторяется заданное количество раз N1. Показатели эффективности формируются на основе статистической обработки результатов отдельных реализаций процесса моделирования.
Итак, рассматривается одноканальная СМО, в которую поступают заявки, образующие ординарный поток однородных событий с заданным законом распределения f(t) интервалов между моментами появления заявок. Заявки поступают в случайные моменты времени tj, они обслуживаются в течение времени τ*j, и обслуживание заканчивается в момент t*j. Случайная величина
длительности обслуживания t* определяется в соответствии с заданным законом распределения f(x*).Судьба последующей заявки зависит (рис. 3, а) от момента ее появления tj относительно момента окончания обслуживания предыдущей t*j-1. Так, если бы рассматривалась СМО с отказами и очередная заявка поступила бы раньше наступления момента окончания обслуживания предыдущей, т. е. tj < t*j-i, то такая заявка получила бы отказ (рис. 3, б), если же tj>=t*j_i, то заявка была бы обслужена (см. рис. 3,а).
■
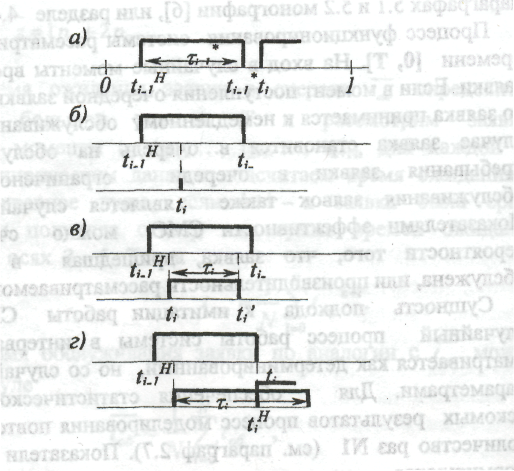
Рис. 3. Детали временной диаграммы
В связи с тем, что в рассматриваемой СМО должно учитываться ограничение времени возможного ожидания, необходимо формировать х} - случайную величину длительности ожидания j-й заявки начала обслуживания с соответствующим законом распределения f(t). Когда tj < t*j.b то j-я заявка получает
отказ (рис. 3, в), если t'j
Фрагмент блок-схемы моделирующего алгоритма
одноканальной СМО представлен на рис. 3.3, а ниже дается описание большинства используемых блоков:
1 - формирование очередного момента tj поступления заявки в систему;
2 - проверка условия tj < Т принадлежности момента
поступления очередной заявки tj интервалу исследования системы
[0,т];
3 - проверка условия tj < t*j_i, где t*j_i - момент окончания
i обслуживания предыдущей заявки;
- - формирование случайного значения длительности ожидания
ij в соответствии с законом распределения f(x);
- - вычисление момента t'j = tj + Xj (в момент t'j заявка
покидает систему, если она не будет принята к обслуживанию);
- * проверка условия t'j < t*j-i (заявка покидает систему
I раньше, чем освободится канал);
- - выбор в качестве момента начала обслуживания j - й
I заявки момента окончания обслуживания (j -1) -й заявки t"j = t*j.b
- - выбор в качестве момента начала обслуживания j - й
заявки момента ее поступления в систему tHj = tj;
- - формирование длительности обслуживания x*j заявки
(времени занятости канала) в соответствии с законом f(x*);
10 - вычисление момента окончания обслуживания j - й
заявки (момента освобождения канала) t*j = tHj + x*j;
11 - проверка условия t*} <= Т;
использованы для построения моделирующего алгоритма в этомслучае. Здесь также сохраняются все использованные выше
обозначения.
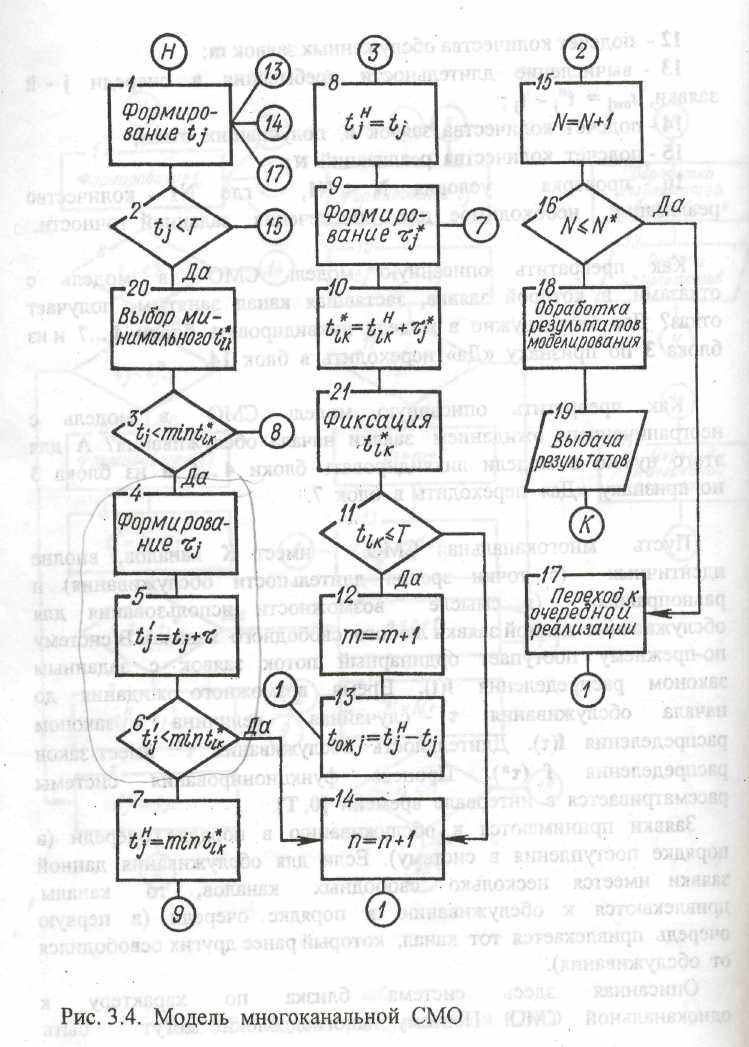
Блок-схема алгоритма многоканальной СМО представлена на рис. 3.4. В ней дополнительно использованы следующие блоки:
3 - проверка условия tj < min t*\k,
- - проверка t' j< min t*ik,
- - выбор в качестве момента начала обслуживания tHj
величины min t*ik,
10 - вычисление момента окончания обслуживания 1-й заявки (момента освобождения к-го канала, Tjc)
t*|k=tн lk+T*j,
где tнlk- момент начала обслуживания 1-й заявки k-м каналом