Моделирование

Вид материала

Документы

Содержание Вопрос №2. Оценка качества последовательностей случайных величин Проверка по моментам Проверка на равномерность. Проверка с помощью вычисления какой-нибудь общеизвестной константы.

Подобный материал:

• Моделирование и формализация Моделирование как метод познания Моделирование, 143.04kb.
• Календарный план учебных занятий по дисциплине Моделирование информационных процессов, 24.12kb.
• Темы курсовых работ по дисциплине «моделирование систем» Ваш № в списке группы, 19.48kb.
• ИнтервальноЕ моделирование свойств сплава, 16.17kb.
• Программа спецкурса "Компьютерное моделирование нелинейных волновых процессов" Специальность, 27.11kb.
• Лекция Моделирование физических процессов, 111.71kb.
• Программа дисциплины имитационное моделирование в экономике для направления 080100., 228.47kb.
• Правительстве Российской Федерации» (Финансовый университет) Кафедра «Математическое, 246.23kb.
• Лекции по дисциплине «Социальное моделирование и программирование», 44.69kb.
• Учебно-методический комплекс по дисциплине "компьютерное моделирование" (факультет, 384.08kb.

Вопрос №2. Оценка качества последовательностей случайных величин

Чтобы быть уверенным в результатах имитационного эксперимента, предварительно необходимо убедиться в случайности используемых последовательностей случайных величин. А качество случайных чисел, получаемых программным способом на компьютере, зависит от того, насколько удачно построен алгоритм, или подобраны коэффициенты и начальные значения параметров генераторов.

Статистическая теория предлагает целый ряд количественных критериев случайности. Однако, если последовательность удовлетворяет относительно тестов Т_1? Т₂, ..., Т„ , все же нет уверенности, что и тест T_n+i она выдержит столь же успешно. И все-таки чем больше тестов прошла последовательность, тем надежнее получаются результаты. Как правило, случайные числа проходят проверку с помощью следующих тестов: универсальных тестов (критерий χ²(«хи-квадрат»), критерий Колмогорова -Смирнова (КС-критерий)) и эмпирических тестов (проверка по моментам распределения, проверка равномерности, проверка серий, проверка интервалов, проверка комбинаций, проверка с помощью вычисления какой-нибудь общеизвестной константы).

Проверка по моментам распределения. Математическое ожидание и дисперсия равномерной случайной последовательности в интервале [0,1] равны 0,5 и 1/12 соответственно. Пусть имеется последовательность чисел ξ,i, ξ,2» ..., ξ _n» полученная с использованием какого-нибудь программного генератора. Для этих чисел



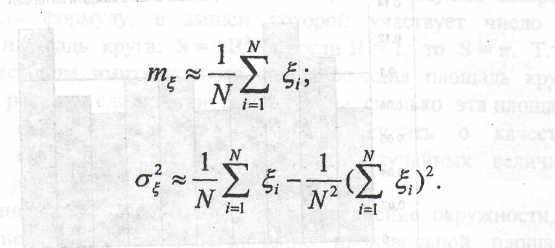
Если генерируемые числа близки к равномерной случайной последовательности в интервале [0,1], то при достаточно больших

N

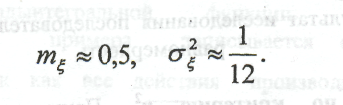
Проверка на равномерность. Интервал [0,1] разбивается на n равных подынтервалов и фиксируется, в какой из подынтервалов попадают числа ξ_i . Пусть m1 - количество случайных чисел, попавших в первый интервал; m₂ - во второй и т.д. При этом

m1 + m2i + ... + m_n = N.

Затем вычисляются частоты попадания случайных чисел в каждый из подынтервалов

p_i=m_i/N

Если случайная последовательность чисел равномерная, то при больших N гистограмма (ломаная линия) должна приближаться к теоретической прямой у=1/n. Если число разбиений равно 10, то у = 0,1. На рис. 2.6 приведены результаты исследования последовательности случайных чисел (для N = 1000), полученных с использованием стандартной функции random языка Паскаль.










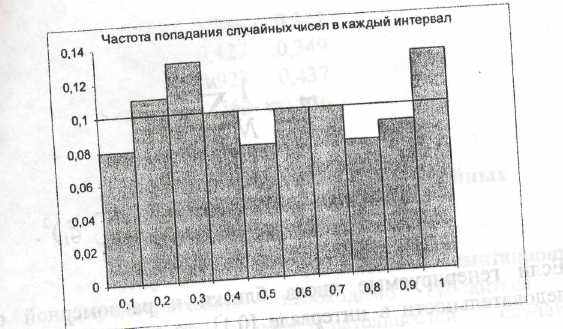
Рис.2,6 Результат исследования последовательности чисел на

равномерность

Проверка по критерию χ²- Применение этого метода основано на следующей процедуре:

1. Отрезок [0,1] разбивается на n подынтервалов (n принимают

равным от 10 до 20).

2. По совокупности N чисел подсчитывается количество m_i,

попавших в i-й подынтервал (i = 1,2, ...,n).


3. Определяется эмпирическое значение

г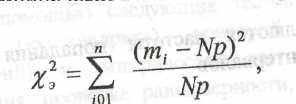де p=l/n.


4. Для доверительной вероятности а и числа степеней
свободы 1 = n - 1 определяется теоретическое значение

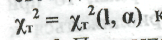критерия,


5. При выполнении условия χ_э²< χ_т² гипотеза о равномерности принимается, в противном случае - признается несостоятельной.

Проверка с помощью вычисления какой-нибудь общеизвестной константы. Для реализации этой проверки выбирается, например, вычисление числа п. Значение его известно и определено с большой точностью: π = 3,1416.... Нужно выбрать какую-нибудь формулу, в записи которой участвует число я. Например, площадь круга: S = πR² и, если R = 1, то S = π. Т. е., вычислив методом имитационного моделирования площадь круга с радиусом, равным единице, и проверив на сколько эта площадь отличатся от величины 3,1416, можно судить о качестве генератора, выдающего последовательность случайных величин, равномерно распределенных в интервале [0,1].

Для вычисления S необходимо знать уравнение окружности, а оно известно: х² + у² = 1. Для этого нужно иметь аналитическое выражение подынтегральной . функции, которое для рассматриваемого примера записывается очень просто

y = ±√(1-x²). Так как все действия производятся в первом координатном углу, то 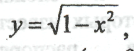и так как вычисляется площадь только четверти круга (рис. 2.3), то искомая величина четверти круга S’ ≈ m / N. А площадь всего круга S и, следовательно, число π ≈ 4 S’ = 4m / N. Здесь m - число точек, попавших при имитационном эксперименте под кривую

у =√1 – х² или на саму кривую, а N - общее количество точек, брошенных в единичный квадрат.

Чем меньше отличается вычисленное значение π от точного (3,1416), тем с большей уверенностью можно считать, что статистические характеристики генератора случайных величин, который использовался при решении этой задачи, являются удовлетворительными. При этом необходимо учитывать, что точность вычисления зависит, конечно, от количества точек, брошенных в единичный квадрат, т.е. от количества реализаций процесса моделирования.