Учебно-методический комплекс по дисциплине "компьютерное моделирование" (факультет прикладной информатики и информационных технологий) для специальности (050202-09-14 R)

Вид материала

Учебно-методический комплекс

Содержание Лабораторные занятия Текущий контроль Учебно-материальная база 1. Пояснительная записка. Лабораторные занятия Текущий контроль Учебно-материальная база 2. Тематический план учебной дисциплины. В т.ч. аудиторных, час 3. Содержание учебной дисциплины. Рекомендации к самостоятельной работе Лабораторная работа № 2. Рекомендации к самостоятельной работе Содержание работы Лабораторная работа № 3. Рекомендации к самостоятельной работе Лабораторная работа № 4. Рекомендации к самостоятельной работе O(5;-2) и радиусом R=2 Форма представления отчета ... Полное содержание

Подобный материал:

• Учебно-методический комплекс по дисциплине компьютерное моделирование (физико-математический, 429.03kb.
• Учебно-методический комплекс учебной дисциплины дпп ф. 11 компьютерное моделирование, 239.02kb.
• Учебно-методический комплекс по дисциплине «теория и методика преподавания информатики», 378.57kb.
• Учебно-методический комплекс по дисциплине «Разработка и стандартизация программных, 278.97kb.
• Учебно-методический комплекс «Высокоуровневые методы информатики и программирования», 569.1kb.
• Учебно-методический комплекс по специальностям 050202. 65 и 050200. 62 «Информатика», 457.74kb.
• Учебно-методический комплекс по дисциплине Основы прогрессивных технологий Направления, 1799.38kb.
• Еремеев Андрей Владимирович, кандидат технических наук, доцент кафедры информационных, 344.4kb.
• Б. В. Мартынов учебно-методический комплекс по дисциплине «логистика» для студентов, 1097.34kb.
• И. Д. Алекперов учебно-методический комплекс дисциплины "информатика" Ростов-на-Дону, 952.05kb.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

АРМАВИРСКАЯ ГОСУДАРСТВЕННАЯ ПЕДАГОГИЧЕСКАЯ АКАДЕМИЯ


Утверждено на заседании кафедры


Зав. кафедрой___________________


УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС

по дисциплине

"КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ"

(ФАКУЛЬТЕТ ПРИКЛАДНОЙ ИНФОРМАТИКИ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ)

для специальности (050202-09-14_R)

"Учитель информатики и математики"

Форма контроля: экзамен

4 курс, 8 семестр.


Программа составлена

доц. Бабенко Т.А.


Армавир 2012

АННОТАЦИЯ

Курс компьютерное моделирование предназначен для подготовки будущих учителей с квалификацией "Учитель информатики и математики" к преподаванию такого раздела школьного курса информатики как «Моделирование».

Изучая предлагаемый курс, учащиеся убеждаются в том, что существуют задачи, которые трудно или невозможно решить без применения компьютеров. Это различного рода задачи моделирования и оптимизации.

Тема «Компьютерное моделирование» может оказаться очень важной, так как дает учащимся возможность провести исследовательскую работу, выполнить анализ полученных результатов, обратить внимание на конечность алгоритма, оценить точность модели, столкнуться с погрешностью приближенных вычислений, увидеть взаимосвязь различных наук и дисциплин, получить удовлетворение от выполненной работы.

В данном курсе рассматриваются следующие разделы: компьютерное моделирование - имитация, численный эксперимент, компьютерная графика и геометрическое моделирование, понятие о математическом моделировании, различные подходы к классификации математических моделей, основные этапы математического моделирования, математическое моделирование детерминированных физических процессов, моделирование стохастических систем, случайные числа, генерирование последовательности случайных чисел с заданным законом распределения, имитационное стохастическое моделирование, математические модели в химии, биологии, экологии, примеры математического моделирования в других областях человеческой деятельности (экономика, сельское хозяйство, эпидемиология и др.), рассмотрены возможности пакета математической поддержки MathLab (пакет моделирования энергетических систем Power System Blockset).

Лекции по курсу проводятся с целью дать слушателям знания по изучаемым темам в наиболее общем, системном виде. В ходе проведения лекции необходимо раскрыть наиболее сложные, узловые вопросы, ставить студентам задачи по самостоятельному изучению материала, как по отдельным вопросам, так и по какой-то проблеме в целом.

После прослушивания лекций и проведения самостоятельной работы студент должен усвоить предложенный материал на уровне “иметь представление”, а отдельные элементы на уровне “знать”.

Более глубокое и конкретное изучение нормативных документов, рекомендуемой литературы, подготовка рефератов, сообщений, докладов осуществляется при проведении самостоятельной работы.

Лабораторные занятия имеют цель дать студентам практические навыки работы с моделями на основе языка программирования Паскаль, а также с программными средствами для моделирования предметно-коммуникативных сред.

Практические занятия целесообразно проводить по схеме: повторение пройденного материала, изучение последовательности выполнения отдельных элементов знания по новой теме, а затем практическое их выполнение на ПК.

Текущий контроль осуществляется при проведении лабораторных работ.

Итоговый контроль проводится в форме экзамена. Порядок его проведения и выносимые вопросы сообщаются студентам заблаговременно, в соответствии с требованиями нормативных документов и деканата факультета.

Учебно-материальная база курса включает нормативные документы высшего профессионального образования, нормативные документы в области информации, информатизации и защиты информации, сборники лекций и другую учебно-методическую литературу, специализированные компьютерные классы и технические средства обучения.


1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.

Курс компьютерное моделирование предназначен для подготовки будущих учителей с квалификацией "Учитель информатики и математики" к преподаванию такого раздела школьного курса информатики как «Моделирование».

Изучая предлагаемый курс, учащиеся убеждаются в том, что существуют задачи, которые трудно или невозможно решить без применения компьютеров. Это различного рода задачи моделирования и оптимизации.

Тема «Компьютерное моделирование» может оказаться очень важной, так как дает учащимся возможность провести исследовательскую работу, выполнить анализ полученных результатов, обратить внимание на конечность алгоритма, оценить точность модели, столкнуться с погрешностью приближенных вычислений, увидеть взаимосвязь различных наук и дисциплин, получить удовлетворение от выполненной работы.

В данном курсе рассматриваются следующие разделы: компьютерное моделирование - имитация, численный эксперимент, компьютерная графика и геометрическое моделирование, понятие о математическом моделировании, различные подходы к классификации математических моделей, основные этапы математического моделирования, математическое моделирование детерминированных физических процессов, моделирование стохастических систем, случайные числа, генерирование последовательности случайных чисел с заданным законом распределения, имитационное стохастическое моделирование, математические модели в химии, биологии, экологии, примеры математического моделирования в других областях человеческой деятельности (экономика, сельское хозяйство, эпидемиология и др.), рассмотрены возможности пакета математической поддержки MathLab (пакет моделирования энергетических систем Power System Blockset).

Лекции по курсу проводятся с целью дать слушателям знания по изучаемым темам в наиболее общем, системном виде. В ходе проведения лекции необходимо раскрыть наиболее сложные, узловые вопросы, ставить студентам задачи по самостоятельному изучению материала, как по отдельным вопросам, так и по какой-то проблеме в целом.

После прослушивания лекций и проведения самостоятельной работы студент должен усвоить предложенный материал на уровне “иметь представление”, а отдельные элементы на уровне “знать”.

Более глубокое и конкретное изучение нормативных документов, рекомендуемой литературы, подготовка рефератов, сообщений, докладов осуществляется при проведении самостоятельной работы.

Лабораторные занятия имеют цель дать студентам практические навыки работы с моделями на основе языка программирования Паскаль, а также с программными средствами для моделирования предметно-коммуникативных сред.

Практические занятия целесообразно проводить по схеме: повторение пройденного материала, изучение последовательности выполнения отдельных элементов знания по новой теме, а затем практическое их выполнение на ПК.

Текущий контроль осуществляется при проведении лабораторных работ.

Итоговый контроль проводится в форме экзамена. Порядок его проведения и выносимые вопросы сообщаются студентам заблаговременно, в соответствии с требованиями нормативных документов и деканата факультета.

Учебно-материальная база курса включает нормативные документы высшего профессионального образования, нормативные документы в области информации, информатизации и защиты информации, сборники лекций и другую учебно-методическую литературу, специализированные компьютерные классы и технические средства обучения.


2. ТЕМАТИЧЕСКИЙ ПЛАН УЧЕБНОЙ ДИСЦИПЛИНЫ.

№ п/п	Раздел, тема	Всего часов	В т.ч. аудиторных, час				Самостоятельная работа, час
			Всего аудит	Из них
				Лекции	Практ	Лабор
1	2	3	4	5	6	7	8
1.	Понятие «модель». Моделирование как метод познания. Натурные и абстрактные модели.	6	2	2			4
2.	Компьютерная модель. Абстрактные модели и их классификация.	6	2	2			4
2.1	Основные структуры в информационном моделировании.	6					6
2.2	Виды моделирования в естественных и технических науках.	4					4
2.3	Моделирование логических устройств без памяти	8	6	2		4	2
2.4	Моделирование логических устройств c памятью. Конечные автоматы.	8	6	2		4	2
3.	Модели динамических систем. Инструментальные программные средства для моделирования динамических систем.
3.1	Моделирование детерминированных физических процессов.	8	4	2		2	4
3.2	Имитационное моделирование.	8	6	2		4	2
3.3	Геометрическое моделирование и компьютерная графика.	6	4	2		2	2
4.	Моделирование стахостических систем. Метод статистических испытаний.	8	6	2		4	2
5.	Моделирование последовательности независимых и зависимых случайных испытаний.	8	6	2		4	2
6.	Общий алгоритм моделирования дискретной случайной величины. Построение гистограмм.	6	4	2		2	2
7.	Модели с сосредоточенными и распределенными параметрами. Дескриптивные, оптимизационные, многокритериальные, игровые модели.	6	2			2	4
8.	Системный подход в научных исследованиях. Численный эксперимент. Его взаимосвязи с натурным экспериментом и теорией.	6					6
9.	Моделирование систем массового обслуживания. Переход детерминированных систем к хаотическому поведению.	6	4	2		2	2
10.	Примеры математических моделей в химии, биологии, экологии, экономике. Учебные компьютерные модели.	8	2			2	6
11.	Программные средства для моделирования предметно-коммуникативных сред (предметной области).	6	4	2		2	2
12.	Специфика использования компьютерного моделирования в педагогических программных средствах.	6	2			2	4
Итого:		120	60	24		36	60

3. СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ.

3.1. Содержание учебного материала.

Лекция № 1. Понятие «модель». Моделирование как метод познания. Натурные и абстрактные модели.

Понятие модели. Определение. Виды моделей. Задача моделирования. Пример моделирования процессов в физики. Моделирование с использованием ЭВМ. Вычислительный эксперимент.


Лекция № 2.

Тема: Компьютерная модель. Абстрактные модели и их классификация.

Классификация моделей. Абстрактные модели. Вербальные модели. Информационные модели. Объекты и их связи. Примеры информационных моделей. Математические модели.


Лекция № 3. Раздел 2.3. Моделирование логических устройств без памяти.

Моделирование работы компонентов ЭВМ. Основные типы логических элементов «И», «ИЛИ», «НЕ». Модели логических элементов. Моделирование сложных комбинационных схем (шифраторы, мультиплексоры и т.д.)


Лекция № 4. Раздел 2.4. Моделирование логических устройств c памятью. Конечные автоматы.

Моделирование устройств с памятью. Автоматы. Определения. Множества, описывающие автоматы. Входной алфавит. Выходной алфавит. Таблица переходов. Таблица выходов. Примеры построения моделей автоматов.


Лекция № 5. Раздел 3.1. Моделирование детерминированных физических процессов.

Из истории моделирования физических процессов. Моделирование задач, не описываемых аналитически. Моделирование динамических процессов. Примеры математических моделей и эксперименты с ними.


Лекция № 6. Раздел 3.2. Имитационное моделирование.

Основные понятия. Задача имитационного моделирования. Области применения имитационного моделирования. Примеры имитационных моделей.


Лекция № 7. Раздел 3.3. Геометрическое моделирование и компьютерная графика.

Компьютерная графика как один из разделов моделирования. Плоская графика.

Динамическая плоская графика. Трехмерная графика. Динамическая трехмерная графика. Учет взаимных пересечений.


Лекция №8. Моделирование стахостических систем. Метод статистических испытаний.

Роль вероятностных событий в описании природных явлений. Детерминированные процессы, содержащие шум. Метод Монте-Карло в моделировании.


Лекция № 9. Моделирование последовательности независимых и зависимых случайных испытаний.

Псевдослучайные числа. Генерирование последовательности равномерно распределенных случайных чисел. Генерирование случайных чисел распределенных по закону распределения Пирсона. Генерирование случайных чисел распределенных по экспоненциальному закону распределения.


Лекция № 10. Общий алгоритм моделирования дискретной случайной величины. Построение гистограмм.

Дискретная случайная величина. Числовые характеристики, описывающие случайные величины: частота, статистическое математическое ожидание, статистическая дисперсия, среднеквадратическое отклонение. Статистическая оценка плотности вероятности. Гистограмма.


Лекция № 11. Моделирование систем массового обслуживания. Переход детерминированных систем к хаотическому поведению.

Системы массового обслуживания. Основные понятия. Моделирование систем массового обслуживания. Оценка основных параметров систем массового обслуживания (очередь, время ожидания и т.д.)


Лекция № 12. Программные средства для моделирования предметно-коммуникативных сред (предметной области).

Программные средства математической поддержки. Система MathLab. Моделирование аналитически описанных процессов. Система MathLab. Моделирование в системах автоматизированного проектирования. Назначение пакета Power System Blockset. Моделирование энергетических систем и устройств. Библиотеки пакета Power System Blockset.


3.2. Содержание лабораторных работ.


Лабораторная работа № 1. Моделирование логических устройств без памяти.


Цель работы: Изучение понятия модель, абстрактные модели, научиться моделировать логические устройства без памяти.


Рекомендации к самостоятельной работе:


Повторить материал лекций по теме: «Моделирование логических устройств без памяти»


Содержание работы:


1. Проработка лекционного материала на практике.

2. Смоделировать побитовую операцию NOT с однобайтовым операндом в 2-ой системе счисления.

3. Смоделировать побитовые операции AND и OR с двухбайтовыми операндами в 2-ой системе счисления.

4. Смоделировать побитовые операции NOT AND, NOT OR с трехбайтовыми операндами 2-ой системе счисления.

5. Построить модель логического устройства (шифратора, дешифратора и т.д.)


Форма представления отчета:

Студент должен продемонстрировать программы на языке Паскаль, показать работу моделей.


Лабораторная работа № 2. Моделирование логических устройств c памятью. Конечные автоматы.


Цель работы: Изучение понятия модель, абстрактные модели, научиться моделировать логические устройства с памятью.


Рекомендации к самостоятельной работе:


Повторить материал лекций по теме: «Моделирование логических устройств c памятью. Конечные автоматы».


Содержание работы:


1. Смоделируйте работу логического устройства, заданного схемой:



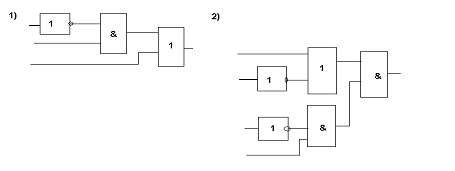
2. Используя базовые логические элементы И, ИЛИ, НЕ, смоделируйте работу устройства, реализующего следующую логику:

a	b	c	F(a,b,c)
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	0

3. Смоделируйте работу устройства из задания 2, используя базисный элемент И-НЕ.

4.Построить автоматную модель с заданными алфавитом, таблицей переходов, таблицей выходов, выходным алфавитом.


Форма представления отчета:

Студент должен продемонстрировать программы на языке Паскаль, показать работу моделей.


Лабораторная работа № 3. Моделирование детерминированных физических процессов.


Цель работы: Изучение понятия модель, абстрактные модели, научиться моделировать детерминированные физические процессы.


Рекомендации к самостоятельной работе:


Повторить материал лекций по теме: «Моделирование детерминированных физических процессов».


Содержание работы:


1. Построить модель, описывающую прыжок с парашютом с учетом сопротивления воздуха.

2. Построить модель движения тела брошенного под углом к горизонту


Форма представления отчета:

Студент должен продемонстрировать программы на языке Паскаль, показать работу моделей.


Лабораторная работа № 4. Имитационное моделирование.


Цель работы: Изучение понятия модель, абстрактные модели, научиться создавать имитационные модели.


Рекомендации к самостоятельной работе:


Повторить материал лекций по теме: «Имитационное моделирование».


Содержание работы:


1. Примените метод Монте-Карло для подсчёта площади:

а) круга с центром в точке O(5;-2) и радиусом R=2;

б) фигуры, ограниченной линиями y=x²-3 и y=6;

в) фигуры, ограниченной линиями y=5/x, y=x-4 и x=1.

Точность вычислений попытайтесь увеличить посредством увеличения числа N.

2. Площадь тех же фигур получите теоретически и сравните с результатами применения метода Монте-Карло.

3. Смоделировать блуждание пьяного человека вдоль прямой, перпендикулярной краю пропасти. Подсчитать вероятность падения в пропасть, если человек находится на расстоянии 5 шагов от края пропасти, а безопасным можно считать расстояние 15 шагов от края.


Форма представления отчета:

Студент должен продемонстрировать программы на языке Паскаль, показать работу моделей.


Лабораторная работа № 5. Геометрическое моделирование и компьютерная графика.


Цель работы: Изучение понятия модель, геометрическое моделирование, научиться создавать модели графическими средствами.


Рекомендации к самостоятельной работе:


Повторить материал лекций по теме: «Геометрическое моделирование и компьютерная графика».


Содержание работы:

1. Программа плоского моделирования.
   
2. Динамическая графика на плоскости.
   
3. Программа пространственного моделирования.
   
4. Динамическая графика в пространстве.
   

Форма представления отчета:

Студент должен продемонстрировать программы на языке Паскаль, показать работу моделей.


Лабораторная работа № 6. Моделирование стахостических систем. Метод статистических испытаний.


Цель работы: Изучение понятия модель, абстрактные модели, научиться создавать модели стахостических систем.


Рекомендации к самостоятельной работе:


Повторить материал лекций по теме: «Моделирование стахостических систем. Метод статистических испытаний».


Содержание работы:

1. Создать модель статистического математического ожидания.
   
2. Создать модель статистической дисперсии.
   
3. Создать модель статистической оценки плотности вероятности.
   

4.. Известно, что рост мужчин некоторой возрастной группы есть нормально распределённая случайная величина X с параметрами a=173 см и σ²=36 см. Определите экспериментально, каковы должны быть доли костюмов 3-го роста (170-176 см) и 4-го роста (176-182 см) в общем объеме производства. Сравните полученные значения с теоретическими.


Форма представления отчета:

Студент должен продемонстрировать программы на языке Паскаль, показать работу моделей.


Лабораторная работа № 7. Моделирование последовательности независимых и зависимых случайных испытаний.


Цель работы: Изучение понятия модель, абстрактные модели, научиться создавать модели последовательности независимых и зависимых случайных испытаний.


Рекомендации к самостоятельной работе:


Повторить материал лекций по теме: «Моделирование последовательности независимых и зависимых случайных испытаний».


Содержание работы:

1. Сгенерировать последовательность случайных чисел, распределенных по равномерному закону распределения.
   
2. Сгенерировать последовательность случайных чисел, распределенных по экспоненциальному закону распределения.
   
3. Сравнить моменты с точными значениями, сделать выводы.
   

Форма представления отчета:

Студент должен продемонстрировать программы на языке Паскаль, показать работу моделей.


Лабораторная работа № 8. Общий алгоритм моделирования дискретной случайной величины. Построение гистограмм.

Цель работы: Изучение понятия модель, абстрактные модели, научиться создавать модели дискретной случайной величины.


Рекомендации к самостоятельной работе:


Повторить материал лекций по теме: «Общий алгоритм моделирования дискретной случайной величины. Построение гистограмм».


Содержание работы:

1. Сгенерировать последовательность случайных чисел, распределенных по нормальному закону распределения.
   
2. Построить гистограмму. Вычислить основные моменты.
   
3. Сравнить моменты с точными значениями, сделать выводы.
   

Форма представления отчета:

Студент должен продемонстрировать программы на языке Паскаль, показать работу моделей.


Лабораторная работа № 9. Модели с сосредоточенными и распределенными параметрами. Дескриптивные, оптимизационные, многокритериальные, игровые модели.


Цель работы: Изучение понятия модель, абстрактные модели, научиться создавать модели с сосредоточенными и распределенными параметрами. Дескриптивные, оптимизационные, многокритериальные, игровые модели.


Рекомендации к самостоятельной работе:


Повторить материал лекций по теме: «Модели с сосредоточенными и распределенными параметрами. Дескриптивные, оптимизационные, многокритериальные, игровые модели».


Содержание работы:

1. Построить модель бросания монеты.
   
2. Построить модель бросания кости.
   
3. Проанализировать результаты. Сделать выводы.
   

Форма представления отчета:

Студент должен продемонстрировать программы на языке Паскаль, показать работу моделей.


Лабораторная работа № 10. Моделирование систем массового обслуживания. Переход детерминированных систем к хаотическому поведению.


Цель работы: Изучение понятия модель, абстрактные модели, научиться моделировать системы массового обслуживания.


Рекомендации к самостоятельной работе:


Повторить материал лекций по теме: «Моделирование систем массового обслуживания. Переход детерминированных систем к хаотическому поведению».


Содержание работы:

1. Построить модель системы массового обслуживания с заданными основными характеристиками (длина очереди, среднее время ожидания).
   
2. Провести вычислительный эксперимент.
   
3. Определить характеристики СМО.
   
4. Сделать выводы.
   

Форма представления отчета:

Студент должен продемонстрировать программы на языке Паскаль, показать работу моделей.


Лабораторная работа № 11. Примеры математических моделей в химии, биологии, экологии, экономике. Учебные компьютерные модели.


Цель работы: Изучение понятия модель, абстрактные модели, научиться создавать математические модели в других областях науки.


Рекомендации к самостоятельной работе:


Повторить материал лекций по теме: «Примеры математических моделей в химии, биологии, экологии, экономике. Учебные компьютерные модели».


Содержание работы:

5. Построить математическую модель процесса обучения.
   
6. Математические модели химии. Модель скорости химической реакции.
   
7. Математические модели в биологии.
   
8. Сделать выводы.
   

Форма представления отчета:

Студент должен продемонстрировать программы на языке Паскаль, показать работу моделей.


Лабораторная работа № 12. Программные средства для моделирования предметно-коммуникативных сред (предметной области).


Цель работы: Изучение понятия модель, абстрактные модели, изучить программные средства для моделирования предметно-коммуникативных сред (предметной области).


Рекомендации к самостоятельной работе:


Повторить материал лекций по теме: «Программные средства для моделирования предметно-коммуникативных сред (предметной области)».


Содержание работы:


План: Пакет математической поддержки MathLab.

Содержание:

1. Назначение пакета и доступ к нему.
   
2. Состав библиотек Power System Blockset.
   
3. Правила подготовки моделей.
   
4. Параметры и единицы измерения.
   

Форма представления отчета:

Студент должен продемонстрировать умение создавать модели в среде MathLab.


Лабораторная работа № 13. Специфика использования компьютерного моделирования в педагогических программных средствах.


Цель работы: Изучение понятия модель, абстрактные модели, специфики использования компьютерного моделирования в педагогических программных средствах.


Рекомендации к самостоятельной работе:


Повторить материал лекций по теме: «Специфика использования компьютерного моделирования в педагогических программных средствах».


Содержание работы:


1. Изучить пакет моделирования энергетических систем Power System Blockset.

2. Построить модель, демонстрирующую суммирование токов от двух источников переменного тока.

3. Построить модель, демонстрирующую суммирование напряжений от двух источников напряжения.

4. Моделирование заряда конденсатора через резистор от источника постоянного напряжения.

5. Выводы.
   

Форма представления отчета:

Студент должен продемонстрировать модели в среде MathLab, показать работу моделей.


4.РЕКОМЕНДАЦИИ ПО ОРГАНИЗАЦИИ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ.


4.1. Список рекомендуемой литературы в библиотеке АГПУ с указанием места хранения.


УДК 518 ББK 32.97 а.з. И-74 (Абонемент)

Информатика: Базовый курс/Под. ред. С.В. Симонович.-Санкт - Петербург: Питер, 2002. -640C.


УДК 518 ББK 32.97 а.з. И-74 (Читальный зал)

Информатика: Базовый курс/Под. ред. С.В. Симонович.-Санкт - Петербург: Питер, 2002. -640C.


УДК 518 ББK 32.81 а.з. И-74 (Абонемент)

Информатика: практикум по технологии работы на компьютере. Под. ред. Н.В. Макаровой. Изд. 3-е, перераб. и доп.-Москва: Финансы и статистика, 2001. -256C.


УДК 518 ББK 32.81 а.з. И-74 (Читальный зал)

Информатика: практикум по технологии работы на компьютере. Под. ред. Н.В. Макаровой. Изд. 3-е, перераб. и доп.-Москва: Финансы и статистика, 2001. -256C.


УДК 6Ф7 ББK 32.81 а.з. М-74 (Абонемент)

Могилев А.В. и др.

Информатика: учеб. пособие для пед. вузов./ Могилев А.В., Пак Н.И., Хеннер Е.К.-Москва: АСАDEMIA, 1999. -816C.


УДК 6Ф7 ББK 32.81 а.з. М-74 (Техфак)

Могилев А.В. и др.

Информатика: учеб. пособие для пед. вузов./ Могилев А.В., Пак Н.И., Хеннер Е.К.-Москва: АСАDEMIA, 1999. -816C.


УДК 6Ф7 ББK 32.81 а.з. М-74 (Читальный зал)

Могилев А.В. и др.

Информатика: учеб. пособие для пед. вузов./ Могилев А.В., Пак Н.И., Хеннер Е.К.-Москва: АСАDEMIA, 1999. -816C.


УДК 518 ББK 32.81 а.з. И-74 (Читальный зал)

Информатика: практикум по технологии работы на компьютере. Под. ред. Н.В. Макаровой. Изд. 3-е, перераб. и доп.-Москва: Финансы и статистика, 2001. -768C.


УДК 518 ББK 32.81 а.з. О-76 (Читальный зал)

Острейковский В.А.

Информатика: учеб. для техн. направлений и спец. вузов.-Москва: Высш. шк., 1999. -512C.


Для подготовки к лабораторным работам, рекомендуется использовать сборник заданий


ссылка скрыта


1) Проработка лекционного материала.

2) Работа с дополнительной литературой.

a) к лекции № 1
основная [1], [7] c.13-30, [14];
дополнительная [12],[13],[26],[29]. (4 часа)

b) к лекции № 2
основная [1], [7] c.50-60, [14], [20], [27];
дополнительная [23],[29]. (4 часа)

c) к лекции № 3
основная [1], [2] c.25-39, 54-92, [3] c.59-81, [4] c.21-84, [5] c32-65; 114-179, [6] c.3-14; [7] c/61-76 (6 часа)

d) к лекции № 4
основная [2] c.40-53, 93-101, 108-115, [3] c.82-97, [4] c.85-139, [5] c.66-102, 202-247. (4 часа)

e) к лекции № 5
основная [2] c.116-124, 146-168, [3] c.217-253, [4]c.230-247, [5] c.264-292, [8] c.80-103;
дополнительная [27]. (2 часа)

f) к лекции № 6
основная [7] c.83-98, [10] c.4-11, [19;
дополнительная [15], [18]. (2 часа)

i) к лекции № 7
основная [20] (2 часа)

g) к лекции № 8
основная [7] c. 114-121. (2 часа)

h) к лекции № 9
основная [7] c. 122-138. (2 часа)

i) к лекции № 10
основная [7] c. 155-173. (2 часа)

j) к лекции № 11
основная [7] c. 177-187, [8] c.4-42,[9] c. 8-14, [16] с. 250-260. (2 часа)

k) к лекции № 12
основная [7] c. 264-338, [9] c.39-48, [16] с. 250-260. (2 часа)

3) Подготовка к лабораторным занятиям.
Изучить литературу:

a) к лаб. раб. № 1 [2] с.25-142;

b) к лаб. раб. № 2 [3] с.59-97;

c) к лаб. раб. № 3 [4] c.21-139;

d) к лаб. раб. № 4 [2]c.146-168, [3] c.217-253, [4] c.230-247;

e) к лаб. раб. № 5 повторить пройденное; (2 часа)

f) к лаб. раб. № 6 [4] c.200-210; (2 часа)

g) к лаб. раб. № 7 [4] c.213-220; (2 часа)

h) к лаб. раб. № 8 [2] c.25-142; (2 часа)

i) к лаб. раб. № 9 [11] c.147-156. (2 часа)

j) к лаб. раб. № 10 [2] c.3-12, 25-39; [3] c.8-35, 59-68; [4] c.21-42; [5] c. 5-15, 32-65; [6] c.15-20; [7] c.177-178. (2 часа)

k) к лаб. раб. № 11 [3]c.98-107,[4]c.140-141, [9] c. 70-72, [16] с. 250-260. (2 часа)

l) к лаб. раб. № 12, 13 [3]c.124-130,[4]c.166-199, [9] c. 87-95, [16] с. 250-260. (2 часа)


Самостоятельная работа студентов состоит в изучении рекомендуемой литературы, проработке лекционного материала, выполнения предложенных заданий.

Для подготовки к лабораторным занятиям рекомендуется самостоятельная работа с ЭВМ во время консультаций преподавателей кафедры информатики.


5. ВОПРОСЫ ЭКЗАМЕНА ПО КОМПЬЮТЕРНОМУ МОДЕЛИРОВАНИЮ.

1. Понятие модели. Определение. Виды моделей. Задача моделирования.
   
2. Примеры моделирования процессов в физики. Моделирование с использованием ЭВМ. Вычислительный эксперимент.
   
3. Этапы компьютерного моделирования. Постановка задачи и ее содержательный анализ. Формализация задачи.
   
4. Этапы компьютерного моделирования. Составление алгоритма. Написание программы. Анализ результатов. Цикличность процессов моделирования.
   
5. Моделирование детерминированных физических процессов.
   
6. Моделирование логических устройств без памяти. Моделирование работы компонентов ЭВМ. Основные типы логических элементов «И», «ИЛИ», «НЕ». Модели логических элементов.
   
7. Моделирование логических устройств без памяти. Моделирование сложных комбинационных схем (дешифраторы, сумматоры и т.д.)
   
8. Моделирование логических устройств c памятью. Конечные автоматы. Моделирование устройств с памятью. Автоматы. Определения. Множества, описывающие автоматы.
   
9. Моделирование логических устройств c памятью. Конечные автоматы. Примеры построения моделей автоматов.
   
10. Стохастическое моделирование. Основные понятия. Роль вероятностных событий в описании природных явлений. Детерминированные процессы, содержащие шум.
    
11. Метод Монте-Карло в моделировании.
    
12. Генерирование случайных чисел. Псевдослучайные числа. Генерирование последовательности равномерно распределенных случайных чисел.
    
13. Генерирование случайных чисел. Генерирование случайных чисел распределенных по экспоненциальному закону распределения.
    
14. Генерирование случайных чисел. Генерирование случайных чисел распределенных по нормальному закону распределения.
    
15. Оценка достоверности гипотезы распределения. Критерий «Х квадрат».
    
16. Имитационное моделирование. Основные понятия. Задача имитационного моделирования. Области применения имитационного моделирования. Примеры имитационных моделей.
    
17. Моделирование потоков случайных событий. Системы массового обслуживания. Основные понятия. Моделирование систем массового обслуживания.
    
18. Моделирование потоков случайных событий. Оценка основных параметров систем массового обслуживания (очередь, время ожидания и т.д.)
    
19. Системы массового обслуживания. Формула Литтла.
    
20. Компьютерная графика. Компьютерная графика как один из разделов моделирования. Плоская графика. Динамическая плоская графика.
    
21. Компьютерная графика. Трехмерная графика. Динамическая трехмерная графика. Учет взаимных пересечений.
    
22. Математические модели в других областях человеческой деятельности. Модели денежных потоков.
    
23. Математические модели в других областях человеческой деятельности.
    
24. Программные средства для моделирования физических процессов (Пакет математической поддержки MathLab).
    
25. Пакет моделирования энергетических систем Power System Blockset.
    

Типовые задачи к экзамену


1. Смоделировать побитовые операции AND и OR с двухбайтовыми операндами в 2-ой системе счисления.

2. Смоделировать арифметическую операцию сложения трех операндов в 2-ой системе счисления.

3. Смоделировать операцию инвертирования битов четырехбайтового операнда, заданного в 2-ой системе счисления.

4.Смоделируйте работу логического устройства, заданного схемой:




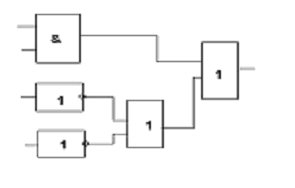
5. Используя базовые логические элементы И, ИЛИ, НЕ, смоделируйте работу устройства, реализующего следующую логику:

a	b	c	F(a,b,c)
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	1

6. Используя базовый логический элемент И-НЕ, смоделируйте работу устройства, реализующего следующую логику:

A	b	C	F(a,b,c)
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	1

7. Примените метод Монте-Карло для подсчёта площади фигуры, ограниченной линиями y=x²-3 и y=6. Точность вычислений увеличивайте посредством увеличения числа N.

8. Площадь той же фигуры получите теоретически и сравните с результатами применения метода Монте-Карло.


6.СПИСОК РЕКОМЕНДУЕМОЙ ДЛЯ ИЗУЧЕНИЯ ЛИТЕРАТУРЫ.

Основная литература.

1. Компьютеры, модели, вычислительный эксперимент. Введение в информатику с позиции математического моделирования / Авт. пред. А.А. Самарский. - М.: Наука, 1988.
   
2. Коршунов Ю.М. Математические основы кибернетики: Учеб. пособие для вузов. - М.: Энергоатомиздат, 1987.
   
3. Вентцель Е.С. Исследование операций: задачи, принципы, методология. М.: Наука, 1988.
   
4. Лазарев В.Г. Проектирование дискретных устройств автоматики: Учеб. пособие для вузов связи. - М.: Радио и связь, 1985.
   
5. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. - М.: Энергоатомиздат, 1988.
   
6. Геронимус Ю.В. Игра, модель, экономика. - М.: Знание, 1989.
   
7. Таха Х. Введение в исследование операций: В 2-х книгах. Кн.2. Пер. с англ. - М.: Мир, 1985.
   
8. Рождерс Д. Алгоритмические основы машинной графики: Пер. с англ. - М.: Мир, 1989.
   
9. Львовский Е.Н. Статистические методы построения эмпирических формул: Учеб. пособие для втузов. М.: Высш. шк., 1988.
   
10. Бочаров П.П., Печинкин А.В. Математическая статистика: Учебное пособие. М.: Изд-во РУДН, 1994.
    
11. Саати Т., Кернс К., Аналитическое планирование. Организация систем: Пер. с англ. - М.: Радио и связь, 1991.
    
12. Смирнов Н.В., Дунин-Барковский И.В. Курс теории вероятностей и математической статистики для технических приложений. М.: Наука, 1969.
    
13. Чистяков В.П. Курс теории вероятностей. М.: Наука, 1982.
    
14. Ногин В.Д., Протодьяконов И.О., Евлампиев И.И. Основы теории оптимизации: Учеб. пособие для студентов втузов. М.: Высш. шк., 1986.
    
15. Бочаров П.П., Печинкин А.В. Теория вероятностей: Учебное пособие. - М.: Изд-во РУДН, 1994.
    
16. Дьяконов В., Круглов В. MathLab. Анализ, идентификация и моделирование систем. Спецсправочник. СПб, 2002.
    

Дополнительная литература.

17. Статистические методы для ЭВМ / Под ред. К. Энслейна, Э. Рэлстона, Г.С. Уилфа: Пер. с англ. - М.: Наука. 1986.
    
18. Пугачев В.С. Введение в теорию вероятностей. М.: Наука, 1968.
    
19. Дегтярев Ю.И. Исследование операций: Учеб. для вузов по спец. АСУ. - М.: Высш. шк., 1986.
    
20. Морозов В.В., Сухарев А.Г., Федоров В.В. Исследование операций в задачах и упражнениях: Учеб. пособие для студентов вузов, обуч. по специальности «Прикладная математика». - М.: Высш. шк., 1986.
    
21. Вентцель Е.С., Овчаров Л.А. Теория вероятностей и ее инженерные приложения. - М.: Наука. 1988.
    
22. Питмен Э. Основы теории статистических выводов: Пер. с англ. - М.: Мир, 1986.
    
23. Бухарев Р.Г. Основы теории вероятностных автоматов. - М.: Наука, 1985.
    
24. Сакович В.А. Оптимальные решения экономических задач. М.: Высш. шк., 1982.
    
25. Франс Дж., Торили Дж. Х. М. Математические модели в сельском хозяйстве. М.: Агропромиздат, 1987.
    
26. Юдин Д.Б., Юдин А.Д. Экстремальные модели в экономике. - М.: Экономика, 1979.
    
27. Математические методы в социальных науках. Сб. статей под ред. П. Лазарьфельда и Н. Генри. М.: Издательство «Прогресс», 1973.
    
28. Ермолаев Ю.М., Ястремский А.И. Стохастические модели и методы в экономическом планировании. М.: Наука, 1979.
    
29. Цветков А.Н., Епанечников В.А. Прикладные программы для микро ЭВМ «Электроника Б3-34». - М.: Финансы и статистика, 1984.
    

30.Робертс Ф.С. Дискретные математические модели с приложениями к социальным, биологическим и экологическим задачам. - М.: Наука. 1986.

31.Дьяконов В. MathLab 6. Учебный курс –Спб, 2001.

32.Дьяконов В., Абраменкова И. MathLab. Обработка сигналов и изображений. Спецсправочник., СПб, 2002.