Geum.ru

Моделирование

Вид материалаДокументы

Содержание


Вопрос №5. Необходимое число реализаций процесса моделирования
Закон распределения частоты события при большом числе опытов
Подобный материал:
1   2   3   4   5   6   7   8   9

Вопрос №5. Необходимое число реализаций процесса моделирования


Величины, получаемые в результате исследования различных процессов методом имитационного моделирования, обычно являются случайными, потому что в основу метода положено использование предельных теорем теории вероятностей]:

Теорема 2.3. При неограниченном увеличении числа опытов N частота события А сходится по вероятности к его вероятности.

Теорема 2.4. При достаточно большом числе независимых опытов N среднее арифметическое наблюдаемых значений случайной величины сходится по вероятности к ее математическому ожиданию.

Таким образом, для обеспечения статистической устойчивости соответствующие оценки вычисляются по большому количеству реализаций. Справедливо спросить, насколько велика ошибка от замены вероятности события его частотой, а математического ожидания - средним арифметическим? И каково должно быть число реализаций N для того, чтобы эта ошибка с практической достоверностью не вышла за данные пределы? То есть, ставится вопрос об оценке точности характеристик случайного процесса.

Пусть в качестве оценки для некоторого параметра а, оцениваемого по результатам моделирования хь выбирается величина х, являющаяся функцией от Xj. В силу случайных причин х будет в общем случае отличаться от а. Это отличие характеризуется следующим образом.

Величину е, когда







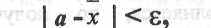
называют точностью оценки х, а вероятность а того, что неравенство выполняется, ее достоверностью. Тогда



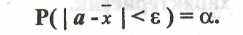
Таким образом, если для оценки параметра а систематически используется величина х, с точностью е и достоверностью а, то в среднем на каждые 100 случаев применения этого правила,

в 100а случаях х будет отличаться от а меньше, чем на е, и

только в (1— а)*100 случаях разница между ними может превосходить s.

При ответе на все поставленные вопросы

пользуются центральной предельной теоремой теории вероятностей Согласно этой теореме принимается, что при большом числе опытов N их средний результат (частота события А или среднее арифметическое наблюдаемых значений случайной величины х) распределяется приближенно по нормальному закону.

Закон распределения частоты события при большом числе опытов

Пусть моделируется событие А, имеющее вероятность появления р. Обозначим через Xj величину, равную единице, если на i-м испытании произошло событие А, и равную нулю, если событие А не произошло. Тогда общее количество ис­пытаний, в течение которых событие А произошло,



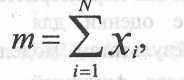
где N — общее число испытаний. Отдельные испытания

считаются независимыми.

Можно определить математическое ожидание Мх-, и дисперсию a2xi случайной величины Xj:







■

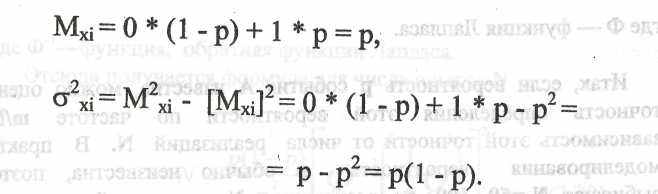
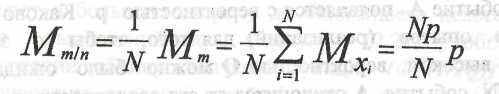
и дисперсию

Частота появления события А равна m/N и является случайной величиной, имеющей математическое ожидание:


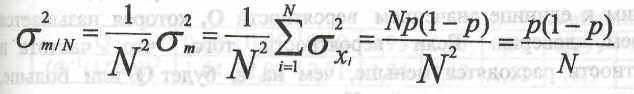5.19

Теперь можно поставить и решить следующие задачи.

Задача 1. Произведено N независимых реализаций, в каждой из которых событие А появляется с вероятностью р. В результате этих опытов получена частота m/N события А. Найти вероятность того, что частота m/N отличается от вероятности р не больше, чем на заданную величину е > 0.

Решение. Считая число N достаточно большим для того, чтобы полагать частоту m/N распределенной по нормальному закону с характеристиками (5.18) и (5.19), получают:



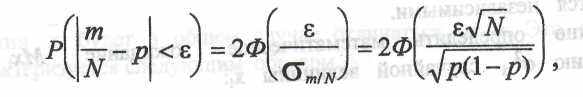
где Ф — функция Лапласа.

Итак, если вероятность р события А известна, можно оценить точность определения этой вероятности по частоте m/N и зависимость этой точности от числа реализаций N. В практике моделирования вероятность р обычно неизвестна, поэтому выбирают No=5O...lOO, по результатам No реализаций определяют m/No, а затем принимают, что р ≈ m/No.

Задача 2. Производится ряд независимых опытов, в каждом из которых событие А появляется с вероятностью р. Каково должно быть число опытов (реализаций) для того, чтобы с заданной, достаточно высокой вероятностью Q можно было ожидать, что частота m/N события А отклонится от его вероятности р меньше, чем на е?

и разрешим уравнение (2.21) относительно N:


Решение. Необходимо задаться каким-нибудь достаточно близким к единице значением вероятности Q, которая называется уровнем доверия. Если вероятность того, что частота и вероятность расходятся меньше, чем на е, будет Q или больше, считают задачу решенной. На практике уровень доверия Q выбирается значением, близким к единице, например, 0,95, 0,99 или 0,995 и т.д., в зависимости от важности задачи, которая преследуется. Предположим, что вероятность Q задана. При­равняем этому значению Q правую часть равенства (2.20):












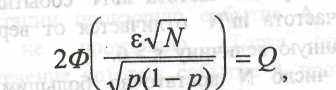
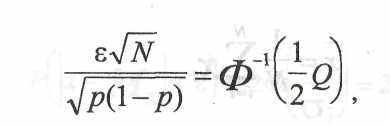
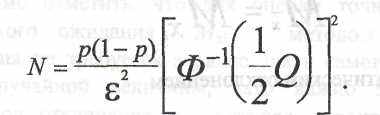
где Ф"1—функция, обратная функции Лапласа. Отсюда получается формула для числа опытов N:


5.22

Если по формуле (5.22) N оказывается не целым, его округляют в большую сторону до ближайшего целого.

Для вычислений по формуле (5.22) удобно иметь в распоряжении таблицу значений функции (Ф-1(1/2Q))2 . В таблице 2.4 приведены значения этой функции для некоторых величин уровня доверия Q.

Закон распределения среднего арифметического при большом числе опытов

Пусть моделируется процесс, в котором при каждом из N независимых испытаний, случайная величина к принимает значения:

Xj, X2..., Xj,..., Х„.

Предположим, что эта величина обладает конечным

математическим ожиданием Mxj и дисперсией a2xi. Тогда среднее арифметическое



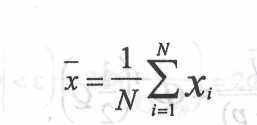
распределяется приближенно по нормальному закону с ма­тематическим ожиданием



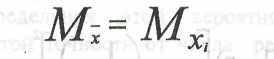
и средним квадратическим отклонением