Geum.ru

Моделирование

Вид материалаДокументы

Содержание


Вопрос №7. Марковские случайные процессы
Рис.15.1. Граф состояний системы
Подобный материал:
1   2   3   4   5   6   7   8   9

Вопрос №7. Марковские случайные процессы


Случайный процесс, протекающий в системе, называется Марковским, если для любого момента времени t0 вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент t0 и не зависят от того, когда и как система пришла в это состояние.

Пусть в настоящий момент t0 система находится в определенном состоянии S0. Мы знаем характеристики состояния системы в настоящем и все, что было при t < t0 (предысторию процесса). Можем ли мы предугадать (предсказать) будущее, т.е. что будет при t > t0? В точности – нет, но какие-то вероятностные характеристики процесса в будущем найти можно. Например, вероятность того, что через некоторое время система S окажется в состоянии S1 или останется в состоянии S0 и т.д.

Пример. Система S – группа самолетов, участвующих в воздушном бою. Пусть x – количество «красных» самолетов, y – количество «синих» самолетов. К моменту времени t0 количество сохранившихся ( не сбитых) самолетов соответственно – x0, y0. Нас интересует вероятность того, что в момент времени численный перевес будет на стороне «красных». Эта вероятность зависит от того, в каком состоянии находилась система в момент времени t0, а не от того, когда и в какой последовательности погибали сбитые до момента t0 самолеты.

На практике Марковские процессы в чистом виде обычно не встречаются. Но имеются процессы, для которых влиянием «предистории» можно пренебречь. И при изучении таких процессов можно применять Марковские модели (в теории массового обслуживания рассматриваются и не Марковские системы массового обслуживания, но математический аппарат, их описывающий, гораздо сложнее).

В исследовании операций большое значение имеют Марковские случайные процессы с дискретными состояниями и непрерывным временем.

Процесс называется процессом с дискретным состоянием, если его возможные состояния S1, S2, … можно заранее определить, и переход системы из состояния в состояние происходит «скачком», практически мгновенно.

Процесс называется процессом с непрерывным временем, если моменты возможных переходов из состояния в состояние не фиксированы заранее, а неопределенны, случайны и могут произойти в любой момент.

Далее рассматриваются только процессы с дискретным состоянием и непрерывным временем.

Пример. Технологическая система (участок) S состоит из двух станков, каждый из которых в случайный момент времени может выйти из строя (отказать), после чего мгновенно начинается ремонт узла, тоже продолжающийся заранее неизвестное, случайное время. Возможны следующие состояния системы:

S0 - оба станка исправны;

S1 - первый станок ремонтируется, второй исправен;

S2 - второй станок ремонтируется, первый исправен;

S3 - оба станка ремонтируются.

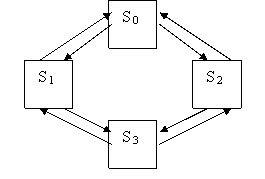
Рис.15.1. Граф состояний системы

Переходы системы S из состояния в состояние происходят практически мгновенно, в случайные моменты выхода из строя того или иного станка или окончания ремонта.

При анализе случайных процессов с дискретными состояниями удобно пользоваться геометрической схемой – графом состояний. Вершины графа – состояния системы. Дуги графа – возможные переходы из состояния в

состояние. Для нашего примера граф состояний приведен на рис.15.1.

Примечание. Переход из состояния S0 в S3 на рисунке не обозначен, т.к. предполагается, что станки выходят из строя независимо друг от друга. Вероятностью одновременного выхода из строя обоих станков мы пренебрегаем.


Вопрос 7. версия 2


Марковский процесс, важный специальный вид случайных процессов, имеющих большое значение в приложениях теории вероятностей к различным разделам естествознания и техники. Примером М. п. может служить распад радиоактивного вещества. Известно, что вероятность распада данного атома за малый промежуток времени dt равна adt, где a — постоянная, характеризующая интенсивность распада данного радиоактивного вещества; эта вероятность не зависит от судьбы всех других атомов и от возраста данного атома. Пусть N обозначает число атомов радиоактивного вещества в некоторый начальный момент времени t = 0 и Pn(t) — вероятность того, что к моменту времени t распалось n атомов. Вероятности Pn(t) удовлетворяют системе дифференциальных уравнений



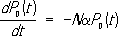
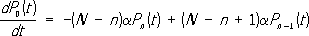
Решая эту систему уравнений при начальных данных

P0(0) = 1, Pn(0) = 0, 1 £ n £ N,

Получаем



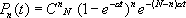
В этом примере в каждый момент времени имеется либо 0, либо 1, либо 2, ..., либо N распавшихся атомов, причём число их характеризует состояние изучаемого явления.


Рассмотренный пример укладывается в следующую более общую схему. Пусть всевозможными состояниями изучаемой системы являются w1, w2, ..., wn, ... в конечном или бесконечном числе. В каждый момент времени система может находиться в одном из этих состояний, и с течением времени происходят случайные переходы из одного состояния в другое. Процесс называют марковским, если состояние системы wi в некоторый момент времени определяет лишь вероятность pij(t) того, что через промежуток времени t система будет находиться в состоянии wj, причём эта вероятность не зависит от течения процесса в предшествующий период. Вероятности pij(t) называют переходными вероятностями. При очень широких условиях переходные вероятности М. п. удовлетворяют конечной или бесконечной системе линейных однородных обыкновенных дифференциальных уравнений.


Теория М. п. возникла на основе исследований А. А. Маркова (старшего), который в работах 1907 положил начало изучению последовательностей зависимых испытаний и связанных с ними сумм случайных величин. Это направление исследований известно под названием теории цепей Маркова. В теории цепей Маркова рассматриваются такие системы, которые могут переходить из одного состояния в другое лишь во вполне определённые моменты времени ti, ti, ... , tk, ... Пусть pij обозначает вероятность того, что система в момент времени tk+1 находится в состоянии wj, если известно, что в момент времени tk она находилась в состоянии wi. Исследование цепей Маркова можно свести к изучению матриц переходных вероятностей . Вместе с тем ряд физиков и техников в своих исследованиях показали важность процессов, в которых рассматриваемая система претерпевает случайные изменения в зависимости от некоторого числа непрерывно меняющихся параметров (времени, координат и т. п.). Исследования этого направления не имели прочной логической основы. Общая теория М. п. и их классификация были даны советским математиком А. Н. Колмогоровым в 1930. Его исследования дали логически безупречную математическую основу общей теории М. п., охватывающей, наряду с процессами описанного выше вида, также процессы типа диффузии, в которых состояние системы характеризуется непрерывно изменяющейся координатой диффундирующей частицы.


В этом случае вместо переходных вероятностей естественно рассматривать соответствующие плотности вероятностей f(t, х, у). Тогда f(t, х, у) есть вероятность того, что частица, находившаяся в точке х, через промежуток времени t будет иметь координату, заключённую между у и y+dy. Колмогоров показал (при некоторых общих условиях), что плотности f(t, х, у) удовлетворяют следующему дифференциальному уравнению с частными производными



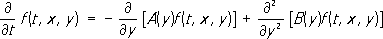
которое ранее было введено для важного в физике специального случая процесса диффузии немецкими физиками А. Фоккером и М. Планком. В этом уравнении коэффициент A(y) представляет собой среднюю скорость изменения координаты у, а коэффициент В(у) — интенсивность случайных колебаний около этой средней. Указанное уравнение явилось источником для многих исследований по теории М. п. в СССР и за рубежом.