Computer Using Educators Inc., Usa материалы
| Вид материала | Документы |
- Computer Using Educators Inc., Usa материалы, 4875.63kb.
- Computer Using Educators, Inc., Usa центр новых педагогических технологий Московский, 5685.88kb.
- Computer Using Educators, Inc., Usa федерация Интернет Образования Центр новых педагогических, 2693.99kb.
- Система Автоматизации Инженерного Труда cad computer Automation Design cam computer, 35.46kb.
- А. Н. Туполева утверждаю: Проректор по учебной и методической работе И. К. Насыров, 271.38kb.
- Задачи обработки изображения : Устранение дефектов изображения (напр., устранение снега, 98.28kb.
- Computer Logic Group Уважаемые гости нашего семинар, 51.71kb.
- Computer Science Students : Учеб пособие для вузов /Сост. Т. В. Смирнова, М. Ю. Юдельсон., 465.89kb.
- Институт Альберта Эйнштейна Издано в 2009 году в Соединенных Штатах Америки Авторское, 1202.95kb.
- A glossary of computer terms download to desktop…, 743.72kb.
ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРА ПРИ ИЗУЧЕНИИ МАТЕМАТИЧЕСКИХ ДОКАЗАТЕЛЬСТВ В СРЕДНЕЙ ШКОЛЕ
Лукьянова Е.В. (Lukyanovalv@list.ru)
Московский педагогический Государственный университет, г. Москва
Одной из важнейших методических проблем является проблема обучения доказательству. Этой проблемой занимались и занимаются многие специалисты в области методики преподавания математики. Обучение доказательству необходимо на всех этапах изучения математики. В курсе геометрии 10 класса есть возможность более тщательно проанализировать и изучить доказательства некоторых теорем. Первые уроки стереометрии посвящены аксиомам стереометрии, а значит, на этих уроках следует напомнить учащимся и обсудить с ними аксиоматический метод построения геометрии. Кроме того, на этих уроках уместно уделить особое внимание доказательствам. Первые теоремы стереометрии достаточно просты, однако доказательствам этих утверждений не уделяется должного внимания, а ведь логическая структура доказательств как раз простых утверждений может быть подробно разобрана и проанализирована.
Возникает проблема: как сделать поиск доказательства и анализ логической структуры готового доказательства доступными и наглядными для учащихся. При решении этой проблемы недостаточно внимания уделяется наглядности процесса рассуждения. Возникает вопрос: "Можно ли сделать процесс поиска доказательства наглядным и, если это возможно, то каким образом это может быть сделано на уроке?".
Реализовать принцип наглядности в обучении позволяет использование компьютера на уроках математики. При этом обычно с помощью компьютера происходит построение графиков, чертежей, изображений тел и их комбинаций и т.д., то есть объектов, которые сами по себе являются средствами наглядности. Но насколько такое использование информационных технологий позволяет сделать более понятным доказательство? Само доказательство при этом не становится для учащихся более простым и иногда внимание учащихся обращено на рисунки, а не на рассуждение. Можно ли с помощью компьютера реализовать принцип наглядности в процессе поиска и построения доказательств?
Существуют средства математической логики, позволяющие сделать более наглядным поиск доказательства и отдельные (простейшие) шаги доказательства. Такие средства предоставляют системы естественного вывода. Формализованные в виде правил вывода элементарные рассуждения позволяют выявить шаги процесса построения доказательства, что дает возможность проследить и зафиксировать ход рассуждения при поиске доказательства. Эти средства в сочетании с использованием компьютера позволяют промоделировать процесс рассуждения и продемонстрировать динамику этого процесса "в замедленном темпе".
Информационные технологии, в частности мультимедиа-презентации (PowerPoint), позволят учителю реализовать принцип наглядности при обучении доказательству. С помощью анимации в презентациях можно сделать визуальным процесс рассуждения при поиске доказательства и зафиксировать элементарные шаги этого рассуждения. Дискретность процесса рассуждения позволяет зафиксировать элементарные шаги, а анимация предложений, используемых на обсуждаемом шаге рассуждения, позволит наглядно продемонстрировать их логическую связь и те соображения, по которым делается шаг рассуждения.
Использовать такие презентации лучше всего в том случае, когда на уроке изучаются утверждения, имеющие относительно простую логическую структуру и относительно небольшое доказательство, например, такое: "Если две прямые параллельны третьей прямой, то они параллельны". Изучение таких утверждений и их доказательств на уроке лучше всего провести в форме фронтальной беседы эвристического характера. Фрагмент урока, на котором планируется рассматриваемое использование компьютера, может быть построен следующим образом.
1. Учитель формулирует утверждение и обсуждает с учащимися логическую структуру этого утверждения в следующей последовательности: восстановление кванторных слов; обсуждение связующих логических слов, присутствующих в утверждении.
2. Учитель еще раз повторяет уточненную формулировку утверждения и обсуждает с учащимися метод доказательства утверждений вида xP(x). Затем, записывает на доске первый шаг доказательства (это же появляется на слайде). Например, для указанной выше теоремы первые слова доказательства следующие: "Пусть a, b и c произвольные прямые. Докажем, что а||с и b||с → а||b".
3. Учитель обсуждает с учащимися следующие шаги доказательства (без записи). Стоит отметить, что в данном случае рекомендуется записывать текст доказательства именно после этого обсуждения, для того чтобы учащиеся не отвлекались от поиска доказательства.
На слайде, одновременно с рассуждением, постепенно один за другим отражаются шаги построения доказательства. Анимация (движение и выделение цветом утверждений – членов доказательства), в данном случае, позволит не только выделить соответствующий шаг доказательства, но и продемонстрировать, по каким соображениям сделан очередной переход. К тому же, при необходимости можно скрыть или, наоборот, восстановить тот или иной шаг в доказательстве. Последний слайд содержит полученную в ходе поиска схему доказательства в виде дерева, отражающую логическую структуру доказательства, логические связи между членами доказательства.
4. Учитель записывает доказательство на доске или поручает запись одному из учащихся. Презентация повторяется еще раз синхронно с записью доказательства на доске, на слайдах шаги доказательства появляются в том же порядке, в каком они появлялись и обсуждались при поиске доказательства.
Таким образом, моделирование процесса рассуждения с помощью средств естественного вывода в сочетании с использованием компьютерной анимации позволяет отразить динамику процесса рассуждения.
Литература
1. Тимофеева И.Л. О логических эвристических средствах построения доказательств // Математика в школе. – 2004. – № 10. – С. 42–50.
2. Тимофеева И.Л., Лукьянова Е.В. Моделирование элементарных рассуждений с помощью программы Power Point. // Сб. материалов XVII Международной конф. «Применение новых технологий в образовании» – Троицк, 2006. – С. 236-238.
FORMING PRIMARY SCHOOL PUPILS’ INFORMATION AND COMMUNICATIONS COMPETENCE WHILE STUDYING MATHEMATICS
Lyfenko A.V. (Asylyf@yandex.ru)
Tsyolkovsky Kaluga State Teachers’ Training University, Kaluga
Korkina L.N. (korkinaln@yandex.ru)
Kaluga Region Institute of Educationalists’ Professional Development, Kaluga
Abstract
The article covers the examples illustrating the ways of forming primary school pupils’ information and communications competence while studying mathematics.
ФОРМИРОВАНИЕ ИКТ-КОМПЕТЕНТНОСТИ УЧАЩИХСЯ НАЧАЛЬНОЙ ШКОЛЫ В ПРОЦЕССЕ ИЗУЧЕНИЯ МАТЕМАТИКИ
Лыфенко А.В. (Asylyf@yandex.ru)
Калужский государственный педагогический университет имени К.Э. Циолковского (КГПУ)
Коркина Л.Н. (korkinaln@yandex.ru)
Калужский областной институт повышения квалификации работников образования (КОИПКРО)
Аннотация
В статье приводятся примеры, которые показывают способы формирования ИКТ-компетентности учащихся начальных классов в процессе изучения математики.
Начальная школа является фундаментом всего последующего образования, поэтому в Государственном образовательном стандарте начального общего образования общеучебные умения указаны как обязательные для овладения всеми учащимися. Кроме того, в стандарте говорится о развитии личностных качеств и способностей младших школьников на основе приобретения ими опыта разнообразной деятельности: учебно-познавательной, практической, социальной, то есть стандарт общего образования нацелен на формирование у учащихся общих способов деятельности и умения конкретизировать обобщенные умения применительно к частным задачам, таким образом, стандарт базируется на компетентностном подходе.
В настоящей статье компетентность мы рассматриваем как совокупность знаний, умений и навыков в отношении к реальным объектам и процессам, а также готовность и способность их применять.
При конструировании содержания образования выделяют ключевые, компетентности, которые имеют надпредметный или межпредметный характер. Поскольку процесс обучения связан с передачей и получением информации, ее обработкой, и оценкой, то можно заключить, что эффективность процесса обучения зависит от сформированности у обучаемых ИКТ-компетености.
Рассматривая содержание понятия «ИКТ-компетентность», уровни и этапы формирования ИКТ-компетености, многие авторы указывают на необходимость формирования в первую очередь технических умений и навыков, связанных с умением использовать ПК для решения конкретной задачи. Таким образом, процесс формирования ИКТ-компетентностей у школьников начинается при изучении информатики и ИКТ.
На наш взгляд, начинать нужно с формирования информационных умений в процессе изучения других дисциплин. Школьника необходимо научить решать информационные задачи сначала без использования дополнительных технических устройств, опустив информационные процессы до уровня понятных ученику предметных действий, в противном случае нарушается поэтапность формирования информационных умений и способов действий, лежащих в основе ИКТ-компетентностей.
В начальном курсе математики, на наш взгляд, есть потенциал для формирования на пропедевтическом уровне ИКТ-компетентности. Например, при изучении математики рассматриваются различные виды треугольников по количеству равных сторон (разносторонние, равнобедренные, равносторонние) и величине углов (остроугольные, прямоугольные и тупоугольные). При обобщении видов треугольников структурирование информации может выступать в качестве средства для получения новой информации об объекте. Для этого достаточно на уроке построить таблицу 4х4, в которой в названиях строк и столбцов указать виды треугольников по различным классификациям. В ячейках таблицы могут быть изображены треугольники каждого из возможных видов, причем важно показать учащимся, что такой способ организации информации позволяет показать, что не может быть прямоугольного равностороннего треугольника и тупоугольного равностороннего треугольника. Таким образом, организация информации позволяет получить новую информацию, значимую в контексте изучаемого предмета, в данном случае математики.
ИКТ-компетентность школьника включает в себя умение собирать и интерпретировать информацию для различных параметров конкретной ситуации. Эта ситуация может быть задана в начальном курсе математики текстовой задачей, причем изменяемые параметры могут быть выражены как числовыми данными, так и отношениями. Например, после решения задачи «Пять участников соревнования стали его призерами, набрав по 20, 19, и 18 очков, заняв, соответственно первое, второе и третье места. Сколько участников завоевали каждое призовое место, если вместе они набрали 94 очка?» арифметическим методом можно предложить ученикам решить эту же задачу, изменив в ней числовые данные или некоторые отношения и предметную область. Вторая задача может быть следующей «В магазин привезли пять ящиков конфет по 20 кг, 19 кг и 18 кг в каждом. Сколько ящиков каждого вида привезли в магазин, если масса всех конфет 94 кг?». Сравнение условий и решения задач, которое за отсутствием места мы опускаем, приводит к выводу о возможности существования нескольких различных ответов во второй задаче. С точки зрения целей формирования ИКТ-компетентности важен не только факт наличия других ответов, но и технология их поиска. Для организации поиска решения целесообразно структурировать и упорядочить информацию, представленную в условии, и простейшие следствия из него в виде таблицы, в которую будут занесены значения произведений чисел 20, 19 и 18 на первые натуральные числа. Решение в таком случае сводится к составлению различных сумм из выписанных произведений, при этом задача, не теряя своего эвристического характера, становится отчасти алгоритмической.
К сожалению, рамки публикации не позволяют подробно рассмотреть названные выше примеры. Но они показывают, в каком направлении может осуществляться формирование ИКТ-компетентности младших школьников в процессе изучения математики.
КОМПЬЮТЕР В ОПЫТАХ СО ЗВУКОВЫМИ ИМПУЛЬСАМИ
Майер Р.В. (robert_maier@mail.ru)
Глазовский государственный педагогический институт
Аннотация
Экспериментальная установка состоит из компьютера, к которому подключены динамик и микрофон. Динамик преобразует поступающие от ПК сигналы в звуковые импульсы, сигнал с микрофона выводится на экран монитора. По времени запаздывания сигнала с микрофона можно определить его координату. Приведена программа на языке Pascal, управляющая динамиком и обрабатывающая сигнал со звуковой платы.
Для демонстрации распространения звуковых импульсов используется экспериментальная установка, состоящая из компьютера 4, к LPT––порту которого подключены активные колонки 1 с динамиком 2, а к входу звуковой платы –– микрофон 3 (рис. 1). Компьютер посылает импульс напряжения на колонки и начинает оцифровывать сигнал с микрофона, записывая его в массив. Затем он выводит осциллограмму на экран и все повторяется снова. При приближении микрофона к динамику осциллограмма смещается влево, а при удалении –– вправо. Параметры используемого ПК: Intel Celeron, 416 МГц, операционная система Windows 98 SE, звуковая плата ES1868 Plug and Play AudioDrive, диапазон ввода-вывода: 0220-022F. Перед запуском программ требуется отключить драйвер звуковой платы: Мой компьютер ––> Панель управления ––> Система ––> Устройства ––> ES1868 Plug and Play AudioDrive (WDM). Выбрать "Свойства", поставить галочку в опции "Отключено в данной конфигурации" и перезагрузить ПК. Интерфейс звуковой платы отключать не следует. Управление колонками и обработка сигнала с микрофона осуществляются программой 1.
С помощью оператора port[$378]:=255; (или 0) осуществляется подача логической 1 (или 0) на 2-9 выводы LPT–порта. К одному из них через резистор 1 кОм или конденсатор 10 мкФ следует подключить вход активных колонок. Программирование звуковой платы состоит в записи команды 20h (команда ввода 1 байта данных) в ячейку 22Ch с помощью оператора port[$22C]:=$20;. Операторы port[$226]:=1; port[$226]:=0; используются для сброса цифрового сигнального процессора [1, с.360–364] и обеспечения правильной работы звуковой карты. Результат оцифровки входного сигнала считывается оператором port[$22A]; и сохраняется в массиве x[i]. Когда на входе 0 В, x[i]=127. После заполнения всего массива либо одновременно с этим осуществляется построение графика на экране компьютера. Можно обойтись без звуковой платы, для этого сигнал с микрофона необходимо усилить и подать на один из выводов шины передачи данных LPT––порта (10––17 выводы). Их состоянию соответствует содержимое ячейки ОЗУ с адресом 379h, которое может быть считано оператором x[i]:=port[$379];. Звуковой сигнал, дойдя до микрофона, вызывает появление на соответствующем выводе LPT––порта логической 1. Это используется для изображения прямоугольного импульса на мониторе, определения времени запаздывания сигнала с микрофона по отношению к щелчкам динамика, нахождения расстояния между динамиком и микрофоном.
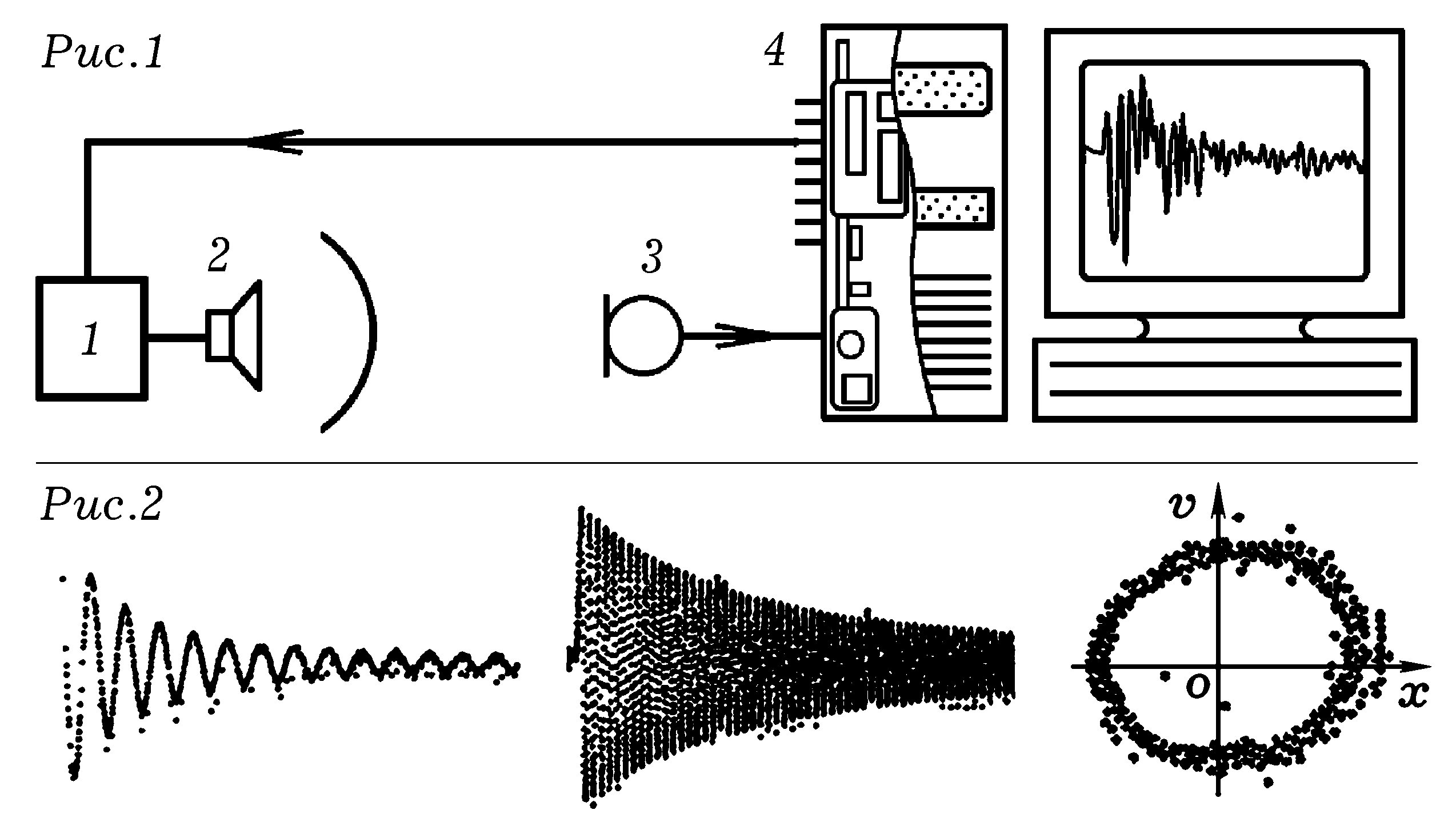
Рассмотренные опыты могут быть положены в основу акустического метода измерения координаты микрофона, установленного, например, на движущемся теле. Измерения осуществляются с точностью до 3–5 мм и периодичностью 0,4 с, результаты обрабатываются и выводятся на экран. Если микрофон установить на колеблющемся маятнике, то можно получить графики колебаний и фазовый портрет (рис.2). Автор благодарит Акатова Р.В., который 10 лет назад продемонстрировал ему аналогичный эксперимент на компьютере ZX Spectrum.
uses crt, graph; const n=320; m=5; {Программа 1.}
var Gd, Gm, i, z : integer; x : array [0..N] of integer;
BEGIN Gd:=Detect; InitGraph(Gd,Gm, 'c:\bp\bgi');
if graphResult <> grOk then Halt(1);
port[$226]:=1; delay(10); port[$226]:=0;
repeat port[$378]:=255; delay(1); port[$378]:=0;
for i:=1 to n do begin
port[$22C]:=$20; x[i]:=(port[$22A]-127)*2;
delay(1); end;
for i:=1 to n do begin
line(m*i,240-x[i],m*(i-1),240-z); z:=x[i];
end; delay(3000); cleardevice;
until KeyPressed;
END.
Предложенная демонстрация может быть использована при изучении общего и экспериментального курса физики, а также при рассмотрении физических принципов сбора и обработки информации.
Литература
1. Матаев Г.Г. Компьютерная лаборатория в вузе и школе. Учебное пособие. –– М.: Горячая линия–Телеком, 2004. –– 440 с.
2. Web–сайт glazov.net (электронный ресурс).
using of the practice computer games on the lessons
Makarova N.N. (natnik.7771@mail.ru)
Moscow Pedagogical State University (MPGU)
Abstract
The Practice computer games have a big spectrum of the possibilities for enabling students in active educational process. Modern children master the achievements of information-computer technology with interest and successfully. Consequently, using of the practice computer games on the lessons is supposed the activation of cognitive activity.
ИСПОЛЬЗОВАНИЕ УЧЕБНЫХ КОМПЬЮТЕРНЫХ ИГР НА УРОКАХ В НАЧАЛЬНОЙ ШКОЛЕ
Макарова Н.Н. (natnik.7771@mail.ru)
Московский Педагогический Государственный Университет (МПГУ)
Аннотация
Учебные компьютерные игры имеют большой спектр возможностей для включения учащихся в активный образовательный процесс. Современные дети с интересом и успешно осваивают достижения информационно-компьютерных технологий. Следовательно, использование учебных компьютерных игр на уроках предполагает активизацию познавательной деятельности.
Активное развитие новых информационных технологий и внедрение их в повседневную жизнь наложили определенный отпечаток на развитие личности современного ребенка. Мощный поток новой информации, рекламы, применение компьютерных технологий в телевидении, распространение игровых приставок, электронных игрушек и компьютеров оказывают большое влияние на воспитание ребенка и его восприятие окружающего мира.
Существенно изменяется и характер его любимой практической деятельности – игры, изменяются и его любимые герои и увлечения. Такого рода игры и увлечения можно использовать на уроках как средство включения детей в учебную деятельность, средство развития любознательности, метод изменения позиции пассивных детей, активизации учебного процесса.
На уроках игра объединяет познавательную и творческую активность. Игровая форма помогает детям включиться в познавательную деятельность, дает возможность многостороннего раскрытия личности, развития ее способностей, сплачивает учащихся. Разумное сочетание игровой занимательности и серьезности заданий помогает детям заниматься с интересом, быть активными и внимательными. Игровая деятельность способствует усвоению норм взаимопомощи, помогает сформировать адекватную самооценку.
Современные достижения в развитии информационной и компьютерной техники диктуют необходимость применения учебных компьютерных игр в образовательном процессе. Такие игры привлекают нынешних детей и способствуют формированию познавательной активности и навыков общения.
Литература
1. Варченко В.И. «Радуга в компьютере. Компьютерные игры в школе» (журнал Начальная школа №10 1997 стр.92-94)
2. Грамолин В.В. «Обучающие компьютерные игры» (журнал Информатика и образование №4 1994 стр.56-60)
3. Ладыженская Н.В. «Технические средства обучения на уроках риторики в школе» (коллективная монография Школа профессора Т.А.Ладыженской Москва Изд-во Прометей МПГУ 2005 244с. стр.195-198)
FEATURES OF VERIFICATION OF PROBLEMS IN COURCE OF CHEMISTRY BASED ON CHEMICAL ELEMENTS AND THEM PROPERTIES
Mantserov D.I. (mdi82@mail.ru)
Saint-Petersburg State University,
faculty of mathematics and mechanics, post-graduate student
ОСОБЕННОСТИ ВЕРИФИКАЦИИ ЗАДАЧ ПО КУРСУ ХИМИИ НА БАЗАХ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ И ИХ СВОЙСТВ
Манцеров Д.И.(mdi82@mail.ru)
Санкт-Петербургский Государственный Университет, математико-механический факультет
Аннотация
Ниже будет рассказано об особенностях проверки задач по курсу химии при помощи программы KVerifier. В качестве основы для проверки задач берутся химические элементы и их числовые характеристики(например: номер элемента, номер группы, валентность). Также несколько слов будет сказано о связи применение математического языка к решению задач по химии.
Среда KVerifier изначально была разработана для проверки знаний респондента. Первоначальная (существующая и работающая) версия предполагала проверку знаний в некоторых областях математики, такие как квадратичные уравнения, задачи на тему «четырехугольники», задачи на тему «треугольники». Со временем среда KVerifier была усовершенствована, и был разработан модуль для решения задач по химии. Данная представляет собой апплет, написанный на языке программирования JAVA. Данный апплет используется на web-странице, что позволяет его использовать через Internet. Эта возможность позволит использовать среду KVerifier для дистанционного обучения.
Особенность некоторых задач по химии состоит в том, что в качестве ответа требуют числовые характеристики элементов. В качестве таких характеристик выступают номер группы элемента, период элемента, валентность, порядковый номер, относительная атомная масса элемента и т.д.
В основе проверки правильности ответа в среде лежит метод проверки истинности предикатов. Процесс проверки истинности гипотезы основан на проверке истинности выражений, которые содержат знаки бинарных и унарных логических операций (логическое И, логическое ИЛИ, импликация и другие). Анализ таких операций проходит согласно их старшинству.
В базе данных химических элементов в среде KVerifier каждый элемент имеет логические утверждения, которые либо истинны, либо ложны для данного примера. При проверке гипотезы, введенной учеником, среда проверяет эту гипотезу на значениях логических утверждениях примеров. Логическое утверждение для каждого элемента – это либо одно из значений числовых характеристик, либо связанные между собой при помощи логических операций числовые характеристики элемента.
Каждая числовая характеристика химического элемента в среде представлена переменной. Ответ вводится при помощи переменных и логических операций с переменными.
Данная среда позволяет не только проверять знания, но и позволяет поддерживать исследовательской деятельности учащегося школьных заведений в процессе решения задач по химии. Используя возможность работы с базами примеров, среда осуществляет экспертизу произвольных утверждений учащихся на обширном числе примеров химических элементов, на которых гипотезы (введенный ответ) не выполняются, так и те, которые подтверждают гипотезу. Поэтому среду следует рассматривать как средство поддержки самостоятельной (в том числе, исследовательской) деятельности респондента в рамках курса химии.
Благодаря наличию количественных характеристик химических элементов, задачи, связанные с их поиском, могут быть интерпретированы задачи, для решения которых потребуется использование математического аппарата и языка логики.
В дальнейшем планируется найти связи между математикой и другими науками. Эти связи планируется отобразить в среде KVerifier.
Литература
1. Башмаков М.И., Поздняков С.Н., Резник Н.А. Информационная среда обучения. - СПб.: Свет, 1995.
2. Иванов С.Г. Компьютерная поддержка решения математических задач как способ организации продуктивной деятельности учащихся. Диссертация на соискание ученой степени кандидата педагогических наук. - Москва, 2004.
3. Дж. Пойа Математическое открытие. – Москва, Главная редакция физико-математической литературы. Издание второе, стереотипное. Перевод В.С. Бермана. Издательство «Книга», 1976.
4. Pozdnyakov S. Mathematical models of intellectual dialogue in Computer Aided Learning. World Conference on Twenty-First Century Mathematics. Proseedings. School of Mathematical Sciences, GC University, Lahore, Punjab (Pakistan), 2005.
