Вавилова закон

Вид материала

Закон

Содержание Власова уравнение Внесистемные единицы Внешнее трение Внутреннее трение Внутренняя энергия Т0 В. э. конденсированных систем (жид­ких и тв. тел) приближается к определ. пост. значению U Внутрикристаллическое по­ле Водородная связь Водородный термометр Водородоподобные атомы Возбуждённая проводимость Возбуждённое состояние Возможные перемещения Возможных перемещений принцип Возмущений теория Шрёдингера уравнения Фейнмана диаграммами). В. И. Григорьев.

Подобный материал:

• Н. И. Вавилова аналитический отчет, 217.51kb.
• Урок по общей биологии в 11 классе «Дело академика Вавилова», 851.64kb.
• Селекция- одомашнивание, 126.51kb.
• Уважаемые коллеги!, 64.43kb.
• Українське товариство генетиків І селекціонерів ім. М.І. Вавилова, 45.97kb.
• «Саратовский государственный аграрный университет имени Н. И. Вавилова», 377.27kb.
• Саратовский Государственный Аграрный Университет им. Н. И. Вавилова. Кафедра Акушерства, 248.61kb.
• О. Б. Ширяев Институт общей физики ран, 119991, Москва, ул. Вавилова,, 20.28kb.
• Главное управление образования, 70.84kb.
• Издательский дом, 529.99kb.

ВИЦИНАЛЬ (от лат. vicinus — сосед­ний, близкий), побочная грань крис­талла, слабо отклонённая от к.-л. из осн. граней кристалла на малый (5°) угол. Поверхность В. представ­ляет собой лестницу из ступеней вы­сотой порядка долей или единиц пара­метров элементарной ячейки крис­талла, чередующихся с террасами, образованными участками осн. гра­ни. На каждой грани кристалла в про­цессе его роста может возникать по 2, 3, 4, 6 (в зависимости от точечной группы симметрии кристалла) В., наклонённых в разные стороны, но симметрически связанных и образую­щих пологие пирамидальные холмики. На одной грани может быть неск. вицинальных холмиков роста (рис.). Наклон В. роста определяется усло­виями кристаллизации. При раство­рении кристаллов образуются вицинальные ямки. Иногда В. обнаруживаются на поверхности скола.




ВЛАСОВА УРАВНЕНИЕ, кинетич. ур-ние (типа кинетического уравнения Больцмана) для бесстолкновительноц плазмы. См. Плазма.

ВМОРОЖЕННОСТЬ МАГНИТНОГО ПОЛЯ, см. Магнитная гидродина­мика.

ВНЕСИСТЕМНЫЕ ЕДИНИЦЫ, еди­ницы физ. величин, не входящие ни в одну из существующих систем еди­ниц. В. е. можно разделить на неза­висимые (определяемые без помощи других единиц, напр. градус Цельсия, бел) и произвольно выбранные, но выражаемые нек-рым числом других единиц (напр., атмосфера, лошадиная сила, световой год, парсек).

ВНЕШНЕЕ ТРЕНИЕ, см. Трение внешнее.

ВНУТРЕННЕЕ ТРЕНИЕ в твёрдых телах, свойство твёрдых тел необра­тимо превращать в теплоту механич. энергию, сообщённую телу в процессе его деформирования. В. т. связана с двумя разл. группами явлений — неупругостью и пластич. деформацией. Неупругость представляет собой отклонение от св-в упругости при деформировании тела в условиях, когда остаточные деформации практи­чески отсутствуют. При деформиро­вании с конечной скоростью в теле возникает отклонение от теплового равновесия. Напр., при изгибе равно­мерно нагретой тонкой пластинки, материал к-рой расширяется при на­гревании, растянутые волокна охла­дятся, сжатые — нагреются, вследст­вие чего возникает поперечный пере­пад темп-ры, т. е. упругое деформи­рование вызовет нарушение теплового равновесия. Последующее выравни­вание темп-ры путём теплопровод-

79


ности представляет собой процесс, сопровождаемый необратимым пере­ходом части упругой энергии в теп­лоту (т. н. релаксац. процесс — см. Релаксация). Этим объясняется на­блюдаемое на опыте затухание сво­бодных изгибных колебаний пластин­ки — т. н. термоупругий эф­фект.

При упругом деформировании спла­ва с равномерным распределением ато­мов разл. компонентов может про­изойти перераспределение атомов в в-ве, связанное с различием их разме­ров. Восстановление равновесного распределения атомов путём диффузии также представляет собой релаксац. процесс. Проявлениями неупругих, или релаксационных, св-в, кроме упо­мянутых, явл. упругое последействие в чистых металлах и сплавах, упру­гий гистерезис и др.

Деформация, возникающая в упру­гом теле, зависит не только от при­ложенных к нему внешних механич. сил, но и от темп-ры тела, его хим. состава, внешних магн. и электрич. полей (магнито- и электрострикция), величины зерна, его крист. структуры и т. д. Это приводит к многообразию релаксац. явлений, каждое из к-рых вносит свой вклад в В. т. Если в теле одновременно происходит неск. ре­лаксац. процессов, каждый из к-рых можно характеризовать своим време­нем релаксации _i то совокупность всех времён релаксации отдельных ре­лаксац. процессов образует т.н. релак­сац. спектр этого материала, характе­ризующий его при данных условиях; каждое структурное изменение в об­разце меняет релаксац. спектр.

Величину В. т. измеряют по зату­ханию свободных колебаний (продоль­ных, поперечных, крутильных, изгиб­ных), по резонансной кривой для вы­нужденных колебаний, по относит. рассеянию упругой энергии за один период колебаний. В. т. явл. источни­ком сведений о процессах, возникаю­щих в тв. телах, в частности в чистых металлах и сплавах, подвергнутых разл. механич. и тепловым обработ­кам.

В. т. при пластической деформации. Если силы, дей­ствующие на тв. тело, превосходят предел упругости и возникает пластич. течение, то можно говорить о квазивязком сопротивлении течению (по аналогии с вязкой жидкостью), со­провождающимся превращением ме­ханич. энергии в теплоту. Механизм В. т. при пластич. деформации су­щественно отличается от механизма В. т. при неупругости (см. Пластич­ность, Ползучесть материалов). Раз­личие в механизмах рассеяния энер­гии определяет разницу в значениях вязкости, отличающихся на 5—7 по­рядков (вязкость пластич. течения, достигающая величины 10¹³—10¹⁵ Па•с.

всегда значительно выше вязкости, вычисляемой из упругих колебаний и равной 10⁷—10⁸ Па•с). По мере роста амплитуды упругих колебаний всё большую роль начинают играть плас­тич. сдвиги, и величина вязкости рас­тёт, приближаясь к значениям вяз­кости пластич. течения.

ВНУТРЕННЕЕ ТРЕНИЕ в жидкостях и газах, то же, что вязкость.

ВНУТРЕННЯЯ ЧЕТНОСТЬ (Р), одна из хар-к (квант. чисел) элем. ч-цы, определяющая поведение её волновой функции  при пространственной ин­версии (зеркальном отражении), т. е. при замене координат х-х, y-у, z-z. Если при таком отражении  не меняет знака, В. ч. ч-цы положи­тельна (Р=+1), если меняет — отри­цательна (Р=-1). Для бозонов В. ч. ч-цы и античастицы одинаковы, для фермионов произведение В. ч. ч-цы и античастицы равно -1. См. также Чётность.

ВНУТРЕННЯЯ ЭНЕРГИЯ, энергия физ. системы, зависящая от её внутр. состояния. В. э. включает энергию хаотического (теплового) движения всех микрочастиц системы (молекул, атомов, ионов и т. д.) и энергию вз-ствия этих ч-ц. Кинетич. энергия движения системы как целого и её потенц. энергия во внеш. силовых полях в В. э. не входят. В термодинамике и её приложениях представляет инте­рес не само значение В. э. системы, а её изменение при изменении состоя­ния системы. Поэтому обычно при­нимают во внимание только те со­ставляющие В. э., к-рые изменяются в рассматриваемых процессах изме­нения состояния в-ва. , Понятие «В. э.» ввёл в 1851 англ. учёный У. Томсон (лорд Кельвин), определив изменение В. э. (U) физ. системы в к.-н. процессе как алгебр. сумму количеств теплоты Q, к-рыми система обменивается в ходе процесса с окружающей средой, и работы А, совершённой системой или произведён­ной над ней:

U=Q+A. (*)

Принято считать работу положитель­ной, если она производится системой над внеш. телами, а кол-во теплоты положительным, если оно передаётся системе. Ур-ние (*) выражает первое начало термодинамики — закон со­хранения энергии в применении к про­цессам, в к-рых происходит передача теплоты. Согласно закону сохранения энергии, В. э. явл. однозначной ф-цией состояния физ. системы, т. е. одно­значной ф-цией независимых перемен­ных, определяющих это состояние, напр. темп-ры Т и объёма V (или дав­ления р). Однозначность В. э. при­водит к тому, что, хотя каждая из величин Q и А зависит от хар-ра про­цесса, переводящего систему из со­стояния с В. э. U₁ в состояние с энер­гией U₂, изменение U определяется лишь значениями В. э. в нач. и кон. состояниях: U=U₂-U₁. Для любого замкнутого процесса, возвра­щающего систему в первонач. состо­яние (U₂=U₁), изменение В. э. равно нулю и Q=A (см. Круговой процесс). Изменение В. э. системы в адиабати­ческом процессе (т. е. при Q=0) равно работе, производимой над системой или произведённой системой: U=A _ад. В случае простейшей физ. системы с малым межмол. вз-ствием — идеаль­ного газа — изменение В. э. сводится к изменению кинетич. энергии молекул:

U=Мс_VТ,

где М — масса газа, c_V — уд. тепло­ёмкость при пост. объёме. . Поэтому U для идеального газа опреде­ляется только изменением темп-ры Т (закон Джоуля). В физ. системах, ч-цы к-рых взаимодействуют между собой (реальные газы, жидкости, тв. тела), В. э. включает также энергию межмол. и внутримол. вз-ствий. В. э. таких систем зависит как от темп-ры, так и от давления (объёма).

Экспериментально может быть из­мерено только изменение В. э. в к.-л. физ. процессе, то есть В. э. опреде­ляется с точностью до пост, слагае­мого. Методы статистической физики позволяют в принципе теоретически рассчитать В. э. физ. системы, но так­же лишь с точностью до пост. слагае­мого, зависящего от выбранного нуля отсчёта.

В области низких темп-р при Т0 В. э. конденсированных систем (жид­ких и тв. тел) приближается к определ. пост. значению U₀ (см. Третье на­чало термодинамики). Значение U₀ мо­жет быть принято за начало отсчёта В. э.

В. э. явл. термодинамич. потенциа­лом (как ф-ция энтропии S и объёма V), дифференцированием U по S и V можно определить ряд других пара­метров системы.

• См. лит. при ст. Потенциалы термоди­намические.

А. А. Лопаткин.

ВНУТРИКРИСТАЛЛИЧЕСКОЕ ПО­ЛЕ, электрич. поле, существующее внутри кристаллов вследствие того, что на коротких (порядка межатом­ных) расстояниях поля, создаваемые положит. и отрицат. зарядами, не скомпенсированы. Реже В. п. назы­ваются также существующие внутри нек-рых кристаллов магн. поля. Для расчётов электрич. В. п. часто поль­зуются приближением точечных за­рядов и диполей — ионы и молекулы, обладающие дипольным моментом, рассматриваются как точечные заря­ды или электрич. диполи, находящи­еся в узлах крист. решётки. В. п. мо­гут достигать напряжённости 10⁸ В/см и более. Симметрия В. п. определяется гл. обр. симметрией кристалла. Ве­личина и симметрия В. п. в данной точке кристалла зависит от деформа­ций, от наличия примесей, дефектов и от поляризации кристалла. В. п. непрерывно колеблется в небольших пределах относительно своего ср. зна­чения благодаря колебаниям кристал-

80


лической решётки. Экспериментально электрич. В. п. исследуются опти­ческими и радиоспектроскопическими методами.

Значительные магн. поля возни­кают в кристаллах, содержащих парамагн. атомы. Они создают магн. поле, убывающее обратно пропорц. кубу расстояния от них (магн. ди­поли). Напр., магн. момент атомов переходных элементов создаёт в ок­ружающем пр-ве (на расстояниях по­рядка межатомных) магн. поля, до­стигающие напряжённости магн. поля тысяч и даже десятков тысяч Э. Осо­бый интерес представляют поля, со­здаваемые эл-нами на «собственном» ат. ядре, к-рые исследуются мето­дами, основанными на ядерном магн. резонансе и Мёссбауэра эффекте.

• Бальхаузен К., Введение в теорию поля лигандов, пер. с англ., М., 1964. См. также лит. при ст. Ядерный магнитный ре­зонанс и Мёссбауэра эффект.

ВОДОРОДНАЯ СВЯЗЬ, тип связи, промежуточный между ковалентной химической связью и невалентным межат. вз-ствием и осуществляющийся с участием атома водорода, располо­женного либо между молекулами, либо между атомами внутри моле­кулы. Примером межмолекулярной В. с. явл. связь между молекулами

воды:



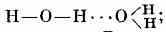
внутри- и

межмолекулярные В. с. типа N—Н•••О часто встречаются в бпополимерах — белках, нуклеиновых кислотах и пр. В. с. объясняется тем, что эл-н атома водорода слабо связан с прото­ном и легко смещается к электроотрицат. атому, напр. к ближайшему атому кислорода или азота. В резуль­тате протон почти «оголяется», и со­здаются условия для сближения ато­мов О•••О или N•••O. См. также Межатомное взаимодействие.

В. Г. Дашевский.

ВОДОРОДНЫЙ ТЕРМОМЕТР, см. Газовый термометр.

ВОДОРОДНЫЙ ЦИКЛ (протон-про­тонный цикл), последовательность термоядерных реакций в звёздах, при­водящая к превращению водорода в ге­лий без участия катализаторов. В. ц.— осн. источник энергии норм. одно­родных звёзд, в частности Солнца. Последовательность реакций В. ц. приведена в табл. 2 ст. Термоядерные реакции.

ВОДОРОДОПОДОБНЫЕ АТОМЫ, атом Н и ионы, состоящие из ядра и одного эл-на (Не⁺ , Li²⁺ , Ве³⁺ , . . .). Обладают сходными оптич. св-вами (см. Атом). В физике полупроводников В. а. наз. примесные атомы, у к-рых валентность на единицу больше или меньше, чем у атомов осн. в-ва полу­проводника.

ВОЗБУЖДЕНИЕ атома или молекулы, переход атома или молекулы из ос­новного состояния в состояние с боль­шей энергией (на один из вышележа­щих уровней энергии). В. происходит при столкновениях ч-ц (см. Столкно­вения атомные) или при вз-ствии ч-цы

с квантами эл.-магн. излучения (как правило, в тех случаях, когда энергия, получаемая ею в акте вз-ствия, недостаточна для её ионизации). Вся­кое состояние атома или молекулы, кроме основного, наз. возбуждённым состоянием; каждое из них характе­ризуется определ. кол-вом энергии (энергией В.), к-рое ч-ца получает при переходе из основного в данное возбуждённое состояние. Если послед­нее не явл. метастабильным состо­янием, то после очень кратковрем. пребывания в нём (для атомов~10^-8 с) ч-ца самопроизвольно переходит в основное или др. состояние с мень­шей энергией. Ср. время существо­вания возбуждённого состояния наз. временем жизни ч-цы на уровне энер­гии. Атомы и молекулы в возбуждён­ных состояниях обычно значительно более химически активны, чем в ос­новном состоянии.

ВОЗБУЖДЁННАЯ ПРОВОДИМОСТЬ, увеличение электропроводности ди­электриков и полупроводников при ос­вещении (см. Фотопроводимость) или при электронной бомбардировке их поверхности (электронно-возбужденная проводимость). В. п. обусловлена генерацией элект­ронно-дырочных пар.

ВОЗБУЖДЁННОЕ СОСТОЯНИЕ кван­товой системы, состояние атома, мо­лекулы и др. квант. систем с энергией выше минимальной из дискр. ряда возможных для этой системы энергий. Возбуждёнными наз. все состояния, кроме основного состояния (состояния с мин. энергией). Для перехода сис­темы в В. с. её необходимо возбудить — сообщить ей энергию (см., напр., Возбуждение). В. с. обладают, как правило, конечными временами жиз­ни. Уровни энергии, соответствующие В. с., также наз. возбуждёнными.

ВОЗГОНКА (сублимация), переход в-ва из тв. состояния в газообразное, минуя жидкую фазу. ВОЗДУХ, смесь газов, из к-рых состо­ит атмосфера Земли (азот — 78,08%, кислород — 20,95%, инертные газы и водород — 0,94%, СO₂—0,03%, в небольших кол-вах O₃, CO, NH₃, CH₄, SO₂ и др.). Средняя мол. м.— ок. 29 атомных ед. При 0°С давление В. на ур. м. 101 325 Па (1 ат, или 760 мм рт. ст.). В этих, т. н. нормальных, условиях масса 1 л В. рав­на 1,2928 г; темп-pa кипения жидкого В. при норм. давлении — ок. 83 К. Показатель преломления 1,00029, диэлектрич. проницаемость 1,000059. Критич. темп-pa В.-140,7°С, критич. давление 3,7 МН/м².

Для большинства расчётов В. можно считать идеальным газом (отклонения св-в В. от св-в идеального газа ха­рактеризуется коэфф. сжимаемости, к-рый при 0°С равен 1,00060). Тепло­ёмкость, вязкость и теплопроводность В. в значит. степени зависят от давле­ния и темп-ры.

ВОЗДУШНЫЙ ТЕРМОМЕТР, см. Газовый термометр.

ВОЗМОЖНЫЕ ПЕРЕМЕЩЕНИЯ (вир­туальные перемещения), элементарные (бесконечно малые) перемещения, к-рые точки механич. системы могут совершать из занимаемого ими в дан­ный момент времени положения, не нарушая наложенных на систему свя­зей (см. Связи механические). В. п.— понятия чисто геометрические, не за­висящие от действующих сил; они определяются только видом наложен­ных на систему связей и вводятся как хар-ки этих связей, показывающие, какие перемещения при наложенных связях остаются для системы возмож­ными. Напр., если связью для точки явл. к.-н. поверх­ность и точка нахо­дится на ней в дан­ный момент в по­ложении М (рис.),



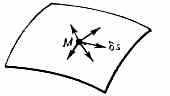
то В. п. точки в этот момент будут элем. отрезки (векторы) длиной s, направленные по касатель­ной к поверхности в точке М. Переме­щение по любому другому направле­нию не будет В. п., т. к. при этом нарушится связь (точка не останется на поверхности). Понятие «В. п.» от­носится и к покоящейся и к движу­щейся точке. Если связь со временем не изменяется, то истинное элем. перемещение ds движущейся точки из положения М совпадает с одним из В. п.

Понятием «В. п.» пользуются для определения условий равновесия и ур-ний движения механич. системы (см. Возможных перемещений принцип, Д'Аламбера — Лагранжа принцип), а также при нахождении числа степе­ней свободы системы.

С. М. Тарг.

ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ ПРИНЦИП, один из вариационных принципов механики, устанавливаю­щий общее условие равновесия меха­нич. системы. Согласно В. п. п., для равновесия механич. системы с иде­альными связями (см. Связи механи­ческие) необходимо и достаточно, чтобы сумма работ A_i всех приложенных к системе активных сил на любом возможном перемещении системы была равна нулю. Математически В. п. п. выражается ур-нием:

A_iF_is_icos_i=0, (*)

где f_i — действующие активные силы, 6s; — величины возможных переме­щений точек приложения этих сил, _i — углы между направлениями сил и возможных перемещений. Для сис­тем с неск. степенями свободы ур-ние (*) может составляться для каждого независимого перемещения в отдель­ности. В. п. п. позволяет найти ус­ловия равновесия системы с идеаль­ными связями, не вводя неизвестных реакций связей, что существенно уп­рощает решение и расширяет класс разрешимых задач. О применении метода, аналогичного даваемому


81


В. п. п. к решению задач динамики,

см. Д'Аламбера — Лагранжа прин­цип.

С. М. Тарг.

ВОЗМУЩЕНИЙ ТЕОРИЯ, метод приб­лижённого решения ур-ний, содержа­щих к.-л. малые параметры; в ур-ннях, описывающих физ. системы, В. т. ис­пользуется в тех случаях, когда нек­рое воздействие на эту систему (воз­мущение) может считаться малым.

Метод В. т. состоит в том, что сна­чала находится более простое реше­ние для «невозмущённой» системы, а затем с помощью этого решения вы­числяются поправки, вносимые воз­мущением. «Подправленное» решение можно использовать для нахождения след. поправки и т. д. Таким обра­зом, В. т. сводится к последователь­ному, поэтапному уточнению решения (отсюда другое назв. В. т.— метод последовательных при­ближений). Решение получается в виде ряда по степеням нек-рой без­размерной величины, характеризую­щей возмущение. Когда возмущение действительно мало, каждый после­дующий член данного ряда много меньше предыдущего, и поэтому можно ограничиться лишь первыми членами ряда (первыми поправками).

Исторически В. т. первоначально применялась в небесной механике для приближённого решения трёх тел задачи. Здесь роль невозмущённой за­дачи играет кеплерова задача для двух тел. Возмущение, вызываемое движением третьего тела, считается малым и описывается малыми чле­нами ур-ний движения.

В. т. явл. одним из важных мето­дов решения осн. ур-ния квант. ме­ханики — Шрёдингера уравнения и применяется во всех случаях, когда вз-ствие можно разбить на две части: основную, почти полностью опреде­ляющую состояние системы, и отно­сительно менее существенную (воз­мущение), приводящую лишь к незначит. изменению этого состояния. Напр., решая задачу об атоме водо­рода, помещённом во внеш. электрич. поле (Штарка эффект), напряжён­ность к-рого много меньше напряжён­ности кулоновского поля ядра (в пре­делах атома), сначала пренебрегают воздействием внеш. поля, т. е. нахо­дят волн. ф-ции, уровни энергии и др. физ. величины для невозмущёиного атома, затем, используя «невозму­щённые» волн. ф-ции, находят поправ­ки к уровням, обусловленные воздейст­вием внеш. поля. Иногда эту процеду­ру последоват. уточнения приходится проделывать неск. раз, подсчитывая поправки всё более высокого по­рядка.

Особое значение приобрела В. т. в квант. теории эл.-магн. поля (квант. электродинамике) для вычисления амплитуд разл. процессов. Способы точного решения ур-ний квант. теории

полей неизвестны. В то же время вы­числения по В. т. приводят в квант. электродинамике к результатам, пре­красно согласующимся с опытом.

В кач-ве примера рассмотрим задачу о вз-ствии электрон-позитронного по­ля с эл.-магн. полем. Само это вз-ст­вие будем считать малым возмуще­нием. В нулевом приближении, т. е. когда возмущение (вз-ствие полей) считается равным нулю, ч-цы, соот­ветствующие этим полям (эл-ны и позитроны, фотоны), явл. свободными; иными словами, всё выглядит так, как если бы электрич. заряды эл-нов и позитронов обратились в нуль (вз-ствие отсутствует). Первое при­ближение наглядно соответствует сле­дующему: все ч-цы движутся как свободные до нек-рой точки, в к-рой происходит их встреча и где в ре­зультате вз-ствия начальные ч-цы ис­чезают, а вместо них появляются но­вые ч-цы, к-рые от момента своего возникновения также движутся как свободные. Т. о., первое приближе­ние учитывает лишь один акт вз-ствия, точнее, один акт вызванных вз-ствием превращений ч-ц. В следующих — во втором, третьем и т. д. приближениях учитывается соотв. два, три и т. д. акта вз-ствия.

Описание вз-ствия эл-нов, позит­ронов и фотонов по В. т. можно изоб­разить графически (такие графики



наз. Фейнмана диаграммами). Напр., если свободный эл-н изображать сплошной, а фотон — волнистой ли­ниями, то в первом приближении (в первом порядке по В. т.) испуска­ние и поглощение фотона эл-ном да­ются графиками, изображёнными на рис. 1 и 2. (Реальные процессы такого типа запрещены, т. к. в них не вы­полняются одновременно законы со­хранения энергии и импульса.) Про­цесс рассеяния фотонов на эл-нах — Комптон эффект — связан минимум с двумя актами вз-ствия: актом ис­пускания и актом поглощения фото-



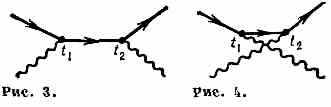
на эл-ном. Поэтому самый низкий порядок В. т., описывающий такой процесс, второй. Соответствующие гра­фики на рис. 3 и 4 отличаются лишь временной последовательностью ак­тов испускания и поглощения. График на рис. 3, напр., расшифровывается так: в нач. момент присутствует один эл-н и один фотон (причём каждая из ч-ц имеет определённые импульс, энергию, спин); в момент времени t₁ фотон поглощается эл-ном, и эл-н

переходит в новое состояние (или: исчезают обе нач. ч-цы, и возникает новая ч-ца — эл-н в отличном от начального, промежуточном, состоя­нии); в момент t₂ этот эл-н испускает новый (рассеянный) фотон и сам пере­ходит в кон. состояние (или: промежу­точный эл-н поглощается, а вместо него возникают кон. эл-н и новый фо­тон). Т. к. промежуточный эл-н су­ществует кон. время t₂-t₁, то появ­ляется квант. неопределённость энер­гии ξ~h/(t₂-t₁) (см. Неопределён­ностей соотношение), к-рая и сни­мает запрет на соответствующий каж­дой из «вершин» графика (точек, в к-рых осуществляется вз-ствие ч-ц) акт испускания или поглощения фо­тона.

При вычислении амплитуды про­цесса, отвечающего к.-л. графику, по всем t₁ и t₂>t₁ производится интег­рирование; это отражает тот факт, что вз-ствие с одинаковой вероятно­стью может произойти в любой мо­мент времени. Учёт каждого акта вз-ствия даёт вклад в амплитуду, пропорциональный электрич. заряду е. Поэтому разложение по В. т. можно назвать разложением по заряду. Ве­роятность процесса (равная квадрату модуля амплитуды процесса), к-рому отвечает график с n вершинами, пропорц. величине ⁿ, где =е²/hc¹/₁₃₇—постоянная тонкой структуры. Малость величины а по сравнению с единицей обычно рассматривается как аргумент, позволяющий отбрасывать высшие приближения В. т.

В. т. приводит к появлению беско­нечно больших значений для нек-рых физ. величин; для устранения этих бесконечностей в квант. электроди­намике разработан метод перенорми­ровок. Вопрос о суммировании всех членов ряда, даваемых В. т., остаётся пока открытым.

В. И. Григорьев.