Вавилова закон

Вид материала

Закон

Содержание Волновая механика Относительности теория) Волновая функция В. И. Григорьев. Волновод акустический Волновод оптический Волновое сопротивление Волновое сопротивление Волновое сопротивление Волновое уравнение Волновое число Волновой вектор Волновой пакет Расплывание волн. пакета о течением вре­мени t. В нач. момент времени ч-ца описы­вается волн. пакетом  В. И. Григорьев.

Подобный материал:

• Н. И. Вавилова аналитический отчет, 217.51kb.
• Урок по общей биологии в 11 классе «Дело академика Вавилова», 851.64kb.
• Селекция- одомашнивание, 126.51kb.
• Уважаемые коллеги!, 64.43kb.
• Українське товариство генетиків І селекціонерів ім. М.І. Вавилова, 45.97kb.
• «Саратовский государственный аграрный университет имени Н. И. Вавилова», 377.27kb.
• Саратовский Государственный Аграрный Университет им. Н. И. Вавилова. Кафедра Акушерства, 248.61kb.
• О. Б. Ширяев Институт общей физики ран, 119991, Москва, ул. Вавилова,, 20.28kb.
• Главное управление образования, 70.84kb.
• Издательский дом, 529.99kb.

ВОЛНОВАЯ МЕХАНИКА, то же, что квантовая механика.

ВОЛНОВАЯ ОПТИКА, раздел физ. оптики, изучающий совокупность яв­лений, в к-рых проявляется волн. природа света. Представления о волн. хар-ре распространения света восхо­дят к основополагающим работам голл. учёного 2-й пол. 17 в. X. Гюй­генса. Существ. развитие В. о. полу­чила в исследованиях Т. Юнга (Ве­ликобритания), О. Френеля, Д. Араго (Франция) и др., когда были прове­дены принципиальные опыты, по­зволившие не только наблюдать, но и объяснить явления интерференции света, дифракции света, измерить длину волны, установить поперечность световых колебаний и выявить другие особенности распространения световых волн. Но для согласования поперечности световых волн с осн. идеей В. о. о распространении упру­гих колебаний в изотропной среде пришлось наделить эту среду (миро­вой эфир) рядом трудносогласуемых между собой требований. Гл. часть этих затруднений была разрешена

82


в кон. 19 в. англ. физиком Дж. Мак­свеллом при анализе ур-ний, связы­вающих быстропеременные электрич. и магн. поля. В работах Максвелла была создана новая В. о.— эл.-магн. теория света, с помощью к-рой ока­залось совсем простым объяснение целого ряда явлений, напр. поляриза­ции света и количеств. соотношений при переходе света из одного прозрач­ного диэлектрика в другой (см. Фре­неля формулы). Применение эл.-магн. теории в разл. задачах В. о. показало согласие с экспериментом. Так, напр., было предсказано явление светового давления, существование к-рого было доказано П. Н. Лебедевым (1899). Дополнение эл.-магн. теории света модельными представлениями элект­ронной теории (см. Лоренца — Мак­свелла уравнения) позволило просто объяснить зависимость показателя преломления от длины волны (диспер­сию света) и др. эффекты.

Дальнейшее расширение границ В. о. произошло в результате приме­нения идей спец. теории относительности (см. Относительности теория), эксперим. обоснование к-рой было связано с тонкими оптич. опытами, в к-рых осн. роль играла относит. скорость источника и приёмника света (см. Майкелъсона опыт). Развитие этих представлений позволило исклю­чить из рассмотрения мировой эфир не только как среду, в к-рой распрост­раняются эл.-магн. волны, но и как абстрактную систему отсчёта.

Однако анализ опытных данных по равновесному тепловому излучению и фотоэффекту показал, что В. о. имеет определ. границы приложения. Рас­пределение энергии в спектре тепло­вого излучения удалось объяснить нем. физику М. Планку (1900), к-рый пришёл к заключению, что элемен­тарная колебат. система излучает и поглощает энергию не непрерывно, а порциями — квантами. Развитие А. Эйнштейном теории квантов при­вело к созданию физики фотонов — новой корпускулярной оптики, к-рая, дополняя эл.-магн. теорию света, пол­ностью соответствует общепризнан­ным представлениям о дуализме света.

Н. И. Калитеевский.

ВОЛНОВАЯ ФУНКЦИЯ в квантовой механике (амплитуда вероятности, век­тор состояния), величина, полностью описывающая состояние микрообъек­та (эл-на, протона, атома, молекулы) и вообще любой квант. системы.

Описание состояния микрообъекта с помощью В. ф. имеет статистиче­ский, т. е. вероятностный, хар-р: квад­рат В. ф. даёт значение вероятностей тех величин, от к-рых зависит В. ф. Напр., если задана зависимость В. ф.  ч-цы от её координат х, у, z и вре­мени t, то квадрат модуля В. ф. |(x, у, z, t)|² определяет вероятность нахождения ч-цы в момент времени t в точке с координатами х, у, z. По­скольку вероятность определяется квадратом , В. ф. называют также амплитудой вероятности. Исторически назв. «В. ф.» возникло из-за того, что ур-ние, определяющее эту ф-цию (Шрёдингера уравнение), похоже на ур-ние, описывающее волн. процессы. В. ф. описывает не только распреде­ление вероятностей нахождения мик­рообъекта в пр-ве, но и позволяет получать максимально полную, сов­местимую с принципами квант. меха­ники информацию о любых физ. величинах, характеризующих эти микрообъекты.

Для В. ф. справедлив суперпозиции принцип: если система может нахо­диться в разл. состояниях, описывае­мых В. ф. ₁, ₂, ... и т. д., то воз­можно и состояние с В. ф., равной сумме (и вообще любой линейной ком­бинации) этих В. ф. Сложение В. ф. (амплитуд вероятностей), а не вероят­ностей (квадратов В. ф.) принципи­ально отличает квант. теорию от лю­бой классич. статистич. теории, в к-рой для независимых событий спра­ведлива теорема сложения ве­роятностей.

Для системы из мн. одинаковых (тождественных) микрочастиц сущест­венны св-ва симметрии В. ф., опреде­ляющие статистику всего ансамбля ч-ц (см. Квантовая механика).

При описании объектов, являю­щихся частью (подсистемой) нек-рой большой системы — термостата, вмес­то В. ф., к-рая здесь не может быть введена, следует пользоваться матри­цей плотности (см. также Смешанное состояние).

В. И. Григорьев.

ВОЛНОВОД, устройство или канал в неоднородной среде, вдоль к-рого могут распространяться направлен­ные волны. Различают экранирован­ные В., образованные зеркально от­ражающими стенками (металлич. ра­диоволноводы и мн. типы акустич. волноводов), а также системы, в к-рых поперечная локализация волн обус­ловлена полным внутренним отраже­нием. Последние могут иметь как рез­кие (в масштабе длины волны Я) гра­ницы (диэлектрич. радиоволноводы, световоды), так и границы с плавными переходами к однородной среде (напр., ионосферный В., подводные звуковые каналы). Особенность В.— существо­вание в них дискретного (при не очень сильном поглощении) набора нормаль­ных волн (мод), распространяющихся со своими фазовыми и групповыми скоростями. Каждая мода характери­зуется предельной частотой, наз. кри­тической. Мода может распростра­няться и переносить вдоль В. поток энергии только при частотах, превы­шающих критич. частоту (см. Радио­волноводы). В нек-рых практически важных случаях (многопроводные ли­нии передачи, полые акустич. В.) возможно существование мод, не имеющих критич. частот.

• См. лит. при ст. Радиоволноводы, Нор­мальные волны.

М. А. Миллер.

ВОЛНОВОД АКУСТИЧЕСКИЙ, уча­сток среды, ограниченный в одном или двух направлениях стенками или др. средами, в результате чего устра­няется или уменьшается расхождение волн в стороны, так что распростра­нение звука вдоль участка происхо­дит с ослаблением меньшим, чем в неограниченной однородной среде. Искусственные В. а.— обычно трубы, ограниченные звуконепроницаемыми стенками (напр., вентиляц. каналы, туннели). Естественные В. а.— обыч­но слои среды. Напр., для низких частот звука океан представляет собой волновод в виде слоя воды, ограничен­ного с одной стороны грунтом, а с другой — свободной поверхностью воды. В. а. может быть образован слоистой неоднородностью среды в вертик. направлении (напр., подвод­ный звук. канал в океане): волны, пересекающие слой, в к-ром скорость звука имеет мин. значение, под ма­лыми углами, заворачивают к нему обратно в результате рефракции в смежных слоях с большей скоростью звука, как бы отражаясь от этих слоев (см. Гидроакустика). В отличие от труб, в к-рых звук может распрост­раняться только вдоль одной прямой (оси трубы), звук в слое может также распространяться в виде цилиндри­чески расходящейся волны.

Любое звук. поле внутри В. а. может быть представлено в виде супер­позиции нормальных волн. В простей­шем случае двухмерного распростра­нения звука в однородном слое или в трубе прямоуг. сечения норм. волна представляет собой гармоническую волну, бегущую вдоль В. а. и стоя­чую в поперечном направлении. При данной частоте в В. а. (как и в радио­волноводе) может существовать беско­нечный дискр. набор норм. волн, различающихся фазовой скоростью и числом узловых линий звук. поля в поперечном направлении: каждой норм. волне приписывают номер, рав­ный числу этих узлов. Для каждой норм. волны i имеется своя частота, наз. критической _кр, к-рая растёт с увеличением номера волны. Ниже этой частоты норм. волна не распрост­раняется, а превращается в синфаз­ное колебание с амплитудой, меняю­щейся вдоль волновода по экспонен­циальному закону. Исключение пред­ставляют В. а. с абсолютно жёсткими или упругими стенками: в них нуле­вая норм. волна, критич. частота к-рой _кр=0. может бежать при любой частоте.

При трёхмерном распространении звука в трубе также может существо­вать бесконечный дискр. набор норм. волн. Они отличаются от норм. волн при двухмерном распространении тем, что у них стоячая волна в поперечном сечении имеет не одно, а два семейства узловых линий. В трубе прямоуг. сечения узловые линии параллельны одной и другой паре противополож-

83


ных стенок: в круглой трубе узловые линии — концентрич. окружности и диаметры. Каждая норм. волна при трёхмерном распространении получает двойной номер, указывающий числа узловых линий одного и другого се­мейства. Эти норм. волны также имеют свои критич. частоты, ниже к-рых, как и в двухмерном случае, распространение прекращается.

В В. а. любую гармонич. волну можно представить в виде суперпози­ции норм. волн разных номеров той же частоты. При заданной частоте рас­пространяется только конечное число норм. волн низших номеров. Поэтому структура распределения звук. поля поперёк волновода, соответствующая высоким номерам норм. волн, вдоль волновода не передаётся. Норм. волны характеризуются значит. дисперсией скорости. В В. а. фазовая скорость норм. волн нулевого номера всегда больше, а групповая скорость — мень­ше, чем скорость звука с в неогранич. среде; с увеличением частоты первая убывает, а вторая растёт, и обе стре­мятся асимптотически к с. Исключе­ние составляет нулевая норм. волна в В. а. с абсолютно жёсткими стен­ками; в этом случае — это обычная бездисперсная плоская волна, бегу­щая без изменений при любой форме профиля, как в неогранич. среде.

В искусств. В. а. со слоисто не­однородной средой и в естеств. В. а. также могут существовать бесконеч­ные дискр. наборы норм. волн с ана­логичными св-вами. Напр., при сло­истой неоднородности среды, запол­няющей волновод, стоячая волна в поперечном направлении уже не будет синусоидальной, но норм. волны по-прежнему можно нумеровать по числу узловых линий в поперечном сечении. Дисперс. св-ва естеств. В. а. обычно существенно отличаются от дисперс. св-в однородных волноводов.

Твёрдые В. а. обычно ограничены свободными границами (стержни, пластины). Норм. волны в твёрдых В. а. образованы либо только сдвиговыми волнами горизонт. поляризации, либо совместно распространяющимися про­дольными и сдвиговыми волнами вертик. поляризации, преобразующимися друг в друга при отражениях на гра­ницах. В УЗ технологии твёрдым В. а. наз. также всякое устройство (стержни, концентраторы) для пере­дачи колебат. энергии на нек-рое рас­стояние от источника или для введе­ния колебат. энергии в к.-л. среду.

• Р ж е в к и н С. Н., Курс лекций по теории звука, М., 1960, гл. 6; Исакович М. А., Общая акустика, М., 1973.

М. А. Исакович.

ВОЛНОВОД ОПТИЧЕСКИЙ, то же, что световод.

ВОЛНОВОДНАЯ АНТЕННА, отрезок радиоволноеода с излучающим откры­тым концом. В. а. имеет широкую диаграмму направленности, широкополосна. В. а.— основные элементы антенных решёток сантиметрового диапазона.

• См. лит. при ст. Антенна.

ВОЛНОВОЕ СОПРОТИВЛЕНИЕ в аку­стике, в газообразной или жидкой среде — отношение звукового давления р в бегущей плоской волне к коле­бательной скорости v ч-ц среды. В. с. не зависит от формы волны и выражается ф-лой: p/v=c, где  — плотность среды, с — скорость звука. В. с. представляет собой уд. импеданс среды для плоских волн (см. Импе­данс акустический).

В. с.— важнейшая хар-ка среды, определяющая условия отражения и преломления волн на её границе. При норм. падении плоской волны на плоскую границу раздела двух сред коэфф. отражения определяется только отношением В. с. этих сред; если В. с. сред равны, то волна проходит границу без отражения. Понятием b.с. можно пользоваться и для тв. тела (для продольных и поперечных упругих волн в неограниченном тв. теле и для продольных волн в стерж­не), определяя В. с., как отношение соответствующего механич. напряже­ния, взятого с обратным знаком, к колебат. скорости ч-ц среды.

К. А. Наугольных.

ВОЛНОВОЕ СОПРОТИВЛЕНИЕ в гид­роаэромеханике. 1) b.c. в газо­вой динамике — аэродинамиче­ское сопротивление, возникающее, ког­да скорость газа относительно тела превышает скорость распространения в газе слабых (звуковых) возмущений (т. е. при сверхзвуковом течении). В. с.— результат затрат энергии на образование ударных волн. Оно в не­сколько раз превышает сопротивле­ние, связанное с трением и образова­нием вихрей, и зависит от формы тела, угла атаки и Маха числа M=v!c. Коэфф. В. с. резко увеличивается при приближении скорости тела v к ско­рости звука с в среде, иначе говоря, при приближении числа М к единице он проходит через максимум при не­больших сверхзвук. скоростях (волн. кризис), а затем постепенно умень­шается (см. Аэродинамические коэф­фициенты).

2) В. с. в тяжёлой жидкос­ти — одна из составляющих сил со­противления жидкости движению тел. В. с. возникает при движении тела вблизи свободной поверхности жид­кости или поверхностей раздела жид­костей с разл. плотностью. Оно обус­ловлено образованием волн на по­верхности жидкости, создаваемых дви­жущимся телом, к-рое при этом со­вершает работу по преодолению реак­ции жидкости: эта реакция и пред­ставляет собой силу В. с. Величина В. с. зависит от формы тела, глубины его погружения под свободную по­верхность, скорости движения, а так­же от глубины и ширины фарватера, где происходит движение. Волнообразование при движении тела зависит

от Фруда числа Fr= v²/gl (v—скорость поступат. движения тела, l — его длина, g — ускорение силы тяжести), к-рое явл. критерием подобия при моделировании движений, и В. с. гео­метрически подобных тел. Если для тела (судна) и его модели числа ft равны, то получается геом. подобие картин волнообразования, а также и равенство безразмерных коэфф. их

В. с. с_в=R_в/(v²S/2), где R_в — сила

В. с.,  — плотность жидкости, S— площадь смоченной поверхности тела. Для определения В. с. в обоих случаях пользуются как теоретиче­скими, так и эксперим. методами.

ВОЛНОВОЕ СОПРОТИВЛЕНИЕ ли­ний передачи, отношение напряжения к току в любой точке линии, по к-рой распространяются волны. В. с. играет роль сопротивления, к-рое оказывает линия бегущей волне напряжения и тока. При отсутствии потерь, когда линия может передавать в нагрузку практически всю энергию от генера­тора (см. Линии передачи), В. с. Z_B двухпроводной линии равно: Z_B= LIC Ом, где L и С — индуктив­ность и ёмкость ед. длины линии. Применяемые на практике линии пере­дачи (двухпроводные, коаксиальные) имеют В. с. ~10—10² Ом. Нагрузку линии подбирают равной В.с. (или близкой к нему), что обеспечивает наибольший коэфф. бегущей волны, с увеличением к-рого растёт кпд ли­нии.

Иногда понятие b.с. переносят на произвольное распределение электрич, и магн. полей в свободном пр-ве, в частности на отношение их ампли­туд в распространяющихся эл.-магн. волнах. Однако обычно для этого пользуются термином импеданс харак­теристический.

ВОЛНОВОЕ УРАВНЕНИЕ в механике, линейное однородное дифф. ур-ние в частных производных, описывающее распространение волн в среде; имеет вид:



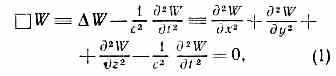
где t — время, х, у, z — пространст­венные декартовы координаты, W= W(х, у, z, t) — ф-ция, характери­зующая возмущение среды в точке с координатами х, у, z в момент вре­мени t, с — параметр с размерностью скорости, [ — оператор Д'Аламбера (даламбертиан),  — оператор Лап­ласа (лапласиан).

Частными видами В. у. (1) явл. двухмерное и одномерное В. у.; по­следнее совпадает с ур-нием колеба­ний идеально упругой струны:



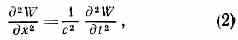
решение к-рого может быть представ­лено в виде двух волн, перемещаю­щихся в пр-ве со скоростью с:

84


W=f₁(x+ct)+ f₂(x-ct). (3)

Каждая из этих волн и составляет моду, распространяющуюся только в одном направлении (±х) и удовлетво­ряющую В. у. 1-го порядка (ур-нию волны):



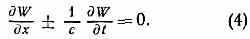
В. у. (1) допускает разделение пере­менных по координатам и времени: W=W₁(x,y,z)(t). При гармонич. зависимости от времени, выражен­ной с помощью комплексной записи =е^it, где (=kc, k — волн. число (см. Комплексная амплитуда). В. у. превращается в ур-ние Гельмгольца:

W+k²W =0, (5)

к-рое в двухмерном случае даёт ур-ние мембраны, а в одномерном — ур-ние осциллятора.

В. у. наз. неоднородным, если в его правой части стоит заданная ф-ция координат и времени, т. е.

W=f(x, y, z, t). (6)

В отличие от однородного В. у. не­однородное В. у., помимо собств. ре­шений — нормальных волн, сущест­вующих независимо от источника, имеет и вынужденное решение, описы­вающее движения (колебания, волны и др.), возбуждённые источниками.

В. у. описывает почти все разно­видности малых колебаний в распре­делённых механич. системах (продоль­ные звук. колебания в газе, жидкости, тв. теле, поперечные колебания в стру­нах, на поверхности воды и др.). В. у. удовлетворяют компоненты век­торов эл.-магн. поля и потенциалов, и поэтому многие явления эл.-магн. поля (от квазистатических до опти­ки) описываются с его помощью.

Среди нелинейных обобщений В. у. наиболее известны нелинейное ур-ние Клейна — Гордона:

W = m²W+F(W) (7)

(т — масса ч-цы), к-рое при F 0 вы­рождается в Клейна — Гордона — Фока уравнение, и нелинейное ур-ние Гельм­гольца:

W + k²W=F(│W│²)W. (8)

Нелинейные В. у. позволяют описать такие явления, как вз-ствие монохроматич. волн, возникновение и эво­люцию ударных волн и солитонов, самофокусировку. В квантовой ме­ханике В. у. иногда наз. Шрёдингера уравнение.

• Уизем Дж., Линейные и нелинейные волны, пер. с англ., М., 1977.

М. А. Миллер, Е. И. Якубович.

ВОЛНОВОЕ ЧИСЛО, модуль волно­вого вектора; связан с круговой час­тотой (о, фазовой скоростью волны v_ф и её пространств. периодом (дли­ной волны ) соотношением: k=2/=/v_ф. В оптике и спектроскопии В. ч. часто наз. величину, обратную длине волны: k=1/.

ВОЛНОВОЙ ВЕКТОР, вектор k, на­правление к-рого совпадает с направ­лением распространения бегущей вол­ны. Модуль В. в. наз. волн. числом. Групповая скорость и поток энергии волны направлены вдоль k, вообще говоря, только в изотропных средах. В случае квазиплоских и квазимоно-хроматич. волн В. в., определяемый как градиент фазы, явл. медленно меняющейся ф-цией координат и вре­мени.

В квант. механике состояние сво­бодной ч-цы характеризуется определ. значением В. в. k, связанного с им­пульсом р частицы соотношением де Бройля:

p=hk

(см. Корпускулярно-волновой дуализм).

М. А. Миллер.

ВОЛНОВОЙ ПАКЕТ, распространя­ющееся волн. поле, занимающее в каждый момент времени огранич. об­ласть пр-ва. Возникновение В. п. воз­можно у волн любой природы (зву­ковых, эл.-магн. и т. п.). Такой волн. «всплеск» в нек-рой области пр-ва может быть разложен на сумму пло­ских монохроматич. волн (распрост­раняющихся в близких направлениях), частоты к-рых лежат в определ. пре­делах. Однако чаще термином «В. п.» пользуются в квант. механике.

В квант. механике каждому состоя­нию ч-цы с определ. значениями им­пульса и энергии соответствует пло­ская монохроматич. волна де Бройля, занимающая всё пр-во. Координата ч-цы с точно определённым импуль­сом полностью неопределённа — ч-ца с равной вероятностью может быть обнаружена в любом месте пр-ва, по­скольку эта вероятность пропорц. квадрату амплитуды волны де Брой­ля. Это отвечает неопределённостей соотношению, утверждающему, что чем определённее импульс ч-цы, тем менее определённа её координата. Если же ч-ца локализована в нек-рой огранич. области пр-ва, то её импульс уже не явл. точно определённой вели­чиной — имеется нек-рый разброс воз­можных его значений.




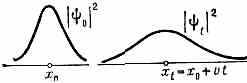
Расплывание волн. пакета о течением вре­мени t. В нач. момент времени ч-ца описы­вается волн. пакетом ₀, в момент t — волн. пакетом _t; |₀|² и |_t|² определяют вероят­ности нахождения ч-цы в нек-рой точке х; v — скорость центра пакета, совпадающая с мехаиич. скоростью ч-цы. Площади, ограничен­ные кривыми и осью абсцисс, одинаковы и дают полную вероятность нахождения ч-цы в пр-ве в данный момент времени.


Состояние та­кой ч-цы представится суммой (точ­нее, интегралом, т. к. импульс свобод­ной ч-цы изменяется непрерывно) монохроматич. волн с частотами, со­ответствующими интервалу возмож­ных значений импульса. Наложение (суперпозиция) группы таких волн,

имеющих почти одинаковое направле­ние распространения, но слегка отли­чающихся по частотам, и образует В. п. В квант. механике это означает, что вероятность нахождения ч-цы в области, занимаемой В. п., велика, а вне этой области практически равна нулю. Оказывается, что скорость В. п. свободной ч-цы (точнее, его центра) совпадает с механической скоростью ч-цы.

В. п. описывает движущуюся ч-цу, локализованную в каждый данный момент времени в нек-рой огранич. области координат, то есть В. п. явл. волновой функцией такой ч-цы.

С течением времени В. п. свободной ч-цы становится шире, «расплывается» (рис.) вследствие того, что составляю­щие пакет монохроматич. волны с раз­ными частотами распространяются даже в пустоте с разл. скоростями. «Расплывание» В. п. соответствует уве­личению области возможной локали­зации ч-цы.

Если ч-ца не свободна, а находится вблизи нек-рого центра притяжения (напр., эл-н в кулоновском поле про­тона в атоме водорода), то такой связ. ч-це будут соответствовать стоячие волны, сохраняющие стабильность. Форма В. п. при этом остаётся неиз­менной, что отвечает стационарному

состояния системы.

В. И. Григорьев.