Вавилова закон
| Вид материала | Закон |
- Н. И. Вавилова аналитический отчет, 217.51kb.
- Урок по общей биологии в 11 классе «Дело академика Вавилова», 851.64kb.
- Селекция- одомашнивание, 126.51kb.
- Уважаемые коллеги!, 64.43kb.
- Українське товариство генетиків І селекціонерів ім. М.І. Вавилова, 45.97kb.
- «Саратовский государственный аграрный университет имени Н. И. Вавилова», 377.27kb.
- Саратовский Государственный Аграрный Университет им. Н. И. Вавилова. Кафедра Акушерства, 248.61kb.
- О. Б. Ширяев Институт общей физики ран, 119991, Москва, ул. Вавилова,, 20.28kb.
- Главное управление образования, 70.84kb.
- Издательский дом, 529.99kb.
ВОЛНЫ, изменения состояния среды (возмущения), распространяющиеся в этой среде и несущие с собой энергию. Наиболее важные и часто встречающиеся виды В.— упругие волны, волны на поверхности жидкости и электромагнитные волны. Частными случаями упругих В. являются звук. и сейсмич. волны, а электромагнитных — радиоволны, свет, рентг. лучи и др. Осн. св-во всех В., независимо от их природы, состоит в том, что в В. осуществляется перенос энергии без переноса в-ва (последний может иметь место лишь как побочное явление). Волн. процессы встречаются почти во всех областях физ. явлений, поэтому их изучение имеет большое значение.
В. могут различаться по тому, как возмущения ориентированы относительно направления их распространения. Так, напр., звуковая В. распространяется в газе в том же направлении, в каком происходит смещение ч-ц газа (рис. 1, а); при распространении В. вдоль струны смещение точек струны происходит в направлении, перпендикулярном струне
85
(рис. 1, б). В. первого типа наз. продольными, а второго — поперечными. В жидкостях и газах упругие силы возникают только при сжатии и не возникают при сдвиге, поэтому упругие деформации в жидкостях и газах
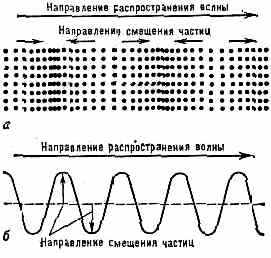
Рис. 1.a — продольная волна; б — поперечная волна.
могут распространяться только в виде продольных В. («волны сжатия»). В тв. телах, в к-рых упругие силы возникают также при сдвиге, упругие деформации могут распространяться не только в виде продольных В., но и в виде поперечных («волны сдвига»). В тв. телах огранич. размера (напр., в стержнях, пластинках) картина распространения В. более сложна: здесь возникают ещё и др. типы В., являющиеся комбинацией первых двух осн. типов.
В эл.-магн. В. направления электрич. и магн. полей почти всегда (за исключением случаев анизотропных сред и распространения в несвободном пр-ве) перпендикулярны направлению распространения В., поэтому эл.-магн. В. в свободном пр-ве поперечны.
Общие характеристики и свойства волн. В. могут иметь разл. форму. Одиночной В., или импульсом, наз. сравнительно короткое возмущение, не имеющее регулярного хар-ра (рис. 2, а). Ограниченный ряд повторяющихся возмущений наз, ц у г о м В. Обычно понятие цуга относят к отрезку синусоиды (рис. 2, б). Особое значение в теории В. имеет
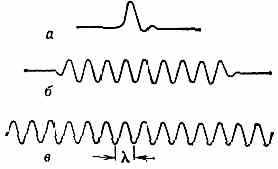
Рис. 2. а — одиночная волна; б — цуг волн; в — бесконечная синусоидальная волна.
представление о гармонич. В., т. е. бесконечной синусоидальной В., в к-рой все изменения состояния среды происходят по закону синуса или косинуса (рис. 2, в), поскольку такие В. могли бы распространяться в однородной среде (если амплитуда их невелика) без искажения формы (о В. большой амплитуды см. ниже). Основными хар-ками гармонич. В. являются длина В. — расстояние между двумя максимумами или минимумами возмущения и период В. Т — время, за к-рое совершается один полный цикл колебания. Длина В. связана с периодом Т соотношением с=Т, где с — скорость распространения В. Это соотношение справедливо для гармонич. В. любой природы. Вместо периода Т нередко пользуются частотой f, равной числу периодов в ед. времени: f=1/T, при этом f=с. В теории В. пользуются также понятием волнового векторa k, по абс. величине k=2= 2f/с, т. е. равен числу длин В. на отрезке 2я и ориентирован в направлении распространения В.
В гармонич. В. изменение колеблющейся величины W во времени описывается в каждой точке ф-лой: W=Asin2t/T (где t — время), т. е. эта величина совершает гармонические колебания. В положении равновесия величина W принимается равной нулю. А — амплитуда В., т. е. значение, к-рое эта величина принимает при наибольших отклонениях. В любой другой точке, расположенной на расстоянии r от первой в направлении распространения В., изменение W со временем происходит по такому же закону, но с опозданием на время . t1=r/c, что можно записать в виде:
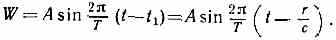
Выражение =(2/T)(t-t1) наз. фазой
В. Разность фаз в двух точках r1, и r2 равна:
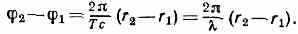
В точках, отстоящих друг от друга на целое число , разность фаз составляет чётное число л, т. е. колебания в этих точках протекают в одинаковой фазе — синфазно. Наоборот, в точках, отстоящих друг от друга на нечётное число полуволн, т. е для к-рых r2-r1=(2N-1)/2, где N= 1, 2, . . ., разность фаз равна нечётному числу л, т. е. 2-1=(2N-1). Колебания в таких точках происходят в противофазе: в то время как отклонение в одной равно А, в другой оно равно — А, а наоборот. Распространение В. всегда связано с переносом энергии, к-рый можно количественно характеризовать вектором плотности потока энергии I. Этот вектор для упругих В. наз. вектором Умова (по имени рус. учёного Н. А. Умова, к-рый ввёл это понятие), для электромагнитных — Пойнтинга вектором. Направление вектора I совпадает с направлением переноса энергии, а его абс. величина равна энергии, переносимой В. за ед. времени
через единичную площадку, расположенную перпендикулярно к нему. При малых отклонениях от положения равновесия I=КА2, где К — коэфф. пропорциональности, зависящий от природы В. и св-в среды, в к-рой В. распространяется.
Важной хар-кой В. явл. вид поверхностей равных фаз, т. е. таких поверхностей, в любой точке к-рых в данный момент времени фазы одинаковы. Форма поверхности равной фазы зависит от условий возникновения и распространения В. В простейшем случае такими поверхностями явл. плоскости, перпендикулярные направлению распространения В.; такая В. наз. п л о с к о й. В., у к-рых поверхностями равных фаз явл. сферы и цилиндры, наз. соответственно сферическими и цилиндрическими. Поверхности равных фаз наз. также фронтами В. В случае одиночной В. фронтом наз. передний край В., непосредственно граничащий с невозмущённой средой.
Волны и лучи. Линия, направление к-рой в каждой точке совпадает с направлением потока энергии в В., наз. лучом. В изотропной среде это направление совпадает с направлением нормали к фронту В. Плоской В. соответствует параллельный пучок прямолинейных лучей, сферической — радиально расходящийся пучок и т. д, При нек-рых условиях сложный расчёт распространения В. можно заменить более простым расчётом формы лучей. Этим пользуются в геометрической акустике и геометрической оптике. Такой упрощённый подход применим, когда длина В. достаточно мала по сравнению с нек-рыми характерными размерами, напр. размерами препятствий, лежащих на пути

Рис. 3. Интерференция волн на поверхности воды, возбуждаемых в двух разл. точках.
распространения В., поперечными размерами фронта В., расстояниями до точки, в к-рой сходятся В., и т. п. Интерференция волн. При приходе в данную точку среды двух В. их действие складывается. Особо важное значение имеет наложение т. н.
86
когерентных В. В случае когерентности В. имеет место явление, наз. интерференцией: в точках, куда обе В. приходят в фазе, они усиливают друг друга; в точках же, куда они попадают в противофазе, ослабляют.
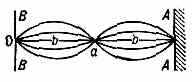
Рис. 4. Стоячая волна, возникшая в результате интерференции падающей и отражённой от препятствия А А волны: в точке а — узел колебания, в точках b — пучности.
В результате получается характерная интерференц. картина (рис. 3). См. также Интерференция волн, Интерференция света.
Один из важных и часто встречающихся случаев — интерференция прямой и обратной В. (рис. 4), распространяющихся в противоположных направлениях, к-рая приводит к образованию т. н. стоячих волн.
Дифракция. При падении В. на непрозрачное для неё тело или на экран позади тела образуется теневое пр-во (рис. 5, а и 6, слева).
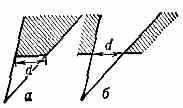
Рис.5. Схема образования тени при падении волны: а — на непрозрачное тело; б — на отверстие в непрозрачном экране (d — размер тела или отверстия).
Однако границы тени не резки, а размыты, причём размытость увеличивается при удалении от тела. Это явление огибания тела В. наз. дифракцией. На расстояниях от тела, существенно больших, чем d2/, где d — его поперечный размер, тень практически полностью смазана.
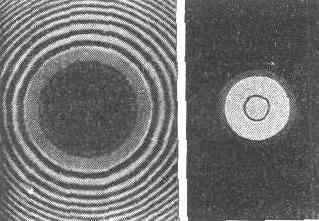
Рис. 6. Дифракц. картина при падении света: слева — на круглый экран; справа — на круглое отверстие.
Чем больше размеры тела, тем большее пр-во занимает тень. Тела, размеры к-рых малы по сравнению с длиной В., вообще не создают тени, они рассеивают падающую на них В. во всех направлениях. Изменение амплитуды В. при переходе из «освещённой» области в область тени происходит по сложному закону с чередующимися уменьшением и увеличением амплитуды (рис.
6, слева и 7), что обусловлено интерференцией В., огибающих тело.
Дифракция имеет место также при прохождении В. через отверстие (рис. 5, б и 6, справа), где она также выражается в проникновении В. в область тени и в нек-ром изменении хар-ра В. в освещённой области: чем меньше диаметр отверстия по сравнению с длиной В., тем шире область, в к-рую проникает В.
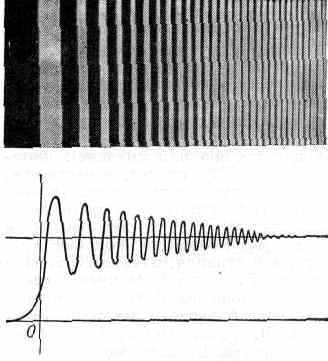
Рис. 7. Вверху — дифракция света от края экрана (виден сложный переход от света к тени); внизу — кривая, характеризующая освещённость пр-ва между светом и тенью (край экрана соответствует началу координат).
См. Дифракция волн, Дифракция света.
Поляризация волн заключается в нарушении симметрии распределения возмущений (напр., смещений и скоростей в упругих В. или напряжённостей электрич. и магн. полей в эл.- магн. В.) относительно направления распространения поперечной В. В продольной В., в к-рой возмущения всегда направлены вдоль направления распространения В., явления поляризации возникнуть не могут.

Рис. 8. а — линейно поляризованная волна; б — волна, поляризованная по кругу (E — вектор, изображающий распространяющееся возмущение).
Если колебания возмущения E происходят всё время в каком-то одном направлении (рис. 8, а), то имеет место простейший случай линейно поляризованной или плоско поляризованной В. Возможны и другие, более сложные типы поляризации. Напр., если конец вектора E, изображающего возмущение, описывает эллипс или окружность в плоскости колебаний (рис. 8, б), то имеет место эллиптическая или круговая поляризация. Скорость распространения поперечных В. может зависеть от их поляризации. Поляризация может возникнуть: из-за отсутствия симметрии в возбуждающем В. излучателе, при распространении В. в анизотропной среде, при преломлении и отражении В. на границе двух сред. См. также Поляризация света.
Отражение и преломление волн. При падении на плоскую границу раздела двух разных сред плоская В. частично отражается, частично проходит в другую среду, оставаясь плоской,
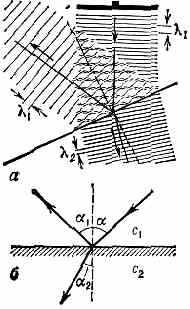
Рис. 9. а — схема отражения и преломления плоской волны (1 — длина падающей и отражённой волн, г — длина преломлённой волны); б— схема хода лучей (стрелки), соответствующих падающей, отражённой и преломлённой волнам.
но меняет при этом своё направление распространения (преломляется) (рис. 9, а). Углы, образуемые направлениями падающей и преломлённой В. (рис. 9, б) с перпендикуляром к границе раздела сред, наз. соотв. углом падения , углом отражения 1 и углом преломления 2. Согласно закону отражения, угол падения равен углу отражения, т. е. =1, a согласно закону преломления, синус угла падения относится к синусу угла преломления, как скорость В. в первой среде к её скорости во второй среде, т. е. sin/sin2=с1/с2=n, где n — показатель преломления.
Смесь В. с разл. поляризациями, распространяющихся в одном и том же направлении, разделится, попадая в среду, в к-рой скорость распространения зависит от состояния поляризации: В., поляризованные различно, пойдут по разным направлениям (см. Двойное лучепреломление). Во многих случаях скорость распространения зависит также от частоты колебаний
87
(т. е. имеет место дисперсия); в этих случаях смесь В. с разл. частотами при преломлении разделится. При отражении расходящейся (сферич. или цилиндрической) В. под малыми углами к плоской границе раздела двух сред возникают нек-рые особенности. Так, напр., когда скорость с2 в ниж. среде больше, чем с1 в верх. среде, кроме обычной отражённой В., к-рой соответствует луч ОАР, возникает т. н. боковая В. Соответствующий ей луч OSDP часть своего пути (отрезок SD) проходит в среде, от к-рой
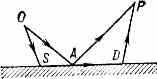
Рис. 10. Схема образования боковой волны.
происходит отражение (рис. 10). Иногда, особенно в сейсмологии, боковая В. наз. головной.
Форма волны. В процессе распространения В. её форма претерпевает изменения. Хар-р изменений существенно зависит от первонач. формы В. Лишь бесконечная синусоидальная (гармоническая) В. (за исключением В. очень большой интенсивности) сохраняет свою форму неизменной при распространении, если при этом она не испытывает заметного поглощения. Но всякую В. (любой формы) можно представить как сумму бесконечных гармонич. В. разных частот (гармоник). Напр., одиночный импульс можно представить как бесконечную сумму наложенных друг на друга гармонич. В. Если среда, в к-рой распространяются В., линейна, т. е. её св-ва не меняются под действием возмущений, создаваемых В., то все эффекты, вызываемые негармонич. В., могут быть определены как сумма эффектов, создаваемых в отдельности каждой из её гармонич. составляющих (т. н. суперпозиции принцип).
В реальных средах нередко скорости распространения гармонич. В. зависят от частоты В. (т. н. дисперсия В.). Поэтому негармонич. В., состоящая из совокупности гармоник, в процессе распространения меняет свою форму, т. к. соотношение между фазами составляющих её гармонич. В. меняется. Искажение формы В. может происходить и при дифракции и рассеянии негармонич. В., т. к. оба эти процесса зависят от длины В., и поэтому для гармонич. В. разной длины дифракция и рассеяние будут различны. При наличии дисперсии форма негармонических В. может изменяться также в результате её преломления. Иногда может искажаться и форма гармонических В. Это происходит в тех случаях, когда амплитуда распространяющейся В. достаточно велика, так что уже нельзя пренебрегать изменениями св-в среды под её воздействием, т. е. когда сказываются нелинейные св-ва среды. В нелинейной среде существенно изменяются и др. законы распространения В., в частности возникает новый тип уединённых волн — соли-тоны, изменяются законы отражения и преломления (см. Нелинейная оптика).
Фазовая и групповая скорости. Введённая выше скорость В. наз. фазовой скоростью, это скорость, с к-рой перемещается к.-н. определ. фаза бесконечной синусоидальной (монохроматической) В. (напр., фаза, соответствующая гребню или впадине). Фазовая скорость В. входит, в частности, в ф-лу закона преломления. Однако на практике имеют дело не с монохроматич. В., для к-рых только и имеет смысл понятие фазовой скорости, а с огранич. цугами В. Любая огранич. В. может быть представлена в виде наложения большого (точнее, бесконечно большого) числа монохроматич. В. разл. частот. Если фазовые скорости В. всех частот одинаковы, то с этой же скоростью распространяется и вся совокупность, или группа, В. Если же эти скорости неодинаковы, то имеет место дисперсия, и вопрос о скорости распространения В. усложняется. Если ограниченная В. состоит из В., частоты к-рых мало отличаются друг от друга, то эта В. (т. н. волновой пакет) распространяется с определ. скоростью, наз. групповой скоростью: и=с-dc/d,. С групповой же скоростью происходит перенос энергии В.
Эффект Доплера. При движении источника или наблюдателя происходит изменение частоты В. Наблюдатель, движущийся по направлению к источнику В. (любого вида), воспринимает несколько повышенную частоту по сравнению с неподвижным наблюдателем, между тем как наблюдатель, удаляющийся от источника В., воспринимает пониженную частоту. Аналогичное явление (качественно) имеет место также, когда наблюдатель неподвижен, а источник В. движется. См. также Доплера эффект.
Излучение и распространение волн. Для излучения В. необходимо произвести в среде нек-рое возмущение за счёт внеш. источника энергии. Работа, совершаемая этим источником, за вычетом нек-рых потерь превращается в энергию излучаемых В. Так, напр., мембрана телефона или диафрагма громкоговорителя, получая энергию от электроакустического преобразователя, излучает звуковые В. Излучение В. производится всегда источниками огранич. размеров, в результате чего возникает «расходящаяся» В.
Несмотря на разную природу В., закономерности, к-рыми определяется их распространение, имеют между собой много общего. Так, упругие В. в однородных жидкостях (газах)
или эл.-магн. В. в свободном пр-ве, возникающие в к.-л. малой области («точке») и распространяющиеся без поглощения в окружающем пр-ве, описываются одним и тем же волновым уравнением.
• Горелик Г. С., Колебания и волны, 2 изд., М., 1959; Бреховских Л. М., Волны в слоистых средах, 2 изд., М., 1973; Крауфорд Ф., Волны, пер. с англ., М., 1974 (Берклеевский курс физики, т. 3); Пирс Дж., Почти все о волнах, пер. с англ., М., 1976; Уизем Дж., Линейные и нелинейные волны, пер. с англ., М., 1977; Виноградова М. Б., Руденко О. В., Сухоруков А. П., Теория волн, М., 1979.
Л. М. Бреховских.
ВОЛНЫ ДЕ БРОЙЛЯ, волны, связанные с любой микрочастицей и отражающие их квант. природу.
В 1924 франц. физик Л. де Бройль (L. de Broglie) высказал гипотезу о том, что установленный ранее для фотонов корпускулярно-волновой дуализм (заключающийся в том, что фотоны обладают и св-вами ч-ц, корпускул, и волн. св-вами) присущ всем ч-цам — эл-нам, протонам, атомам и т. д., причём количеств. соотношения между воли. и корпускулярными св-вами ч-ц те же, что для фотонов. Т. о., если ч-ца имеет энергию ξ и импульс, абс. значение к-рого равно р, то с ней связана волна, частота к-рой v=ξ/h и длина =h/p. Эти волны и получили назв. В. де Б.
Для ч-ц не очень высокой энергии (v<
Первое эксперим. подтверждение гипотезы де Бройля было получено в 1927 в опытах амер. физиков К. Дэвиссона п Л. Джермера. Пучок эл-нов ускорялся в электрич. поле с разностью потенциалов 100—150 В (энергия таких эл-нов 100—150 эВ, что соответствует 1 Å) и падал на кристалл никеля, играющий роль пространств. дифракц. решётки. Было установлено, что эл-ны дифрагируют на кристалле, причём именно так, как должно быть для волн, длина к-рых определяется соотношением де Бройля. Волн. св-ва эл-нов, нейтронов и др. ч-ц, а также атомов и молекул теперь не только надёжно доказаны прямыми опытами, но и широко используются в установках с высокой разрешающей способностью, так что можно говорить об инженерном ис-
88
пользовании В. де Б. (см. Дифракция микрочастиц).
Подтверждённая на опыте идея де Бройля о двойств. природе микрочастиц — корпускулярно-волн. дуализме — принципиально изменила представления об облике микромира. Поскольку всем микрообъектам (по традиции за ними сохраняется термин «ч-цы») присущи и корпускулярные и волновые св-ва, то, очевидно, любую из этих «ч-ц» нельзя считать ни ч-цей, ни волной в классич. понимании. Возникла потребность в такой теории, в к-рой волн. и корпускулярные св-ва материи выступали бы не как исключающие, а как взаимно дополняющие друг друга. В основу такой теории — волновой, или квантовой, механики и легла концепция де Бройля. Ото отражается даже в назв. волновая функция для величины, описывающей в этой теории состояние системы. Квадрат модуля волн. ф-цин определяет вероятность состояния системы, и поэтому о В. де Б. часто говорят как о волнах вероятности (точнее, амплитуд вероятности). Для свободной ч-цы с точно заданным импульсом, движущейся вдоль оси х, волн. ф-ция имеет вид:
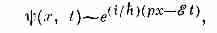
где h= h/2 (t — время). В этом случае ||2=const, т.е. вероятность обнаружить ч-цу во всех точках одинакова.
• См. лит. при ст. Квантовая механика.
В. И. Григорьев.
