Вавилова закон

Вид материала

Закон

Содержание Ван-дер-ваальсовы силы Вариационные принципы ме­ханики. N, направленной в любой момент времени по нормали Mn Вариньона многоугольник Q в электрич. цепях перем. тока: Q= UI Схема включения варметра W для измерения реактивной мощности в случае равномерно нагруженных фаз: 1 — последовательная цепь; 2 — В. П. Кузнецов. Ватт на квадратный метр Вейса индексы Векторное поле А. В. Ефремов. М. Ю. Хлопов. А. Д. Альтшуль. Фарадея эффект.

Подобный материал:

• Н. И. Вавилова аналитический отчет, 217.51kb.
• Урок по общей биологии в 11 классе «Дело академика Вавилова», 851.64kb.
• Селекция- одомашнивание, 126.51kb.
• Уважаемые коллеги!, 64.43kb.
• Українське товариство генетиків І селекціонерів ім. М.І. Вавилова, 45.97kb.
• «Саратовский государственный аграрный университет имени Н. И. Вавилова», 377.27kb.
• Саратовский Государственный Аграрный Университет им. Н. И. Вавилова. Кафедра Акушерства, 248.61kb.
• О. Б. Ширяев Институт общей физики ран, 119991, Москва, ул. Вавилова,, 20.28kb.
• Главное управление образования, 70.84kb.
• Издательский дом, 529.99kb.

ВАН-ДЕР-ВААЛЬСОВЫ СИЛЫ, рас­пространённое назв. сил межмолеку­лярного взаимодействия. ВАР (вольт-ампер реактивный, ВАр), единица СИ реактивной мощности переменного (синусоидального) электрич. тока. 1 ВАр равен реактивной мощности при действующих значениях электрич. напряжения 1 В, силы тока 1 А и при sin =1 ( — сдвиг фаз между напряжением и током в цепи).

ВАРИАНТНОСТЬ (от лат. varians — изменяющийся), число степеней сво­боды термодинамич. системы, т. е. число независимых физ. переменных (параметров системы), к-рые можно

изменять (варьировать) в определ. пределах, не нарушая фазового равно­весия в системе. См. Гиббса правило фаз.

ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕ­ХАНИКИ. Принципами механики наз. исходные положения, отражающие столь общие закономерности механич. явлений, что из этих положений как следствия можно получить ур-ния, определяющие движения механич. си­стемы (или условия её равновесия). В механике установлен ряд таких принципов, каждый из к-рых может быть положен в её основу и к-рые подразделяют на невариационные и вариационные.

Невариац. принципы механики не­посредственно устанавливают законо­мерности движения, совершаемого си­стемой под действием приложенных к ней сил. К ним относится, напр., 2-й закон Ньютона, Д'Аламбера прин­цип. Невариац. принципы справед­ливы для любой механич. системы и имеют сравнительно простое матем. выражение. Однако их применение ограничено только рамками механики, поскольку в выражения принципов непосредственно входит такое чисто механич. понятие, как сила. Сущест­венно также, что в большинстве задач механики рассматривается движение несвободных систем, т. е. систем, пере­мещения к-рых ограничены связями (см. Связи механические), напр. все­возможные машины, механизмы, на­земный транспорт, где связями явл. подшипники, шарниры, тросы, по­лотно дороги или рельсы и т. п. Ис­ходя из невариац. принципов при изучении движения несвободной си­стемы эффект действия связей учиты­вают введением нек-рых сил, наз. реакциями связей, величины к-рых заранее неизвестны, поскольку они за­висят от того, чему равны и где при­ложены действующие на систему за­данные (активные) силы, такие, напр., как сила тяжести, упругости пружин, тяги, а также от того, как при этом движется сама система. Поэтому в со­ставленные ур-ния движения войдут дополнит. неизвестные величины — реакции связей, что обычно сущест­венно усложняет решение этих ур-ний.

Преимущество В. п. м. состоит в том, что из них сразу получаются ур-ния движения соответствующей ме­ханич. системы, не содержащие неиз­вестных реакций связей. Достигается это тем, что эффект действия связей учитывается не заменой их неизвест­ными силами (реакциями), а рассмот­рением тех перемещений и движений (или приращений скоростей и ускоре­ний), к-рые точки этой системы могут иметь при наличии данных связей. Напр., если точка М движется по гладкой (идеальной) поверхности, яв­ляющейся для неё связью (рис. 1), то действие этой связи можно учесть,

67


заменив связь заранее неизвестной по величине реакцией N, направленной в любой момент времени по нормали Mn к поверхности (поскольку по этому направлению связь не даёт перемещаться точке). Но эффект этой же связи можно учесть, установив,



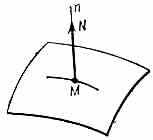
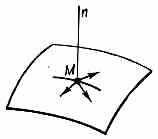
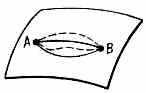
Рис. 1. Рис. 2. Рис. 3.


что для точки М в данном случае при любом её по­ложении возможны лишь элементы перемещения, пер­пендикулярные к

нормали Mn (рис. 2); такие пере­мещения наз. возможными переме­щениями. Наконец, эффект той же связи может быть охарактеризован и тем, что при этом движение точки из нек-рого положения А в положение В возможно только по любой кривой АВ, лежащей на поверхности, к-рая явл. связью (рис. 3); такие движения наз. кинематически воз­можными.

Содержание В. п. м. состоит в том, что они устанавливают св-ва (приз­наки), позволяющие отличить истин­ное, т. е. фактически происходящее под действием заданных сил, движе­ние механич. системы от тех или иных кинематически возможных её движе­ний (или же состояние равновесия системы от др. возможных её состоя­ний). Обычно эти св-ва (признаки) состоят в том, что для истинного движения нек-рая физ. величина, за­висящая от хар-к системы, имеет наи­меньшее значение по сравнению с её значениями во всех рассматриваемых кинематически возможных движе­ниях. При этом В. п. м. могут отли­чаться друг от друга видом указан­ной физ. величины и особенностями рассматриваемых кинематически воз­можных движений, а также особен­ностями самих механич. систем, для к-рых эти В. п. м. справедливы. Ис­пользование В. п. м. требует приме­нения методов вариац. исчисления.

По форме В. п. м. разделяют на т. н. дифференциальные, в к-рых устанавливается, чем истинное движение системы отличается от ки­нематически возможных движений в каждый данный момент времени, и интегральные, в к-рых это различие устанавливается для пере­мещений, совершаемых системой за к.-н. конечный промежуток времени. Дифференциальные В. п. м. в рамках механики явл. более общими и справедливы для любых механич. систем. Интегральные В. п. м. в их наиболее употребит. виде справедливы только для консервативных систем. Однако в них, в отличие от дифференциальных В. п. м. и невариац. принципов, вме­сто сил входит такая физ. величина, как энергия, что позволяет распрост­ранить эти В. п. м. и на немеханич. явления. К осн. дифференциальным В. п. м. относятся: возможных пере­мещений принцип, Д'Аламбера — Лагранжа принцип, Гаусса принцип (принцип наименьшего принуждения), а также тесно примыкающий к нему Герца принцип (принцип наименьшей кривизны). К интегральным В. п. м. относятся т. н. принципы наимень­шего (стационарного) действия, раз­ные формы к-рых отличаются друг от друга выбором величины действия и особенностями сравниваемых между собой кинематически возможных дви­жений системы (см. Наименьшего дей­ствия принцип). Применяются В. п. м. как для составления в наиболее про­стой форме ур-ний движения механич. систем, так и для изучения общих св-в этих движений. При соответст­вующем обобщении понятий они ис­пользуются также в механике сплош­ных сред, термодинамике, электроди­намике, квант. механике, теории от­носительности и др.

• Вариационные принципы механики. [Сб. статей], под ред. Л. С. Полака, М., 1959; Бухгольц Н. Н., Основной курс теоре­тической механики, 6 изд., ч. 2, М., 1972; Голдстейн Г., Классическая механика, пер. с англ., 2 изд., М., 1975; Кильчевский Н. А., Курс теоретической механики, 2 изд., т. 2, М., 1977. С. М. Тарг.

ВАРИНЬОНА МНОГОУГОЛЬНИК, то же, что многоугольник верёвочный.

ВАРИНЬОНА ТЕОРЕМА: если система сил F_i имеет равнодействующую В, то момент М₀ (R) равнодействующей относительно любого центра О (или оси z) равен сумме моментов M₀(F_i) составляющих сил относительно того же центра О (или той же оси г). Сфор­мулирована и доказана впервые франц. учёным П. Вариньоном (P. Varignon; 1687). Математически В. т. выра­жается равенствами:

M₀(R)=M₀(F_i)

или M_z(R)=М_z(F_i).

В. т. пользуются при решении ряда задач механики (особенно статики), сопротивления материалов, теории со­оружений и др.

ВАРМЕТР (от вар и греч. metreo — измеряю), прибор для измерения ре­активной мощности Q в электрич. цепях перем. тока: Q= UIsin, где U — напряжение, I — сила электрич. тока,  — фазовый угол между сину­соидально изменяющимися током и напряжением. Применяется в осн. в трёхфазных цепях перем. тока про­мышленной частоты (50 Гц). Схема включения В. такая же, как и ватт­метра. Основу В. составляет электроизмерит. механизм, обычно электродинамич. или ферродинамич. системы, и электрич. схема, обеспечивающая

пропорциональность показаний В. ве­личине sin. Для расширения пре­дела измерений В. применяют изме­рит. трансформаторы тока и напря­жения. В кач-ве В. могут быть ис­пользованы также ваттметры, вклю­чённые по спец. схеме (на рисунке — пример с равномерно нагруженными фазами).



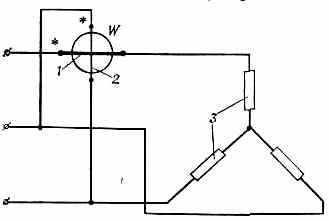
Схема включения варметра W для измерения реактивной мощности в случае равномерно нагруженных фаз: 1 — последовательная цепь; 2 — параллельная цепь; 3 — нагруз­ка.


Техн. требования к В. стандартизо­ваны в ГОСТах 22261 — 76 и 8476 — 60.

• Электрические измерения, под ред. Е. Г. Шрамкова, М., 1972; Справочник по электроизмерительным приборам, 2 изд., Л., 1977.

В. П. Кузнецов.

ВАТТ (Вт, W), единица СИ механич. мощности, а также активной мощ­ности электрич. цепи, мощности теп­лового потока или потока излучения, эквивалентных механич. мощности 1 Вт; названа в честь англ. изобрета­теля Дж. Уатта (J. Watt). 1 Вт равен мощности, при к-рой работа 1 Дж совершается за 1 с; 1 Вт=10⁷ эрг/с=0,102 кгс•м/с=1,36•10^-3 л. с.

ВАТТ НА КВАДРАТНЫЙ МЕТР (Вт/м², W/m²), единица СИ поверх­ностной плотности теплового потока; 1 Вт/м² равен поверхностной плот­ности теплового потока 1 Вт, равно­мерно распределённого по поверх­ности площадью 1 м². В ед. Вт/м² измеряют также поверхностную плот­ность потока излучения и соотв. энергетич. светимость и энергетич. освещённость.

ВАТТМЕТР (от ватт и греч. metreo — измеряю), прибор для измерения мощ­ности в электрич. цепях (в цепях перем. тока — для измерения активной мощности Р=UIcos, где U — напряжение, I — сила электрич. тока,  — фазовый угол между синусои­дально изменяющимися током и на­пряжением). Схема включения В. в цепь показана на рисунке.



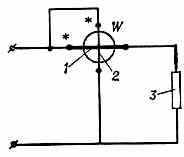
Схема включения ваттметра W: 1 — последовательная цепь (неподвижная катушка); 2 — па­раллельная цепь (подвижная катуш­ка); 3 — нагрузка. В электродинамич. ваттметре поворот под­вижной катушки в магн. поле неподвижной катушки пропорц. измеряемой мощности.


Для умень-

68


шения искажающего влияния после­довательная цепь В. должна обладать малым, а параллельная — большим сопротивлением. При измерениях на перем. токе важно также, чтобы со­противление параллельной цепи было чисто активным.

Осн. частью В. явл. электроизмерит. механизм обычно электродинамич. или ферродинамич. системы, реже — индукционной или электро­статической (см. соответств. статьи). Для расширения пределов измере­ний В. используют: на пост. токе — шунты и добавочные сопротивления, на перем. токе — измерит. трансфор­маторы тока и напряжения. Для из­мерения мощности на частотах выше 5 кГц, а также малой мощности (менее 100 мВт) применяют термоэлектрич. и терморезистивные В., В. на ПП элементах, В. с преобразователями Холла, пондеромоторные В., калориметрич. В. Ваттметры с электроизмерит. механизмом характеризуются след. данными: пределы по току — от 10 мА до 10 А, по напряжению — от 15 до 600 В, осн. погрешность в % от верх. предела измерений — до 0,2%. Применение измерит. трансфор­маторов тока и напряжения позволяет измерять мощность до 12 ГВт в электрич. цепях с током до 15 кА и напря­жением до 500 кВ.

Техн. требования к В. стандартизо­ваны в ГОСТах 22261—76, 8476—60 и 1.3605—75.

• Электрические измерения, под ред. Е. Г. Шрамкова, М., 1972; Электрорадиоизмерения, М., 1976; Справочник по электроиз­мерительным приборам, 2 изд., Л., 1977.

В. П. Кузнецов.

ВАТТ-ЧАС (Вт•ч, W•h), внесистем­ная ед. работы и энергии, широко применяемая в технике. 1 Вт•ч=3600 Дж, 1 киловатт-час=3,6•10⁶ Дж.

ВЕБЕР (Вб, Wb), единица СИ магн. потока и потокосцепления. Назван в честь нем. физика В. Э. Вебера (W. Е. Weber). 1 Вб равен магн. по­току, создаваемому однородным магн. полем при индукции 1 тесла через нормальную к потоку площадку в 1 м². Другое определение: 1 Вб равен магн. потоку, при убывании к-рого до нуля в сцепленном с ним контуре сопротивлением 1 Ом через поперечное сечение проводника проходит кол-во электричества 1 Кл. 1 Вб=1 Кл•Ом=1 В•с=1 Т•м²=10⁸ максвелл. ВЕБЕРМЕТР (от вебер и греч. metreo — измеряю) (флюксметр), прибор для измерения потока магнитной ин­дукции. См. Флюксметр.

ВЕЙСА ИНДЕКСЫ, см. в ст. Ин­дексы кристаллографические.

ВЕКТОР СОСТОЯНИЯ, то же, что волновая функция.

ВЕКТОРНОГО ТОКА СОХРАНЕНИЕ в слабом взаимодействии, свойство сохранения векторного заряженного тока слабого вз-ствия адронов, вытекающее из сохранения электрич. тока и изотопической инвариантности сильного вз-ствия, (Из-за нарушения изотопич. инвариантности в сла­бом вз-ствии наблюдается небольшое, ~1%, отклонение от закона В. т. с.) Предсказано С. С. Герштейном и Я. Б. Зельдовичем (1955) и незави­симо от них амер. физиками Р. Фейнманом и М. Гелл-Маном (1957). В сла­бом вз-ствии В. т. с. аналогично за­кону сохранения электрич. заряда в эл.-магн. вз-ствии. Благодаря В. т. с. оказываются универсальными константы, характеризующие слабое векторное вз-ствие адронов (слабые векторные «заряды»): эти константы не изменяются (не перенормируются) под действием сильного вз-ствия, так же как не изменяются в результате сильного вз-ствия электрич. заряды адронов (напр., электрич. заряд про­тона в точности равен электрич. за­ряду позитрона, не обладающего силь­ным вз-ствием). Эти следствия В. т. с. были подтверждены в большом числе экспериментов (в -распаде -мезона: ⁺⁰+e⁺+v_e, в -распаде ядер, в нейтринных экспериментах и др.). При обобщении В. т. с. на векторные токи с изменением странности стано­вится существенным учёт эффектов нарушения унитарной симметрии, связанных с разностью масс странного (s) и нестранных (и, d) кварков. В. т. с. и аксиального тока частичное сохра­нение используются в формализме т. н. алгебры токов. См. также Киральная симметрия.

• См. лит. при ст. Аксиального тока частич­ное сохранение.

М. Ю. Хлопов.

ВЕКТОРНОЕ ПОЛЕ, поле физиче­ское, к-рое описывается ф-цией, яв­ляющейся в каждой точке пр-ва век­тором (или четырёхмерным вектором). Пример — векторный потенциал в электродинамике. В квант. теории поля квантом В. п. служит ч-ца со спином 1 (напр., фотон, гипотетич. глюоны и промежуточные векторные бозоны). В. п. меняет знак при прост­ранственной инверсии, т. е. ч-цы, соот­ветствующие В. п., имеют отрицат. внутр. чётность (и наз. векторными; к ним относятся фотон, -, -, -мезоны, - и Y- частицы и др.).

А. В. Ефремов.

ВЕКТОР-ПОТЕНЦИАЛ, см. Потен­циалы электромагнитного поля.

«ВЕЛИКОЕ ОБЪЕДИНЕНИЕ» ( «ве­ликий синтез») (Grand Unificaion), теоретические модели, исходящие из представлений о единой природе силь­ного, слабого и эл.-магн. вз-ствий. В основе этих моделей лежат обнару­женная симметрия между лептонами и кварками в единой теории эл.-магн. и слабого вз-ствий (в электрослабом вз-ствии, см. Слабое взаимодействие) и тот факт, что в калибровочных тео­риях поля предсказывается при пере­ходе к малым расстояниям (т. е. к вы­соким энергиям), с одной стороны, увеличение константы электрослабого вз-ствия, а с другой — уменьшение константы сильного вз-ствия (см. Квантовая хромодинамика). Экстра­поляция такой тенденции на сверхвысокие энергии приводит к равенству констант всех трёх вз-ствий при нек-ром энергетич. масштабе . В моделях «В. о.» предполагается, что при энер­гиях ξ> глюоны, фотоны, проме­жуточные векторные бозоны W^± и Z⁰ явл. квантами калибровочных по­лей единой калибровочной симметрии «В. о.». Кроме того, объединение леп­тонов и кварков в единые мультиплеты группы симметрии «В. о.» приводит к существованию довольно большого числа смешанных калибровочных по­лей (с той же константой вз-ствия), кванты к-рых обладают одновременно лептонным и «цветовым» зарядами. Величина Л характеризует энергетич. масштаб спонтанного нарушения сим­метрии «В. о.», за счёт к-рого воз­никают массы у ч-ц, описывающих смешанные калибровочные поля. В разных моделях «В. о.» предсказы­вается разл. величина . В большин­стве моделей ~10¹⁴—10¹⁶ ГэВ (од­нако существуют модели и «раннего» «В. о.» при ~10⁶—10⁸ ГэВ). Такие энергии недостижимы ни на плани­руемых в обозримом будущем уско­рителях, ни в косм. лучах, так что для проверки моделей «В. о.» могут использоваться либо предсказания мо­делей в низкоэнергетич. области, либо их космологич. следствия [по совр. представлениям, на очень ранних ста­диях расширения Вселенной могли достигаться темп-ры (в энергетич. шкале) Т].

В рамках «В. о.» однозначно опре­деляется величина параметра sin²_W (где _W— т. н. угол Вайнберга) тео­рии электрослабого вз-ствия, харак­теризующего вз-ствие нейтральных слабых токов (см. Нейтральный ток). Этот параметр определяется при ξ> структурными постоянными группы симметрии «В. о.», а при низких энер­гиях ξ<<, отвечающих условиям совр. экспериментов, его величина вычисляется с помощью процедуры перенормировки.

В большинстве моделей объедине­ние кварков и лептонов приводит к существованию кварк-лептонных переходов с несохранением барионного заряда. Такие переходы могут вызывать распады протона. Модели «В. о.» предсказывают, что время жизни протона должно составлять 10³⁰ — 10³² лет. Несохранение барионного заряда может иметь также важ­ные космологич. следствия: неравно­весные процессы с нарушениями СР-инвариантности (см. Комбинирован­ная инверсия) и закона сохранения барионного заряда в ранней Вселен­ной могут объяснить наблюдаемую барионную асимметрию Вселенной (т. е. отсутствие заметного кол-ва ан­тибарионов во Вселенной). В моде­лях «В. о.» возникают определ. со­отношения между массами кварков и

69


лептонов. В рамках моделей «В. о.» может найти естеств. объяснение ма­лая ненулевая масса покоя нейтрино. Неизбежным следствием всех суще­ствующих моделей «В. о.» явл. кван­тование электрич. заряда и существо­вание решений типа магнитных монополей Дирака. При этом масса монополей оказывается очень большой, ~/ (где  — безразмерная кон­станта эл.-магн. вз-ствия), так что они не могут образовываться в совре­менных лаб. или косм. условиях. Космологич. оценки концентрации монополей, образовавшихся в ранней Вселенной, дают величину, значи­тельно превышающую существующие наблюдат. ограничения, что создаёт серьёзную проблему для космологии и моделей «В. о.». Величина А в моде­лях «В. о.» близка к величине т. н. планковской массы m_П~10¹⁹ ГэВ, при к-рой становится необходимым пере­ход к квант. описанию гравитацион­ного взаимодействия. Это позволяет надеяться, что дальнейшее развитие моделей «В. о.» приведёт к объеди­нению всех фундам. вз-ствий, вклю­чая и гравитационное.

• Окунь Л. Б., Современное состояние и перспективы физики высоких энергий, «УФН», 1981, т. 134, в. 1, с. 3.

М. Ю. Хлопов.

ВЕНТУРИ ТРУБКА (расходомер Вентури), устройство для замера расхода или скорости жидкостей и газов в тру­бопроводах. Предложена итал. учё­ным Дж. Вентури (G. Venturi). Пред­ставляет собой сужение на трубопро­воде, где скорость возрастает, а давле­ние соотв. уменьшается. Если через d₁ p₁ v₁ и d₂, р₂, v₂ обозначить диа­метр, давление и скорость соотв. во входном 1 и в самом узком 2 сече­ниях В. т., то



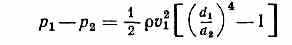
( — плотность жидкости).

По заданным размерам В. т. и изме­ренной с помощью дифф. манометра разности давлений р₁-p₂ из данного равенства можно определить ср. ско­рость v₁ а следовательно, и расход.

А. Д. Альтшуль.

ВЕРДЕ ПОСТОЯННАЯ (удельное маг­нитное вращение), характеризует магн. вращение плоскости поляризации света в в-ве (см. Фарадея эффект). Названа по имени франц. математика М. Верде (М. Verdet), наиболее полно исследо­вавшего законы магн. вращения. Оп­тически неактивное в-во, помещённое в магн. поле (или имеющее собств. магн. момент), поворачивает плос­кость поляризации света, распростра­няющегося в нём вдоль направления поля. Для немагн. в-ва, помещённого в поле, угол поворота =VlH (з а к о н Верде), где l — длина пути луча в в-ве в м (или см), Н — напря­жённость магн. поля в А/м (или в Э), V — В. п. в рад/А [или рад/(Э•см)].

В. п. зависит от длины волны света (вращательная диспер­сия), плотности в-ва и слабо — от его темп-ры Т. Для большинства в-в V>0 (правовращающие в-ва), лишь для нек-рых V<0 (левовращающие в-ва, напр. парамагн. соли железа). В последнем случае температурная зави­симость сильнее (V~T^-1). Значения V обычно невелики (0',01—0',02); сравнительно большие значения имеет сероуглерод, нек-рые сорта стекла (F~0',04-0',09).

Магн. вращением обладают все тела, хотя обычно в слабой степени. Осо­бенно велики значения угла враще­ния для ферромагн. металлов. Однако это происходит не за счёт больших значений V; для них вращение растёт пропорц. магн. индукции, а не напря­жённости поля, поэтому в ф-ле, опре­деляющей 6, нужно заменить Н магн. индукцией В.

Наряду с В. п. пользуются величи­ной т. н. молекулярного вращения = V/, где  — плот­ность в-ва в моль/м³ (или моль/см³), либо т. н. молекулярной по­стоянной магнитного вращения D = 9n/(n²+2), где n — показатель преломления в-ва. Для величины D характерно то, что она, подобно удельной рефракции, сохра­няет своё значение при изменениях плотности и агрегатного состояния в-ва и часто обладает св-вом аддитив­ности.

• См. лит. при ст. Фарадея эффект.