Вавилова закон

Вид материала

Закон

Содержание Вероятность квантового пере­хода P=mg, где m — масса тела, g — Рис. 1. Схема равноплечных рычажных ве­сов: О — точка опоры коромысла А В; С и р Гука закон. Рис. 4. Схема крутильных (торсионных) ве­сов: 1 — спиральные пружины; 2 — рычаг для помещения нагрузки; 3 — магн. успо­коитель; Гидро­статическое взвешивание). Вечный двигатель Взаимная индуктивность Кирхгофа закон излучения И. Г. Кондратьев, М. А. Миллер. Взаимодействие ультразвука с электронами проводимо­сти Н. А.Смирнова.

Подобный материал:

• Н. И. Вавилова аналитический отчет, 217.51kb.
• Урок по общей биологии в 11 классе «Дело академика Вавилова», 851.64kb.
• Селекция- одомашнивание, 126.51kb.
• Уважаемые коллеги!, 64.43kb.
• Українське товариство генетиків І селекціонерів ім. М.І. Вавилова, 45.97kb.
• «Саратовский государственный аграрный университет имени Н. И. Вавилова», 377.27kb.
• Саратовский Государственный Аграрный Университет им. Н. И. Вавилова. Кафедра Акушерства, 248.61kb.
• О. Б. Ширяев Институт общей физики ран, 119991, Москва, ул. Вавилова,, 20.28kb.
• Главное управление образования, 70.84kb.
• Издательский дом, 529.99kb.

ВЕРОЯТНОСТЬ КВАНТОВОГО ПЕРЕ­ХОДА, величина, обратная времени жизни квант. системы по отношению к данному квант. переходу (см. Кван­товый переход).

ВЕРОЯТНОСТЬ ТЕРМОДИНАМИЧЕ­СКАЯ, число способов, к-рыми может быть реализовано данное состояние макроскопич. физ. системы. В термо­динамике состояние физ. системы ха­рактеризуется определ. значениями плотности, давления, темп-ры и др. измеряемых величин. Перечисленные величины определяют состояние сис­темы в целом (её макросостояние). Однако при одной и той же плотно­сти, темп-ре и т. д. ч-цы системы могут находиться в разных местах её объёма и иметь разл. значения энергии или импульса. Каждое состояние физ. си­стемы с определ. распределением её ч-ц по возможным классич. или квант. состояниям наз. микросостоя­нием. В. т. W равна числу микро­состояний, реализующих данное мак­росостояние, из чего следует, что W1. Её легко вычислить лишь в слу­чае идеальных газов. Для реальных систем В. т. можно оценить по вели­чине статистической суммы,. В. т. свя­зана с энтропией S системы соотно­шением Больцмана: S=klnW. В. т. не явл. вероятностью в матем. смысле (последняя 1); применяется в ста­тистической физике для вычисления св-в системы, находящейся в термодинамич. равновесии (для равновесного состояния В. т. имеет макс. зна­чение). Для расчёта В. т. сущест­венно, считаются ли одинаковые ч-цы системы различимыми или неразличи­мыми. Поэтому классич. механика и квант. механика приводят к разным выражениям для В. т.

ВЕС, численная величина силы тя­жести, действующей на тело, нахо­дящееся вблизи земной поверхности: P=mg, где m — масса тела, g — ус­корение свободного падения (или ус­корение силы тяжести). Поскольку масса тела — величина постоянная, а значение g изменяется на Земле с широтой и высотой над ур. м. (со­ответствующую ф-лу см. в ст. Ускоре­ние свободного падения), то соотв. при этом изменяется и В. тела. Из­меряется В. тела в ед. силы (Н, кгс, дин и др.).

ВЕСЫ, прибор для определения массы тел по действующей на них силе тя­жести. В. иногда наз. также приборы для измерений др. физ. величин, пре­образуемых с этой целью в силу или в момент силы. К таким приборам от­носятся, напр., токовые весы и кру­тильные весы. В научных исследова­ниях применяют аналитич., микроаналитич., пробирные и др. типы точ­ных В. Последовательность действий при определении массы тел на В. рассмотрена в ст. Взвешивание.

В зависимости от назначения В. де­лятся на образцовые (для поверки гирь), лабораторные (в т. ч. аналити­ческие) и общего назначения. По принципу действия В. подразделяются на рычажные, пружинные, крутиль­ные, электротензометрич., гидростатич., гидравлические.

Наиболее распространены рычаж­ные В., их действие основано на законе равновесия рычага. Точка опо­ры рычага («коромысла» В.) может находиться посередине (равноплечные В.) или быть смещённой относи­тельно середины (неравноплечные и одноплечные В.). Многие рычажные В. представляют собой комбинацию рычагов 1-го и 2-го родов. Опорами рычагов служат обычно призмы и подушки из спец. сталей или тв. кам­ня (агат, корунд). На равноплечных рычажных В. взвешиваемое тело уравновешивается гирями, а нек-рое превышение (обычно на 0,05—0,1%) массы гирь над массой тела (или наобо­рот) компенсируется моментом, созда­ваемым коромыслом (со стрелкой) из-за смещения его центра тяжести относительно первонач. положения (рис. 1). Нагрузка, компенсируемая смещением центра тяжести коромысла, измеряется при помощи отсчётной шкалы. Цена деления s шкалы ры­чажных В. определяется ф-лой: s= k(P₀c/lg), где Р₀ — вес коромысла со стрелкой, с — расстояние между центром тяжести коромысла и осью его вращения, l — длина плеча коро­мысла, g — ускорение свободного па­дения, k — коэфф., зависящий только от разрешающей способности отсчёт-

70


ного устройства. Цену деления, а сле­довательно и чувствительность В., можно в определённых пределах из­менять (обычно за счёт перемещения спец. грузика, изменяющего расстоя­ние с).

В ряде рычажных лаб. В. часть измеряемой нагрузки компенсируется силой эл.-магн. вз-ствия — втягива­нием железного сердечника, соеди­нённого с плечом коромысла, в не­подвижный соленоид. Ток в соле­ноиде регулируется электронным уст­ройством, приводящим В. к равнове­сию. Измеряя ток, определяют про­порциональную ему нагрузку В.



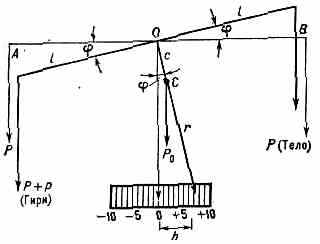
Рис. 1. Схема равноплечных рычажных ве­сов: О — точка опоры коромысла А В; С и р₀ — центр тяжести и вес коромысла со стрелкой; ОС=с — расстояние между точ­кой опоры и центром тяжести коромысла; Р — вес тела; р — перегрузок, уравнове­шиваемый смещением центра тяжести коро­мысла; r — длина стрелки; h — отклонение стрелки.




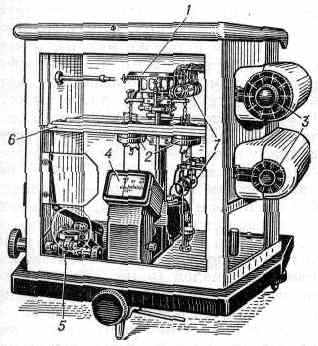
Рис. 2. Равноплечные двухчашечные микро-аналитич. весы (предельная нагрузка 20 г): 1 — коромысло; 2 — возд. успокоители; 3 — механизмы наложения встроенных гирь (от 1 до 999 мг); 4 — проекц. шкала отсчёта; 5 — манипулятор, выдвигающий чашку ве­сов в окошко; 6 — перегородка, защищаю­щая коромысло от температурных влияний и возд. потоков; 7 — встроенные гири, име­ющие форму колец.


В лаб. практике всё шире приме­няются В. (в особенности аналитиче­ские) со встроенными гирями на часть нагрузки или на полную нагрузку (рис. 2). Принцип действия таких В. был предложен Д. И. Менделеевым. Гири спец. формы подвешиваются к плечу, на к-ром находится чашка для

нагрузки (одноплечные В.), или (реже) на противоположное плечо. В одно-плечных В. (рис. 3) полностью исклю­чается погрешность из-за неравноплечности коромысла.

Совр. лабораторные В. (аналитиче­ские и др.) снабжаются рядом уст­ройств для повышения точности и скорости взвешивания: успокоителями ко­лебаний коромысла (воздушными или магнитными); дверцами, при откры­тии к-рых почти не возникает потоков воздуха; тепловыми экранами; меха­низмами наложения и снятия встроен­ных гирь; автоматически действующи­ми механизмами для подбора встроен­ных гирь при уравновешивании В.



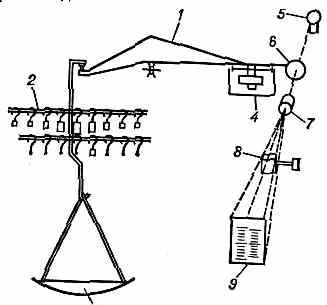
Рис. 3. Схема одноплечных аналитич. весов: 1 — коромысло; 2 — встроенные гири; а — грузоприёмная чашка; 4 — противовес и успокоитель; 5 — источник света; 6 — про­екц. шкала; 7 — объектив; 8 — устройство для коррекции нуля: 9 — экран.


Применяются проекц. шкалы, по­зволяющие повысить точность отсчёта по шкале при малых углах отклоне­ния коромысла. Про принципу ры­чажных В. устроено большинство ти­пов метрологич., образцовых, анали­тич., техн., торговых, медицинских и др. В.

В основу действия пружинных и электротензометрич. В. положен Гука закон. Чувствит. элементом в пружинных В. явл. пружина, де­формирующаяся под действием веса тела. Показания В. отсчитывают по шкале, вдоль к-рой перемещается со­единённый с пружиной указатель. При­нимается, что после снятия нагрузки указатель возвращается в нулевое положение, т. е. в пружине под дей­ствием нагрузки не возникает оста­точных деформаций. При помощи пру­жинных В. измеряют не массу, а вес. Однако в большинстве случаев шкала пружинных В. градуируется в ед. массы. Вследствие зависимости ускорения свободного падения от географич. широты и высоты над ур. м., показания пружинных В. зависят от места их нахождения. Кроме того, упругие св-ва пружины зависят от темп-ры и меняются со временем; всё это снижает точность пружинных В.

В крутильных (торсионных) В. чувствит. элементом служит упругая нить или спиральные пружины (рис. 4). Нагрузка опреде­ляется по углу закручивания нити (пружины), к-рый пропорционален со­здаваемому нагрузкой крутильному моменту.

Действие электротензометрических В. основано на преобразовании деформации упругих



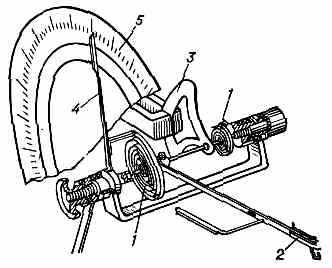
Рис. 4. Схема крутильных (торсионных) ве­сов: 1 — спиральные пружины; 2 — рычаг для помещения нагрузки; 3 — магн. успо­коитель; 4 — стрелка; 5 — шкала.


элементов (столбиков, пластин, ко­лец), воспринимающих силовое воз­действие нагрузки, в изменение электрич. сопротивления. Преобразовате­лями служат высокочувствительные проволочные тензометры, приклеен­ные к упругим элементам (см. Пьезо­электрический преобразователь). Как правило, электротензометрич. В. при­меняются для взвешивания больших масс. !

Гидростатические В. слу­жат гл. обр. для определения плот­ности тв. тел и жидкостей (см. Гидро­статическое взвешивание).

Гидравлические В. по уст­ройству аналогичны гидравлич. прес­су. Отсчёт показаний производится по манометру, градуированному в ед. массы.

Все типы В. характеризуются: пре­дельной нагрузкой — наибольшей статич. нагрузкой, к-рую могут выдер­живать В. без нарушения их метроло­гич. хар-к; ценой деления — значе­нием массы, соответствующим изме­нению показания на одно деление шкалы; пределом допускаемой по­грешности взвешивания — наиболь­шей допускаемой разностью между результатом одного взвешивания и действит. массой взвешиваемого тела; допускаемой вариацией показаний — наибольшей допускаемой разностью показаний В. при неоднократном взве­шивании одного и того же тела.

• Рудо Н. М., Весы. Теория, устройство, регулировка и проверка, М.— Л., 1957; Маликов Л. М., Смирнова Н. А., Ана­литические электрические весы, в кн.: Энцик­лопедия измерений, контроля и автоматиза­ции, в. 1, М.— Л., 1962; Гаузнер С. И., М и х а и л о в с к и й С. С., О р л о в В. В., Регистрирующие устройства в автоматиче­ских процессах взвешивания, М., 1966; С а р а х о в А. И., Весы в физико-химических исследованиях, М., 1968.

Н. А. Смирнова.

71


ВЕЧНЫЙ ДВИГАТЕЛЬ (перпетуум-мобиле) (лат. perpetuum mobile, букв.— вечно движущееся), вообра­жаемый двигатель, к-рый, будучи раз пущен в ход, совершал бы работу неограниченно долгое время, не за­имствуя энергию извне (так называе­мый В. д. 1-го рода). Идея В. д. 1-го рода противоречит закону сохранения и превращения энергии (см. Энергии сохранения закон) и неосуществима. Возможность работы такого двигателя неогранич. время означала бы полу­чение энергии из ничего. Первые проекты механич. В. д. относятся к 13 в. (Виллар де Синекур, 1245, Пьер де Марикур, 1269, Франция). К кон. 18 в., вследствие бесплодности мно­говековых попыток осуществления В.д., среди учёных укрепилось убеж­дение в невозможности его создания, и с 1775 Парижская АН отказалась рассматривать проекты В. д. В сер. 19 в. с установлением закона сохра­нения и превращения энергии была доказана принципиальная неосущест­вимость В. д. Среди предложенных моделей В. д. наиб. распространены механические, в к-рых к.-л. массивное тело перемещается по замкнутому пути. На одних его участках (при опускании) тело совершает работу, на других для перемещения тела (подъёма вверх) необходима затрата анергии. Такие механизмы могут со­вершать работу лишь за счёт первонач. запаса кинетич. энергии, сооб­щённого им при пуске; когда этот запас оказывается израсходованным, В. д. останавливается. В более слож­ных проектах В. д. механич. энергия превращается в др. виды энергии (электрич., тепловую и т. п.). Наряду с В. д. 1-го рода рассматривают В. д. 2-го рода — воображаемую периоди­чески действующую машину, к-рая целиком превращала бы в работу теп­лоту, извлекаемую из окружающих тел (океана, атм. воздуха и др.). При этом должна уменьшаться суммарная энтропия среды и В. д., что противо­речит второму началу термодинамики. От В. д. следует отличать «мнимые» В. д.— механизмы, работающие за счёт природных запасов энергии (сол­нечной, внутриатомной и др.). Такие механизмы могут работать очень дол­го, до механич. износа деталей, но считать их В. д. нельзя.

• Планк М., Принцип сохранения энер­гии, пер. с нем., М.— Л., 1938; Кудряв­цев П. С., История физики, т. 2, М., 1956.

ВЕЩЕСТВО, вид материи, обладаю­щей массой покоя. В конечном счёте В. слагается из элем. ч-ц, масса покоя к-рых не равна нулю (в осн. из эл-нов, протонов и нейтронов). В классич. физике В. и поле физическое противо­поставлялись друг другу как два вида материи, у первого из к-рых структура дискретна, а у второго — непрерывна. Квант. физика, внедрившая идею двойственной корпускулярно-волновой природы любого мик­рообъекта (см. Корпускулярно-волновой дуализм), привела к нивелирова­нию этого представления. Выявление тесной взаимосвязи В. и поля при­вело к углублению представлений о структуре материи. На этой основе были строго разграничены понятия В. и материи, отождествлявшиеся в нау­ке на протяжении многих веков.

И. С. Алексеев.

ВЗАИМНАЯ ИНДУКТИВНОСТЬ, см. Индуктивность взаимная.

ВЗАИМНАЯ ИНДУКЦИЯ, см. Ин­дукция взаимная.

ВЗАИМНОСТИ ПРИНЦИП (взаимно­сти теорема), устанавливает пере­крёстную связь между двумя источ­никами и создаваемыми ими полями в местах расположения источников для одной и той же линейной системы (среды). В. п. выполняется для разно­образных систем (механич., электрич., акустич., магнитных и др.), описы­ваемых широким классом линейных дифф. и разностных ур-ний (Лапласа, Гельмгольца, волновым, диффузии, Клейна — Гордона и пр.). Впервые В. п. был сформулирован нем. учё­ным Г. Гельмгольцем (1860), а затем обобщён англ. физиком Дж. У. Рэлеем (1873) и голл. физиком X. Ло­ренцем (1896).

Согласно В. п., если металлич. тело, несущее пост. электрич. заряд Q₁,создаёт на втором изолированном ме­таллич. теле потенциал ₁₂, то, если придать второму телу заряд Q₂, со­здаваемый им потенциал на свобод­ном от заряда первом теле ₂₁ будет равен:

₂₁=₁₂Q₂/Q₁. (1)

Для двух электрич. диполей с момен­тами 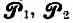и создаваемых ими в ди­электрике электрич. полей E₁₂, E₂₁ В. п. выражается соотношением: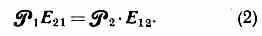



Ф-ла (2) справедлива и для полей, гармонически изменяющихся во вре­мени, если только под 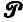и Е подра­зумевать их комплексные амплитуды. В общем случае источников эл.-магн. поля, задаваемых через плотности перем. токов j₁ и j₂, В. п. записы­вается в интегр. форме: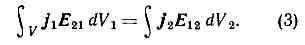



Соотношения (2), (3) несправедливы для гиротропных сред (плазма в магн. поле, ферриты), однако ими можно пользоваться, если источники зада­вать в разных средах, отличающихся направлением внеш. магн. поля.

В. п. позволяет обобщить Кирхгофа закон излучения о связи излучат. и поглощат. способностей на произволь­ные электродинамич. системы. Из В. п. следует, в частности, совпаде­ние диаграмм направленности антен­ны в режимах передачи и приёма. Теорема Шокли — Рамо о токах, наводимых на электродах движущимся зарядом, была первым применением В. п. в электронике. В теории ли­нейных цепей В. п. (при перестановке эдс из одной ветви цепи в другую в первой ветви получается тот же ток, что тёк ранее во второй) помогает расшифровать структуры сложных це­пей разной природы.

• Фурдуев В. В., Теоремы взаимности в механических, акустических и электроме­ханических четырехполюсниках, М.— Л., 1948; Вайнштейн Л. А., Электромаг­нитные волны, М., 1957; М о р с Ф. М., Ф е ш б а х Г., Методы теоретической физи­ки, пер. с англ., т. 1—2, М., 1958—60.

И. Г. Кондратьев, М. А. Миллер.

ВЗАИМОДЕЙСТВИЕ в физике, воз­действие тел или ч-ц друг на друга, приводящее к изменению состояния их движения. В механике Ньютона взаимное действие тел друг на друга количественно характеризуется си­лой. Более общей хар-кой В. явл. потенц. энергия. Первоначально в фи­зике утвердилось представление о том, что В. между телами может осуществ­ляться непосредственно через пустое пр-во, к-рое не принимает участия в передаче В., передача В. происхо­дит мгновенно. Так, считалось, что перемещение Земли должно сразу же приводить к изменению силы тяготе­ния, действующей на Луну. В этом состояла т. н. концепция дально­действия. Эти представления были оставлены как не соответствующие дей­ствительности после открытия и ис­следования эл.-магн. поля. Было до­казано, что В. электрически заряж. тел осуществляется не мгновенно и перемещение одной заряж. ч-цы приво­дит к изменению сил, действующих на др. ч-цы, не в тот же момент, а лишь спустя конечное время. Каждая элект­рически заряж. ч-ца создаёт эл.-магн. поле, действующее на др. ч-цы, т. с. В. передаётся через «посредника» — эл.-магн. поле. Скорость распростра­нения эл.-магн. поля равна скорости света в пустоте: 300 000 км/с. Воз­никла новая концепция — концепция близкодействия, к-рая затем была распространена и на любые др. В. Согласно этой концепции, В. между телами осуществляется посредством тех или иных полей (напр., тяготение — посредством гравитац. поля), непре­рывно распределённых в пр-ве.

После появления квант. теории поля представление о В. существенно изме­нилось. Согласно этой теории, любое поле явл. не непрерывным, а имеет дискр. структуру. Вследствие корпускулярно-волнового дуализма, каж­дому полю должны соответствовать определ. ч-цы. Так, заряж. ч-цы не­прерывно испускают и поглощают фо­тоны, к-рые и образуют окружающее их эл.-магн. поле. Эл.-магн. В. в квант. теории поля явл. результа­том обмена ч-ц фотонами — квантами эл.-магн. поля, т. е. фотоны явл. переносчиками этого В. Аналогично др. виды В. возникают в результате обмена ч-ц квантами соответствующих полей (см. Квантовая теория поля).

72


Несмотря на разнообразие воздей­ствий тел друг на друга (зависящих от В. слагающих их элем. ч-ц), в при­роде, по совр. данным, имеется лишь четыре типа фундам. В. Это (в по­рядке возрастания интенсивности В.): гравитационное В., слабое взаимо­действие, электромагнитное взаимо­действие, сильное взаимодействие. Ин­тенсивности В. определяются кон­стантами связи (в частности, для эл.-магн. В. константой связи явл. электрич. заряд).

Совр. квант. теория эл.-магн. В. превосходно описывает все известные эл.-магн. явления. В 60—70-х гг. в осн. построена единая теория сла­бого и эл.-магн. вз-ствий (т. н. электро­слабое В.) лептонов и кварков. Совр. теорией сильного В. явл. квантовая хромодинамика. Делаются попытки объединения электрослабого и силь­ного В. (т. н. «Великое объединение»), а также включения в единую схему гравитац. В.

• Григорьев В. И., Мякишев Г.Я , Силы в природе, 5 изд., М., 1977. См. также лит. при ст. Поля физические и Квантовая

ВЗАИМОДЕЙСТВИЕ УЛЬТРАЗВУКА С ЭЛЕКТРОНАМИ ПРОВОДИМО­СТИ, см. Акустоэлектронное взаимо­действие.

ВЗВЕШИВАНИЕ, определение массы тел при помощи весов. Высокая точ­ность при В. достигается учётом всех возможных погрешностей весов, гирь, применяемого метода В., а также по­грешностей, обусловленных влиянием внеш. условий (действием аэростатич., электрич. и магн. сил, колебаниями темп-ры и влажности воздуха и др.).



Пределы допускаемых погрешностей весов разных типов и гирь приведены в ст. Весы и Гири. При В., не требую­щем высокой точности (когда не учи­тывается влияние аэростатич. и др. сил), обычно пользуются методом прямого В.: масса тела прини­мается равной алгебр. сумме масс гирь, уравновешивающих тело, и по­казаний отсчётного устройства весов. В этом случае в результат В. на равно-плечных весах полностью входит по­грешность из-за неравноплечности ко­ромысла. Более высокая точность при прямом В. достигается на одноплечных весах, исключающих эту погреш­ность, т. к. взвешиваемое тело и

уравновешивающие его гири нахо­дятся на одном и том же плече коро­мысла. Для исключения погрешностей из-за неравноплечности коромысла при В. на равноплечных весах применяют т. н. методы точного В. Метод замещения (метод Борда) за­ключается в том, что после уравновешивания тела тарным грузом (обрез­ками металла, дробью и т. п.), поме­щённым на другом плече коромысла, тело снимают с весов и на его место помещают гири в таком кол-ве, чтобы привести весы в положение, близкое к исходному положению равновесия. Массу взвешиваемого тела определяют по массе гирь и по показанию весов, соответствующему неуравновешенной гирями части массы. В методе Д.И. Менделеева на одну из ча­шек помещают гири в кол-ве, соответ­ствующем предельной нагрузке весов, а на другую чашку — тарный груз, уравновешивающий гири. Взвешивае­мое тело помещают на чашку с ги­рями, снимая при этом столько гирь, чтобы весы пришли в положение, близкое к исходному положению рав­новесия. Массу взвешиваемого тела определяют по массе снятых гирь и по показанию весов. Метод двой­ного В. (метод Гаусса) состоит в повторном прямом В. после переста­новки тела и гирь с одной чаш­ки весов на другую. Масса тела М=¹/₂(М₁+М₂), где М₁ и М₂ — результаты двух прямых В.

По точности все три метода равно­ценны. Выбор метода зависит от конструкции весов и условий В. При

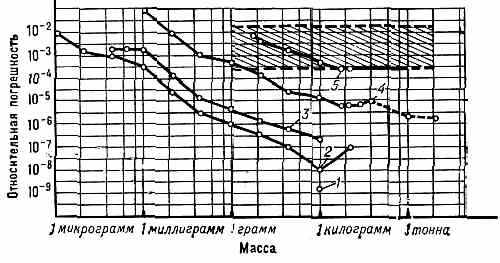
Хар-ки точности измерений массы в зависимости от её величины и мето­да измерения: 1 — сличения гос. эталона ед. массы (килограмма); 2 — метрологич. исследова­ния; 3 — аналитич. ис­следования высшей точ­ности; 4 — технич. взве­шивания повыш. точно­сти, взвешивания драго­ценных металлов; 5 — торговые и хозяйствен­ные взвешивания; за­штрихованная область — взвешивание на автоматич., крановых и др. технологич. весах и доза­торах.

особо точных В. не только приме­няют методы точного В., но и учиты­вают погрешности гирь. Для упро­щения оценки погрешности, обуслов­ленной влиянием аэростатич. сил, возникающих из-за неравенства объ­ёмов взвешиваемого тела и гирь (см. Архимеда закон), для всех гирь, за исключением эталонных, принимают условную плотность материала, рав­ную 8,0•10³ кг/м³ (независимо от того, из какого материала они из­готовлены). В принципе В. (опреде­ление массы) может быть осуществ­лено на основе любого физ. эффекта, объединяющего силовое или инер­ционное проявление массы с изменением к.-л. физ. величины (электрич. тока, магн. поля, оптич. характерис­тик в-в и т. д.). На рисунке графи­чески показаны достигнутые точности взвешиваний в разл. областях науки, техники и нар. х-ва.

• Рудо Н. М., Лабораторные весы и точ­ное взвешивание, М., 1963; Смирнова Н. А., Единицы измерений массы и веса в Международной системе единиц, М., 1966.

Н. А.Смирнова.