Geum.ru

Учебно-методический комплекс Специальность: 080505 Управление персоналом Москва 2009

Вид материалаУчебно-методический комплекс

Содержание


Тематика контрольных работ и методические указания по их выполнению (для заочной формы обучения)
Итого ($)
Итого ($)
Общая прибыль
Хз1 +х32+хзз+х34=280
=суммпройзв( в12:е15; в4:е7)
Суммпроизв(в12:е15; в4:е7) = b12*b4+c12*c4+d12*d4+e12*e4+ b13*b5+c13*c5+d13*d5+e13*e5+ b14*b6+c14*c6+d14*d6+e14*e6+ b15*b7+c15*c
Общее количество продавцов
Подобный материал:
1   2   3   4   5

Тематика контрольных работ и методические указания по их выполнению (для заочной формы обучения)



Задание 1. Использование сверхурочных работ

При изготовлении изделий двух видов осуществляется последовательная обработка соответствующих заготовок на двух различных станках. Каждый станок может использоваться для производства изделий по 8 часов в сутки, однако этот фонд времени можно увеличить на 4 часа за счет сверхурочных работ. Каждый час сверхурочного времени требует дополнительных расходов: для станка 1 это долл.5, для станка 2 — долл.7. Производительность станков и продажная цена изделий приведены в таблице.

Станок
Производительность станков (изделие/ч)




изделие 1
изделие 2

1
5
6

2
4
8

Цена изделия
$6
$4


Требуется определить объемы производства изделий каждого вида и уровень использования сверхурочного времени на каждом из станков, обеспечивающие получение максимальной прибыли.

Содержимое изменяемых ячеек

Определим X11, Х12 как количества изделий первого типа, выпускаемых соответственно на первом и втором станках. Аналогично,

Х21, Х22 будут определять количество изделий второго типа, выпускаемых на этих же станках.

Т1с/у, Т2с/у — время сверхурочных работ соответственно на первом и втором станках.

Ограничения

1. По времени занятости станков:

XI1/5 + Х21/6 <= 8 + Tlc/y; X12/4 + Х22/8 <= 8 + Т2с/у; Т1с/у <= 4; Т2с/у <= 4.

2. «Естественные» ограничения:

Tlc/y >м 0; Т2с/у >= 0; Х11+Х22 >= 0. Целевая функция:

Z = (Х11+ Х12)*6 + (Х21 + Х22)*4 - (5*Т1с/у + 7*Т2с/у). Максимизировать Z.

Изменяемые ячейки: D3:E4; C10:Cll.

Ограничение по времени использования станков: С10:С11=Е10:Е11.

Целевая ячейка: G13.
A
В
С
D
E
F
G

1
Станок
Производительность станков (изделие/час)
Количество произведенных изделий по станкам (шт)






2



Изделие 1
Изделие 2
Изделие 1
Изделие 2






3
1
5
6












4
2
4
8












5



Цена изделия ($)
Общее количество изделий (шт)
Выручка за произведенные изделия ($)

6



6
4
=D3+D4
=ЕЗ+Е4
=B6*D6
=С6*Е6

7












ИТОГО ($)
=F6+G6

8
Станок
Время, связанное с производством изделий (час)
Издержки, связанные с использованием с/у времени ($)

9
Рабочее
Сверхурочное
Общий ресурс времени
Максимальное сверхурочное
Стоимость часа с/у времени ($)



10
1
8



=В10+С10
4
5
=C10*F10

11
2
8



=ВП+С11
4
7
=C11*F11

12












ИТОГО ($)
=G10+Gll

13









Общая прибыль
=G7-G12



Задание 2. Модель производства с запасами

Фирма переводит свой завод на производство новых изделий, которые планируется выпускать в течение четырех месяцев. Оценки спроса на изделия в каждый из этих месяцев приведены в таблице:


Месяц поставки изделия
1
2
3
4

Спрос (шт.)
100
200
180
300


В каждый месяц спрос можно удовлетворить за счет:
  • избытка изделий, произведенных в предшествующие месяцы;
  • изделий, произведенных в текущем месяце;
  • изделий, произведенных в последующие месяцы для погашения невыполненных ранее заказов.

Затраты на изготовление одного изделия составляют долл.4. Изделие, произведенное, но не поставленное потребителю в текущем месяце, влечет за собой дополнительные издержки на хранение в размере долл.0,5 за каждый месяц хранения. Изделие, выпускаемое в счет невыполненных заказов, облагается штрафом в размере долл.2 за каждый месяц недопоставки.

Объем производства меняется от месяца к месяцу по внутризаводским причинам. В рассматриваемые 4 месяца планируется следующая программа выпуска изделий.


Месяц производства изделия
1
2
3
4

Выпуск (штук)
50
180
280
270


Требуется уточнить (доопределить) эту программу таким образом, чтобы она обеспечивала минимальные издержки, обусловленные несогласованностью спроса и предложения (дисбалансом).

Задачи такого типа в исследовании операций известны как «транспортные задачи». Это обусловлено тем, что чаще всего такие задачи связаны с оптимизацией процессов перевозок. Вместе с тем к этому типу сводится рассматриваемая задача и многие другие, не имеющие непосредственного отношения к транспорту. Специфика этих задач заключается в использовании таблицы-матрицы, строки и столбцы которой определяют факторы дисбаланса — спрос и предложение, место производства и потребления продукции и т. п.

Пусть i определяет месяц производства изделия, a j — месяц поставки. В качестве содержимого изменяемых ячеек будем использовать Xij — количество изделий, произведенных в i-ый месяц и поставленных в j-ый.


Месяц производства (i)
Месяц потребления (j)
Программа выпуска изделий

1
2
3
4

1
4
4,5
5
5,5
50

2
6
4
4,5
5
180

3
8
6
4
4,5
280

4
10
8
6
4
270

Спрос (шт.)
100
200
180
300





В таком же виде определим программу производства изделий.


Месяц производства (i)
Месяц потребления (j)
Программа выпуска изделий

1
2
3
4

1















2















3















4
















Ограничения:

предложение (объемы производства):

ХИ+Х12+Х13+Х14= 50;

Х21 +Х22+Х23+Х24= 180;

ХЗ1 +Х32+ХЗЗ+Х34=280;

Х41+Х42+Х43+Х44=270.

спрос:

Х11+Х21+Х31+Х41=100;

X12+Х22+Х32+Х42=200;

Х13+Х23+ХЗЗ+Х43=180;

Х14+Х24+Х34+Х44=300.

Целевая функция:

Z= Sj Z, (XifCij) для i= 1,2,3,4; j= 1,2,3,4.

Минимизировать Z.

Структура ЭТ
A
B
C
D
E
F

1
Затраты на производство, хранение и штрафы (S)



2
Месяц производства
Месяц потребления
Программа выпуска изделий(шт.)

3



1
2
3
4

4
1
4
4,5
5
5,5
50

5
2
6
4
4,5
5
180

6
3
8
6
4
4,5
280

7
4
10
8
6
4
270

8
Спрос (шт.)
100
200
180
300



9
Объемы производства изделий (шт.)

10
Месяц производства
Месяц потребления
Реальный выпуск изделий (шт)

11
1
2
3
4

12
1












=СУММ(В12:Е12)

13
2












=СУММ(В13:Е13)

14
3












=СУММ(В14:Е14)

15
4












=СУММ(В15:Е15)

16
Спрос (шт.)
=СУММ( В12:В15)
=СУММ( С12:С15)
=СУММ( D12:D15)
=СУММ( Е12:Е15)



17
Суммарные издержки дисбаланса $
=СУММПРОЙЗВ( В12:Е15; В4:Е7)


Функция СУММ() находится в списке функций системы EXCEL.

Она реализует суммирование элементов массива. Функция СУММПРОИЗВ() суммирует произведения элементов двух массивов. Она также находится в списке функций EXCEL. Например,

СУММПРОИЗВ(В12:Е15; В4:Е7) = B12*B4+C12*C4+D12*D4+E12*E4+ B13*B5+C13*C5+D13*D5+E13*E5+ B14*B6+C14*C6+D14*D6+E14*E6+ B15*B7+C15*C7+D15*D7+E15*E7.

Изменяемые ячейки: В12:Е15, целевая ячейка F17. Ограничения:

по производственной программе: F4:F7=F12:F15; по спросу: В8:Е8=В16:Е16; естественные:

В12.Е15 целые, неотрицательные.


Задание 3. Составление «скользящих» графиков

Такие графики обычно связаны с расписаниями многосменной работы предприятия в условиях нестационарного спроса на товары или услуги, связанные с деятельностью этого предприятия. Эти задачи характеризуются наличием многих ограничений, действующих в разные периоды времени. Например, спрос на общественный транспорт сильно меняется в зависимости от времени суток, спрос на продаваемые товары в магазине меняется в зависимости от дня недели и времени суток и т. д. Задача состоит в том, чтобы организовать расписание обслуживания клиентов (пассажиров, покупателей и т. п.) таким образом, чтобы издержки от неравномерности спроса были бы минимальны.

Ниже приводится пример задачи, связанной с неравномерностью покупательского спроса в течение суток.

Составление скользящего расписания при нестационарном потребительском спросе

В таблице приведено количество продавцов, которое необходимо для удовлетворения покупательского спроса в торговом зале магазина в течение суток. Требуется так организовать расписание работы продавцов, чтобы их общее количество (и соответственно расходы на оплату их труда) было минимальным.



Время суток
Требуемое количество продавцов

0-4
2

4-8
2

8-12
5

12-16
7

16-20
7

20-24
4


Математическая формулировка задачи

Допустим, что продавцы в магазине работают по 8 часов (в смену).

В соответствии с данными задачи количество требуемых продавцов меняется через 4 часа. Если предположить, что в первую смену работает X1 продавцов, во вторую — Х2 и т. д., то график работы продавцов можно представить следующим рисунком.




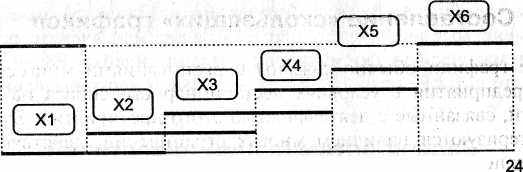
Жирные линии означают смены, которые начинаются через 4 часа и продолжаются 8 часов. Смены перекрываются, т. е., например, с 4 до 8 часов в торговом зале присутствуют (X1 + Х2) продавцов, с 8 до 12 часов — (Х2 + ХЗ) продавцов, а с 0 часов до 4 работают (X1 + Х6) продавцов. Этот «скользящий» график и образует расписание смен.

X1 •*• Х6 определяют изменяемые (варьируемые) переменные, которые следует определять из условия минимального общего количества продавцов, т.е. целевая функция в этой задаче определяется выражением:

(Xl+X2+X3+X4+X5+X6)=>min.

В качестве ограничений при этом будут выступать условия: Х1+Х6>=2; Х1+Х2>=2; Х2+Х3>=5; Х3+Х4>=7; Х4+Х5>=7; Х5+Х6>=4.

Кроме того, (X1 + X6) должны быть целыми и положительными. Такая структуризация может быть реализована, например, в следующей электронной таблице.




1
А
В
С
D
Е
F




Номер смены
Начало смены (час)
Интервал времени (час)
Кол-во продавцов в смене
Кол-во продавцов в зале
Требуемое кол-во продавцов

2
1
0
0-4



=D7+D2
2

3
2
4
4-8



=D2+D3
2

4
3
8
8-12



=D3+D4
5

5
4
12
12-16



=D4+D5
7

6
5
16
16-20



=D5+D6
7

7
6
20
20-24



=D6+D7
4

8
Общее количество продавцов
=СУММ (D2:D7)


Изменяемые ячейки: СЗ:С4, ЕЗ:Е4. В двух первых размещаются вложения первого года, в двух последних — вложения второго года. Ограничения: С5 = Н6; Е5 = D5; Целевая ячейка: Н5.