Geum.ru

Кафедра естественнонаучных и математических дисциплин современные проблемы естественнонаучных и математических дисциплин материалы межкафедрального семинара ббк 20 Рецензенты: Канн К. Б

Вид материалаСеминар

Содержание


Кознов в. в., к. ф.-м. н.
Развитие математических способностей
Подобный материал:
1   ...   7   8   9   10   11   12   13   14   15

Кознов в. в., к. ф.-м. н.

СОФ ГОУВПО «БелГУ»

г. Старый Оскол



Всякая динамическая проблема заключается в определении движения одной или несколько материальных точек, на которые действуют определённые, известные силы. Действующие силы могут быть весьма разнообразны по своей природе и по своему аналитическому строению. В большинстве классических задач небесной механики действующие силы — силы взаимных притяжений по закону Ньютона, зависящие только от взаимных расстояний движущихся тел. В более сложных случаях, например, движение твёрдых тел, движение тел с изменяющейся массой, движение в сопротивляющейся среде, действующие силы могут зависеть также от времени и от скоростей движущихся точек.

Определение движения заключается в определении положения и скоростей движущихся точек для любого момента времени, если известно начальное положение и начальные скорости.

Эта задача сводится к определению координат и компонент скоростей движущихся точек как функций от времени, т. е. к нахождению нескольких неизвестных функций от времени. К сожалению, в громадном большинстве случаев эта задача не разрешима. Действительно, движение всякой динамической системы под действием, известных, заданных сил определяется системой дифференциальных уравнений, от решения которых и зависит возможность найти координаты точек системы как явные функции времени.

Решение всякой системы дифференциальных уравнений такого рода представляет задачу огромной трудности, и может быть проведено только в самых простых случаях, например, задача двух тел, задача двух неподвижных центров, задача о движении точки, масса которой изменяется по закону И. В. Мещерского. Но уже задача трёх тел неразрешима.

Поэтому с давних пор теоретическая наука занималась поиском других методов, достаточных для удовлетворения насущных нужд практики. Так создавалась классическая небесная механика. В основе методов классической небесной механики лежит теория рядов. Теория рядов позволила построить таблицы, при помощи которых можно определить положение любого небесного тела с достаточной для практики точности и для довольно больших промежутков времени. На очереди стали проблемы о совместном изучении поступательного и вращательного движения деформируемых тел, простейшим случаем которых является абсолютно твёрдое тело.

Постановка задачи, вывод дифференциальных уравнений, описывающих совместное поступательно-вращательное движение твёрдых тел, в абсолютной системе были получены в 1958 году независимо друг от друга Г. Н. Дубошиным (Дубошин, 1958) и В. В. Белецким (Белецкий, 1958). Эти работы фактически положили начало активных исследований проблемы поступательно-вращательного движения твёрдых тел в общем, виде. Уравнения, описывающие поступательно-вращательное движение двух твёрдых тел в барицентрической системе, можно записать в векторной форме (Видякин, 1995):

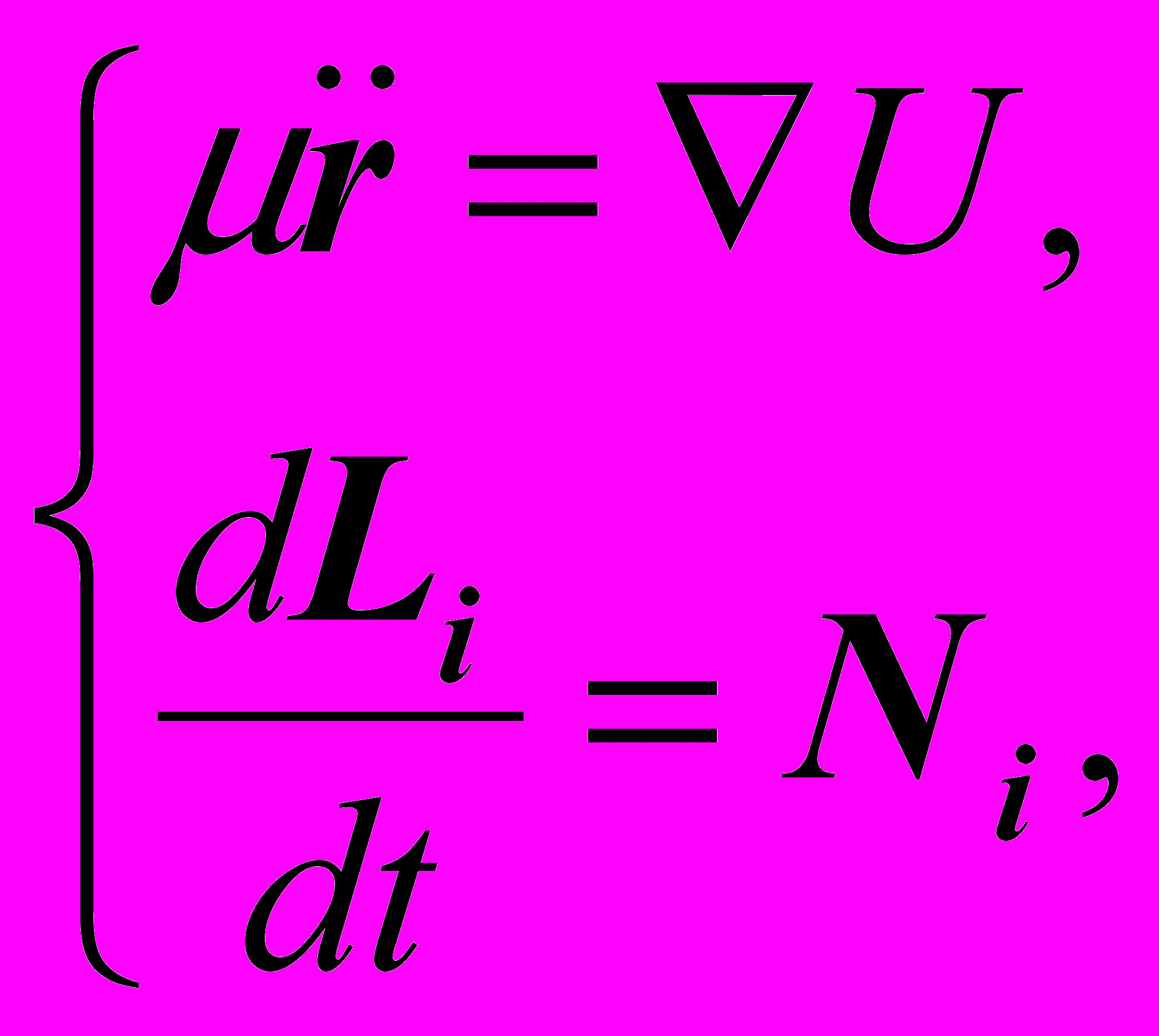(1)

где  — приведённая масса, U — силовая функция взаимного притяжения твёрдых тел, Li — вектор момента импульса, Ni — главный момент всех внешних сил.

Первое уравнение системы (1) описывает поступательное движение центра масс тел системы, второе уравнение — вращательное движение твёрдых тел относительно центра масс.

Так как общее решение системы (1) на данный момент неизвестно, и представляет для исследователей математические трудности, которые непреодолимы и сегодня, то исследователи пошли по пути формирования более частных задач, решения которых можно получить тем или иным способом.

Простейшая из этих задач, движение двух шарообразных тел, которая сводиться к классической задаче о движении двух материальных точечных тел, решённой Ньютоном.

Далее исследователи пытались решать простейшие задачи, связанные с движением однородных сфероидов, эллипсоидов. Но задача оказалась не разрешимой до конца, поэтому был исследован вариант поиска так называемых регулярных движений, которые ввёл в 1961 году Г. Н. Дубошин. Если движение твёрдых тел задано в виде дифференциальных уравнений, общий вид которых можно записать в виде

,

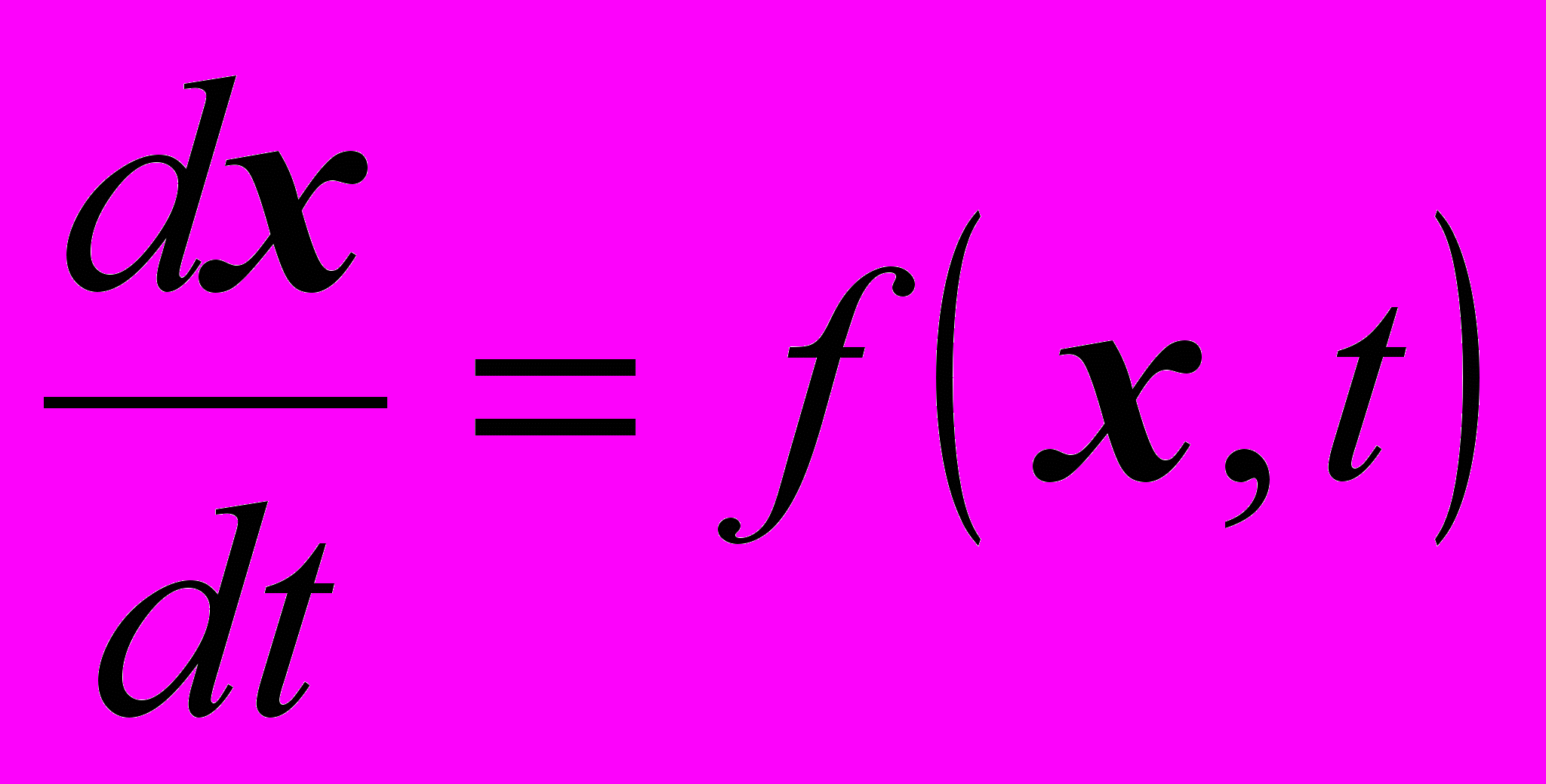то регулярным решением этого дифференциального уравнения называется вектор x=at+ b, где a и b — постоянные вектора.

Для системы уравнений (1) можно описать регулярное движение (Видякин, 1995):

U=const, Ni=const.

Другой вариант, когда U≠const, Ni≠const получил название полурегулярных движений.

Одной из самых знаменитых задач классической и небесной механики является задача о поступательно-вращательном движении трёх твердых тел. Она представляет большие трудности для её полного решения, несмотря на глубокие результаты, полученные крупнейшими математиками последних столетий — Л. Эйлером, Ж. Лагранжем, С. Пуассоном, А. Пуанкаре, А. М. Ляпуновым и др.

Основные результаты были получены в исследовании задачи о поступательном движении трёх материальных точечных тел. Эта задача равносильна задаче о поступательно-вращательном движении трёх твёрдых шаров, однородных или со сферическим распределением плотностей.

Л. Эйлер и Ж. Лагранж заметили, что задача допускает простые частные решения, в которых все три тела находятся в одной неизменной плоскости, и каждое из тел описывает кеплеровскую орбиту с общим фокусом в центре масс системы. Это так называемые точки либрации. При этом конфигурация тел остается неизменной, и три тела во всё время движения либо располагается на одной прямой — коллинеарные или Эйлеровы решения, либо расположены в вершинах равностороннего треугольника — Лагранжевы решения. Как показал К. Астуфман, других решений эта задача не имеет.

Оказалось, что эти решения представляют не только теоретическое, но и практическое значение. Поэтому представляет интерес следующая проблема: выяснить необходимые и достаточные условия существования частных решений неограниченной задачи о поступательно-вращательном движении трёх твердых тел, аналогичных Эйлеровым и Лагранжевым решениям задачи о движении трех точечных тел.

Первые результаты в этом направлении были получены В.В.Видякиным (Видякин, 1982) в задаче о движении трёх однородных сфероидов. По этой проблеме была проделана значительная работа целым рядом исследователей (Дубошин, 1974; Кондурарь, Гамарник, 1980).

Теория поступательно-вращательного движения твёрдых тел находит широкое приложение в космонавтике. Астрономы давно обратили внимание на возможность существования небесных объектов в точках либрации для различных систем типа Солнце — Юпитер, Земля — Луна. Если первые исследования были направлены на поиски объектов только в точках либрации, то последующие проводились в их окрестности с учётом влияния третьих тел. Так было показано, что влияние Солнца на объекты в треугольных точках либрации системы Земля — Луна могут приводить к неограниченным движениям. Вместе с тем было показано, что начальные условия могут быть подобраны таким образом, что частица или другое точечное тело пренебрежительно малой массой будет находиться в окрестности точек либрации достаточно долго. Многие исследователи неоднократно указывали на целесообразность использования либрационных точек системы Земля — Луна в качестве мест дислокации космических аппаратов и ставили вопрос о создании искусственных спутников-либроидов на орбите барицентра Земли и Луны. Поэтому перед исследователями ставится задача создания искусственного тела, которое удовлетворяло бы по своей структуре и форме выдвинутым требованиям так, что заданная точка окажется для него либрационной.


Развитие математических способностей

в процессе преподавания математики