В г. Брянске кафедра гумантарных, естественнонаучных и математических дисциплин бирюлина Е. В. Рабочая программа
| Вид материала | Рабочая программа |
- В г. Брянске кафедра гумантарных, естественнонаучных и математических дисциплин бирюлина Е., 108.51kb.
- В г. Брянске кафедра гумантарных, естественнонаучных и математических дисциплин бирюлина Е., 147.54kb.
- В г. Брянске кафедра гуманитарных, естественнонаучных и математических дисциплин гессе, 102.46kb.
- В г. Брянске кафедра гуманитарных, естественнонаучных и математических дисциплин миронова, 195.11kb.
- В г. Брянске кафедра гуманитарных, естественнонаучных и математических дисциплин миронова, 271.06kb.
- В г. Брянске кафедра гуманитарных, естественнонаучных и математических дисциплин гессе, 68.52kb.
- В г. Брянске кафедра гуманитарных, естественнонаучных и математических дисциплин миронова, 488.05kb.
- В г. Брянске кафедра гуманитарных, естественнонаучных и математических дисциплин миронова, 276.17kb.
- В г. Брянске кафедра гуманитарных, естественнонаучных и математических дисциплин миронова, 286.52kb.
- Факультет экономики и финансов кафедра общих математических и естественнонаучных дисциплин, 212.99kb.
ФИЛИАЛ НОУ ВПО
«МОСКОВСКИЙ ПСИХОЛОГО-СОЦИАЛЬНЫЙ ИНСТИТУТ»
в г. Брянске
КАФЕДРА ГУМАНТАРНЫХ,
ЕСТЕСТВЕННОНАУЧНЫХ И МАТЕМАТИЧЕСКИХ ДИСЦИПЛИН
Бирюлина Е.В.
РАБОЧАЯ ПРОГРАММА
По курсу «Математика»
Специальность 080105.65
«Финансы и кредит»
Рекомендовано Ученым советом БФ МПСИ
(протокол № 1 от 31 августа 2011 г.)
Одобрено кафедрой гуманитарных, естественнонаучных
и математических дисциплин
(протокол № 1 от 26 августа 2011 г.)
БРЯНСК 2011
Пояснительная записка
Предмет «Математика» включён в цикл общих математических и естественнонаучных дисциплин подготовки специалиста по специальности 080105.65 Финансы и кредит и является фундаментальной базой экономического образования.
Цель курса: познакомить студентов с основами современного математического аппарата как средства решения теоретических и практических задач.
Задачи курса:
- раскрыть роль математики в системе научного знания;
- ознакомить студентов с основными математическими структурами и методами;
- обеспечить базовые знания для изучения специальных дисциплин;
- сформировать умения и навыки, необходимые для самостоятельного овладения математической информацией;
- развить логическое и алгоритмическое мышление, умение точно формулировать задачу и использовать полученные знания при изучении других предметов.
Требования к уровню усвоения содержания дисциплины:
в результате изучения курса студент должен
ЗНАТЬ:
- роль математики в системе современного научного знания;
- основные понятия и структуры математики;
- методы и приёмы решения типовых задач;
- основы аналитической геометрии и линейной алгебры;
- элементы математического анализа (дифференциальное и интегральное исчисления, методы решения дифференциальных уравнений);
- базовые основы теории вероятностей и математической статистики;
- математические методы и модели, применяемые в экономике;
УМЕТЬ:
- точно и сжато формулировать математические факты;
- применять основные методы и приёмы решения типовых примеров и задач различной сложности;
- грамотно оценивать и анализировать полученные результаты;
- использовать математический аппарат для решения экономических задач.
Рабочая программа по дисциплине «математика» составлена в соответствии с требованиями государственного стандарта высшего профессионального образования по специальности 080105.65 Финансы и кредит.
Требования государственного образовательного стандарта высшего профессионального образования по дисциплине «математика»
Линейная алгебра с элементами аналитической геометрии: операции над векторами и матрицами; системы линейных алгебраических уравнений; определители и их свойства; собственные значения матриц; комплексные числа; прямые и плоскости в аффинном пространстве; выпуклые множества и их свойства.; математический анализ и дифференциальные уравнения: предел последовательности и его свойства; предел и непрерывность функции; экстремумы функций нескольких переменных; неопределенный и определенный интегралы; числовые и степенные ряды; дифференциальные уравнения первого порядка; линейные дифференциальные уравнения с постоянными коэффициентами. Теория вероятностей и математическая статистика: случайные события; частота и вероятность; основные формулы для вычисления вероятностей; случайные величины; числовые характеристики дискретной и непрерывной случайных величин; нормальный закон распределения; генеральная совокупность и выборка; оценки параметров; корреляция и регрессия. Экономико-математические методы: линейное и целочисленное программирование; графический метод и симплекс-метод решения задач линейного программирования; динамическое программирование; рекуррентные соотношения Беллмана; математическая теория оптимального управления; матричные игры; кооперативные игры; игры с природой; плоские графы; эйлеровы графы; гамильтоновы графы; орграфы; сетевые графики; сети Петри; марковские процессы; задачи анализа замкнутых и разомкнутых систем массового обслуживания. Экономико-математические модели: функции полезности; кривые безразличия; функции спроса; уравнение Слуцкого; кривые “доход-потребление”; кривые “цены-потребление”; коэффициенты эластичности; материальные балансы; функции выпуска продукции; производственные функции затрат ресурсов; модели поведения фирмы в условиях совершенной и несовершенной конкуренции; модели общего экономического равновесия; модель Эрроу-Гурвица; статистическая и динамическая модели межотраслевого баланса; общие модели развития экономики; модель Солоу.
Объём дисциплины и виды учебной работы
| Виды учебной работы | Всего часов в семестр | ||
| I | II | III | |
| Аудиторная | 16 | 16 | 16 |
| Лекции | 10 | 10 | 10 |
| Практическая работа | 6 | 6 | 6 |
| Самостоятельная работа | 188 | 188 | 188 |
| Общее количество часов | 612 | ||
| Вид итогового контроля | зачёт | зачёт | экзамен |
Тематический план курса
| № п/п | Наименование тем | Заочная форма обучения | ||
| Количество часов | ||||
| Лекции | Практическая работа | Самостоятельная работа | ||
| Введение в предмет | ||||
| | Введение в математику | 0 | 0 | 12 |
| | Основные математические предложения | 0 | 0 | 12 |
| Аналитическая геометрия и линейная алгебра | ||||
| | Векторы. Линейные и нелинейные операции над векторами | 0 | 0 | 15 |
| | Матрицы. Операции над матрицами | 2 | 2 | 10 |
| | Определители и их свойства | 10 | ||
| | Обратная матрица | 10 | ||
| | Системы линейных уравнений и методы их решения | 2 | 10 | |
| | Аналитическая геометрия на плоскости и в пространстве | 0 | 0 | 20 |
| | Множества. Основные числовые множества | 2 | | 10 |
| | Комплексные числа | | 10 | |
| Элементы математического анализа | ||||
| | Функции одной переменной | 2 | 2 | 10 |
| | Предел числовой последовательности и его свойства | 10 | ||
| | Предел и непрерывность функции одной переменной | 10 | ||
| | Дифференциальное исчисление функции одной переменной | 2 | 2 | 10 |
| | Приложения производной | 10 | ||
| | Дифференциальное исчисление функции нескольких переменных | 0 | 0 | 19 |
| | Интегральное исчисление функции одной переменной. Неопределённый интеграл | 2 | 2 | 15 |
| | Определённый интеграл. Приложения определённого интеграла | 15 | ||
| | Несобственный интеграл | 0 | 0 | 20 |
| | Дифференциальные уравнения | 2 | 0 | 15 |
| | Ряды | 0 | 0 | 20 |
| Элементы теории вероятностей и математической статистики | ||||
| | Классическое определение вероятности | 2 | 2 | 10 |
| | Формулы комбинаторики | 15 | ||
| | Общие определения вероятности. Условная вероятность | 2 | 15 | |
| | Формула полной вероятности. Формула Байеса | 0 | 10 | |
| | Схема Бернулли. Наивероятнейшее число наступления события | 0 | 10 | |
| | Цепи Маркова | 0 | 0 | 15 |
| | Случайные величины и их числовые характеристики | 0 | 0 | 15 |
| | Основы математической статистики. Корреляция и регрессия | 2 | 2 | 13 |
| Экономико – математические методы и модели | ||||
| | Общая постановка задачи линейного программирования | 2 | 2 | 10 |
| | Геометрический метод решения задачи линейного программирования | 15 | ||
| | Симплексный метод решения задачи линейного программирования | 2 | 15 | |
| | Двойственные задачи | 0 | 0 | 15 |
| | Транспортные задачи | 2 | 2 | 10 |
| | Модели целочисленного линейного программирования | 0 | 0 | 15 |
| | Элементы теории игр | 2 | 2 | 10 |
| | Классические методы оптимизации | 0 | 0 | 15 |
| | Модели выпуклого программирования | 0 | 0 | 15 |
| | Модели динамического программирования | 0 | 0 | 15 |
| | Модели сетевого планирования и управления | 0 | 0 | 15 |
| | Элементы теории массового обслуживания | 0 | 0 | 15 |
| | Обзор других экономико-математических моделей | 2 | 0 | 23 |
| | Аудиторных часов | 30 | 18 | |
| | Общее количество часов | 48 | 564 | |
| | Всего часов | 612 | ||
Содержание курса
Тема 1. Введение в математику.
Математика как наука. Основные этапы становления математики. Структура современной математики.
Тема 2. Основные математические предложения.
Понятия, виды понятий. Определения понятий, способы определения понятий. Теоремы, виды теорем (прямая, обратная, противоположная, противоположная обратной, необходимые и достаточные условия). Способы математических доказательств (дедукция: прямая и косвенная, индукция: полная, неполная, метод математической индукции). Аксиоматический метод построения математической теории.
Тема 3. Векторы. Линейные и нелинейные операции над векторами.
Векторы. Виды векторов. Линейные операции над векторами (сложение, вычитание, умножение вектора на число) и их свойства. Угол между векторами, проекция вектора на ось. Линейно зависимая и линейно независимая системы векторов, базис системы векторов. Координаты вектора. Связь координат вектора с координатами его концов. Координаты суммы, разности векторов и произведения вектора на число. Координаты точки, делящей отрезок в заданном соотношении. Нелинейные операции над векторами (скалярное, векторное, смешанное произведения векторов) и их свойства.
Тема 4. Матрицы. Операции над матрицами.
Матрицы. Виды матриц. Операции над матрицами (сложение, вычитание, умножение матрицы на число, произведение матриц, транспонирование матрицы, возведение матрицы в степень). Элементарные преобразования матриц.
Тема 5. Определители и их свойства.
Определители первого, второго, третьего, n го порядков. Свойства определителей. Минор и алгебраическое дополнение элемента определителя. Разложение определителя n го порядка по строке, разложение определителя n го порядка по столбцу. Векторное и смешанное произведения векторов, заданных своими координатами. Ранг матрицы.
Тема 6. Обратная матрица.
Понятие обратной матрицы. Собственные значения и собственные векторы матриц.
Тема 7. Системы линейных уравнений и методы их решения.
Системы линейных алгебраических уравнений. Основные понятия. Методы решения систем линейных уравнений (метод Гаусса, матричный метод, формулы Крамера).
Тема 8. Аналитическая геометрия на плоскости и в пространстве.
Аффинная система координат на плоскости и в пространстве. Прямая на плоскости, способы задания прямой на плоскости. Расположение прямой относительно системы координат на плоскости. Взаимное расположение двух прямых на плоскости. Геометрический смысл знака трёхчлена
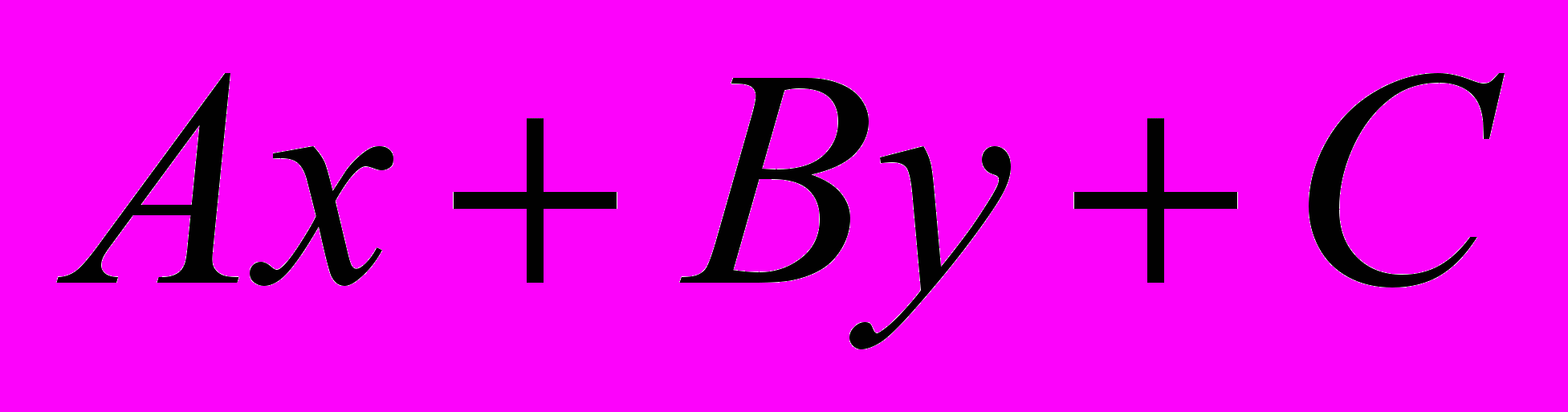. Прямая на плоскости в прямоугольной системе координат. Расстояние от точки до прямой. Угол между прямыми. Плоскость в пространстве, способы задания плоскости в пространстве. Расположение плоскости относительно системы координат. Взаимное расположение двух плоскостей в пространстве. Взаимное расположение трёх плоскостей в пространстве. Плоскость в прямоугольной декартовой системе координат. Прямая в пространстве и способы её задания. Прямая как линия пересечения двух плоскостей.Тема 9. Множества. Основные числовые множества.
Понятие множества. Способы задания множеств, отношения между множествами. Операции над множествами (объединение, пересечение, разность, дополнение множеств), свойства операций над множествами. Мощность множества. Декартово произведение множеств. Основные числовые множества (натуральные, целые, рациональные, иррациональные, действительные числа).
Тема 10. Комплексные числа.
Комплексные числа. Алгебраическая форма записи комплексного числа. Операции над комплексными числами в алгебраической форме. Сопряжённые комплексные числа и их свойства. Модуль комплексного числа и его свойства. Геометрическое изображение комплексных чисел. Тригонометрическая форма записи комплексного числа. Операции над комплексными числами в тригонометрической форме.
Тема 11. Функции одной переменной.
Понятие функции одной переменной. Основные элементарные функции и их графики. Свойства функций (чётность нечётность, монотонность, ограниченность, периодичность). Способы задания функции. Некоторые функции, применяемые в экономике (функции спроса, кривые «доход-потребление», кривые «цены-потребление», функции выпуска продукции, производственные функции затрат ресурсов).
Тема 12. Предел числовой последовательности и его свойства.
Понятие числовой последовательности. Свойства числовых последовательностей (ограниченность, монотонность). Предел числовой последовательности и его свойства. Геометрический смысл предела числовой последовательности. Бесконечно малые, бесконечно большие последовательности и их свойства. Замечательные пределы.
Тема 13. Предел и непрерывность функции одной переменной.
Определение и свойства предела функции в точке и бесконечности. Бесконечно малые величины и их свойства. Бесконечно большие величины и их свойства. Основные теоремы о пределах. Признаки существования предела. Замечательные пределы. Односторонние пределы для функции в точке. Понятие непрерывности функции в точке и на множестве, свойства непрерывных функций. Точки разрыва для функции, классификация точек разрыва.
Тема 14. Дифференциальное исчисление функции одной переменной.
Задачи, приводящие к понятию производной. Понятие производной функции одной переменной. Механический, геометрический и экономический смысл производной. Зависимость между непрерывностью и дифференцируемостью функции. Схема вычисления производной. Основные правила дифференцирования. Производная сложной и обратной функций. Производные основных элементарных функций. Понятие производных высших порядков. Дифференциал функции одной переменной. Свойства дифференциала функции одной переменной. Инвариантность формы дифференциала. Применение дифференциала в приближённых вычислениях. Дифференциалы высших порядков функции одной переменной.
Тема 15. Приложения производной.
Правило Лопиталя. Исследование функции на монотонность и экстремумы. Наибольшее и наименьшее значения функции на отрезке. Выпуклость функции и точки перегиба. Асимптоты графика функции.
Тема 16. Дифференциальное исчисление функции нескольких переменных.
Понятие функции нескольких переменных. Предел и непрерывность функции нескольких переменных. Частные производные функции нескольких переменных. Полный дифференциал функции нескольких переменных. Экстремумы функции нескольких переменных. Применение частных производных в экономике: функции полезности; кривые безразличия производства.
Тема 17. Интегральное исчисление функции одной переменной. Неопределённый интеграл.
Понятие первообразной функции одной переменной. Первообразные основных элементарных функций. Определение и свойства неопределённого интеграла. Некоторые методы вычисления неопределённых интегралов (метод замены переменной, формула интегрирования по частям). Интегрирование рациональных дробей, иррациональностей, тригонометрических выражений.
Тема 18. Определённый интеграл. Приложения определённого интеграла.
Определение и свойства определённого интеграла. Вычисление определённого интеграла, формула Ньютона-Лейбница. Замена переменной и формула интегрирования по частям в определённом интеграле. Экономический смысл интеграла. Использование понятия определённого интеграла в экономике. Геометрические приложения определённого интеграла (вычисление площади плоской фигуры, длины дуги, объёма тела вращения, площади поверхности вращения).
Тема 19. Несобственный интеграл.
Определение и свойства несобственного интеграла. Вычисление несобственного интеграла.
Тема 20. Дифференциальные уравнения.
Дифференциальные уравнения первого порядка. Постановка задачи и основные теоремы. Общее и частное решение. Интегрирование некоторых классов уравнений первого порядка (с разделяющимися переменными, однородные уравнения, дифференциальные уравнения, сводящиеся к однородным, дифференциальные уравнения в полных дифференциалах, линейные дифференциальные уравнения первого порядка, уравнения Бернулли). Дифференциальные уравнения высших порядков: линейные однородные уравнения, линейные однородные уравнения с постоянными коэффициентами, линейные неоднородные уравнения.
Тема 21. Ряды.
Определение и свойства числовых рядов. Понятие сходимости числовых рядов. Признаки сравнения и признаки сходимости числовых рядов. Функциональные ряды. Область сходимости функционального ряда, признаки сходимости. Степенные ряды. Радиус и интервал сходимости степенного ряда.
Тема 22. Классическое определение вероятности.
Основные понятия теории вероятностей (событие, виды событий, действия над событиями, вероятность события, пространство элементарных событий). Классическое определение вероятности. Свойства вероятности. Относительная частота, статистическое определение вероятности. Геометрическое определение вероятности.
Тема 23. Формулы комбинаторики.
Комбинаторика как раздел математики. Правила суммы и произведения. Размещения с повторениями и без повторений. Сочетания без повторений, свойства сочетаний. Размещения заданного состава, полиномиальная формула. Применение формул комбинаторики к решению задач по теории вероятностей.
Тема 24. Общие определения вероятности. Условная вероятность.
Понятие алгебры событий. Аксиомы, задающие вероятность. Теорема о вероятности суммы двух событий. Зависимые события. Условная вероятность. Независимые события, нахождение вероятности произведения независимых событий.
Тема 25. Формула полной вероятности. Формула Байеса.
Понятие полной группы событий. Формула полной вероятности. Формула Байеса.
Тема 26. Схема Бернулли. Наивероятнейшее число наступления события.
Схема Бернулли. Наиболее вероятное число успехов. Среднее число успехов.
Тема 27. Цепи Маркова.
Определение и способ задания цепи Маркова. Примеры Марковских цепей. Нахождение вероятностей переходов за несколько шагов. Предельные вероятности.
Тема 28. Случайные величины и их числовые характеристики.
Определение и виды случайных величин. Числовые характеристики дискретных случайных величин. Примеры распределения дискретных случайных величин. Непрерывные случайные величины. Функции распределения непрерывных случайных величин. Числовые характеристики непрерывных случайных величин. Понятие нормально распределённой величины. Нормированные случайные величины.
Тема 29. Основы математической статистики. Корреляция и регрессия.
Понятия генеральной совокупности и выборки. Определение характеристик случайных величин на основе опытных данных. Корреляция и регрессия.
Тема 30. Общая постановка задачи линейного программирования.
Экономико-математическая модель. Примеры задач линейного программирования. Общая постановка задачи линейного программирования.
Тема 31. Геометрический метод решения задачи линейного программирования.
Выпуклые множества и их свойства. Геометрический смысл решений неравенств, уравнений и их систем. Геометрический метод решения задачи линейного программирования.
Тема 32. Симплексный метод решения задачи линейного программирования.
Геометрическая интерпретация задачи линейного программирования. Отыскание максимума и минимума линейной функции. Определение допустимого базисного решения. Особые случаи симплексного метода. Симплексные таблицы. Симплекс-метод решения задачи линейного программирования.
Тема 33. Двойственные задачи.
Взаимно двойственные задачи и их свойства. Теоремы двойственности. Объективно обусловленные оценки и их смысл.
Тема 34. Транспортные задачи.
Экономико-математическая модель транспортной задачи. Нахождение первоначального базисного распределения поставок. Критерий оптимальности базисного распределения поставок. Распределительный метод решения транспортной задачи.
Тема 35. Модели целочисленного линейного программирования.
Постановка задачи целочисленного программирования. Методы отсечения. Метод Гомори. Понятие о методе ветвей и границ.
Тема 36. Элементы теории игр.
Предмет теории игры. Терминология и классификация игр. Матричные игры, приведение матричной игры к задаче линейного программирования. Кооперативные игры. Игры с природой.
Тема 37. Классические методы оптимизации.
Классические методы определения экстремумов. Метод множителей Лагранжа.
Тема 38. Модели выпуклого программирования.
Задача выпуклого программирования. Приближённое решение задач выпуклого программирования методом кусочно-линейной аппроксимации. Методы спуска. Приближённое решение задач выпуклого программирования градиентным методом.
Тема 39. Модели динамического программирования.
Общая постановка задачи динамического программирования. Принцип оптимальности и уравнения Беллмана. Задача о распределении средств между предприятиями. Общая схема применения метода динамического программирования. Задача об оптимальном распределении ресурсов между отраслями на
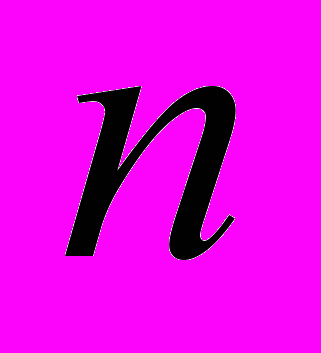лет. Задача о замене оборудования.Тема 40. Модели сетевого планирования и управления.
Понятие графа. Плоские графы. Эйлеровы графы. Гамильтоновы графы. Модели сетевого планирования и управления: назначение и область применения, сетевая модель и её основные элементы, порядок и правила построения сетевых графиков, оптимизация сетевого графика.
Тема 41. Элементы теории массового обслуживания.
Основные понятия, классификация, марковские процессы, потоки событий. Задачи анализа замкнутых и разомкнутых систем массового обслуживания.
Тема 42. Обзор других экономико-математических моделей.
Модели поведения фирмы в условиях совершенной и несовершенной конкуренции, модели общего экономического равновесия, модель Эрроу-Гурвица, статическая и динамическая модели межотраслевого баланса, общие модели развития экономики, модель Солоу.