Geum.ru

В г. Брянске кафедра гумантарных, естественнонаучных и математических дисциплин бирюлина Е. В. Рабочая программа

Вид материалаРабочая программа
Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем: Учебное пособие. – М.: Финансы и статисти
Подобный материал:
1   2   3

Литература


Основная

  1. Баврин И.Н., Матросов В.Л. Общий курс высшей математики: Учеб. для студентов физ.-мат. спец. пед. вузов. – Москва: Просвещение, 1995. – 464 с.1
  2. Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем: Учебное пособие. – М.: Финансы и статистика, 2001. – 368 с.
  3. Высшая математика для экономистов: Учебник для вузов: Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н.; Под ред. проф. Н.Ш. Кремера. – 2-е изд., перераб. и доп. – М.: Банки и биржи, ЮНИТИ, 1998. – 471 с.2
  4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х частях. Часть I: Учеб. пособие для вузов. – 6-е издание. – М.: Оникс, 2006. – 304 с.
  5. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х частях. Часть II: Учеб. пособие для вузов. – 6-е издание. – М.: Мир и Образование, 2006. – 416 с.
  6. Исследование операций в экономике: Учебное пособие для вузов / Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н.; Под ред. проф. Н.Ш. Кремера.– М.: ЮНИТИ, 2004. – 407 с.
  7. Малыхин В.И. Математика в экономике: Учебное пособие. – М.: ИНФРА-М, 2000. – 356 с.
  8. Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред. В.И. Ермакова. – М.: ИНФРА М, 2001.   575 с.
  9. Солодовников А.С. Теория вероятностей: Учебное пособие для студентов пед. ин-тов по математическим специальностям. – М.: Просвещение, 1983. – 207 с.
  10. Шелобаев С.И. Математические методы и модели в экономике, финансах, бизнесе: Учеб. пособие для вузов. – М.: ЮНИТИ-ДАНА, 2001. – 367 с.
  11. Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учебное пособие. – 2-е изд., испр. – М.: Дело, 2002. – 440 с.
  12. Экономико – математические методы и прикладные модели: Учебное пособие для вузов / В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др.; Под ред. В.В. Федосеева. – М.: ЮНИТИ, 2002. – 391 с.


Дополнительная

  1. Аматова Г.М., Аматов М.А. Математика: Учебное пособие. – М.: МПСИ, 1999. – 488 с.
  2. Балдин К.В. Математические методы в экономике. Теория, примеры, варианты контрольных работ: Учебное пособие. – М.: МПСИ; Воронеж: НПО «МОДЭК», 2003. – 112 с.
  3. Беклемишева Л.А., Петрович А.Ю., Чубаров И.А. Сборник задач по аналитической геометрии и линейной алгебре: Учебное пособие / Под ред. Д.В. Беклемишева. – М.: Наука, 1987. – 496 с.
  4. Бородин А.Н. Элементарный курс теории вероятностей и математической статистики. 3 е изд., испр. и доп. – СПб: Издательство «Лань», 2002. – 256 с.
  5. Бухштаб А.А. Теория чисел. – М.: Просвещение, 1966. – 384 с.
  6. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – 7 е изд., доп. – М.: Высшая школа, 2003. – 405 с.
  7. Демидович Б.П. Сборник задач по математическому анализу: Учебное пособие для вузов. – М.: Изд во Астрель. – 2002. – 558 с.
  8. Колесников А.Н. Краткий курс математики для экономистов: Учебное пособие. – М.: ИНФРА-М, 2003. – 208 с.
  9. Конюховский П.В. Математические методы исследования операций в экономике. – СПб: Питер, 2000. – 208 с.
  10. Кремер Н.Ш. Теория вероятностей и математическая статистика. – М.: ЮНИТИ, 2000.
  11. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1986.
  12. Кудрявцев Л.Д. Курс математического анализа: Учебное пособие для студентов университетов и вузов.   2 е изд., перераб. и доп. – В 3 т. – М.: Высшая школа, 1988.
  13. Куликов Ю.Г., Шеховцова Н.Ф., Зикеева Л.П. Экономико – математические методы и модели (раздел «Линейное программирование»): Учебное пособие для практических занятий. – М.: МПСИ; Воронеж: НПО «МОДЭК», 2000. – 96 с.
  14. Лекции по высшей математике. Часть I / Рудаков И.А., Путилов С.В., Лукавый А.П. – Брянск: Издательство БГУ, 2002. – 100 с.
  15. Лекции по высшей математике. Часть II // Рудаков И.А. – Брянск: Издательство БГУ, 2002. – 110 с.
  16. Математическое моделирование экономических систем / А. Лукавый. – Брянск: Изд-во БГУ, 2001. – 52 с.
  17. Пуличева Е.А. Введение в математический анализ. Предел и непрерывность: Пособие для студентов физико – математических факультетов педагогических вузов. – Брянск: Изд во БГПУ, 1998. – 67 с.
  18. Трояновский В.М. Математическое моделирование в менеджменте: Учебное пособие.   2 е изд., испр. и доп. – М.: РДЛ, 2000. – 256 с.
  19. Шнеперман Л.Б. Сборник задач по алгебре и теории чисел. – Мн.: Высшая школа, 1982. – 223 с.


Планы практических занятий

Практическое занятие № 1

Тема: Матрицы. Операции над матрицами. Определители. Обратная матрица. Системы линейных уравнений и методы их решения.

План
  1. Операции над матрицами (сложение, вычитание, умножение матрицы на число, произведение матриц, транспонирование матрицы, возведение матрицы в степень).
  2. Вычисление определителей первого, второго, третьего, четвёртого порядков.
  3. Нахождение обратной матрицы.
  4. Определение ранга матрицы.
  5. Решение систем линейных алгебраических уравнений

Задания: [4. С. 70-78, 86-94], [8. С. 43-49, 50-69].

Практическое занятие № 2

Тема: Функции одной переменной. Предел числовой последовательности и его свойства. Предел и непрерывность функции одной переменной.

План
  1. Нахождение области определения функции одной переменной.
  2. Исследование функции на чётность – нечётность.
  3. Нахождение предела числовой последовательности.
  4. Нахождение предела функции в точке и бесконечности.
  5. Вычисление односторонних пределов функции в точке.
  6. Непрерывность функции в точке.

Задания: [4. С. 137-150], [8. С. 135-148].

Практическое занятие № 3

Тема: Дифференциальное исчисление функции одной переменной. Приложения производной.

План
  1. Вычисление производной функции одной переменной.
  2. Нахождение производных высших порядков функции одной переменной.
  3. Дифференциал функции одной переменной.
  4. Решение задач с использованием механического, геометрического и экономического смыслов производной.
  5. Применение правила Лопиталя для нахождения пределов функции.
  6. Исследование функции.

Задания: [4. С. 151-183], [8. С. 149-154, 159-179].

Практическое занятие № 4

Тема: Интегральное исчисление функции одной переменной. Неопределённый интеграл. Определённый интеграл. Приложения определённого интеграла.

План
  1. Вычисление неопределённых интегралов от функции одной переменной (по таблице интегралов, методом замены переменной, при помощи формулы интегрирования по частям).
  2. Вычисление определённого интеграла функции одной переменной, формула Ньютона-Лейбница.
  3. Замена переменной и формула интегрирования по частям в определённом интеграле.
  4. Геометрические приложения определённого интеграла (вычисление площади плоской фигуры, длины дуги, объёма тела вращения, площади поверхности вращения).

Задания: [4. С. 208-247, 251-258], [8. С. 202-217].

Практическое занятие № 5

Тема: Элементы теории вероятностей. Формулы комбинаторики. Общие определения вероятности. Условная вероятность.

План
  1. Решение задач с применением классического определения вероятности. Относительная частота, статистическое определение вероятности. Геометрическое определение вероятности.
  2. Размещения с повторениями и без повторений. Сочетания без повторений. Применение формул комбинаторики к решению задач по теории вероятностей.
  3. Применение аксиом и теорем вероятности к решению задач.
  4. Вероятность появления хотя бы одного события.
  5. Условная вероятность. Зависимые и независимые события.

Задания: [5. С. 176-183], [8. С. 303-310], [9. С. 32-46], [13. С. 113-114, 119-120].

Практическое занятие № 6

Тема: Основы математической статистики. Корреляция и регрессия.

План
  1. Определение характеристик случайных величин на основе опытных данных.
  2. Корреляция и регрессия.

Задания: [5. С. 223-249], [8. С. 347-360, 388-395].

Практическое занятие № 7

Тема: Геометрический метод решения задачи линейного программирования. Симплексный метод решения задачи линейного программирования.

План
  1. Решение задач линейного программирования геометрическим методом.
  2. Симплекс-метод решения задачи линейного программирования.
  3. Особые случаи симплексного метода.

Задания: [4. С. 271-287], [8. С. 412-456].

Практическое занятие № 8

Тема: Транспортные задачи.

План
  1. Нахождение опорных решений транспортной задачи.
  2. Метод потенциалов решения транспортной задачи.
  3. Транспортная задача с ограничениями на пропускную способность.
  4. Транспортная задача по критерию времени.

Задания: [4. С. 290-293], [8. С. 476-499].

Практическое занятие № 9

Тема: Элементы теории игр.

План
  1. Матричные игры, приведение матричной игры к задаче линейного программирования.
  2. Кооперативные игры.
  3. Игры с природой.

Задания: [6. С. 197-198].


Примерные вопросы к первому зачету

  1. Математика как наука. Основные этапы становления математики. Структура современной математики.
  2. Понятия, виды понятий. Определения понятий, способы определения понятий.
  3. Теоремы, виды теорем. Способы математических доказательств.
  4. Аксиоматический метод построения математической теории.
  5. Векторы. Виды векторов. Линейные операции над векторами.
  6. Угол между векторами. Ортогональная проекция вектора на ось. Теорема о вычислении ортогональной проекции вектора на ось.
  7. Понятия линейной зависимости и линейной независимости векторов. Линейная зависимость векторов на плоскости и в пространстве.
  8. Базис системы векторов. Прямоугольная декартова система координат.
  9. Координаты вектора. Связь координат вектора и координат его концов. Координаты суммы, разности векторов и произведения вектора на число. Координаты точки, делящей отрезок в данном соотношении.
  10. Необходимое и достаточное условие коллинеарности векторов.
  11. Скалярное произведение векторов (определение, свойства). Необходимое и достаточное условие ортогональности векторов. Скалярное произведение векторов, заданных своими координатами.
  12. Векторное произведение векторов (определение, геометрический смысл, свойства). Необходимое и достаточное условие коллинеарности векторов. Векторное произведение векторов, заданных своими координатами.
  13. Смешанное произведение векторов (определение, геометрический смысл). Смешанное произведение векторов, заданных своими координатами.
  14. Матрицы. Виды матриц. Действия над матрицами.
  15. Определители. Свойства определителей.
  16. Обратная матрица (определение, вычисление).
  17. Ранг матрицы.
  18. Системы линейных алгебраических уравнений. Совместные системы (определённые и неопределённые) и несовместные системы. Понятие равносильности систем линейных уравнений.
  19. Системы линейных алгебраических уравнений. Метод Гаусса решения систем линейных уравнений.
  20. Системы линейных алгебраических уравнений. Матричный метод решения систем линейных уравнений. Формулы Крамера.
  21. Аффинная система координат на плоскости и в пространстве.
  22. Прямая на плоскости. Способы задания прямой на плоскости.
  23. Расположение прямой относительно системы координат на плоскости. Взаимное расположение двух прямых на плоскости.
  24. Геометрический смысл знака трёхчлена .
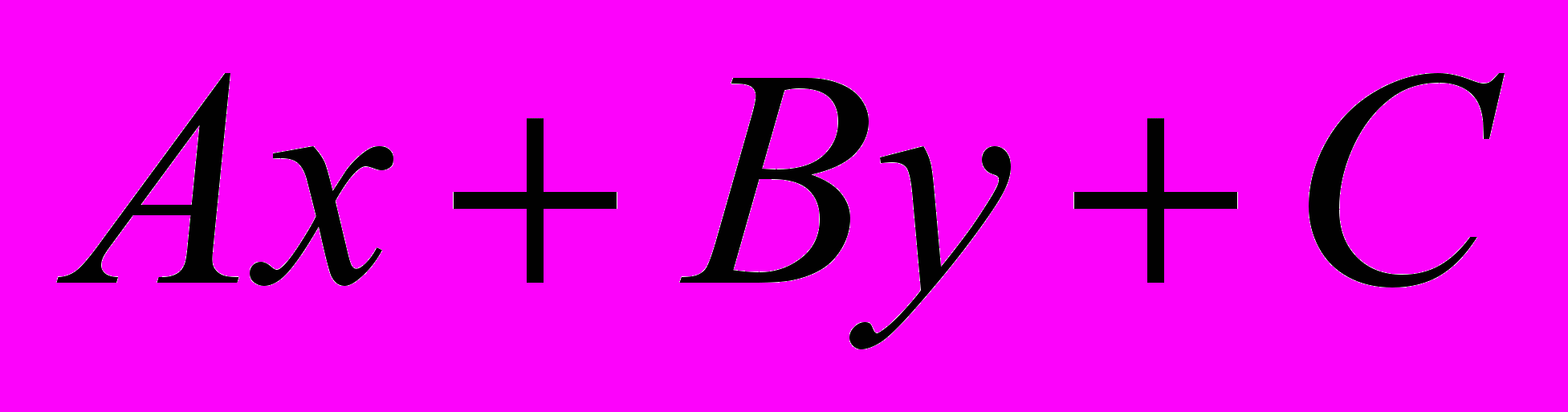  25. Прямая на плоскости в прямоугольной системе координат. Уравнение прямой по точке и нормальному вектору.
  26. Геометрический смысл углового коэффициента прямой. Расстояние от точки до прямой. Угол между прямыми.
  27. Плоскость в пространстве. Способы задания плоскости в пространстве.
  28. Расположение плоскости относительно системы координат. Взаимное расположение двух плоскостей в пространстве.
  29. Взаимное расположение трёх плоскостей в пространстве.
  30. Признак параллельности вектора и плоскости.
  31. Плоскость в прямоугольной декартовой системе координат (уравнение по точке и нормальному вектору, угол между плоскостями, расстояние от точки до плоскости).
  32. Прямая в пространстве и способы её задания. Прямая как линия пересечения двух плоскостей.
  33. Понятие множества. Способы задания множеств, отношения между множествами. Основные числовые множества.
  34. Операции над множествами, свойства операций над множествами.
  35. Декартово произведение множеств.
  36. Комплексные числа. Алгебраическая форма комплексного числа. Операции над комплексными числами в алгебраической форме.
  37. Сопряжённые комплексные числа и их свойства.
  38. Модуль комплексного числа и его свойства.
  39. Комплексные числа. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа.
  40. Операции над комплексными числами в тригонометрической форме.
  41. Понятие функции одной переменной. Основные элементарные функции.
  42. Свойства функции одной переменной.
  43. Основные функции, применяемые в экономике.
  44. Бесконечная числовая последовательность (определение, свойства).
  45. Предел числовой последовательности.
  46. Геометрический смысл предела числовой последовательности. Теоремы о пределах.
  47. Предел функции в точке и в бесконечности.
  48. Бесконечно малые величины и их свойства.
  49. Бесконечно большие величины и их свойства.
  50. Основные теоремы о пределах функций.
  51. Односторонние пределы для функции в точке.
  52. Понятие непрерывности функции в точке и на множестве, свойства непрерывных функций.
  53. Точки разрыва для функции, классификация точек разрыва.
  54. Задачи, приводящие к понятию производной.
  55. Понятие производной функции одной переменной. Механический, геометрический и экономический смысл производной. Зависимость между непрерывностью и дифференцируемостью функции.
  56. Схема вычисления производной. Основные правила дифференцирования.
  57. Производные основных элементарных функций. Понятие производных высших порядков.
  58. Правило Лопиталя.
  59. Исследование функции на монотонность и экстремумы. Наибольшее и наименьшее значения функции на отрезке.
  60. Выпуклость функции. Точки перегиба.
  61. Асимптоты графика функции.
  62. Дифференциал функции одной переменной (определение, геометрический смысл).
  63. Свойства дифференциала функции одной переменной. Инвариантность формы дифференциала.
  64. Применение дифференциала в приближённых вычислениях.
  65. Дифференциалы высших порядков функции одной переменной.
  66. Понятие функции нескольких переменных. Предел и непрерывность функции нескольких переменных.
  67. Частные производные функции нескольких переменных.
  68. Полный дифференциал функции нескольких переменных.
  69. Экстремумы функции нескольких переменных.
  70. Применение частных производных в экономике.


Примерные вопросы ко второму зачету

  1. Понятие первообразной функции одной переменой. Первообразные основных элементарных функций.
  2. Неопределённый интеграл (определение, свойства).
  3. Вычисление неопределённых интегралов методом замены переменной.
  4. Вычисление неопределённых интегралов методом интегрирования по частям.
  5. Интегрирование рациональных дробей.
  6. Интегрирование иррациональностей.
  7. Интегрирование тригонометрических выражений.
  8. Определение и свойства определённого интеграла. Вычисление определённого интеграла, формула Ньютона-Лейбница.
  9. Замена переменной в определённом интеграле.
  10. Формула интегрирования по частям в определённом интеграле.
  11. Экономический смысл интеграла. Использование понятия определённого интеграла в экономике.
  12. Геометрические приложения определённого интеграла (вычисление площади плоской фигуры, длины дуги, объёма тела вращения, площади поверхности вращения).
  13. Определение и свойства несобственного интеграла. Вычисление несобственного интеграла.
  14. Дифференциальные уравнения первого порядка. Постановка задачи и основные теоремы.
  15. Дифференциальные уравнения первого порядка. Общее и частное решение.
  16. Интегрирование некоторых классов дифференциальных уравнений первого порядка (с разделяющимися переменными, однородные уравнения, дифференциальные уравнения, сводящиеся к однородным).
  17. Дифференциальные уравнения в полных дифференциалах, линейные дифференциальные уравнения первого порядка, уравнения Бернулли.
  18. Линейные дифференциальные уравнения с постоянными коэффициентами.
  19. Определение и свойства числовых рядов. Понятие сходимости числовых рядов.
  20. Признаки сравнения и признаки сходимости числовых рядов.
  21. Функциональные ряды. Область сходимости функционального ряда, признаки сходимости.
  22. Степенные ряды. Радиус и интервал сходимости степенного ряда.
  23. Основные понятия теории вероятностей (случайные события, их виды, операции над случайными событиями).
  24. Классическое определение вероятности, свойства вероятности.
  25. Относительная частота. Статистическое определение вероятности.
  26. Геометрическое определение вероятности.
  27. Комбинаторика как раздел математики. Правила суммы и произведения.
  28. Размещения с повторениями и без повторений.
  29. Сочетания без повторений, свойства сочетаний.
  30. Размещения заданного состава, полиномиальная формула.
  31. Общее определение вероятности. Аксиомы А.Н. Колмогорова. Теорема о вероятности суммы событий.
  32. Условная вероятность. Зависимые и независимые события.
  33. Формула полной вероятности. Формула Байеса.
  34. Схема Бернулли. Наивероятнейшее число наступления события.
  35. Определение и способ задания цепи Маркова.
  36. Примеры Марковских цепей.
  37. Марковские цепи. Нахождение вероятностей переходов за несколько шагов. Предельные вероятности.
  38. Определение и виды случайных величин.
  39. Числовые характеристики дискретных случайных величин.
  40. Примеры распределения дискретных случайных величин.
  41. Непрерывные случайные величины. Функции распределения непрерывных случайных величин.
  42. Числовые характеристики непрерывных случайных величин.
  43. Понятие нормально распределённой величины. Нормированные случайные величины.
  44. Определение характеристик случайных величин на основе опытных данных.
  45. Корреляция и регрессия.


Примерные вопросы к экзамену

  1. Математика как наука. Основные этапы становления математики. Структура современной математики.
  2. Виды математических предложений.
  3. Векторы. Виды векторов. Линейные операции над векторами.
  4. Понятия линейной зависимости и линейной независимости векторов. Линейная зависимость векторов на плоскости и в пространстве. Базис системы векторов.
  5. Координаты вектора. Связь координат вектора и координат его концов. Координаты суммы, разности векторов и произведения вектора на число. Координаты точки, делящей отрезок в данном соотношении.
  6. Необходимое и достаточное условие коллинеарности векторов.
  7. Скалярное произведение векторов (определение, свойства). Необходимое и достаточное условие ортогональности векторов. Скалярное произведение векторов, заданных своими координатами.
  8. Векторное произведение векторов (определение, геометрический смысл, свойства). Необходимое и достаточное условие коллинеарности векторов. Векторное произведение векторов, заданных своими координатами.
  9. Смешанное произведение векторов (определение, геометрический смысл). Смешанное произведение векторов, заданных своими координатами.