Кафедра естественнонаучных и математических дисциплин современные проблемы естественнонаучных и математических дисциплин материалы межкафедрального семинара ббк 20 Рецензенты: Канн К. Б

Вид материала

Семинар

Подобный материал:

• Факультет экономики и финансов кафедра общих математических и естественнонаучных дисциплин, 212.99kb.
• Факультет экономики и финансов кафедра общих математических и естественнонаучных дисциплин, 212.78kb.
• В г. Брянске кафедра гумантарных, естественнонаучных и математических дисциплин бирюлина Е., 406.42kb.
• В г. Брянске кафедра гумантарных, естественнонаучных и математических дисциплин бирюлина Е., 108.51kb.
• Факультет экономики и финансов кафедра общих математических и естественнонаучных дисциплин, 90.82kb.
• В г. Брянске кафедра гумантарных, естественнонаучных и математических дисциплин бирюлина Е., 147.54kb.
• В г. Брянске кафедра гуманитарных, естественнонаучных и математических дисциплин миронова, 195.11kb.
• В г. Брянске кафедра гуманитарных, естественнонаучных и математических дисциплин миронова, 271.06kb.
• Развития и торговли, 112.91kb.
• В г. Брянске кафедра гуманитарных, естественнонаучных и математических дисциплин гессе, 68.52kb.

Решение: 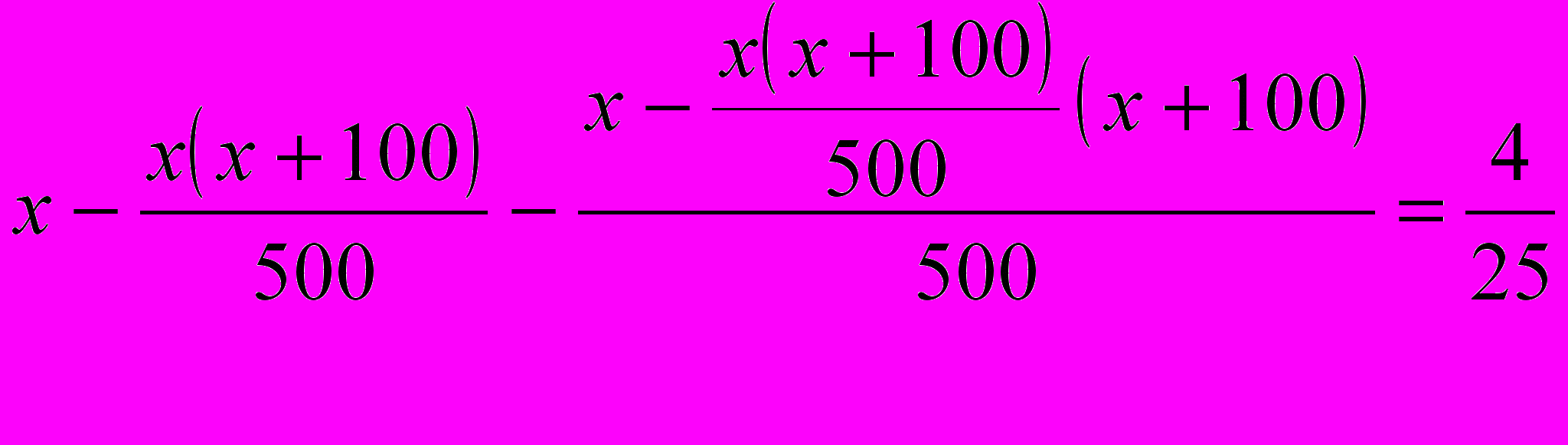х х₁ = 200, х₂=600 600 кг не подходит по смыслу, меди 200 кг, олова 300 кг., .

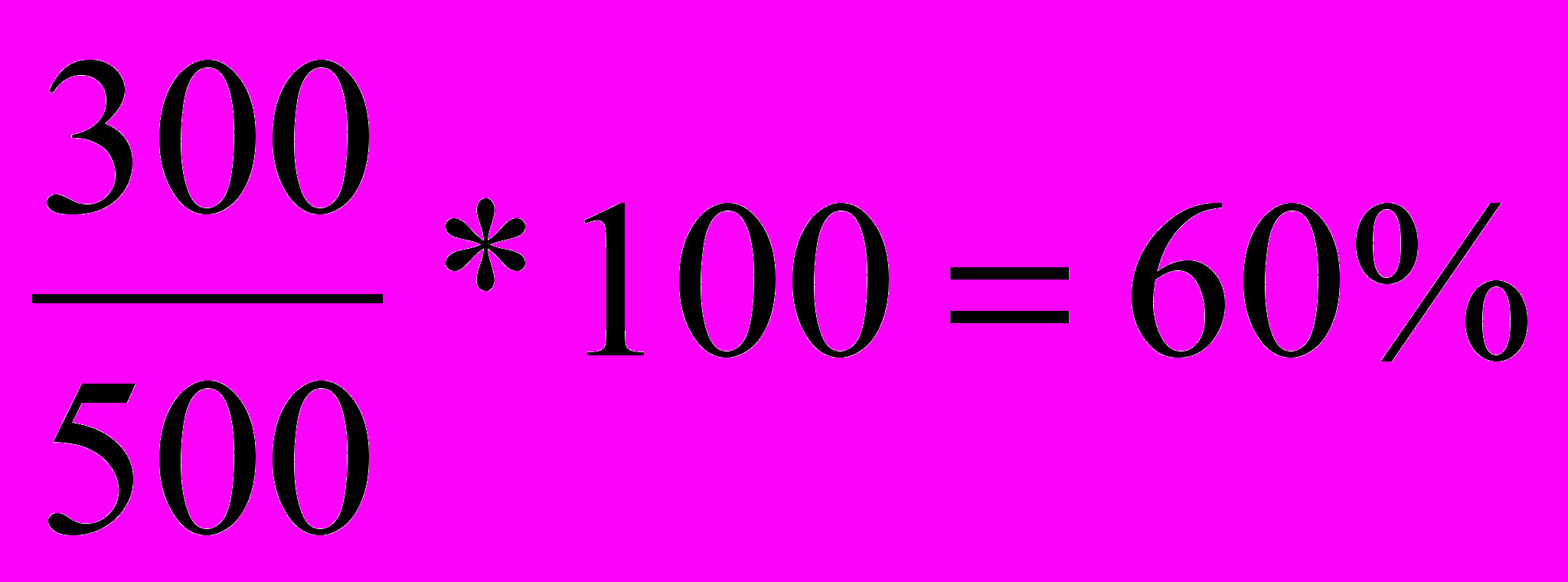Ответ: 60%.

2. Имеются два раствора поваренной соли разной концентрации. Если слить вместе 100 г первого раствора и 200 г второго раствора, то получится 50%-й раствор. Если же слить 300 г первого раствора и 200 г второго, то получится 42%-й раствор. Найти концентрации данных растворов.

	Соль (г)	Общее кол-во (г)
1 раствор	х	100
2 раствор	150-х	200
1 + 2 раствор	0,5*300=150 г.	300
1 раствор		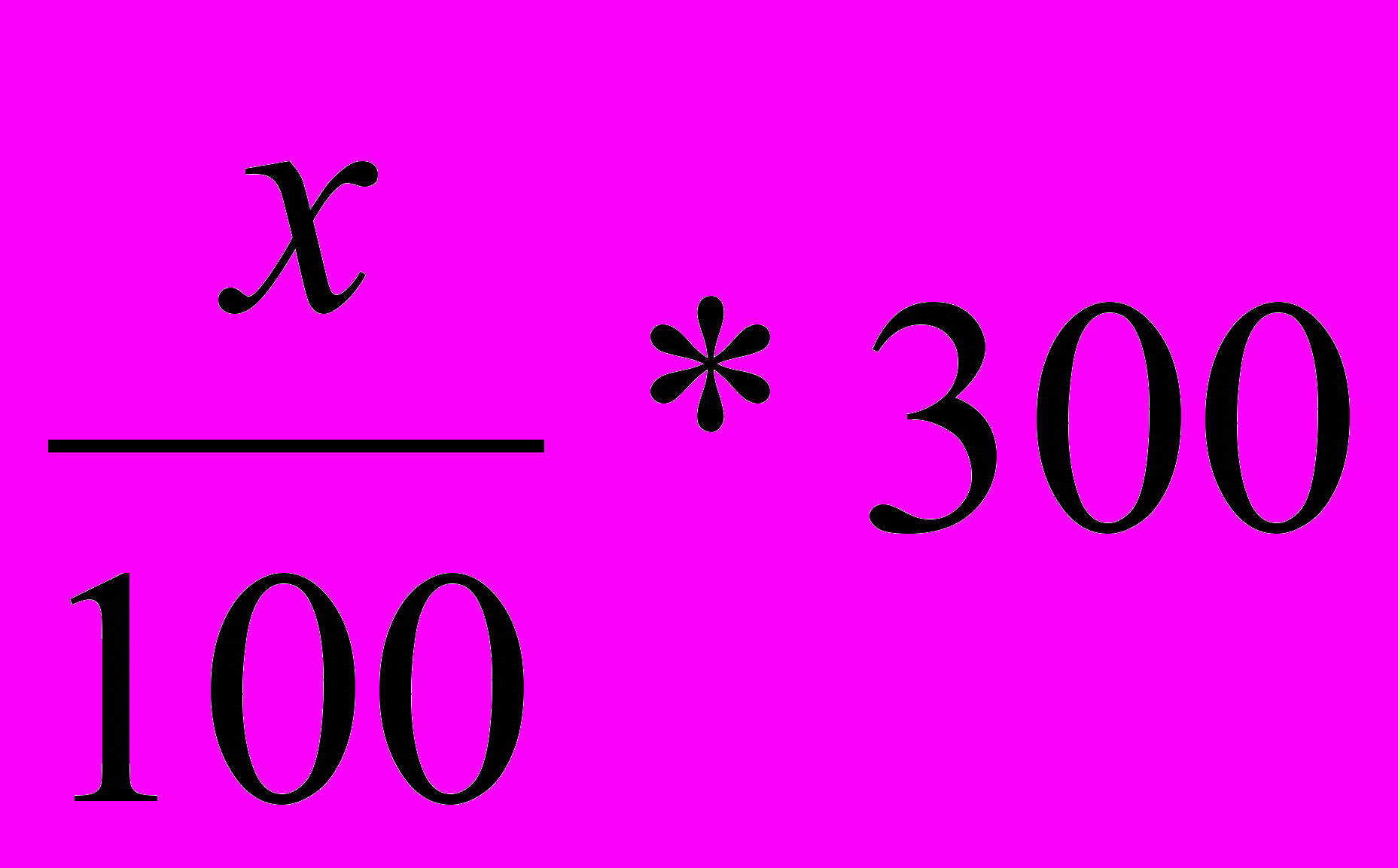300
2 раствор		200
1+2 раствор	0,42*500=210	500

Решение:1) 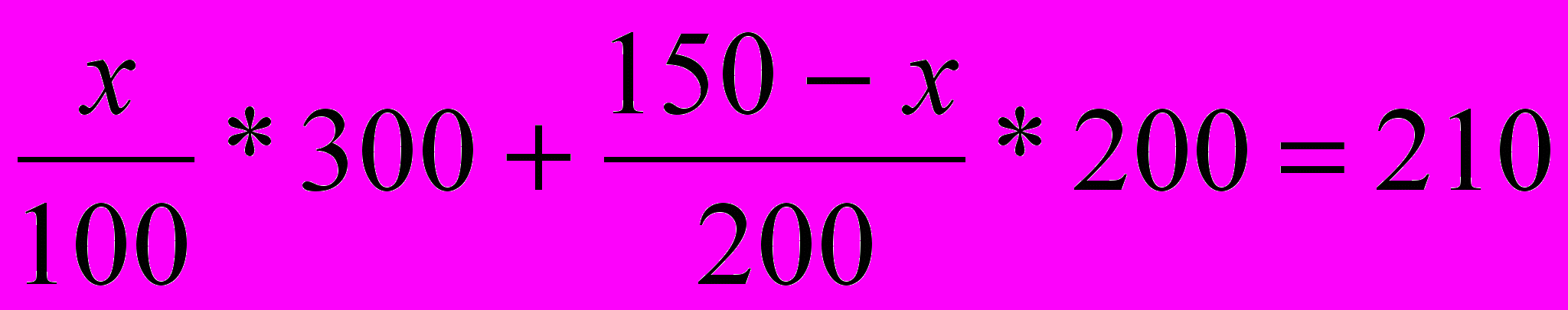,х=30,30 г соли или 30% в1раств.,

2) 150-30 = 120 (г), 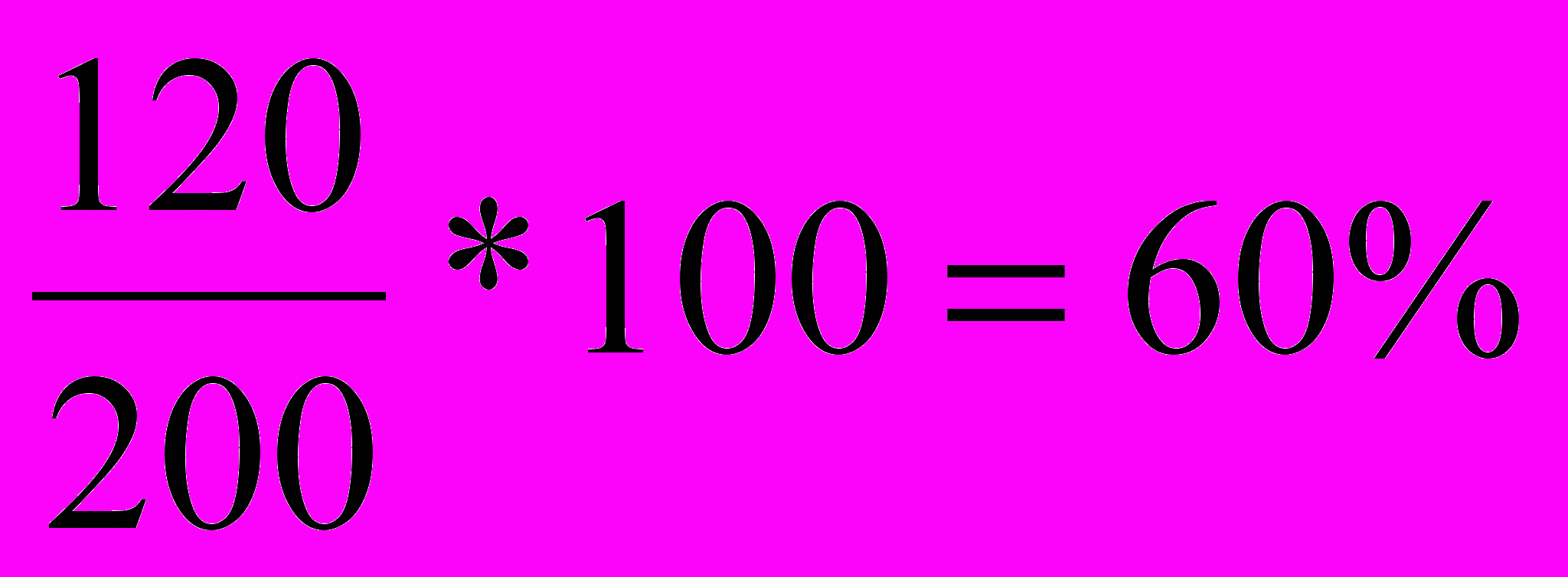- концентрация 2-го раствора. Ответ: 30%, 60%.

3. В сосуде было 20 л чистого спирта. Часть этого спирта отлили, а сосуд долили водой. Затем отлили столько же литров смеси и сосуд опять долили водой. После этого в сосуде оказалось чистого спирта втрое меньше, чем воды. Сколько спирта отлили в первый раз?

	Спирт	Вода	Общее кол-во раствор.
Было	20 л	-	20 л
Отлили	Х	-	х
Стало	20 – х	-	20 – х
Долили	-	х	х
Стало	20 – х	х	20
Отлили		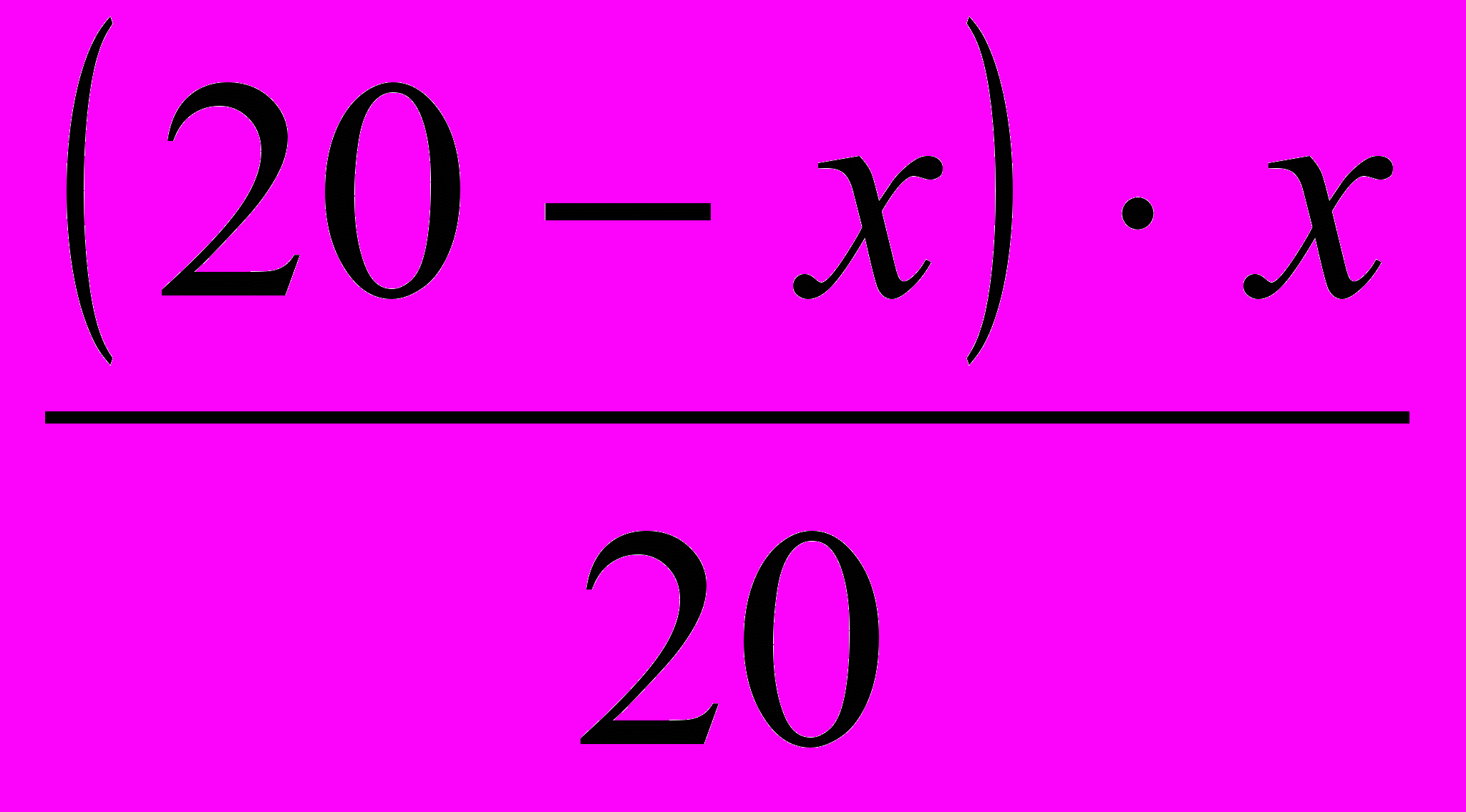	х
Стало Долили Стало	20 – х – (20 – х)*х/20 (20 - х)2/20 или 20/4	х	20 – х х 20

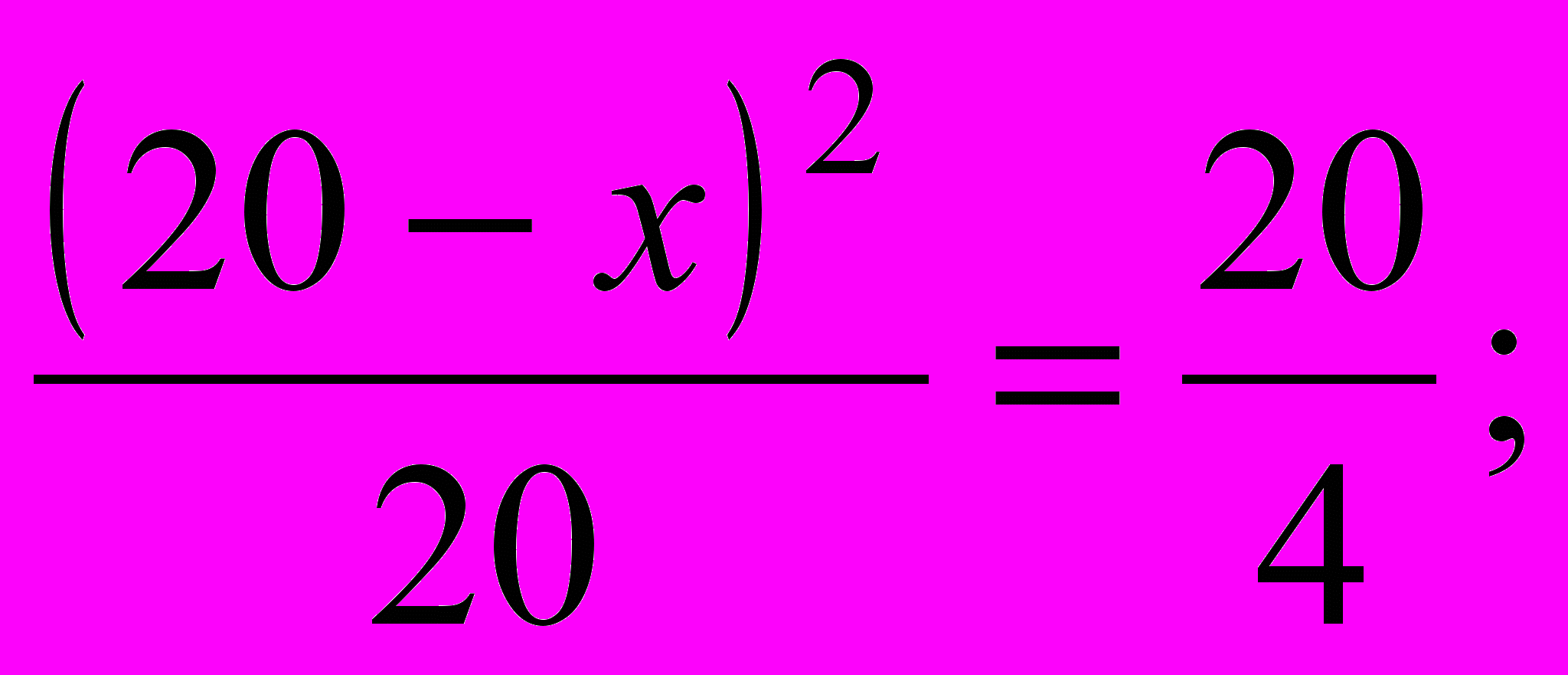
Решение: 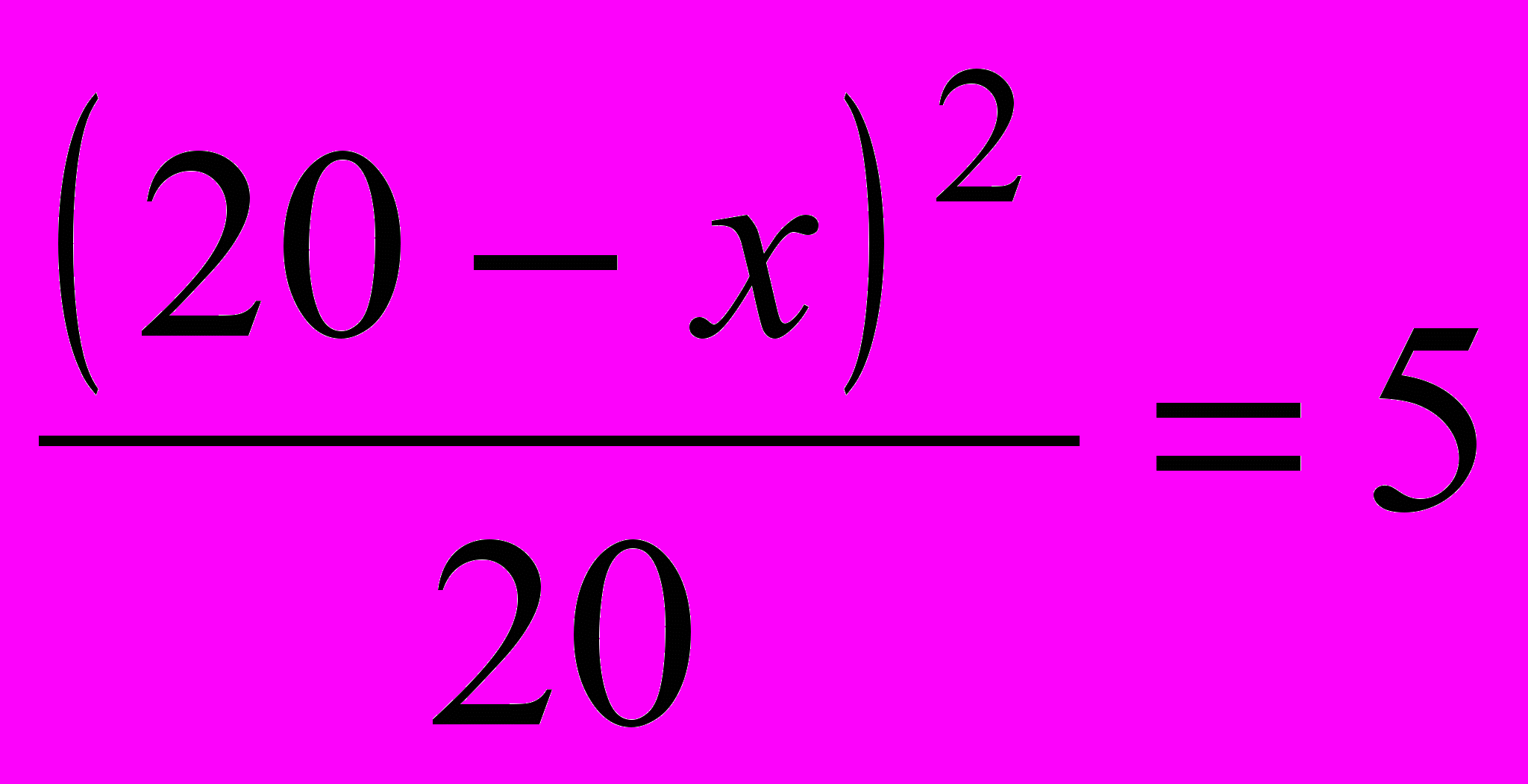; х² + 400 – 20 * 2х = 100

х₁ = 10, х₂ = 30; 30 л – не подходит по смыслу задачи.

Ответ: 10 л.

Можно рассуждать иначе. В результате двух переливаний в сосуде осталось 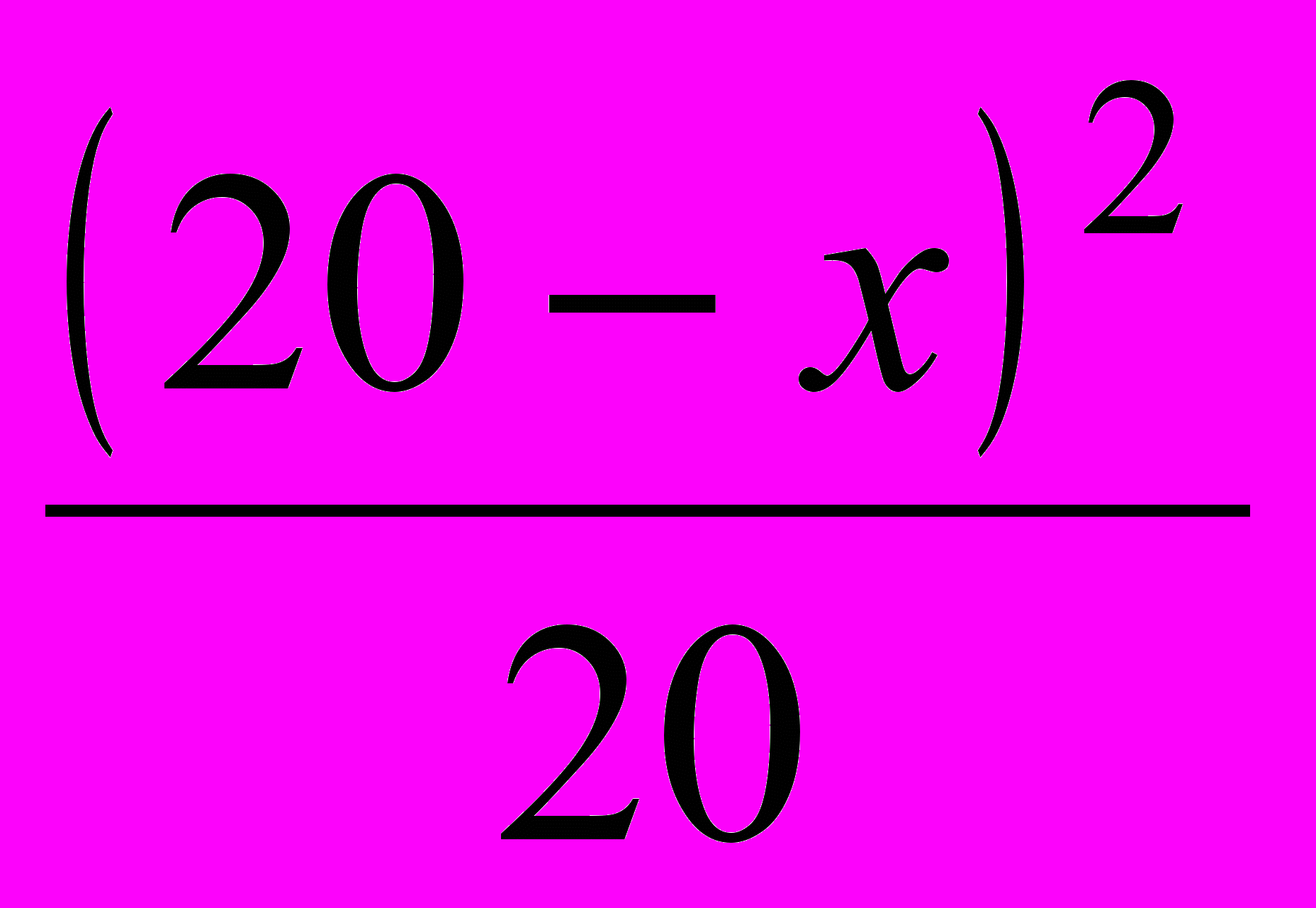чистого спирта, а концентрация его по отношению к раствору в сосуде будет 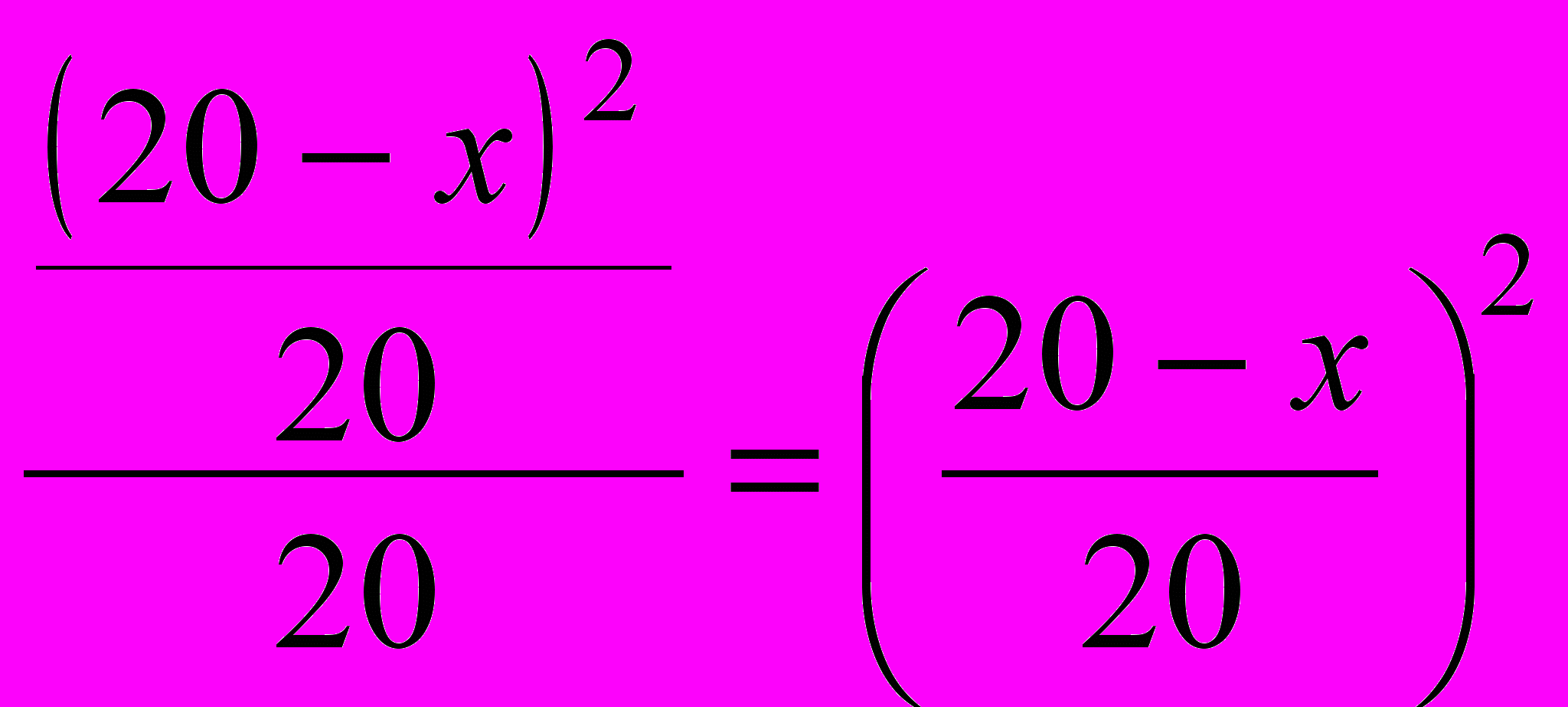. Если бы осуществляли еще одно переливание, то концентрация спирта определялась бы так: ...

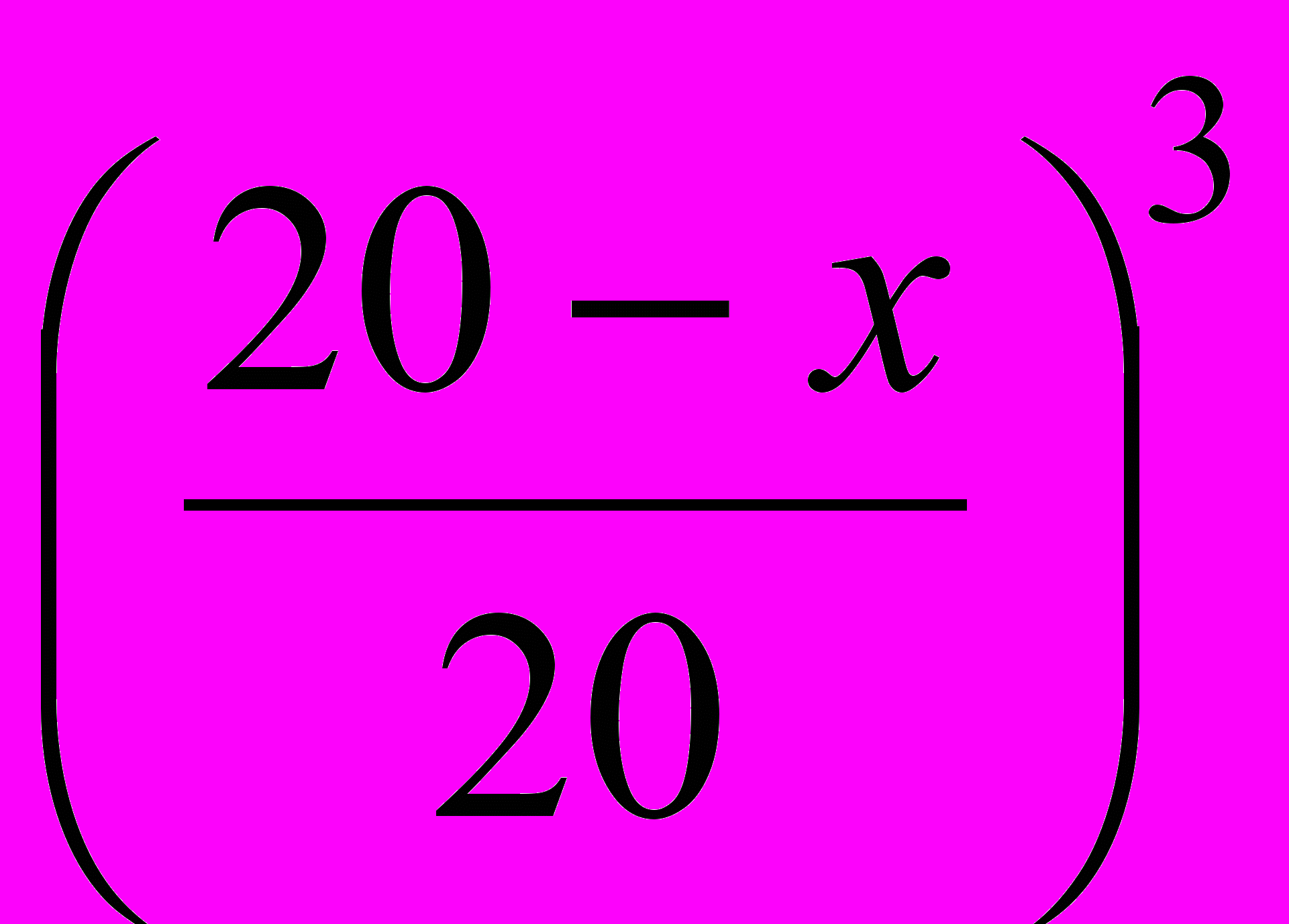Итак, концентрация представляет собой геометрическую прогрессию, где q₁ = 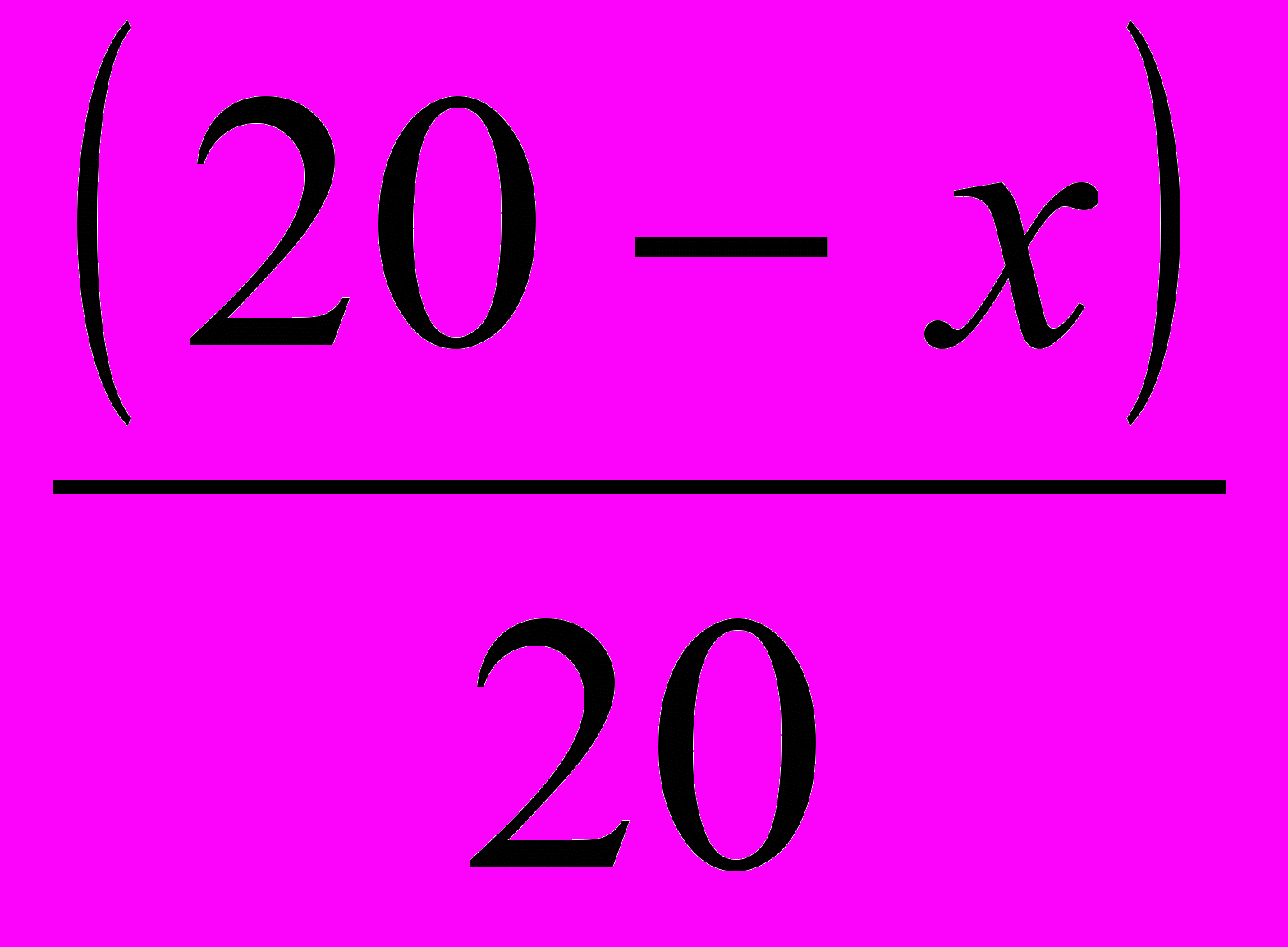, q₂ = q_{1 * 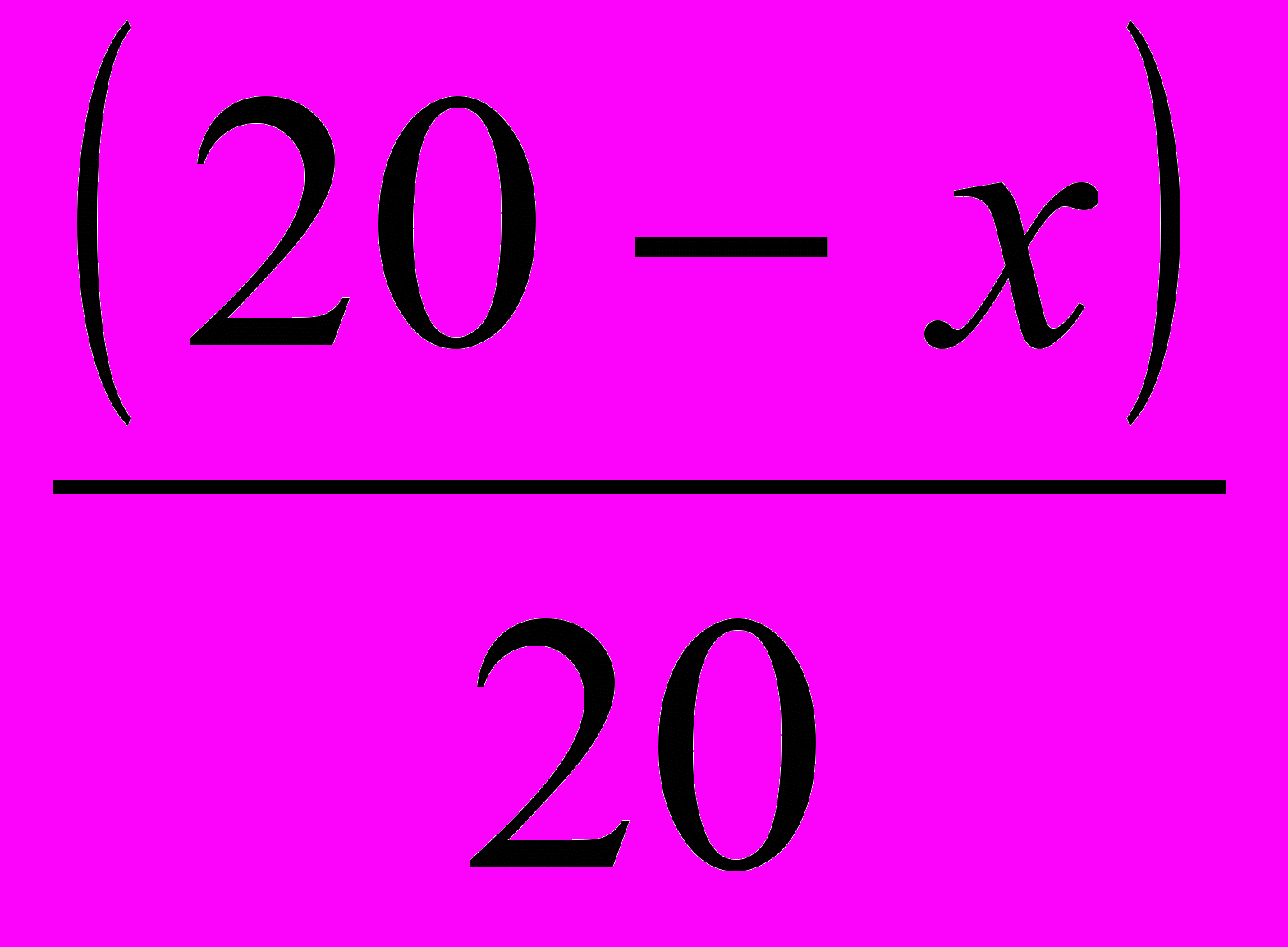, …}Поэтому эти задачи называют задачи на концентрацию и в них используют геометрическую прогрессию.

4. Из сосуда, содержащего чистый спирт, отлили 1/3 часть и добавили такое же количество воды. Потом отлили 1/3 часть смеси и добавили такое же количество воды. Так проделали k раз. (включая первое переливание). Какое наименьшее значение k, при котором содержание спирта в сосуде после сделанных переливаний станет меньше 10%.

	Спирт	Общее количество
Было	1	1
Отлили I	1/3	1/3
Стало	2/3	2/3
Добавили	-	1/3
Получили	2/3	1
Отлили II	1/3 * 2/3 = 2/9	1/3
Получили	2/3 – 2/9 = (2/3)2	2/3
Добавили Получили ... Получили k-й раз	- (2/3)2 (2/3)k	1/3 1 1

Решение:

F (k) = (2/3)^k; функция F (k) от аргумента 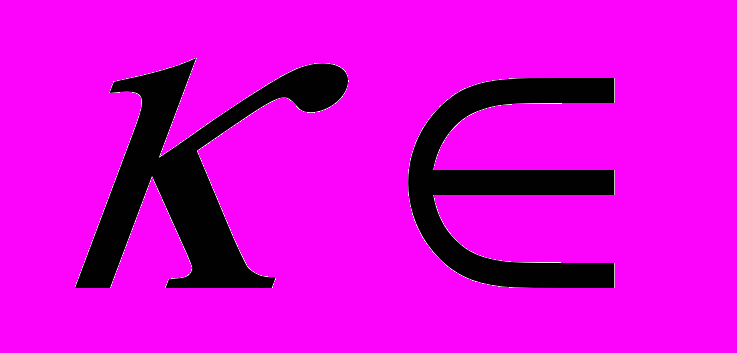N убывает, причем

F (5) = 32/243 >1/10; f (6) = 64/729 < 1/10,

поэтому наименьшее число k , для которого f (k) < 1/10 есть k = 6

Ответ: 6