План введение 2 раздел 1 анализ рынка услуг по доставке грузов 4 Характеристика транспортных услуг, оказываемых в московском регионе. 4

Вид материала

Документы

Содержание 3.3. Логистическая стратегия предприятия Мастера функций Математические/СуммаПроизвед

Подобный материал:

• V. тематика контрольных работ по дисциплине «стратегический менеджмент» и методические, 26.26kb.
• Техническое задание Запроса ценовых котировок на оказание услуг по транспортному обслуживанию, 49.1kb.
• Тематический план №№ п п. Наименование тем Введение в предмет. Понятийный аппарат, 69.77kb.
• Организация предпринимательской деятельности на автомобильном транспорте р 3112178-0393-00, 561.91kb.
• О моделировании взаимодействия железнодорожного и автомобильного транспорта при завозе-вывозе, 50.27kb.
• Тезисы доклада на тему: рынок транспортных услуг и безопасность, 121.05kb.
• Анализ регионального рынка Образовательных услуг: маркетинговый подход, 169.85kb.
• Формирование и развитие рынка информационных услуг в регионе (на материалах Ставропольского, 503.68kb.
• Инновационная культура как фактор успешного функционирования компании на рынке рекрутинговых, 93.68kb.
• Отчет о результатах деятельности Муниципального общеобразовательного автономного учреждения, 284.1kb.

3.3. Логистическая стратегия предприятия

На сегодняшний день, многие предприятия не осуществляют ни стратегического, ни перспективного финансового планирования, снижая тем самым вероятность своего выживания в сложившихся условиях. В большинстве случаев финансовый план разрабатывается только на ближайший квартал. Составляемые планы носят фрагментарный несистемный характер, разрабатываются на разной информационной базе, не содержат механизмов корректировки в процессе их реализации, что, на наш взгляд, приводит к рассогласованности и дезорганизации работы подразделений предприятия.

    Планирование, в свою очередь, должно основываться на адекватном использовании руководителями полученной информации обо всех параметрах деятельности предприятия. Таким образом, основой правильных решений является информация.

Логистическая стратегия предприятия, являясь составной частью общей корпоративной стратегии, состоит из способов действия, связанных с управлением цепью поставок и включает в себя постановку целей, способы  их достижения и мероприятия по рациональному управлению и координации товарно-материальных и связанных с ними потоков для реализации целей предприятия. Таким образом, логистическая стратегия вытекает из корпоративной стратегии предприятия, связывая общие цели с детальными операциями, выполняемыми в цепи поставок.

Прежде чем определить стратегию управления логистикой и цепями поставок, следует иметь объективную оценку текущего состояния, четко позиционировать логистическую функцию в структуре компании, выявить скрытые логистические издержки, определить требования к информационной системе управления цепями поставок и т. д. Для решения этих задач целесообразно создать проектную группу либо привлечь профессиональных логистов-аудиторов.

К сожалению, заставить производственные компании инвестировать в развитие управления цепями поставок, обучение кадров, привлечение сторонних специалистов и внедрение новых технологий невозможно. Так и сейчас проводятся конференции и семинары, создаются различные организации, целью которых является пропаганда технологий эффективного управления цепями поставок. Большую роль в этом направлении играет Supply Chain Council – международный Совет по цепям поставок.

Развитие логистики в России сопровождается сочетанием друг с другом современных торговых комплексов и старых неотапливаемых ангаров в качестве складов, разбитых дороги и профессионального управления цепями поставок. Противоречия неизбежны – слишком мало времени прошло с тех пор, как термин «логистика» вошел в обиход наших соотечественников. Многие компании начинают понимать всю значимость логистики в системе предприятия, ее прямое влияние на доходы предприятия, его инвестиционную привлекательность. Можно выделить семь основных тенденций, которые ставят вопросы логистики в список самых приоритетных задач для высшего руководства компаний.

Для многих компаний 25% розничной цены товаров народного потребления составляют затраты на цепи поставок, причем эта доля продолжает постоянно увеличиваться из-за возрастающей сложности логистических схем, изменения структуры заказов клиентов, повышения требований к качеству обслуживания клиентов. Увеличение издержек на логистику привлекает все более пристальное внимание со стороны руководства компании, и ведет к попыткам минимизировать издержки и увеличить прибыль.

Для решения логистической задачи, а также планирования маршрутов перевозок, когда Фирма имеет n складов (A1, A2,…, An) и m магазинов (B1, B2,…, Bm), известны объемы товаров на каждом складе ai (i=1,m) и размеры заказов товаров магазинами bj (j=1,n), а также транспортные издержки cij , связанные с перевозкой единицы товара со склада Ai в магазин Bj., следует произвести следующие действия:


Представим условие обеспечения заказов из магазинов товарами на складах уравнением.




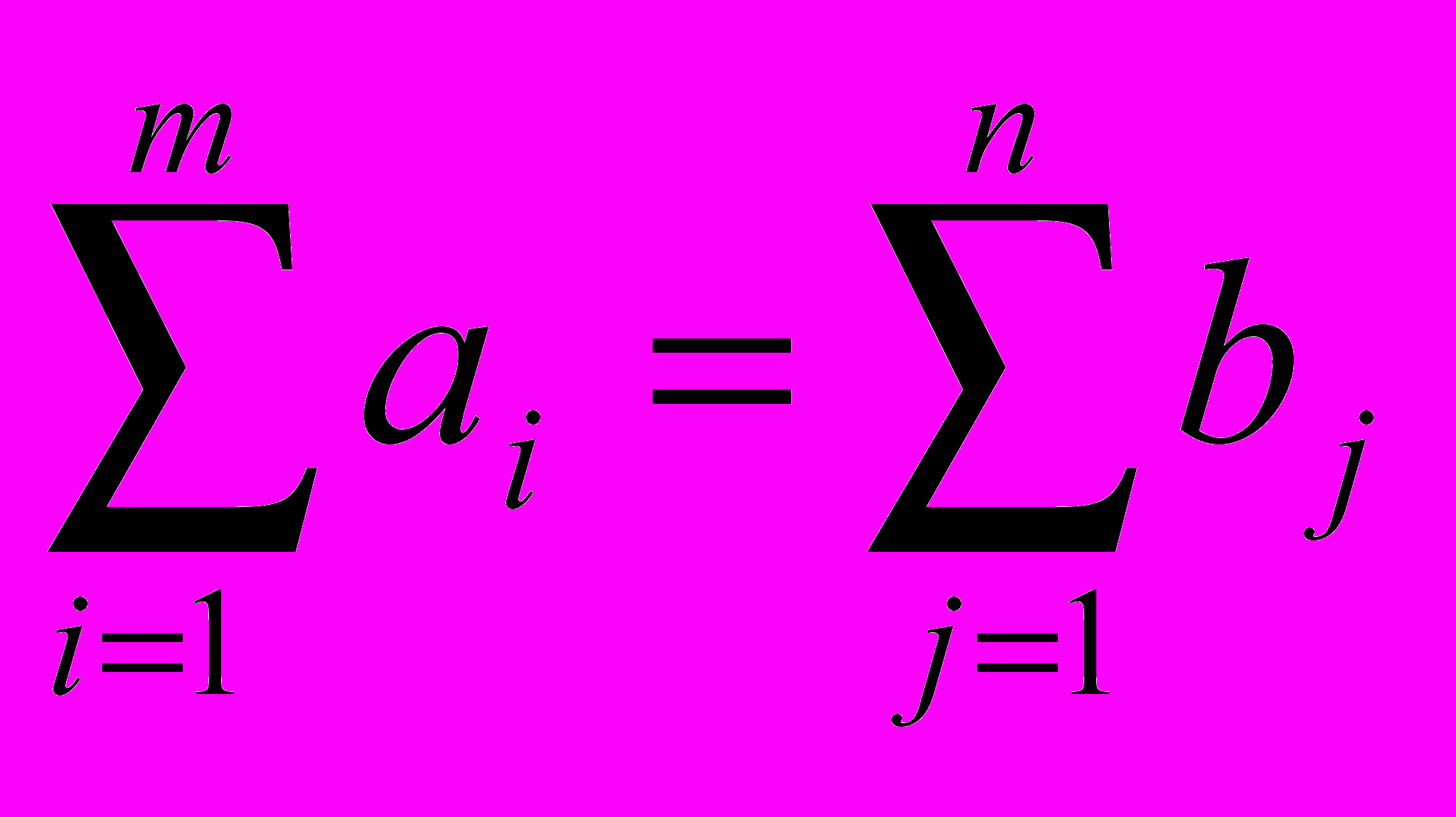
(3.3.1)


При условии полного баланса запасов товара и спроса транспортная задача называется замкнутой.


Построим математическую модель. Введем переменную xij - представляющую объем перевозимого товара со склада Ai в магазин Bj. Тогда условие удовлетворения спроса в каждом магазине запишется в виде





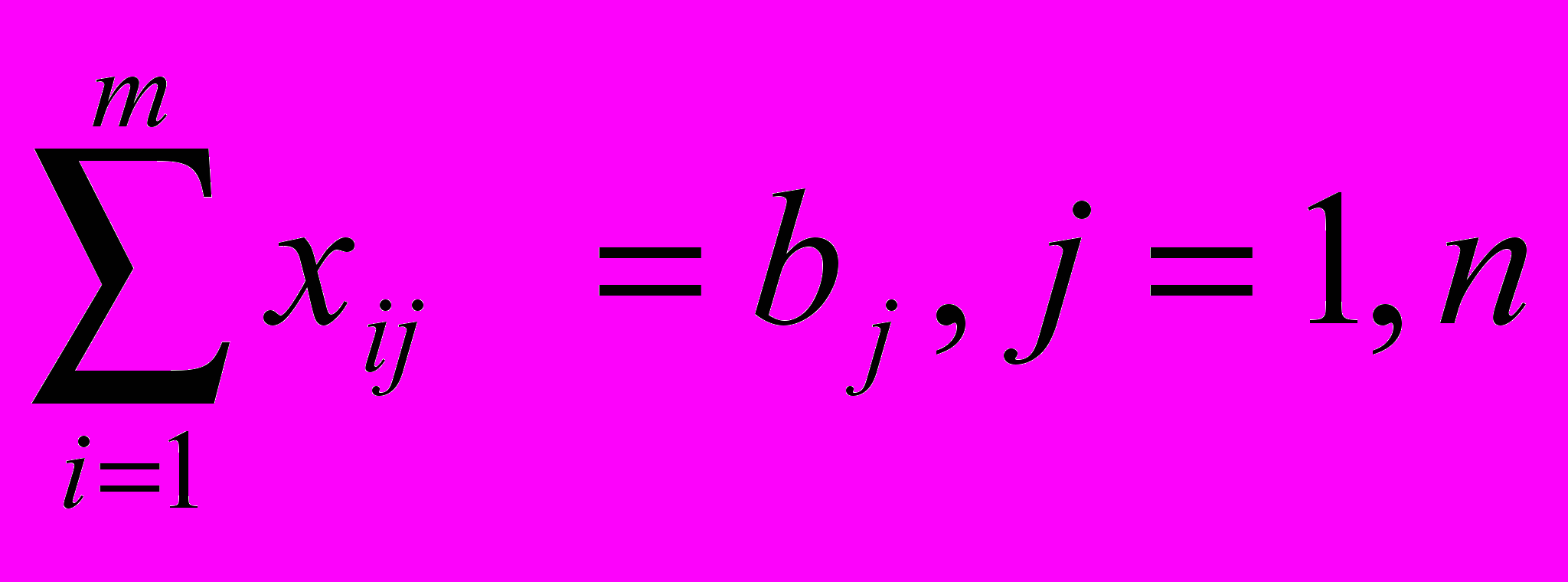
(3.3.2)

Условие вывоза со склада всех товаров запишем в виде




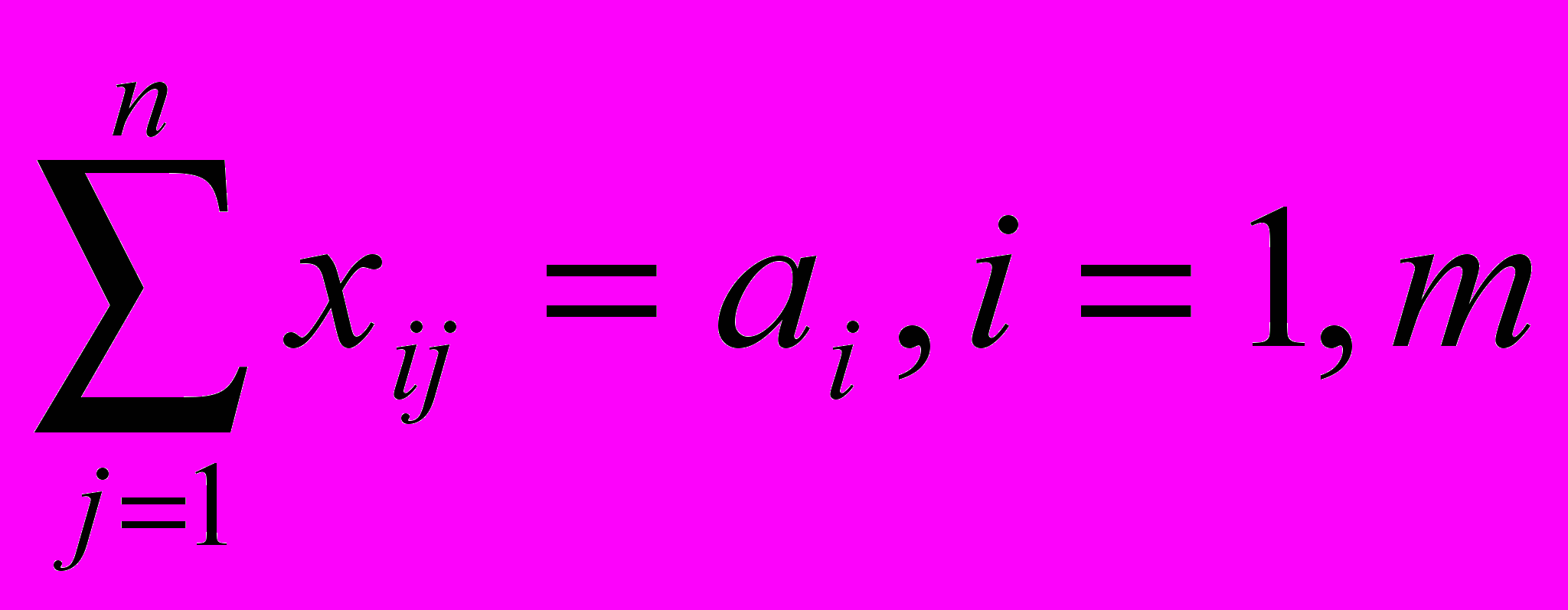
(3.3.3)


Обратные перевозки из магазинов на склады исключаются, поэтому объемы перевозимых товаров являются неотрицательными числами




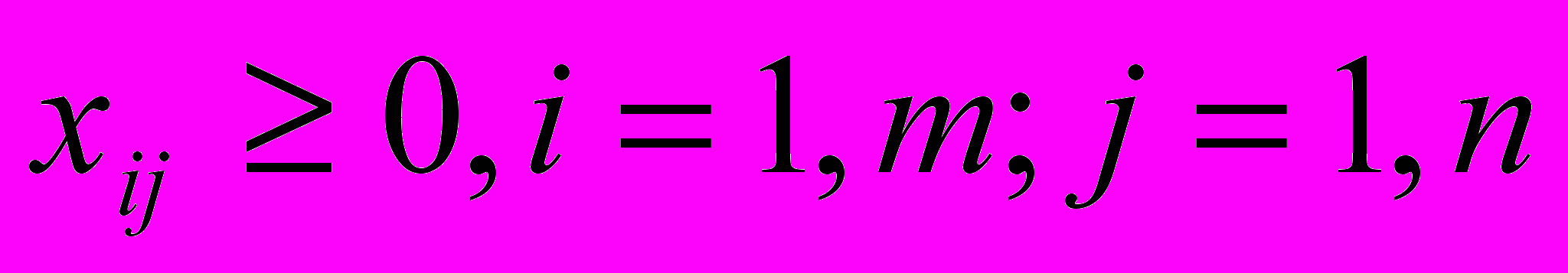
(3.3.4)

Транспортные издержки на перевозку со всех складов во все магазины представляются следующим уравнением




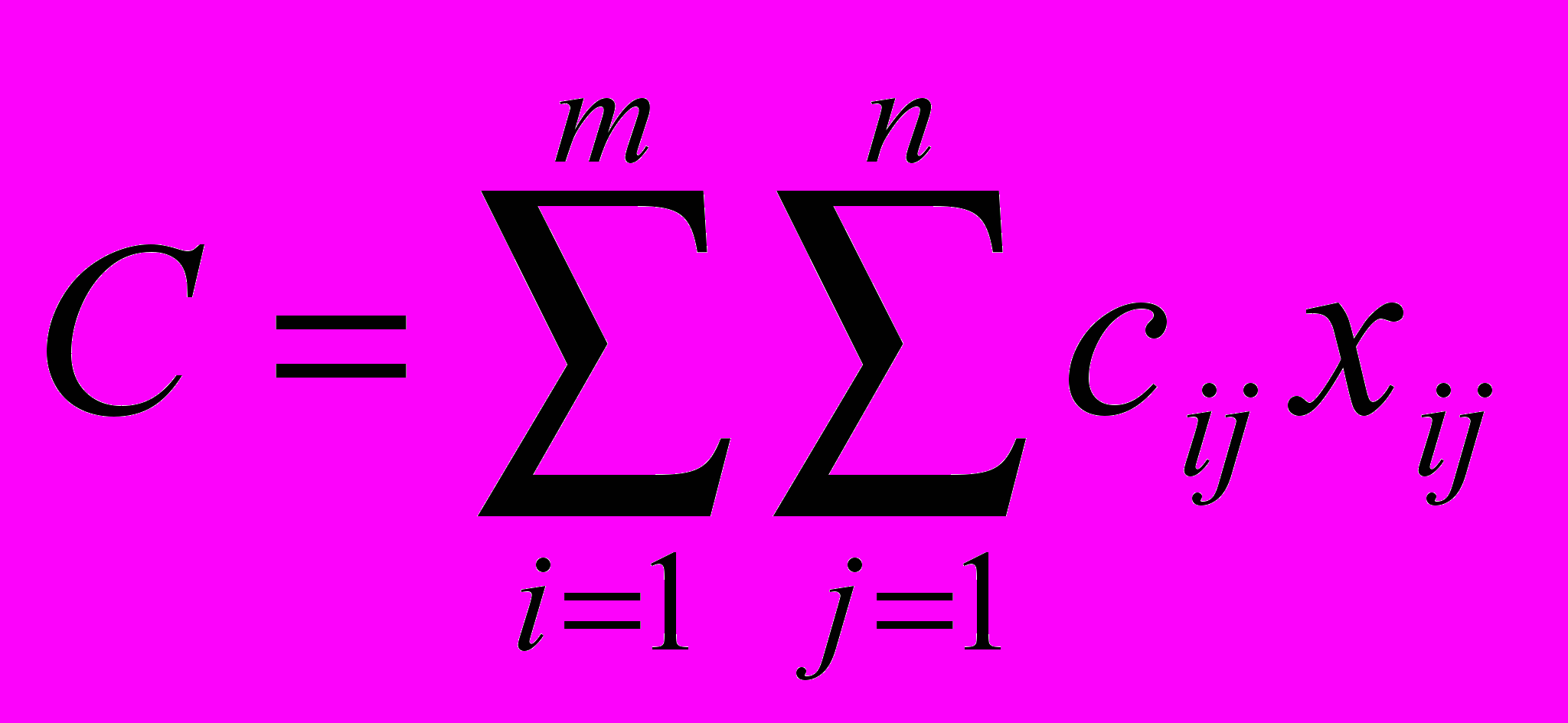
(3.3.5)


В терминах введенных обозначений транспортная задача формулируется следующим образом: требуется найти такие xij, для которых минимизируется функция C при соблюдении всех перечисленных ограничений.


Функция стоимости C (3.3.5) называется критерием оптимизационной задачи.


Имеются разновидности сформулированной задачи, когда уравнение (3.3.1) является неравенством. Это соответствует проблеме, когда заказы на товары от магазинов превышают суммарный объем товаров на складах или наоборот имеется избыток товаров на складах.


Такие транспортные задачи называются разомкнутыми и они сводятся к замкнутой транспортной задаче (3.3.1)-(3.3.5), являющейся базовой, путем изменения условий задачи. Такими изменениями могут быть введение дополнительных фиктивных складов или магазинов, что соответствует добавлению строк или столбцов в матрицу издержек.

Построим модель в электронной таблице для транспортной задачи. Пусть имеется 3 склада и 2 магазина, и транспортные издержки, между которыми приведены в табл.3.3.1.


Товары на складах/заказы магазинов и транспортные издержки Табл.3.3.1

Склады Магазины	a (45)	b (79)
A (18)	17	6
B (75)	12	13
C (31)	9	8

В скобках указаны запасы товаров на складах и заказы магазинов. На пересечении строк и столбцов указаны транспортные издержки при транспортировке единицы товара со склада в магазин.


Введем переменные xij (i=1,3; j=1,2), которые обозначают объемы перевозок с i-го склада в j-ый магазин.


С помощью переменных xij запишем ограничения для запасов на складах


x₁₁ + x₁₂ = 18,

x₂₁ + x₂₂ = 75, (3.3.6)

x₃₁ + x₃₂ = 31,


ограничения для запросов магазинов


x₁₁ + x₂₁ + x₃₁ = 45, (3.3.7)

x₁₂ + x₂₂ + x₃₂ = 79,


выражение для целевой функции

C = 17*x₁₁+12*x₂₁+9*x₃₁+6*x₁₂+13*x₂₂+8*x₃₂. (3.3.8)


Добавим еще два ограничения, отражающие условие, что все искомые переменные являются целыми и неотрицательными числами:


x₁₁0; x₂₁0; x₃₁0; x₁₂0; x₂₂0; x₃₂0 (3.3.9)


На рис.3.3.1 показано построение структуры модели в электронной таблице.



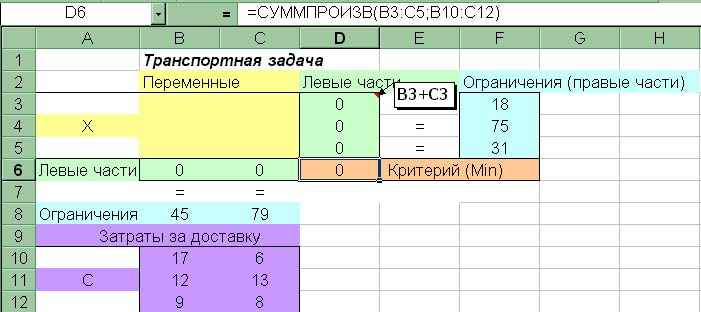
Рис.3.3.1. Модель транспортной задачи в электронной таблице


Модель состоит из 2-х таблиц Переменные и Затраты на доставку. В таблице Переменные для размещения переменных xij (i=1,3; j=1,2) отводится область (В3:С5). Значения переменных xij (i=1,3; j=1,2) вычисляются в результате моделирования.


В столбце D вычисляются левые части уравнений (3.3.6) по формуле D3= (B3+C3),…. Так как значения переменных xij (i=1,3; j=1,2) еще не вычислены, поэтому D3=D4=D5=0. В столбце F - указываются значения правых частей (3.3.6).


В строке 6 вычисляются левые части уравнений (3.3.7) по формуле В6= (B3+В4+В5),… Так как значения переменных не определены, то B6=C6=0. В строке 8 записываются значения правых частей (3.3.7).


Целевая функция (3.3.8) записана в ячейке D6. Ее формула показана во входной строке. Коэффициенты целевой функции С (транспортные издержки по доставке единицы товара со склада в магазин) записаны в таблице Затраты на доставку.


Формула для вычисления C определяется с помощью Мастера функций Математические/СуммаПроизвед. Далее для 1-го массива данных закрашивается область значений, отводимых для переменных x11,…,x32, (В3:С5) , а для второго массива данных закрашивается область коэффициентов целевой функции C (В10:С12) (рис.3.3.2).


Ограничения (3.3.9) указываются при настройке модели, как будет показано далее.




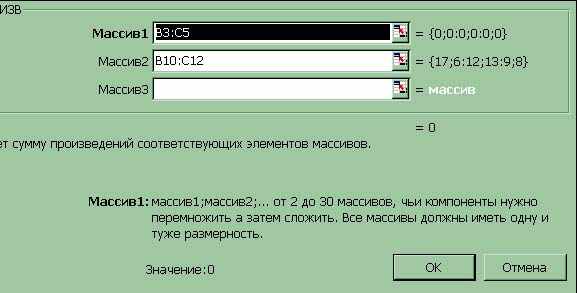
Рис.3.3.2. Построение формулы для вычисления целевой функции


После построения формул для целевой функции и левых частей переходят к настройке модели. Открывают в меню СервисПоиск решения (рис.3.3.3).



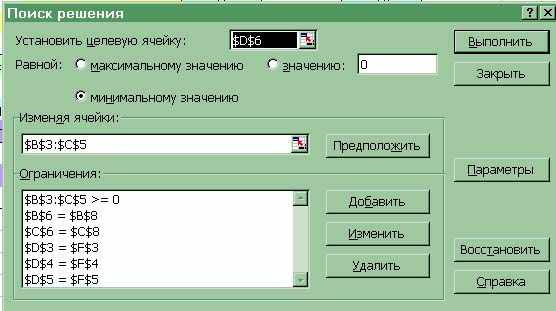
Рис.3.3.3. Настройка модели


В открывшемся меню производят следующие установки. Указывается адрес целевой функции C, что решение для минимального значения C. Указывается диапазон адресов для изменяемых переменных xij (i=1,3; j=1,2).


Ниже устанавливаются ограничения. Для этого нажимается клавиша Добавить (рис.3.3.4).




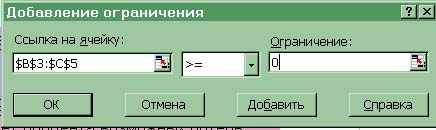
Рис.3.3.4. Пример записи ограничений для переменных x11,…x32 >=0


Аналогично записываются другие ограничения.


После записи всех ограничений (рис.3.3.3) переходят к выбору метода решения. Для этого нажимают клавишу Параметры (рис.3.3.5).




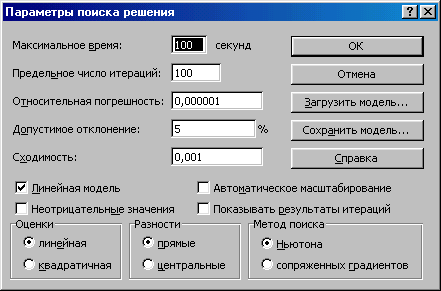
Рис.3.3.5. Выбор метода решения транспортной задачи


Установленные настройки подходят для большинства задач, поэтому их можно не изменять. В настройках следует указать Линейная модель и нажать клавишу ОК. Произойдет возврат к меню (рис.3.3.3). В нем осуществляется запуск модели нажатием клавиши Выполнить. Полученное решение показано на листе электронной таблицы (рис.3.3.6).



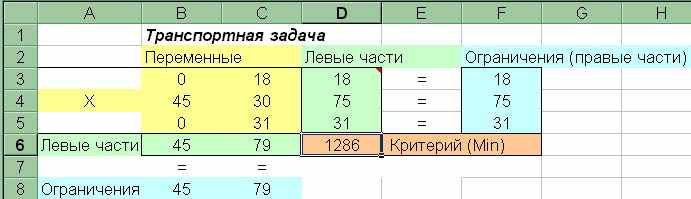
Рис.3.3.6. Решение транспортной задачи


Оптимальный план перевозок указан в таблице Переменные (В3:С5). План маршрутов перевозок представим в виде табл.3.3.2.


Оптимальный план перевозок товаров Табл.3.3.2

Склады Магазины	a (45)	b (79)
A (18)	0	18
B (75)	45	30
C (31)	0	31

При выполнении этого плана транспортные издержки – минимальны, и равны 1286 у.е.


Для анализа полученного решения используются отчеты по Результатам, Устойчивости и Пределам (рис.3.3.7).



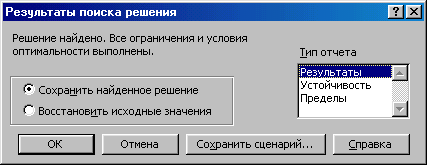
Рис.3.3.7. Вызов отчетов по Результатам, Устойчивости и Пределам


В данном случае для целочисленных решений создается только отчет по результатам (рис.3.3.8).



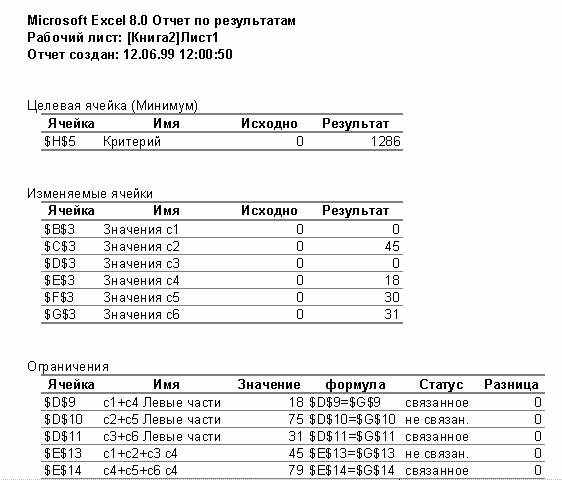
Рис.3.3.8. Фрагмент отчета по результатам


Для оценки выгоды, которую дает нахождение оптимального плана, можно построить диаграмму с минимальными и максимальными транспортными издержками (рис.3.3.9).




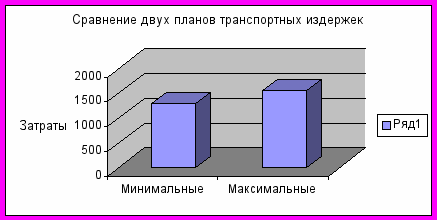
Рис.3.3.9. Сравнение максимальных и минимальных транспортных издержек


Минимальные издержки представляют оптимистический план перевозок, максимальные - пессимистический. Произведем расчет максимального выигрыша в случае использования рассмотренной модели (рис.3.3.10).




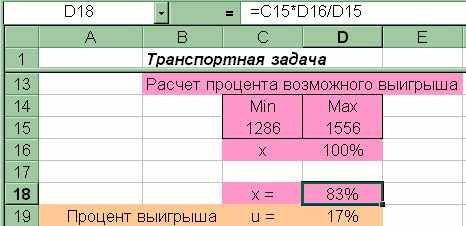
Рис.3.3.10. Расчет процента возможного выигрыша


В данной задаче выигрыш от применения компьютерной модели составляет 17%. В больших реальных задачах выигрыш может быть в несколько раз и даже в десятки раз.