Программа учебной дисциплины современный финансовый менеджмент
| Вид материала | Программа |
- Рабочая программа дисциплины современный менеджмент направление ооп: 080200 менеджмент, 305kb.
- Программа учебной дисциплины «Инвестиционный менеджмент», 200.94kb.
- Программа дисциплины дс. 01. «Финансовый менеджмент» для студентов специальности 080507, 227.28kb.
- Программа учебной дисциплины «Финансовый менеджмент», 190.02kb.
- Рабочая программа учебной дисциплины дисциплины «Финансовый инжиниринг» для направления, 169.96kb.
- Программа учебной дисциплины «Управление финансовыми рисками и производные инструменты», 178.02kb.
- Программа учебной дисциплины «Контроллинг в системе управления корпоративными финансами», 178.54kb.
- Рабочая программа учебной дисциплины «финансовый менеджмент» (название дисциплины), 694.08kb.
- Программа учебной дисциплины «Правовые аспекты управленческой деятельности» федерального, 153.8kb.
- Программа учебной дисциплины «Финансовый менеджмент» Для направления 080100. 62/ «Экономика», 423.95kb.
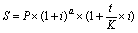 , (12)
, (12) где a – число полных лет в составе продолжительности операции,
t – число дней в отрезке времени, приходящемся на неполный год,
K –временная база.
В этом случае вновь возникает необходимость выполнения календарных вычислений по рассмотренным выше правилам. Например, ссуда в 3 млн. рублей выдается 1 января 1997 года по 30 сентября 1999 года под 28% годовых (процентная ставка). В случае начисления сложных процентов за весь срок пользования деньгами наращенная сумма составит:
S = 3 * (1 + 0,28)(2 + 9/12) = 5,915 млн. рублей
Если же использовать смешанный способ (например, коммерческие проценты с точным числом дней), то получим:
S = 3 * (1 + 0,28)2 * (1 + 272 / 360 * 0,28) = 6 млн. рублей
Таким образом, щепетильность кредитора в данном случае оказалась вовсе не излишней и была вознаграждена дополнительным доходом в сумме 85 тыс. рублей.
Важной особенностью сложных процентов является зависимость конечного результата от количества начислений в течение года. Здесь опять сказывается влияние реинвестирования начисленных процентов: база начисления возрастает с каждым новым начислением, а не остается неизменной, как в случае простых процентов. Например, если начислять 20% годовых 1 раз в год, то первоначальная сумма в 1 тыс. рублей возрастет к концу года до 1,2 тыс. рублей (1 * (1+ 0,2)). Если же начислять по 10% каждые полгода, то будущая стоимость составит 1,21 тыс. рублей (1 * (1 + 0,1) * (1 + 0,1)), при поквартальном начислении по 5% она возрастет до 1,216 тыс. рублей. По мере увеличения числа начислений (m) и продолжительности операции эта разница будет очень сильно увеличиваться. Если разделить сумму начисленных процентов при ежеквартальном наращении на первоначальную сумму, то получится 21,6% (0,216 / 1 * 100), а не 20%. Следовательно сложная ставка 20% при однократном наращении и 20% (четыре раза по 5%) при поквартальном наращении приводят к различным результатам, то есть они не являются эквивалентными. Цифра 20% отражает уже не действительную (эффективную), а номинальную ставку. Эффективной процентной ставкой является значение 21,6%. В финансовых расчетах номинальную сложную процентную ставку принято обозначать буквой j. Формула наращения по сложным процентам при начислении их m раз в году имеет вид:
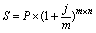 , (13)
, (13) Например ссуда размером 5 млн. рублей выдана на 2 года по номинальной сложной процентной ставке 35% годовых с начислением процентов 2 раза в год. Будущая сумма к концу срока ссуды составит:
S = 5 * (1 + 0,35 / 2)(2 * 2) = 9,531 млн. рублей.
При однократном начислении ее величина составила бы лишь 9,113 млн. рублей (5 * (1 + 0,35)2; зато при ежемесячном начислении возвращать пришлось бы уже 9,968 млн. рублей (5 * 1 + (0,35 / 12)(12 * 2)).
При начислении антисипативных сложных процентов, номинальная учетная ставка обозначается буквой f, а формула наращения принимает вид:
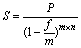 (14)
(14) Выражение 1 / (1 – f / m)mn множитель наращения по номинальной учетной ставке.
Дисконтирование по сложным процентам также может выполняться двумя способами – математическое дисконтирование и банковский учет. Последний менее выгоден для кредитора, чем учет по простой учетной ставке, поэтому используется крайне редко. В случае однократного начисления процентов его формула имеет вид:
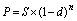 , (15)
, (15) где (1 –d)n – дисконтный множитель банковского учета по сложной учетной ставке.
при m > 1 получаем
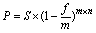 , (16)
, (16) где f – номинальная сложная учетная ставка,
(1 – f / m)mn – дисконтный множитель банковского учета по сложной номинальной учетной ставке.
Значительно более широкое распространение имеет математическое дисконтирование по сложной процентной ставке i. Для m = 1 получаем
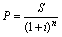 , (17)
, (17) где 1 / (1 + i)n – дисконтный множитель математического дисконтирования по сложной процентной ставке.
При неоднократном начислении процентов в течение года формула математического дисконтирования принимает вид:
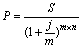 , (18)
, (18) где j –номинальная сложная процентная ставка,
1 / (1 + j / m)mn – дисконтный множитель математического дисконтирования по сложной номинальной процентной ставке.
Например, требуется определить современную стоимость платежа в размере 3 млн. рублей, который должен поступить через 1,5 года, процентная ставка составляет 40%:
при m = 1 P = 3 / (1 + 0,4)1,5 = 1,811 млн. рублей
при m = 2 (начисление 1 раз в полугодие) P = (3 / (1 + 0,4 / 2)(2 * 1,5) = 1,736 млн. рублей
при m = 12 (ежемесячное начисление) P = (3 / (1 + 0,4 / 12)(12 * 1,5) = 1,663 млн. рублей.
По мере увеличения числа начислений процентов в течение года (m) проежуток времени между двумя смежными начислениями уменьшается – при m = 1 этот промежуток равен 1 году, а при m = 12 – только 1 месяцу. Теоретически можно представить ситуацию, когда начисление сложных процентов производится настолько часто, что общее его число в году стремится к бесконечнности, тогда величина промежутка между отдельными начислениями будет приближаться к нулю, то есть начисление станет практически непрерывным. Такая на первый взгляд гипотетическая ситуация имеет важное значение для финансов и при построении сложных аналитических моделей (например при разработке масштабных инвестиционных проектов) часто применяют непрерывные проценты. Непрерывная процентная ставка (очевидно, что при непрерывном начислении речь может идти только о сложных процентах) обозначается буквой δ (читается “дельта”), часто этот показатель называют “сила роста”. Формула наращения по непрерывной процентной ставке имеет вид:
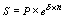 , (19)
, (19) где e – основание натурального логарифма (≈2,71828...),
en – множитель наращения непрерывных процентов.
Например, чему будет равна через 3 года сумма 250 тыс. рублей, если сегодня положить ее на банковский депозит под 15% годовых, начисляемых непрерывно?
S = 250 * e(0,15 * 3) = 392,1 тыс. рублей.
Для непрерывных процентов не существует различий между процентной и учетной ставками – сила роста является универсальным показателем. Однако, наряду с постоянной силой роста может использоваться переменная процентная ставка, величина которой меняется по заданному закону (математической функции). В этом случае можно строить очень мощные имитационные модели, однако математический аппарат расчета таких моделей достаточно сложен и не рассматривается в настоящем пособии, так же как и начисление процентов по переменной непрерывной процентной ставке.
Непрерывное дисконтирование с использованием постоянной силы роста выполняется по формуле:
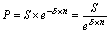 , (20)
, (20) где 1 / en – дисконтный множитель дисконтирования по силе роста.
Например, в результате осуществления инвестиционного проекта планируется получить через 2 года доход в размере 15 млн. рублей. Чему будет равна приведенная стоимость этих денег в сегодняшних условиях, если сила роста составляет 22% годовых?
P = 15 / e(0,22 * 2) = 9,66 млн. рублей.
2. Эквивалентность процентных ставок.
Эквивалентными называются ставки, наращение или дисконтирование по которым приводит к одному и тому же финансовому результату. Например, в условиях последнего примера эквивалентными являются простая процентная ставка 200,3% и сложная процентная ставка 511,6%, т.к. начисление любой из них позволяет нарастить первоначальную сумму 8,2 тыс. рублей до 10 тыс. рублей за 40 дней. Приравнивая между собой множители наращения (дисконтирования), можно получить несложные формулы эквивалентности различных ставок. Для удобства эти формулы представлены в табличной форме. В заголовки граф табл. 3.2.2 помещены простые процентная (i) и учетная (d) ставки. В заголовках строк этой таблицы указаны все рассмотренные в данном пособии ставки. На пересечении граф и столбцов приводятся формулы эквивалентности соответствующих ставок. В таблицу не включены уравнения эквивалентности простых процентных и сложных учетных ставок, вследствие маловероятности возникновения необходимости в таком сопоставлении.
Знание уравнений эквивалентности позволяет без труда переходить от одного измерения доходности к другому. Например, доходность облигаций по простой процентной ставке составила за полгода 60%. По формуле (21) найдем, что в пересчете на сложные проценты это составляет 69%. Доходность векселя, дисконтированного по простой учетной ставке 50% за 3 месяца до срока погашения, в пересчете на простую процентную ставку составит 57,14% (34), если же по процентной ставке принята точная временная база (365 дней), то применив формулу (36), получим i = 57,94%).
Таблица 1.
Эквивалентность простых ставок
| | Простая процентная ставка (iпр) | Простая учетная ставка (dпр) |
| Сложная процентная ставка (iсл) |  (20) (20) 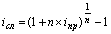 (21) (21) | 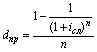 (22) (22) 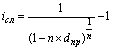 (23) (23) |
| Сложная номинальная процентная ставка (j) | 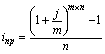 (24) (24) 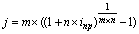 (25) (25) | 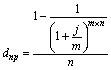 (26) (26) 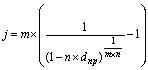 (27) (27) |
| Сила роста () | 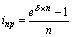 (28) (28) 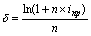 (29) (29) | 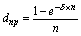 (30) (30) 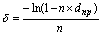 (31) (31) |
| Простая учетная ставка (dпр) n = t / K | 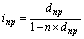 (32) (32) 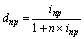 (33) (33) | – |
| Простая учетная ставка (dпр) ki = kd = 360 | 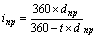 (34) (34) 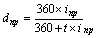 (35) (35) | – |
| Простая учетная ставка (dпр) ki = 365 kd = 360 | 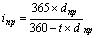 (36) (36) 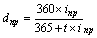 (37) (37) | – |
Например, предприятие может столкнуться с необходимостью выбора между получением кредита на 5 месяцев под сложную номинальную ставку 24% (начисление процентов поквартальное) и учетом в банке векселя на эту же сумму и с таким же сроком погашения. Небходимо определить простую учетную ставку, которая сделает учет векселя равновыгодной операцией по отношению к получению ссуды. По формуле (26) получим d = 22,21%.
Таблица 2.
Эквивалентность сложных процентных ставок
| | Сложная процентная ставка (iсл) | Сложная учетная ставка (dсл) |
| Сложная номинальная процентная ставка (j) | 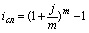 (39) (39) 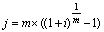 (40) (40) | 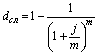 (41) (41)  (42) (42) |
| Сила роста () | 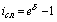 (43) (43) 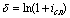 (44) (44) | Сложная номинальная процентная ставка (j) |
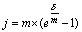 (45) (45) 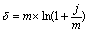 (46) (46) | ||
| Сложная учетная ставка (dсл) | 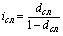 (47) (47) 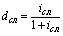 (48) (48) | – |
Например, по вкладу в размере 10 тыс. рублей начисляется 25 простых процентов в год. В конце 1 года вклад возрастет до 12500 рублей. Доходность, измеренная как по простой (формула 12), так и сложной (15) процентной ставке i, составит 25% годовых. Однако, измеряя доходность по номинальной ставке j (16) при m = 2, получим лишь 23,61%, т.к. в этом случае будет учтена потерянная вкладчиком возможность реинвестирования процентов хотя бы 2 раза в год. Если же измерить доходность по силе роста (19), то она окажется еще ниже – всего 22,31%, т.к. теоретически он мог реинвестировать начисленные проценты не 2 раза в год, а непрерывно.
3. Аннуитет.
В финансовом анализе для обозначения денежных потоков в наиболее общем смысле используется термин рента. Каждый отдельный рентный платеж называют членом ренты. Частным случаем ренты является финансовая рента или аннуитет – такой поток платежей, все члены которого равны друг другу, так же как и интервалы времени между ними. Часто аннуитетом называют финансовый актив, приносящий фиксированный доход ежегодно в течение ряда лет. В буквальном переводе “аннуитет” подразумевает, что платежи происходят с интервалом в один год, однако встречаются потоки с иной периодичностью выплат. Очевидно, что рента – это более широкое понятие, чем аннуитет, так как существует множество денежных потоков, члены которых не равны друг другу или распределены неравномерно.
Форму аннуитетов имеют многие финансовые потоки, например выплата доходов по облигациям или платежи по кредиту, страховые взносы и др. Можно сказать, что финансы тяготеют к упорядочению денежных потоков. Это и понятно, так как равномерность любых процессов связана с их упорядоченностью, а следовательно – предсказуемостью и определенностью. И хотя риск как мера неопределенности постоянно присутствует в финансах, однако с увеличением этого риска происходит трансформация финансовой деятельности в индустрию азартных игр. Различие между двумя ценными бумагами (облигацией, имеющей высокий рейтинг, и лотерейным билетом) состоит именно в том, что первая из них с достаточно высокой вероятностью гарантирует ее владельцу возникновение упорядоченного положительного денежного потока (аннуитета).
Принцип временной ценности денег делает невозможным прямое суммирование членов ренты. Для учета влияния фактора времени к каждому члену ренты применяются рассмотренные выше правила наращения и дисконтирования. Причем в анализе денежных потоков применяется техника вычисления только сложных процентов, то есть предполагается, что получатель потока имеет возможность реинвестировать получаемые им суммы.. Если бы размеры рент всегда ограничивались двумя-тремя членами, то необходимость создания специальных способов расчета денежных потоков, возможно, и не возникла. Ни в теории ни на практике таких ограничений нет, наоборот, существуют большие, очень большие и даже бесконечные денежные потоки (вечные ренты), поэтому были разработаны специальные методы, позволяющие анализировать ренту не по каждому ее члену в отдельности, а как единую совокупность – рассчитывать ее будущую и приведенную величины, а также определять размеры других важных параметров ренты.
Как уже отмечалось ранее, в процессе начисления сложных процентов на единичную сумму P возникает геометрическая прогрессия со знаменателем (1 + i), наращенная сумма S представляет собой последний член этой прогрессии P * (1 + i)n. Денежный поток представляет собой совокупность таких единичных сумм Pk, поэтому наращение денежного потока означает нахождение суммы всех k последних членов геометрических прогрессий, возникающих по каждому из них. В случае аннуитета задача упрощается, т.к. Pk в этом случае будет постоянной величиной = P. То есть возникает одна геометрическая прогрессия с первым членом P и знаменателем (1 + i). Отличие от сложных процентов для единичного платежа здесь заключается в том, что требуется найти не последний член прогрессии, а ее сумму. В случае дисконтирования аннуитета меняется лишь знаменатель прогрессии – он будет равен не (1 + i), а 1 / (1 + i). Приведенная стоимость аннуитета находится как сумма вновь полученной геометрической прогрессии.
Наряду с членом ренты (обозначим его R) любой денежный поток характеризуется рядом других параметров: период ренты (t) – временной интервал между двумя смежными платежами; срок ренты (n) – общее время, в течение которого она выплачивается; процентная ставка (i) – ставка сложного процента, используемая для наращения и дисконтирования платежей, из которых состоит рента; число платежей за 1 период ренты (p) – используется в том случае, если в течение 1 периода ренты, производится больше, чем 1 выплата денежных средств; число начислений процентов в течение 1 периода ренты (m) – при начислении (дисконтировании) по номинальной процентной ставке (j).
В зависимости от числа платежей за период различают годовые и p-срочные ренты. В первом случае за 1 период ренты (равный, как правило 1 году) производится 1 выплата; во втором, в течение периода производится p выплат (p > 1). В случае очень частых выплат, рента может рассматриваться как непрерывная (p → ∞); значительно чаще в финансовом анализе имеют дело с дискретными рентами, для которых p – конечное целое число. Так же как и при использовании сложной процентной ставки для единичных сумм, наращение (дисконтирование) рент может производиться 1 раз за период, m раз за период или непрерывно. По величине членов денежного потока ренты могут быть постоянными (с равными членами) и переменными. По вероятности выплат ренты делятся на верные и условные. В случае условной ренты выплата ее членов ставится в зависимость от наступления какого-либо условия. По своей общей продолжительности (или по числу членов) различают ограниченные (с конечным числом членов) и бесконечные (вечные, бессрочные) ренты. По отношению к фиксированному моменту начала выплат ренты могут быть немедленными и отложенными (отсроченными). Ренты, платежи по которым производятся в конце периода называются обычными или постнумерандо; при выплатах в начале периода говорят о рентах пренумерандо.
Рассмотрим пример определения будущей величины ограниченной постоянной ренты (аннуитета) постнумерандо которая выплачивается 1 раз в год (p = 1) и проценты по которой начисляются по сложной эффективной процентной ставке i 20% годовых также 1 раз в год (m = 1). Размер годового платежа R составляет 3 тыс. рублей, общий срок ренты n равен 5 годам.
Наращение денежного потока
Таблица 3.
| № периода | 1 | 2 | 3 | 4 | 5 | Итого |
| 1.Член ренты, тыс. руб. | 3 | 3 | 3 | 3 | 3 | 15 |
| 2.Время до конца ренты, периодов (лет) | 4 | 3 | 2 | 1 | 0 | – |
| 3.Множитель наращения | (1+0,2)4 | (1+0,2)3 | (1+0,2)2 | (1+0,2)1 | (1+0,2)0 | – |
| 4.Наращенная величина, тыс. руб. (стр.1*;стр.3) | 6,22 | 5,18 | 4,32 | 3,6 | 3 | 22,32 |
Полученное значение (22,32 тыс. руб.) заметно больше арифметической суммы отдельных членов ренты (15 тыс. руб.), однако она значительно меньше той гипотетической суммы, которая могла быть получена, если бы мы захотели нарастить по ставке 20% все 15 тыс. руб. за весь срок ренты (15*; 1,25). Наращенная сумма ренты S получена путем последовательного начисления процентов по каждому члену ренты и последующего суммирования полученых результатов. Введя обозначение k = номеру периода ренты, в наиболее общей форме данный процесс можно выразить следующей формулой:
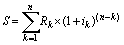 (1)
(1) В нашем примере член ренты R неизменен в течение всего срока, процентная ставка i также постоянна. Поэтому наращенную величину ренты можно найти как сумму геометрической прогрессии с первым членом 3000 и знаменателем (1 + 0,2):
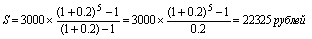
Следовательно, от общей формулы наращения ренты (1) можно перейти к ее частному случаю – формуле наращения аннуитета:
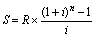 (2)
(2) Второй сомножитель этого выражения – ((1 + i)n – 1) / i – называется множителем наращения аннуитета. Так же как и в случае с начислением процентов на единичные суммы, значения таких множителей табулированы, что позволяет облегчить процентные вычисления денежных потоков.
Наращение денежных потоков имеет место при периодическом внесении на банковский депозит фиксированных сумм с целью накопления финансового фонда к определенному моменту времени. Например, разместив долгосрочный облигационный заем, предприятие готовится к погашению суммы основного долга в конце срока займа путем периодического внесения на банковский счет фиксированных платежей под установленный процент. Таким образом к моменту погашения облигационного займа у предприятия накопятся достаточные средства в этом фонде. Аналогичные задачи решаются в ходе формирования пенсионного фонда или при накоплении суммы для оплаты обучения детей. Например, заботясь о своей старости, человек может наряду с обязательными отчислениями в государственный Пенсионный фонд, вносить часть своего ежемесячного заработка на банковский депозит под проценты. Наращение суммы такого вклада будет происходить по описанному выше алгоритму. Таким же путем предприятия могут формировать амортизационный фонд для плановой замены оборудования.
Обратный по отношению к наращению процесс – дисконтирование денежного потока имеет еще большую важность для финансового менеджмента, так как в результате определяются показатели, являющиеся в настояее время основными критериями принятия финансовых решений. Рассмотрим этот процесс более подробно. Предположим, что рассмотренный в нашем примере денежный поток характеризует планируемые поступления от реализации инвестиционного проекта. Доходы должны поступать в конце периода. Так как эти поступления планируется получить в будущем, а инвестиции, необходимые для выполнения проекта, должны быть произведены уже сегодня, предприятию необходимо сопоставить величину будущих доходов с современной величиной затрат. Как уже было сказано выше, использование для сравнения арифметической суммы членов потока (15 тыс. руб.) бессмысленно, так как эта сумма не учитывает влияние фактора времени. Для обеспечения сопоставимости данных величина будущих поступлений должна быть приведена к настоящему моменту, иными словами данный денежный поток должен быть дисконтирован по ставке 20%. Предприятие сможет определить сегодняшнюю стоимость будущих доходов. При этом процентная ставка будет выступать в качестве измерителя альтернативной стоимости этих доходов: она показывает, сколько денег могло бы получить предприятие, если бы разместило приведенную (сегодняшнюю) стоимость будущих поступлений на банковский депозит под 20%.
Дисконтирование денежного потока предполагает дисконтирование каждого его отдельного члена с последующим суммированием полученных результатов. Для этого используется дисконтный множитель математического дисконтирования по сложной процентной ставке i. Операции наращения и дисконтирования денежных потоков взаимообратимы, то есть наращенная сумма ренты может быть получена начислением процентов по соответственной сложной ставке i на современную (приведенную) величину этой же ренты (S = PV*; (1+i)n).
Таблица 2.3.2
Дисконтирование денежного потока
| № периода | 1 | 2 | 3 | 4 | 5 | Итого |
| 1.Член ренты, тыс. руб. | 3 | 3 | 3 | 3 | 3 | 15 |
| 2. Число лет от начальной даты | 1 | 2 | 3 | 4 | 5 | |
| 3.Множитель дисконтирования | 1/(1+0,2)1 | 1/(1+0,2)2 | 1/(1+0,2)3 | 1/(1+0,2)4 | 1/(1+0,2)5 | – |
| 4.Приведенная величина, тыс. руб. (стр.1*; стр.3) | 2,5 | 2,08 | 1,74 | 1,45 | 1,21 | 8,98 |
Из таблицы видно, что при альтернативных затратах 20% сегодняшняя стоимость будущих доходов составляет 8,98 тыс. руб. Именно эта величина и должна сравниваться с инвестициями для определения целесообразности принятия проекта или отказа от его реализации. Обобщая алгоритм, по которому выполнялись расчеты, получаем общую формулу дисконтирования денежных потоков:
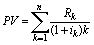 (3)
(3) Так как в нашем примере i и R постоянные величины, то, снова применяя правило суммирования геометрической прогрессии, получим частную формулу дисконтирования аннуитета:
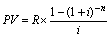 (4)
(4) Второй сомножитель этого выражения – (1 – (1 + i)-n) / i – называется дисконтным множителем аннуитета.
Кратко рассмотрим вечные ренты или перпетуитеты. Существуют финансовые инструменты, предполагающие бессрочную выплату доходов их держателям. Одним из примеров таких ценных бумаг являются т.н. консоли (консолидированные ренты), эмитируемые британским казначейством начиная с XVIII века. В случае смерти владельца они передаются по наследству, обеспечивая тем самым действительную “бесконечность” денежного потока. Очевидно, что будущую стоимость ренты такого рода определить невозможно – ее сумма также будет стремиться к бесконечности.
Лекция 8. Методы оценки финансовых активов
1. Основные виды ценных бумаг на фондовом рынке
2. Оценка акций и облигаций
1. Основные виды ценных бумаг на фондовом рынке
Акция - ценная бумага, свидетельствующая о внесении пая в капитал акционерного общества. Дает ее владельцу право на присвоение части прибыли в форме дивиденда.
Различают различные виды стоимости акций:
Нарицательная стоимость (номинал) - произвольная стоимость, устанавливаемая при эмиссии и отражаемая в акционерном сертификате. Номинал практически не связан с реальной стоимостью.
Балансовая стоимость, исчисляемая как частное от деления чистых активов корпорации на количество выпушенных и распространенных акций.
Рыночная стоимость ( продажная цена акции, курс ) - текущая стоимость акции на бирже или во внебиржевом обороте (к примеру, последняя котировка ). Это наиболее важный вид стоимости, поскольку именно она (а точнее - прогноз ее изменения ) играет основную роль в обращении акций данной корпорации.
Различают обыкновенные и привилегированные акции. Как и обыкновенные акции, привилегированные акции представляют собой ценную бумагу, указывающую на долю участия ее держателя в корпорации. От обыкновенных акций их отличает следующее:
- дивиденды на привилегированные акции, как правило, устанавливаются по фиксированной ставке;
- они выпускаются с указанием номинала и размера дивиденда в процентах или в долларах на акцию;
-дивиденды по привилегированным акциям выплачивается до выплат по обыкновенным акциям и не зависит от прибыли корпорации;
-держатели привилегированных акций имеют преимущественное право на определенную долю активов корпорации при ее ликвидации;
-как правило, держатели привилегированных акций не имеют преимущественных прав на покупку акций нового выпуска и права голоса.
Существуют следующие права, предоставляемые корпорацией своим акционерам:
1.Право голоса.
Большинство обыкновенных акций дает их держателю право голоса на ежегодных собраниях акционеров по всем важным вопросам деятельности корпорации (например, по изменениям в уставе корпорации, вопросам слияний и приобретений, финансовой реорганизации, выборам совета директоров компании). Так как большая часть акционеров не может (или не хочет) посещать собрания, корпорации обязаны оформлять доверенности, по которым акционеры передают совету директоров корпорации право голосовать от их имени на ежегодных или специальных собраниях. На биржах США оформление таких доверенностей является обязательным условием для регистрации компании и котировки ее ценных бумаг.
2. Право на участие в прибыли корпорации (на получение дивидендов).
Акции дают их держателям на получение части прибыли компании в форме дивидендов. Дивиденды - это часть прибыли корпорации, распределяемая среде акционеров в виде определенной доли от стоимости их акций (иначе говоря, пропорционально числу акций, находящихся в собственности). Дивиденды по обыкновенным акциям выплачиваются только после уплаты всех налогов, процентов по облигациям и дивидендов по привилегированным акциям (если такие выпущены).Обычно дивиденды выплачивают поквартально, но право решать здесь предоставлено совету директоров. По законодательству РФ корпорация вправе вообще не выплачивать дивиденды по простым акциям, хотя самой корпорации это не выгодно, так как подобные действия с высокой вероятностью негативно отразятся на курсе ее акций. По привилегированным акциям дивиденды компания выплатить обязана. Дивиденды выплачиваются наличными, в форме имущества и в форме акций самой корпорации.
3. Преимущественное право на покупку новых акций.
Право, дающее существующим акционерам возможность закупить акции нового выпуска прежде, чем они будут предложены другим лицам. Цель этого преимущественного права в защите существующих акционеров (в первую очередь держателей крупных пакетов) от "размывания" пропорциональных долей их участия в корпорации. Как правило в законодательстве предусматривается, что наличие таких прав должно прямо оговариваться в уставе корпорации.
При реализации таких прав акционер может закупить акции нового выпуска в размере, пропорциональном его фактической доле в капитале корпорации.
Эти права имеют определенную стоимость: цена подписки на новый выпуск акций обычно ниже рыночной цены уже выпущенных акций; в результате этого преимущественные права могут выступать объектом купли-продажи.
4. Право при ликвидации (роспуске) корпорации.
Ликвидация - это практические действия корпорации по прекращению дел и реализации имущества. Стадия прекращения легального существования называется роспуском, а фактического - ликвидацией. По закону РФ претензии к корпорации при ликвидации удовлетворяются ею в следующем порядке: государственные претензии (уплата налогов и пошлин, расчет по государственным кредитам), претензии других кредиторов (коммерческих банков, владельцев векселей и облигаций, и т.д.),претензии владельцев привилегированных акций, и только после этого претензии владельцев обыкновенных акций. Незнание этого положения (или непонимание того, что акционер является совладельцем корпорации) в нашей стране в последнее время приводит к конфликтам между учредителями и акционерами ликвидировавшихся корпораций.
5. Права на инспекцию (проверку).
Все акционеры имеют право на поверку некоторых документов и отчетностей своих корпораций (списка акционеров, протоколов собраний акционеров, некоторых бухгалтерских отчетов и тп.).
Облигация - (от латинского obligato - обязательство) ценная бумага на предъявителя, дающая владельцу право на получение годового дохода в виде фиксированного процента (в форме выигрышей и оплаты купонов).Облигация подлежит выкупу в течение обусловленного при выпуске займа срока.
В общем плане облигации представляют собой долгосрочные долговые обязательства с фиксированным процентом. Различают три основных категории облигаций: облигации корпораций, облигации федерального правительства (в том числе федеральных органов и учреждений) и муниципальные облигации.
Облигации корпораций - это обязательства корпораций перед кредиторами о выплате в установленные сроки суммы долга и процентов по полученным займам. Как и акции, облигации являются ценными бумагами, но в отличие от акций, которые представляют собой собственный капитал корпораций, облигации являются выразителями заемного капитала, то есть для корпорации они являются "долговыми бумагами". Держатели облигаций (облигационеры) являются кредиторами корпорации, в то время как акционеры - ее совладельцами. В связи с этим права облигационеров отличны от прав акционеров: они не имеют права голоса и не могут участвовать в управлении компанией-эмитентом, но в то же время она обязана выплачивать проценты по облигациям (в отличие от дивиденда по акциям, где никаких подобных обязательств у корпорации нет), причем делать это до рассмотрения вопроса о дивидендах по акциям. Кроме того, при ликвидации компании облигационеры имеют преимущественные права по сравнению с акционерами.
Облигационные отношения оформляются специальным договором между фирмой-эмитентом и инвестором (облигационным соглашением), по условиям которого корпорация обязуется возместить инвестору предоставленную им сумму в установленный срок ("срок погашения" или "дата погашения"), а также в течение всего срока, на который выпущена облигация, выплачивать проценты по установленной ставке. Как и акционер, облигационер получает соответствующий документ, подтверждающий факт его владения облигациями, - облигационный сертификат, в котором указываются название компании-эмитента, номинал, ставка процента, а также имя/название "платежного агента" как по процентам, так и по капитальной сумме облигации (таким агентом может быть сама фирма-эмитент или какой-либо банк).
Виды облигаций:
1. Купонные облигации или облигации на предъявителя.
К ним прилагаются специальные купоны, которые должны откалываться два раза в год и представляться платежному агенту для выплаты процентов. Фактически купон - своеобразный простой вексель на предъявителя. Эти облигации обратимы, а купон и сертификат выступают в качестве титула собственности. Поскольку эти облигации оформляются на предъявителя, корпорация не регистрирует, кто является их собственником. Хотя они больше не выпускаются, старые выпуски все еще обращаются на рынке
2. Именные облигации.
Большинство облигаций корпораций регистрируются на имя их владельца, при этом ему выдается именной сертификат. Эти облигации не имеют купонов, а платежи по процентам осуществляет платежный агент в соответствии с установленным графиком. При продаже или обмене именных облигаций старый сертификат аннулируется и выпускается новый - с указанием нового владельца облигаций.
3. "Балансовые" облигации.
Этот вид облигаций приобретает все большее распространение, поскольку их выпуске не сопряжен с такими формальностями, как выдача сертификатов и т.п.: просто все необходимые данные об облигационере вводятся в компьютер.
В зависимости от обеспечения облигации разделяются на:
1. Обеспеченные облигации. Эти облигации имеют реальное обеспечение активами. Их можно разбить на три подтипа:
a) облигации с залогом имущества, которые обеспечиваются основным капиталом корпорации (ее недвижимостью) и иным вещным имуществом;
b) облигации с залогом фондовых бумаг, которые обеспечиваются находящимися в собственности компании-эмитента ценными бумагами какой-либо другой корпорации (но не компании-эмитента) - как правило, ее филиала или дочерней компании;
с) облигации с залогом оборудования. Такие облигации обычно выпускаются транспортными корпорациями, которые в качестве залогового обеспечения используют, например, транспортные средства (самолеты, локомотивы и т.п.).
Смысл залогового обеспечения заключается в том, что в случае банкротства компании или ее неплатежеспособности держатели обеспеченных облигаций могут претендовать на часть имущества компании.
2. Необеспеченные облигации. Эти облигации не обеспечиваются какими-либо материальными активами, они подкрепляются добросовестностью компании-эмитента, иначе говоря - ее обещанием. В случае банкротства компании держатели таких облигаций не могут претендовать на часть недвижимости. Эти облигации менее надежны, но и на них распространяются преимущественные права при ликвидации компании. В связи с тем же ставка процента по ним более высокая.
3. Другие виды облигаций.
a) Облигации с доходом на прибыль, или реорганиза-ционные облигации предусматривают выплату процентов только в том случае, если у корпорации имеются существенные поступления, то есть в случае выпуска таких облигаций гарантируется погашение ее основной суммы, а выплата процентов зависит от решения совета директоров. Выпуск таких облигаций практикуется при рекапитализации корпорации - как правило, когда ей грозит банкротство.
b) Гарантированные облигации: они гарантируются не корпорацией-эмитентом, а другими компаниями. Чаще всего они используются: транспортными корпорациями, когда эмитент предоставляет какой-либо компании свое оборудование, а взамен эта компания выступает гарантом по облигациям первой фирмы, либо дочерними компаниями крупных фирм, когда дочерняя компания выпускает облигации, а гарантом выступает основное предприятие. Как видно из названия, в случае неплатежеспособности эмитента, все претензии облигационеров удовлетворяются гарантом.
c) Бескупонные облигации. По ним не выплачивается регулярного процента, однако это не значит, что они не при носят дохода. Дело в том, что при выпуске эти облигации продаются с диконтом ( со скидкой ), а погашаются по номинальной цене при наступлении срока платежа, причем скидка тем больше, чем длиннее срок, на который выпущены облигации.
Стоит отметить, что в современной практике различия между акциями и облигациями корпораций постепенно стираются. С одной стороны, происходит узаконивание выпуска "не голосующих" акций, а с другой - появились "голосующие" облигации. Стиранию этих различий также способствует так же эмиссия конвертируемых облигаций и выпуск так называемых "гибридных фондовых бумаг". Это явление отражает в определенной мере тенденцию сращивания промышленного и банковского капитала.
2. Оценка акций и облигаций.
Стоимость прив акции – текущая стоимость в ден выражении серий равных периодических потоков ден средств (дивидендов), имеющих место без ограничения во времени. Т.к. дивиденды для каждого временного периода остаются неизменными, модель оценки имеет следующий вид:
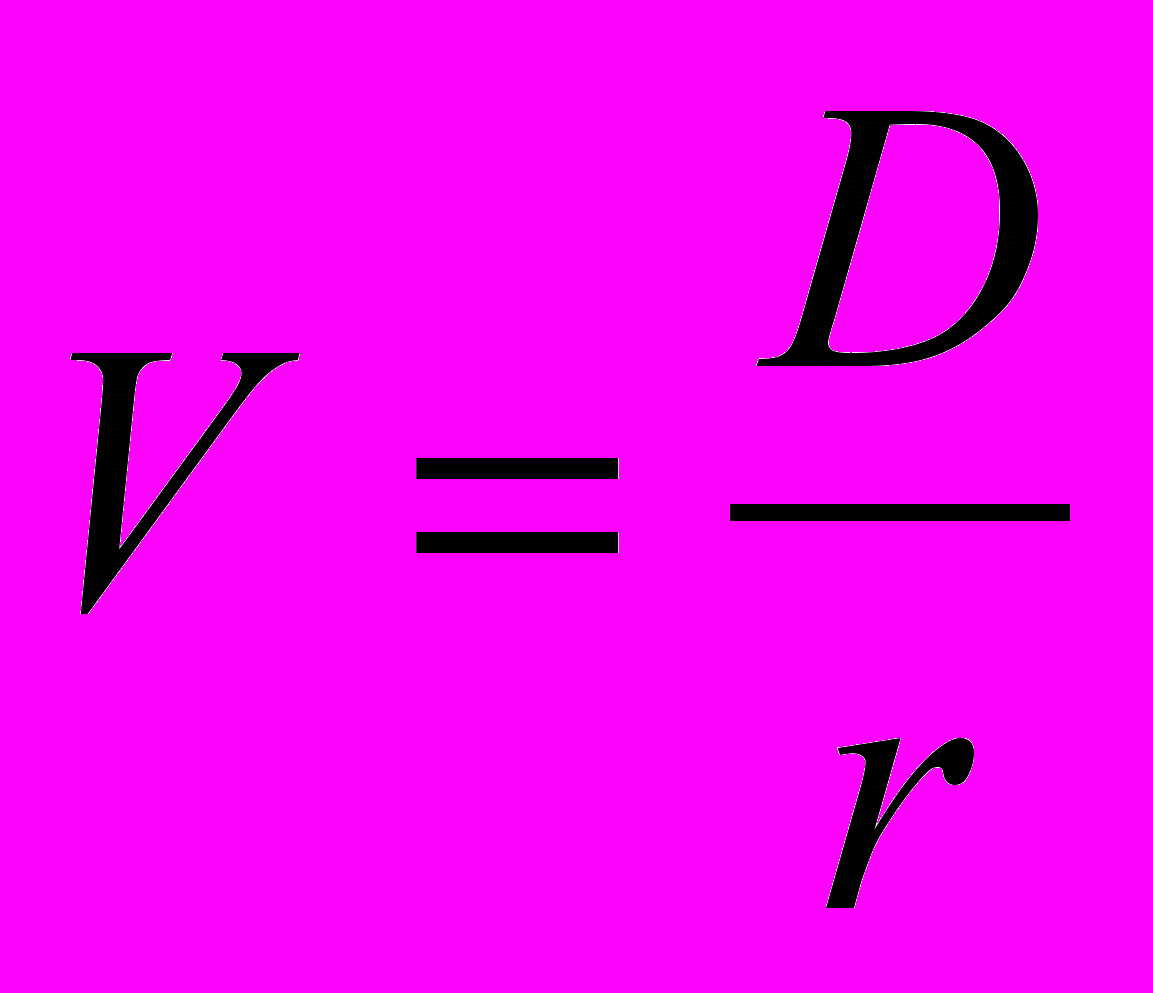 где V – текущая стоимость прив акции; D – годовой дивиденд, r – требуемая ставка дохода инвестора.
где V – текущая стоимость прив акции; D – годовой дивиденд, r – требуемая ставка дохода инвестора.Стоимость обыкн акции представляет собой текущую стоимость всех будущих притоков ден средств, ожидаемых инвестором, включая дивиденды и будущую стоимость на дату ее продажи.
Для инвестора, владеющего обыкн акцией в течение только одного года, стоимость акции:
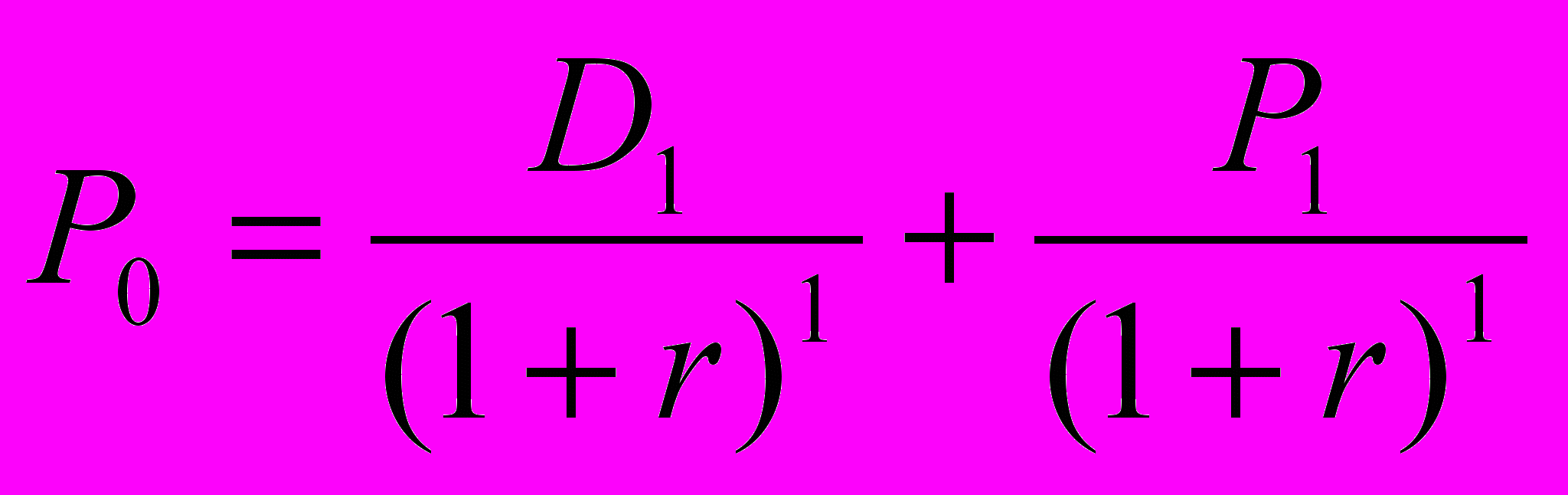 где D1-дивиденды за 1 год; Р1-рыночная стоимость на конец года.
где D1-дивиденды за 1 год; Р1-рыночная стоимость на конец года.Для многократного периода владения модель оценки обыкн акции:
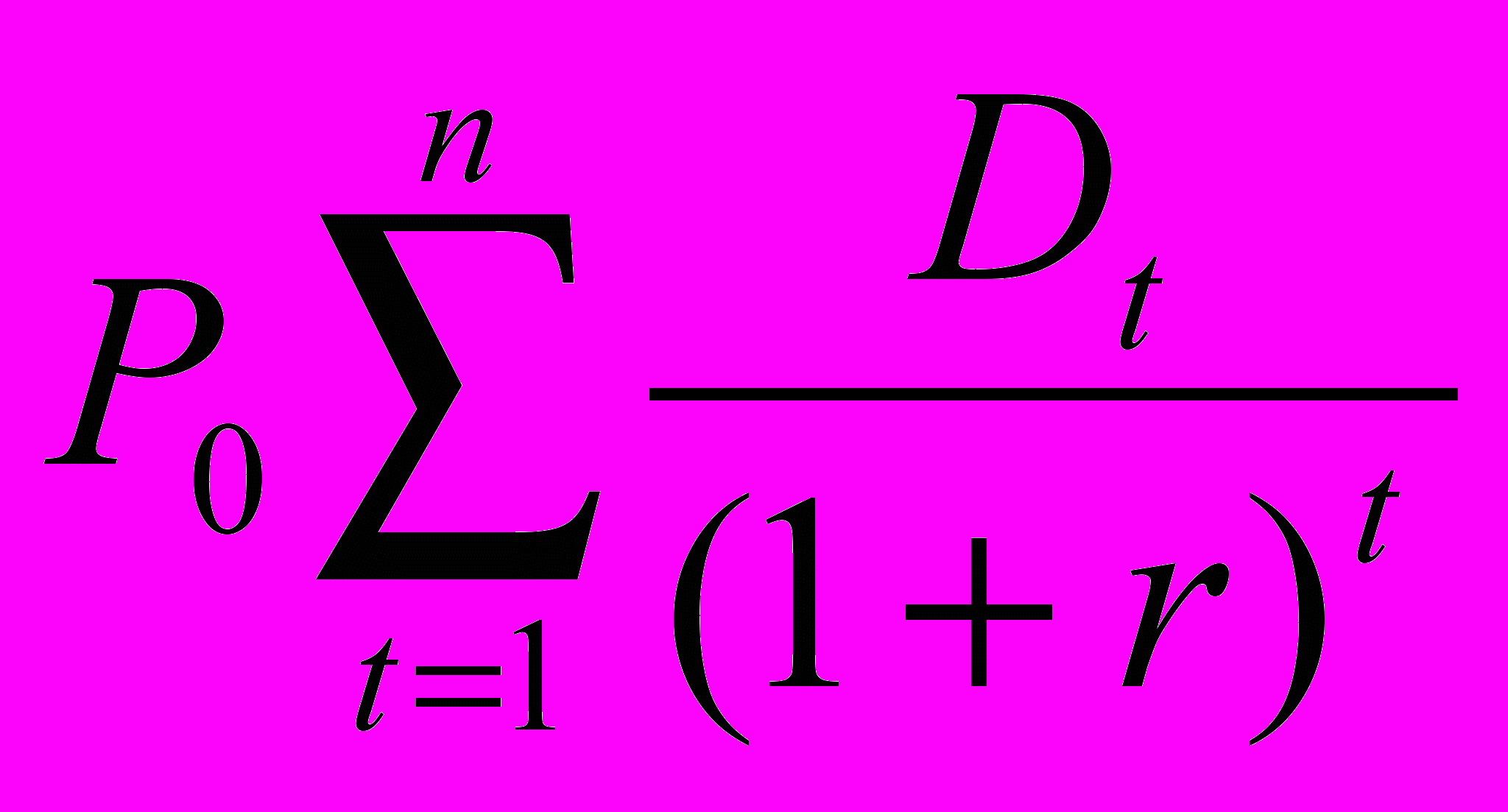 где Dt-дивиденды за период t от 1 до n лет
где Dt-дивиденды за период t от 1 до n лет Дивиденды могут быть разделены по категориям: дивиденды с нулевым ростом и дивиденды с постоянным ростом.
В случае нулевого роста (D0=D1=…D) модель оценки стоимости акций будет иметь вид:
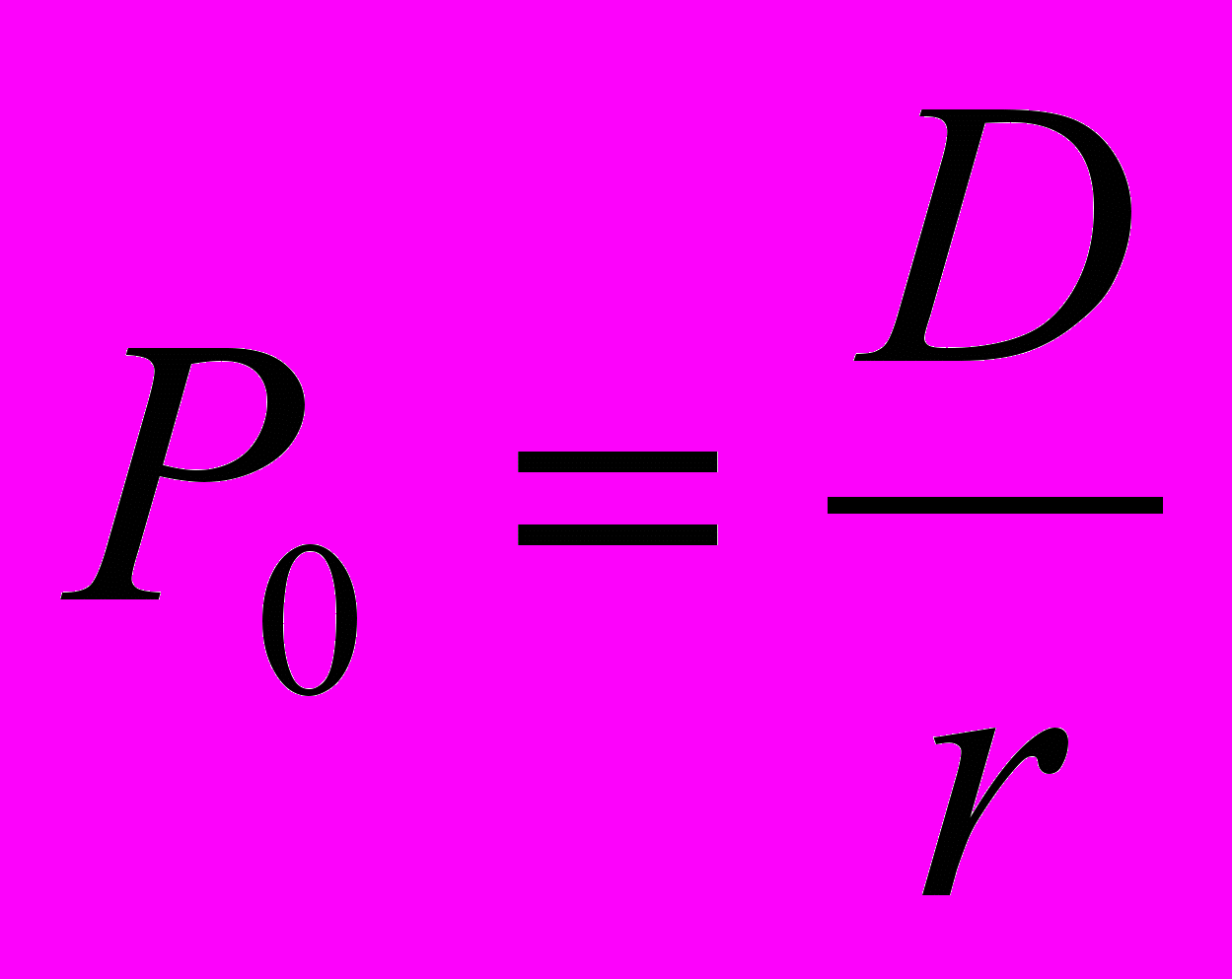
В случае постоянного роста, если мы предположим, что дивиденды растут с постоянным темпом g в год:
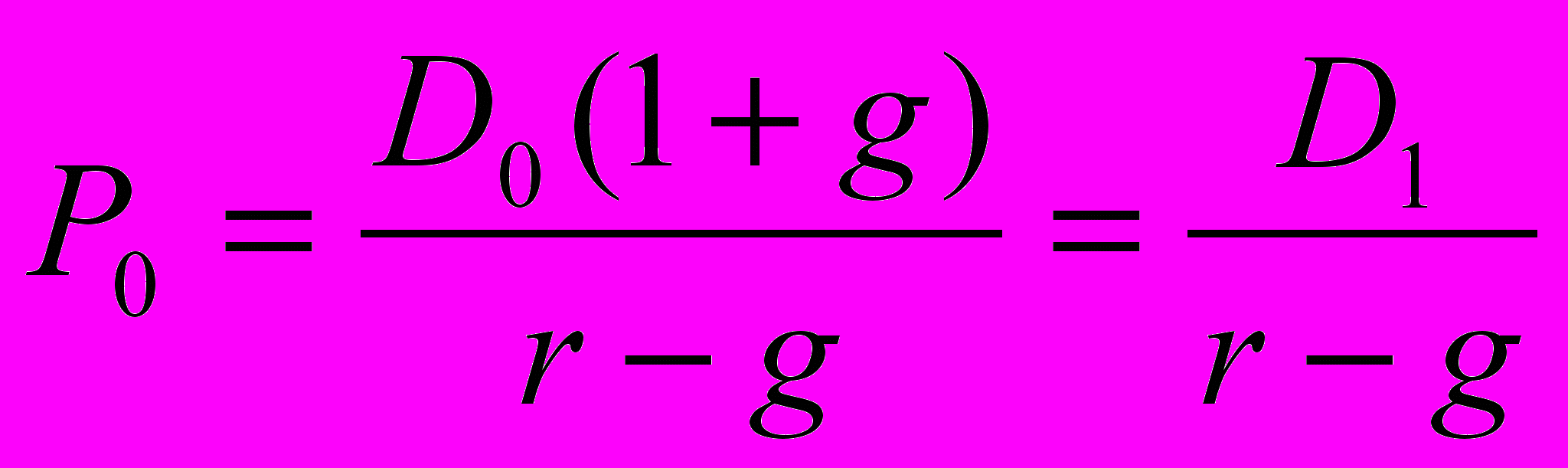 - это модель Гордона.
- это модель Гордона.Оценка текущей стоимости акций определяется по следующей формуле:
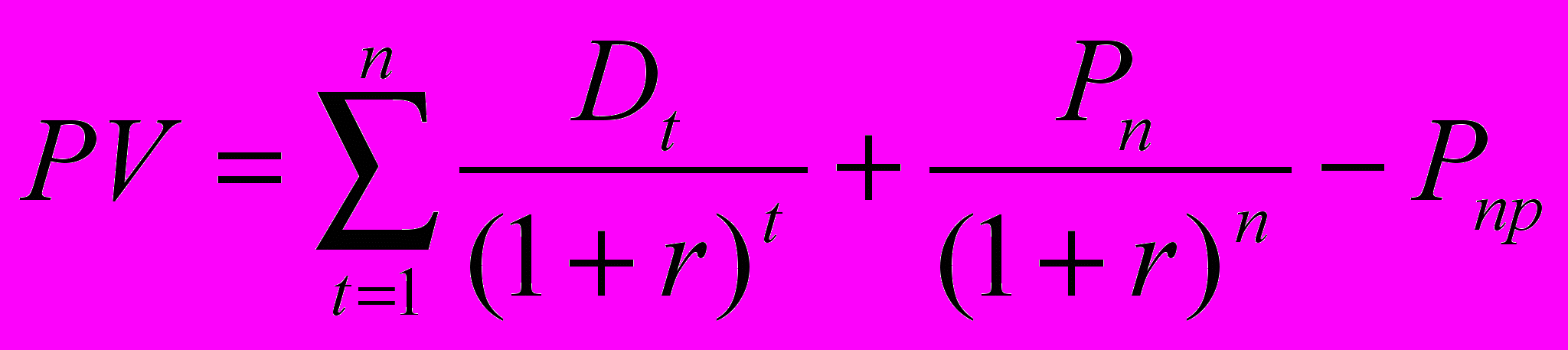 где Pп – цена продажи акции через n периодов, Pпр – цена приобретения акции на текущий период времени.
где Pп – цена продажи акции через n периодов, Pпр – цена приобретения акции на текущий период времени.Оценка облигаций с нулевым купоном:
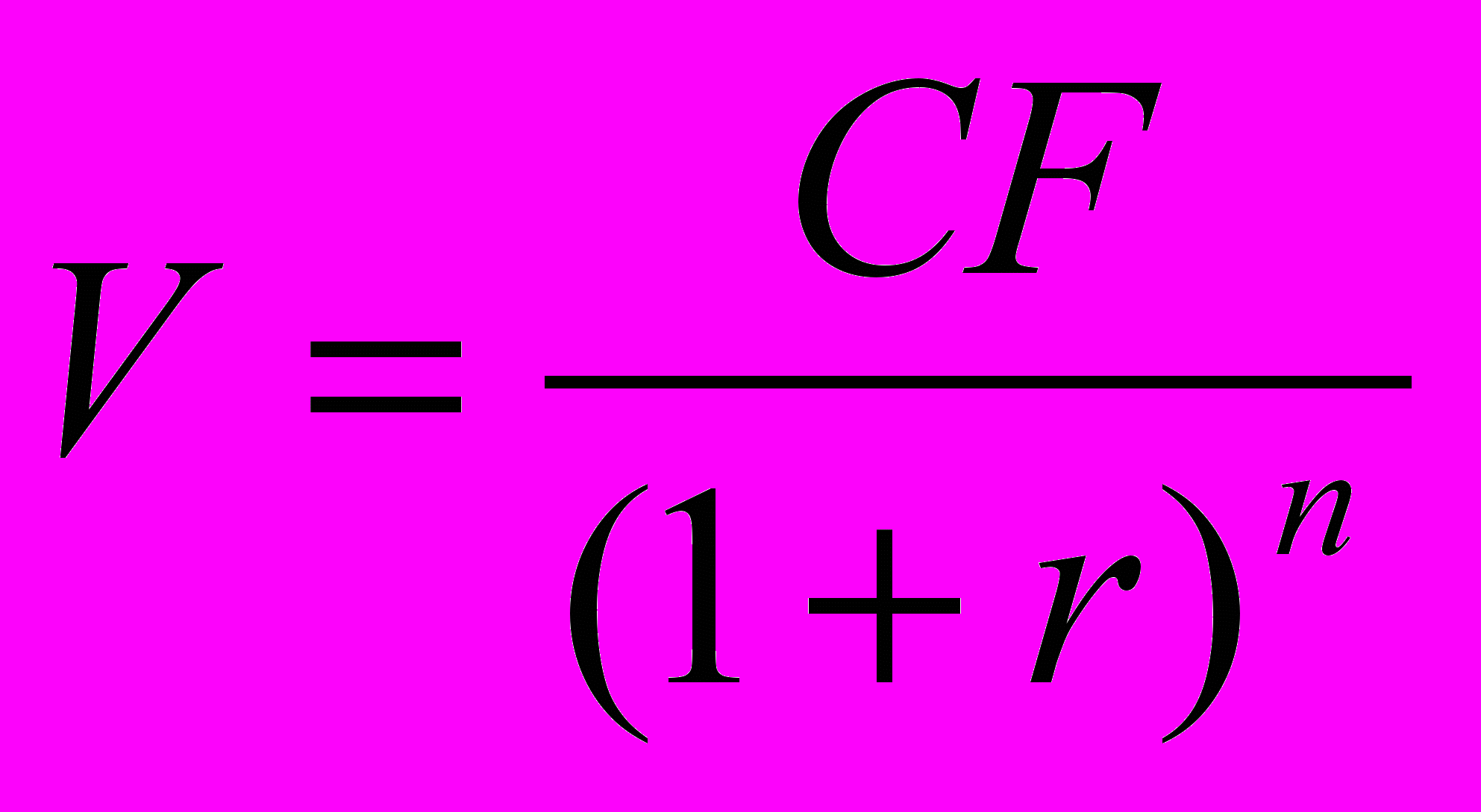 где V – стоимость облигации с позиции инвестора, CF-сумма, выплачиваемая при погашении облигации, n- срок обращения, в годах, r – доходность на рынке за этот же период.
где V – стоимость облигации с позиции инвестора, CF-сумма, выплачиваемая при погашении облигации, n- срок обращения, в годах, r – доходность на рынке за этот же период.Если облигация бессрочная, то Vt=CF/r CF-сумма, выплачиваемая за период.
Доходность облигации без права досрочного погашения:
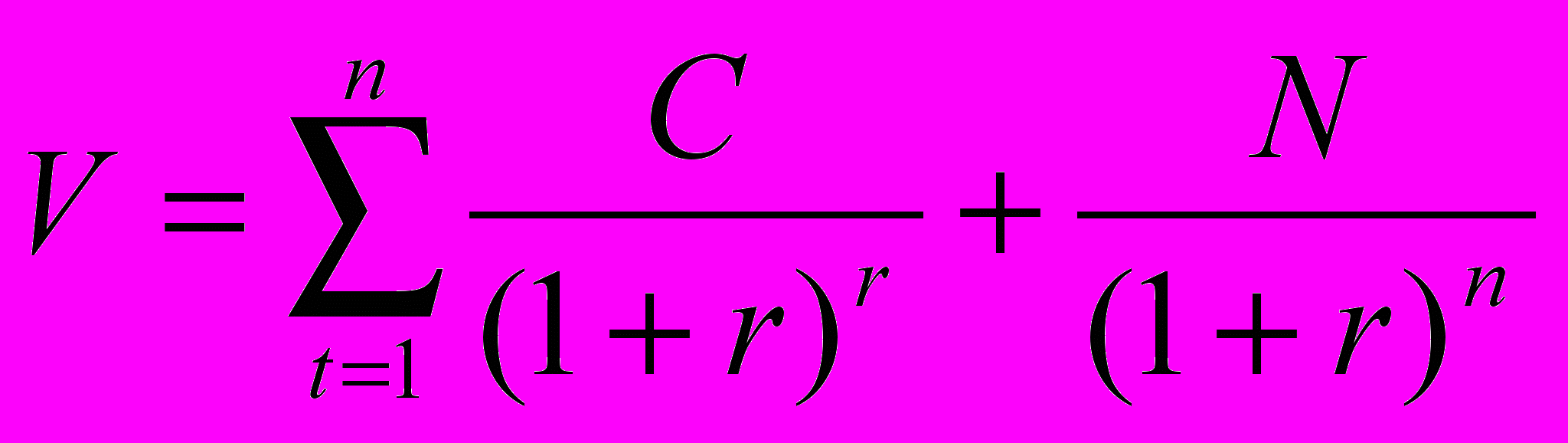 где r-доходность требуемая инвестором, С – купонный период, N – номинал облигации, n – количество лет до срока погашения
где r-доходность требуемая инвестором, С – купонный период, N – номинал облигации, n – количество лет до срока погашения