Рабочая программа
| Вид материала | Рабочая программа |
Содержание4.8. “Построения геометрических фигур” Итог задача имеет единственное решение. б I. Анализ |
- Рабочая программа по дисциплине: Экономика недвижимости для специальности: Экспертиза, 293.4kb.
- Рабочая программа по дисциплине: Теоретические основы оценки собственности для специальности:, 226.61kb.
- Рабочая программа по дисциплине: Экономика недвижимости для специальности: Экономика, 293.45kb.
- Рабочая программа По истории 10 класс Пояснительная записка, 116.13kb.
- Рабочая программа учебной дисциплины ф тпу 1 -21/01, 102.93kb.
- Рабочая программа учебной дисциплины ф тпу 1-21/01 утверждаю, 68.83kb.
- Рабочая программа Программа лекционного курса План практических занятий, 1059.44kb.
- Рабочая программа Программа лекционного курса План практических занятий, 825.14kb.
- М. К. Аммосова программа к урса строение вещества для государственных университетов, 197.97kb.
- Рабочая программа по дисциплине «разработка и управление социальными проектами и программами», 92.78kb.
4.8. “Построения геометрических фигур”
Для подготовки: рассмотрите № 4 ( с решением).
Примерные задачи №№ 1 – 46.
- Провести общую касательную к двум окружностям.
- Построить зная его сторону, биссектрису, проведенную к этой стороне и точку пересечения этой биссектрисы с данной стороной.
- Построить три окружности, попарно касающихся друг друга внешним образом, чтобы их центры являлись вершинами данного треугольника.
- Построить окружность, проходящую через две данные точки и касающуюся данной прямой.
- Разделить угол и отрезок пополам, пользуясь двусторонней линейкой.
- Построить по двум углам и периметру.
- Построить по высоте и медиане, проведенным к данной стороне.
- Построить по трем медианам.
- Построить по углу, прилежащей к нему стороне и разности двух других сторон.
- Построить равнобедренный по боковой стороне и сумме основания и высоты.
- Через данную точку к данной окружности провести секущую, чтобы ее внешняя часть была вдвое больше внутренней.
- Построить ромб, зная его диагональ и радиус вписанной окружности.
- Построить квадрат ABCD так, чтобы А и В принадлежали данной окружности, а C и D – данной прямой.
- Построить параллелограмм так, чтобы его сторона и две высоты были равны данным отрезкам a, b и с.
- Построить окружность, касающуюся данной окружности и прямой q в данной точке А.
- Построить окружность, касающуюся данной окружности в данной на ней точке В и данной прямой.
- Постройте треугольник по заданным элементам: а) a, b, h; б) А, hb, ha; в) А, b + с, hb; г) А, a, b–с; д) А, В, Р, где Р = а + b + с; е) а, ma А + В; ж) В, А, а; з) a, b + с, hс .
- Постройте треугольник по стороне, биссектрисе к ней и точке пересечения биссектрисы со стороной.
- Найдите множество точек:
а) равноудаленных от двух параллельных прямых;
б) от двух пересекающихся прямых;
в) середин всех равных хорд, проведенных в данной окружности.
- Найти множество точек Х, таких что:
а) АХ ВХ СХ, где АВС треугольник;
б) касательные, проведенные из точки Х к данной окружности имеют данную длину.
- На окружности зафиксирована точка А. Найти множество точек Х, делящих хорды с концом в точке А в отношении 1:2, считая от точки А.
- Из данной точки, лежащей вне круга, провести секущую так, чтобы ее внешняя часть а) равнялась внутренней; б) была втрое больше внутренней.
- Постройте треугольник, у которого один катет вдвое больше другого, а сумма катетов и высоты, опущенной на гипотенузу равна данному отрезку.
- (С решением.) В данный АВС вписать прямоугольный равнобедренный MNP, где М – вершина прямого угла на стороне АВ.
а) М задана на отрезке АВ; б) М не задана.
Рассуждать можно так:
а) I. Анализ (чертеж 3)
Чтобы построить MPN достаточно построить P и N на сторонах АС и ВС.
MP=MN P и N лежат на окружности с центром в М. Учитывая свойства поворота вокруг точки можно получить N=R
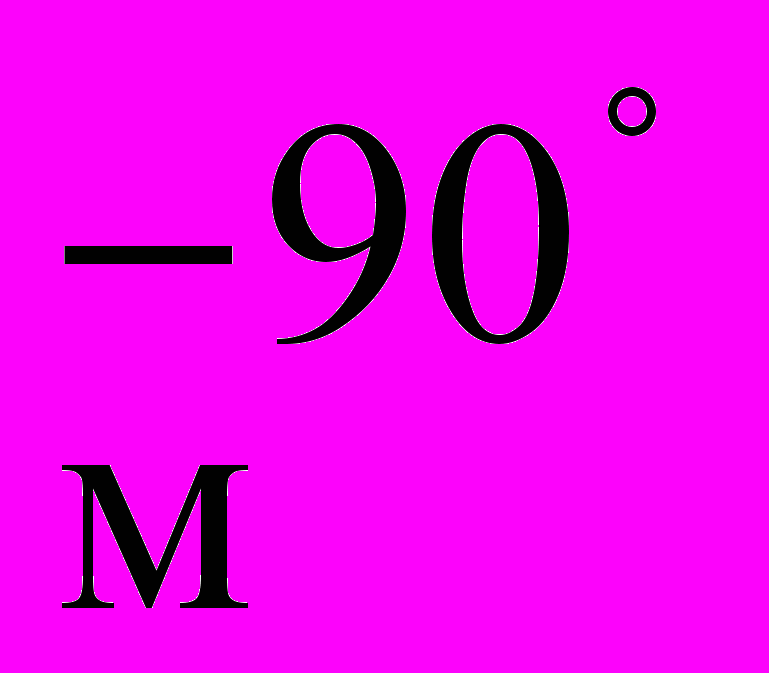 (P) N = BC AB,
(P) N = BC AB, где ВС= R
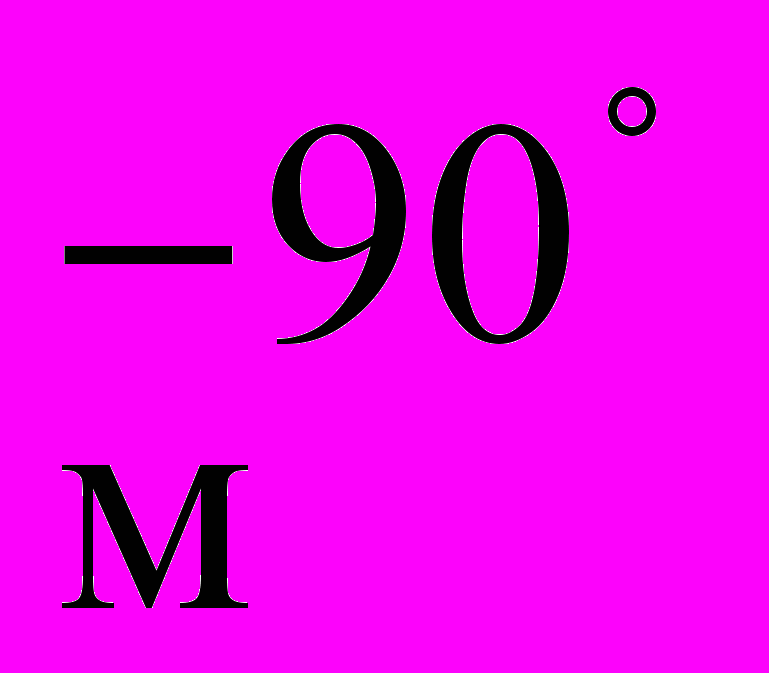 (ВС).
(ВС).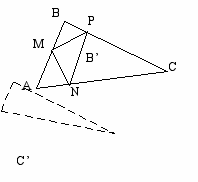
чертеж 3
II. Построение: (план)
- R
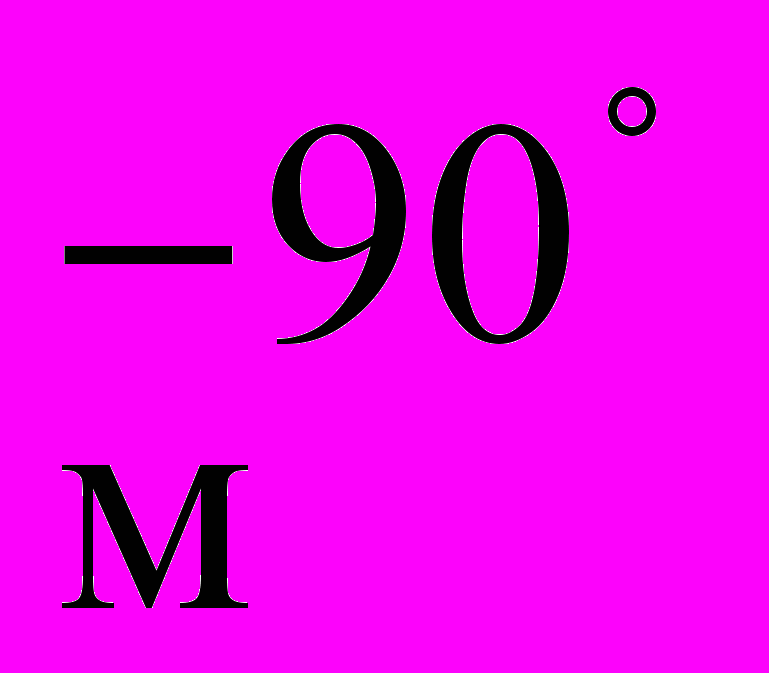 (ВС) = В С
(ВС) = В С
- N = ВС АС
- Р = R
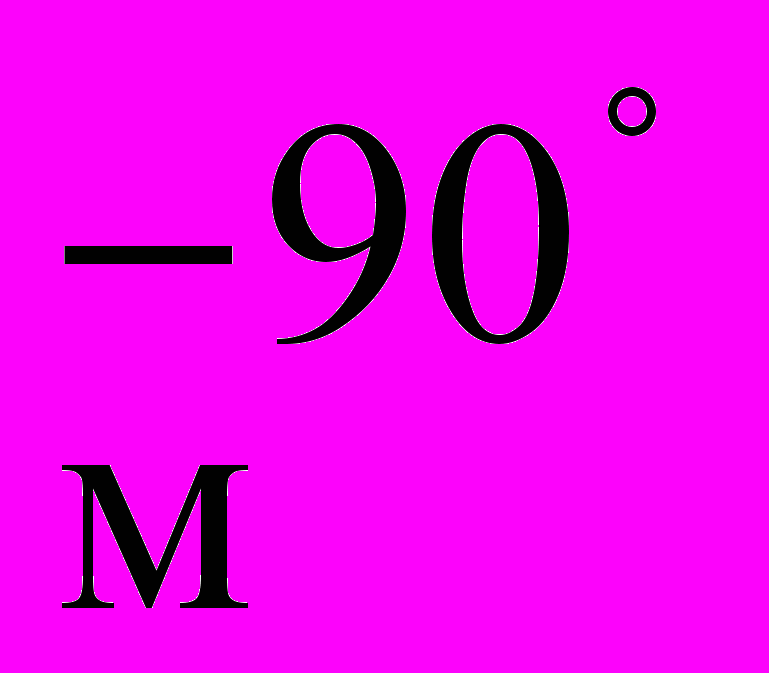 (N) (можно так: 3) РВ = ВN или 3) Р = ВС окр. (М, r = MN)) PMN – искомый.
(N) (можно так: 3) РВ = ВN или 3) Р = ВС окр. (М, r = MN)) PMN – искомый.
III. Доказательство:
Докажем: 1) что MPN – вписанный в АВС, т.е. М, Р и N лежат на сторонах АВС. (по построению).
2) NMP = 90 (угол поворота, т.к. Р и N соответствующие друг другу точки, М – неподвижная точка – центр поворота).
3) МР = MN (как отрезки, соединяющие образ и прообраз с центром поворота М).
Следовательно, треугольник удовлетворяет всем требованиям задачи.
IV. Исследование (проводим по этапам построения)
1. Образ отрезка ВС при повороте вокруг любой точки на любой угол можно получить всегда, причем единственный.
2. Пересечение двух отрезков единственная точка, если существует. Выясним когда ВС и АС не пересекутся? (чертеж 4).
АС ВС = , если МВ МЕ. В этом случае МЕР (Е N) можно считать вписанным в АВС (см. Определение вписанных фигур “Математическая энциклопедия”). Только 2 вершины М и Р лежат на АВ, но это не противоречит условию задачи.
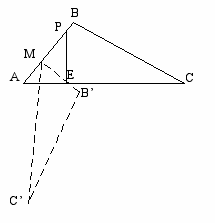
чертеж 4
3. Если существует N, то Р существует и единственно.
Итог задача имеет единственное решение.
б I. Анализ: (чертеж 5)
В MPN не дано ни одной точки, тогда можно построить любой равнобедренный прямоугольный треугольник МРN (или квадрат МРNK), чтобы М, N можно получить из М, N как образ при гомотетии с центром А и
 , где Р=АР ВС.
, где Р=АР ВС.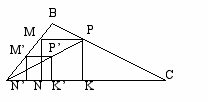
чертеж 5
II. Построение:
- Любой треугольник МРN, чтобы МР = М N, М АВ, N АС.
- Луч МР ВС =Р,
 .
.
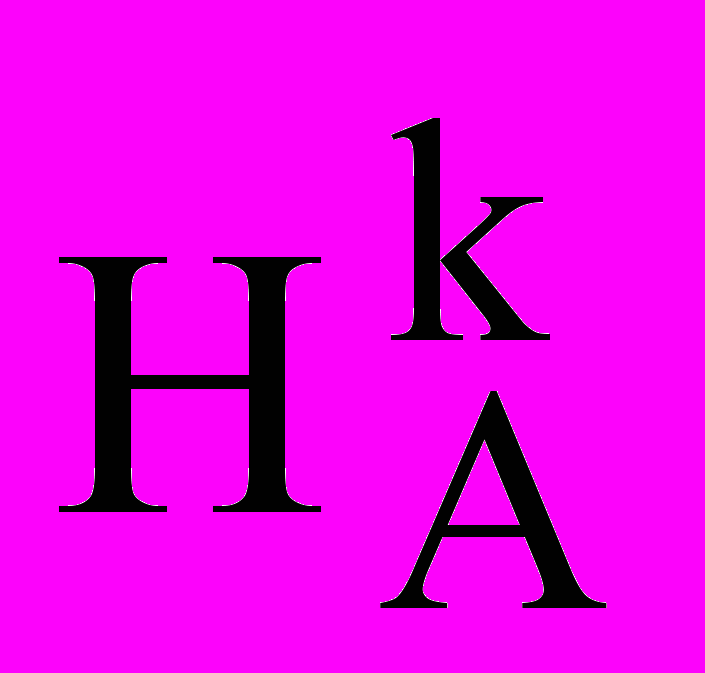 ( МРN) = MPN- искомый. (эдесь как половина квадрата) чертеж 5.
( МРN) = MPN- искомый. (эдесь как половина квадрата) чертеж 5.
III. Доказательство:
- Точки М, Р и N лежат на сторонах АВС по построению.
- МР = MN, т.к. МР = М N по построению.
- М = М = 90 (при гомотетии сохраняются углы без изменения) и т.д.
IV. Исследование:
1. Так как MPN строим произвольный, то таких треугольников может быть несколько, удовлетворяющих требованиям задачи, тогда и образов получится несколько (зависит от угла АМN) т.е. задача имеет множество решений, т.к. полученные образы будут иметь разные катеты.
Рассмотрите решение задачи. Решите аналогичную задачу, если нужно вписать правильный MPN.
- (задача об удвоении квадрата). Постройте квадрат, площадь которого вдвое площади данного квадрата.
- Постройте квадрат, площадь которого равна сумме площадей двух данных прямоугольников.
- В данную окружность вписать треугольник, если даны точки пересечения продолжения его биссектрис с окружностью.
Приложение 8
Коллоквиум
