Рабочая программа
| Вид материала | Рабочая программа |
- Рабочая программа по дисциплине: Экономика недвижимости для специальности: Экспертиза, 293.4kb.
- Рабочая программа по дисциплине: Теоретические основы оценки собственности для специальности:, 226.61kb.
- Рабочая программа по дисциплине: Экономика недвижимости для специальности: Экономика, 293.45kb.
- Рабочая программа По истории 10 класс Пояснительная записка, 116.13kb.
- Рабочая программа учебной дисциплины ф тпу 1 -21/01, 102.93kb.
- Рабочая программа учебной дисциплины ф тпу 1-21/01 утверждаю, 68.83kb.
- Рабочая программа Программа лекционного курса План практических занятий, 1059.44kb.
- Рабочая программа Программа лекционного курса План практических занятий, 825.14kb.
- М. К. Аммосова программа к урса строение вещества для государственных университетов, 197.97kb.
- Рабочая программа по дисциплине «разработка и управление социальными проектами и программами», 92.78kb.
4.4. Лист опроса № 2 (30 вопросов)
- Свойства точек и прямой.
- Свойства измерения отрезков.
- Свойства измерения углов.
- Свойства измерения площади.
- Свойства откладывания угла.
- Свойства откладывания отрезка.
- Свойства биссектрисы угла.
- Свойства серединного перпендикуляра к отрезку.
- Свойство точки пересечения медиан треугольника.
- Признаки равенства треугольников.
- Признаки равенства прямоугольных треугольников.
- Признаки подобия треугольников.
- Отношение периметров подобных фигур.
- Отношение площадей подобных фигур.
- Признаки параллельности прямых.
- Свойство углов при параллельных прямых и секущей.
- Свойства параллелограмма.
- Признаки параллелограмма.
- Свойства равнобедренного треугольника.
- Свойства ромба.
- Свойства прямоугольника.
- Неравенства треугольника.
- Свойства биссектрисы треугольника.
- Свойства медианы треугольника.
- Свойства средней линии треугольника.
- Свойства средней линии трапеции.
- Свойство четырехугольника, вписанного в окружность (описанного около …).
- Свойство смежных углов.
- Свойство вертикальных углов.
- Свойства внешнего угла треугольника.
Приложение 5
4.5. Лист опроса № 3
Элементарные задачи на построение циркулем и линейкой.
- Деление отрезка пополам.
- Деление угла пополам.
- Построение отрезка равного данному.
- Построение угла равного данному.
- Проведение перпендикуляра к прямой из точки на прямой.
- Проведение перпендикуляра к прямой из точки вне прямой.
- Построение треугольника по определяющим его элементам (ССС, СУС, УСУ).
- Деление отрезка в данном отношении.
- Построение касательной к данной окружности из данной вне ее точки.
- Построение общей внешней касательной к 2-м окружностям .
- Построение внутренней касательной к 2-м окружностям.
- Множество точек, лежащих на данном расстоянии от данной прямой.
- Множество точек, равноудаленных от сторон угла.
- Множество точек, равноудаленных от 2-х данных точек.
- Множество точек, из которых данный отрезок виден под данным углом.
- Множество точек, середин хорд данной окружности, проходящих через данную точку.
- Множество точек, для которых разность квадратов расстояний до 2-х данных точек есть постоянная величина.
- Множество точек, отношение расстояний до 2-х данных точек есть величина постоянная, отличная от 1.
- Построение х по формулам, где а, b, с – отрезки, m, n - числа натуральные:
а) х = а + b г)
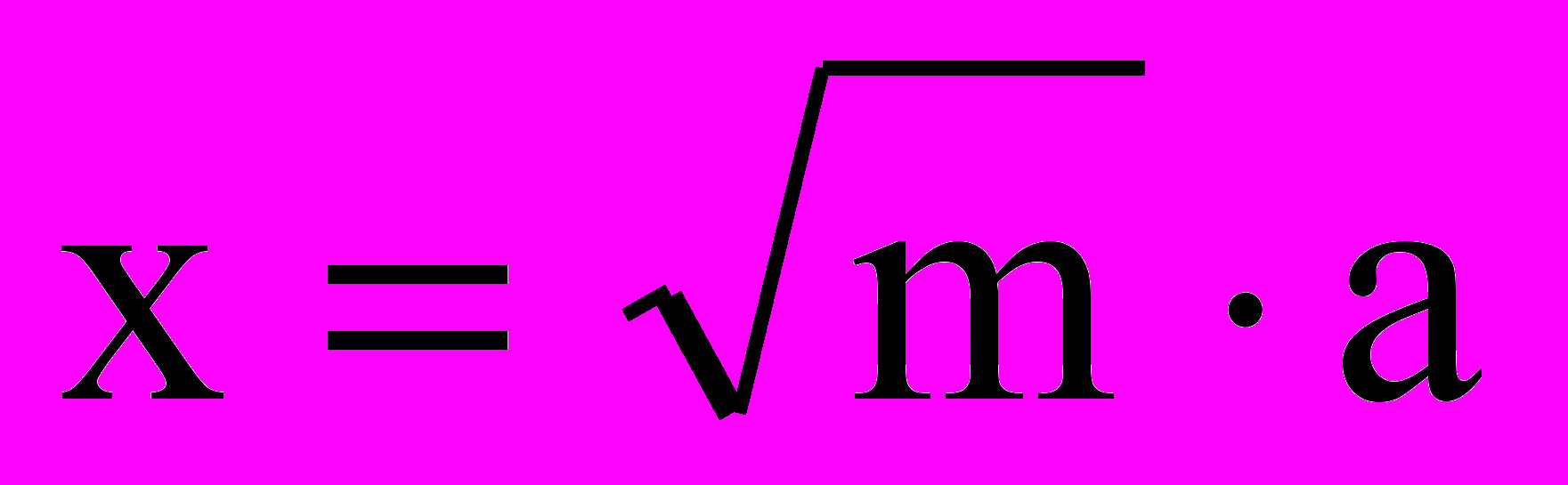 ж)
ж) 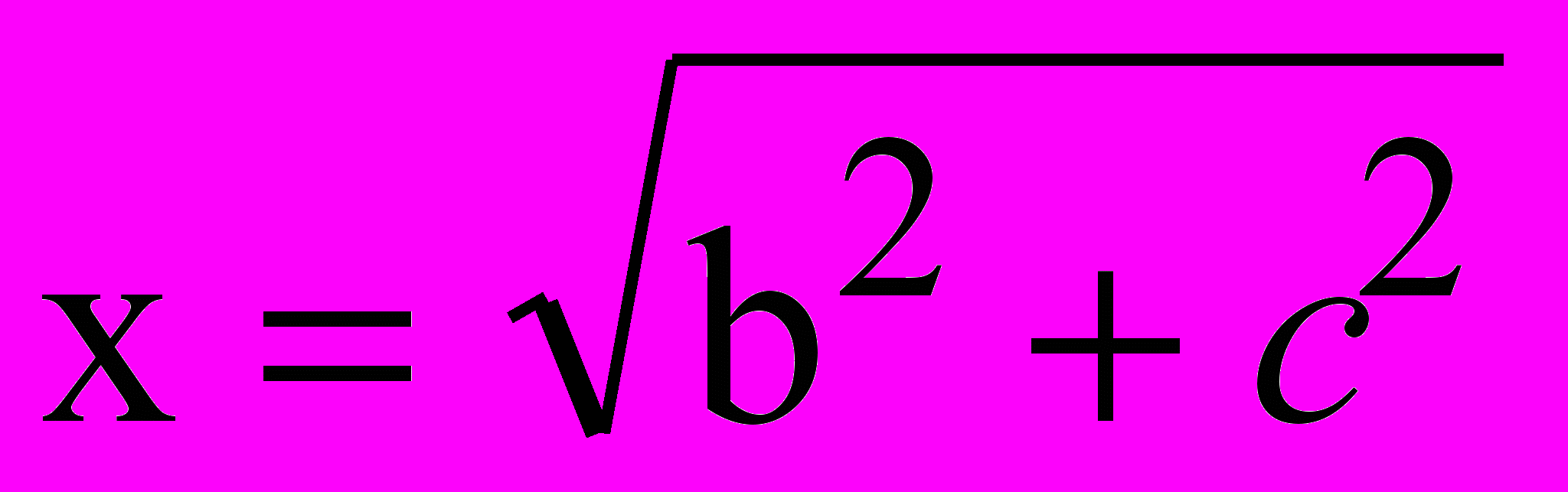 к)
к) 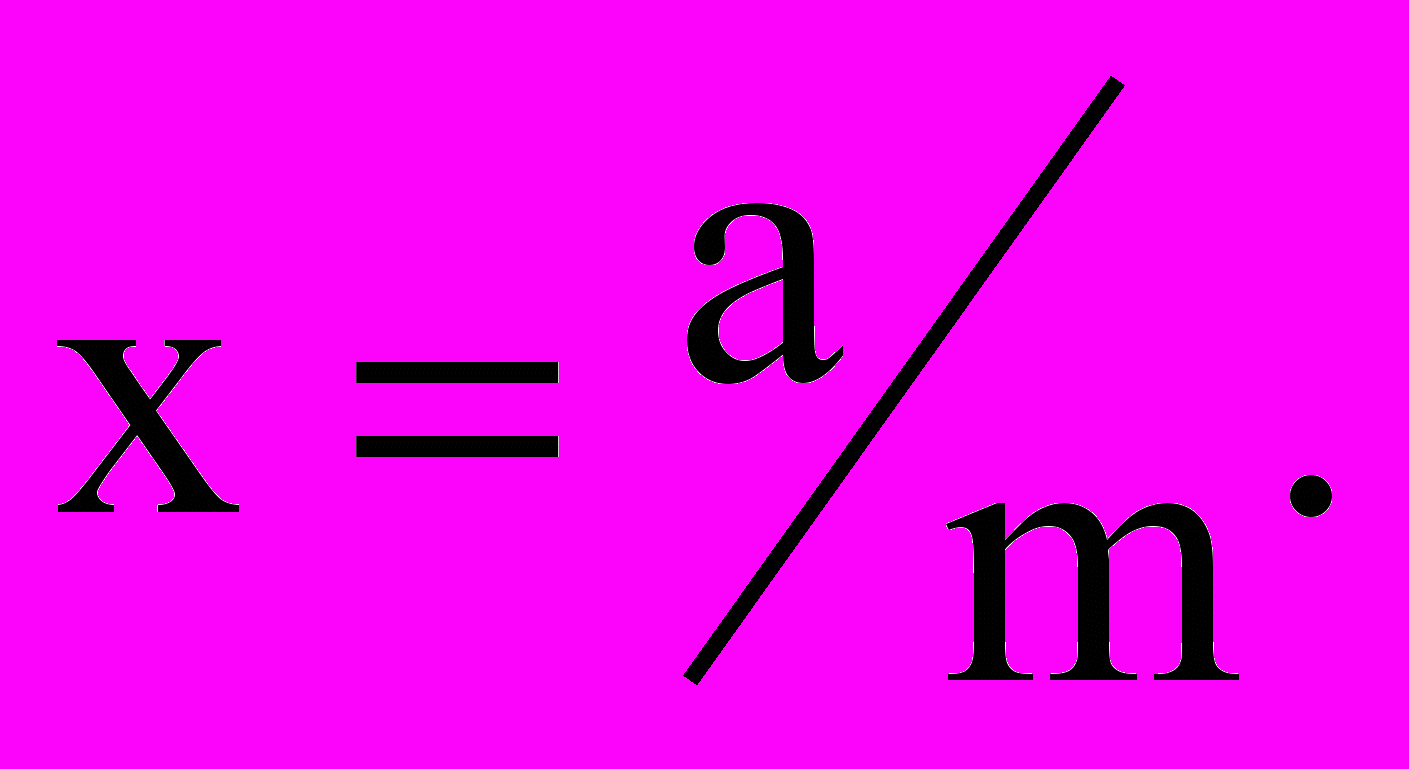
б) х = а – b д)
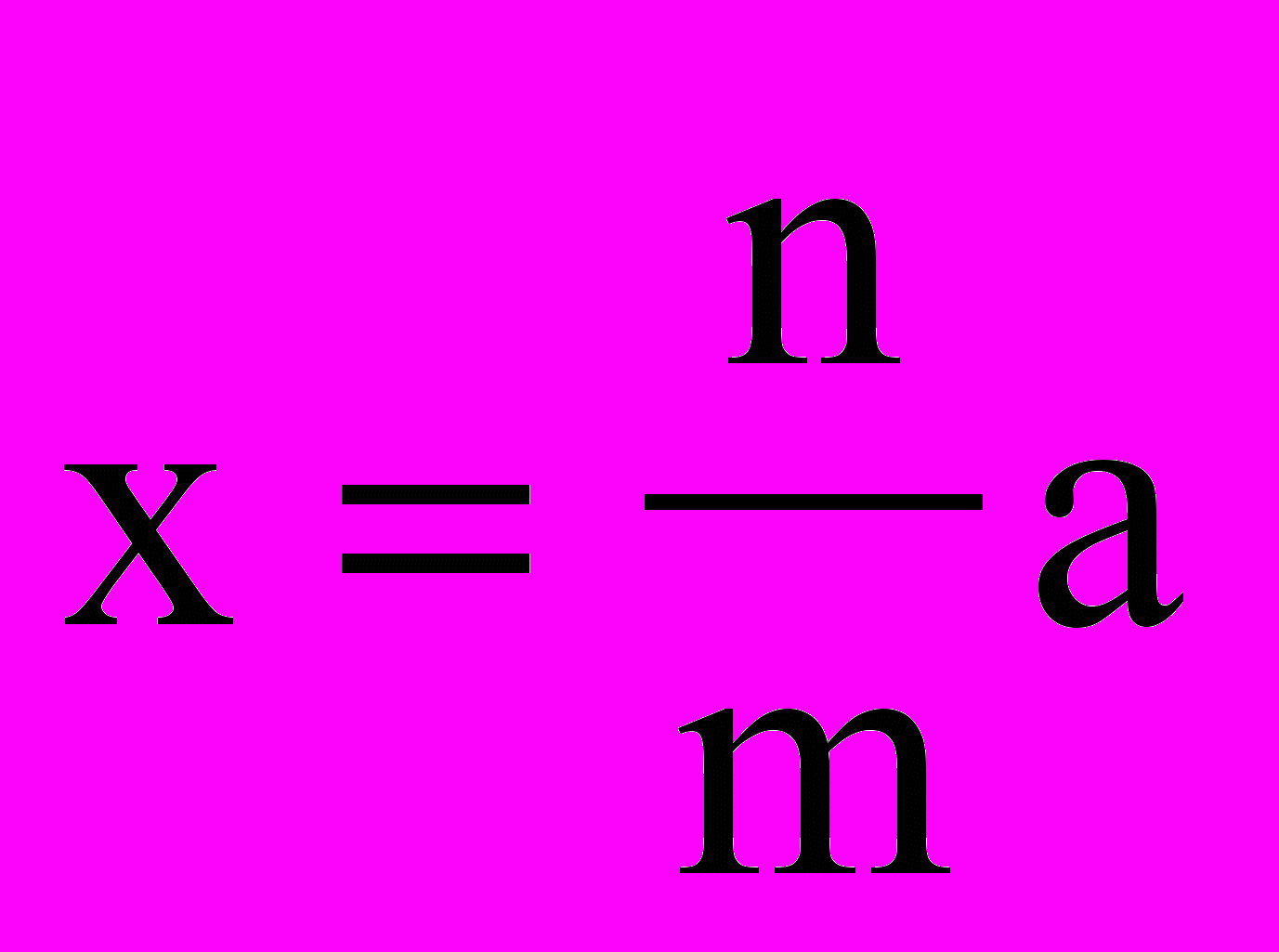 з)
з) 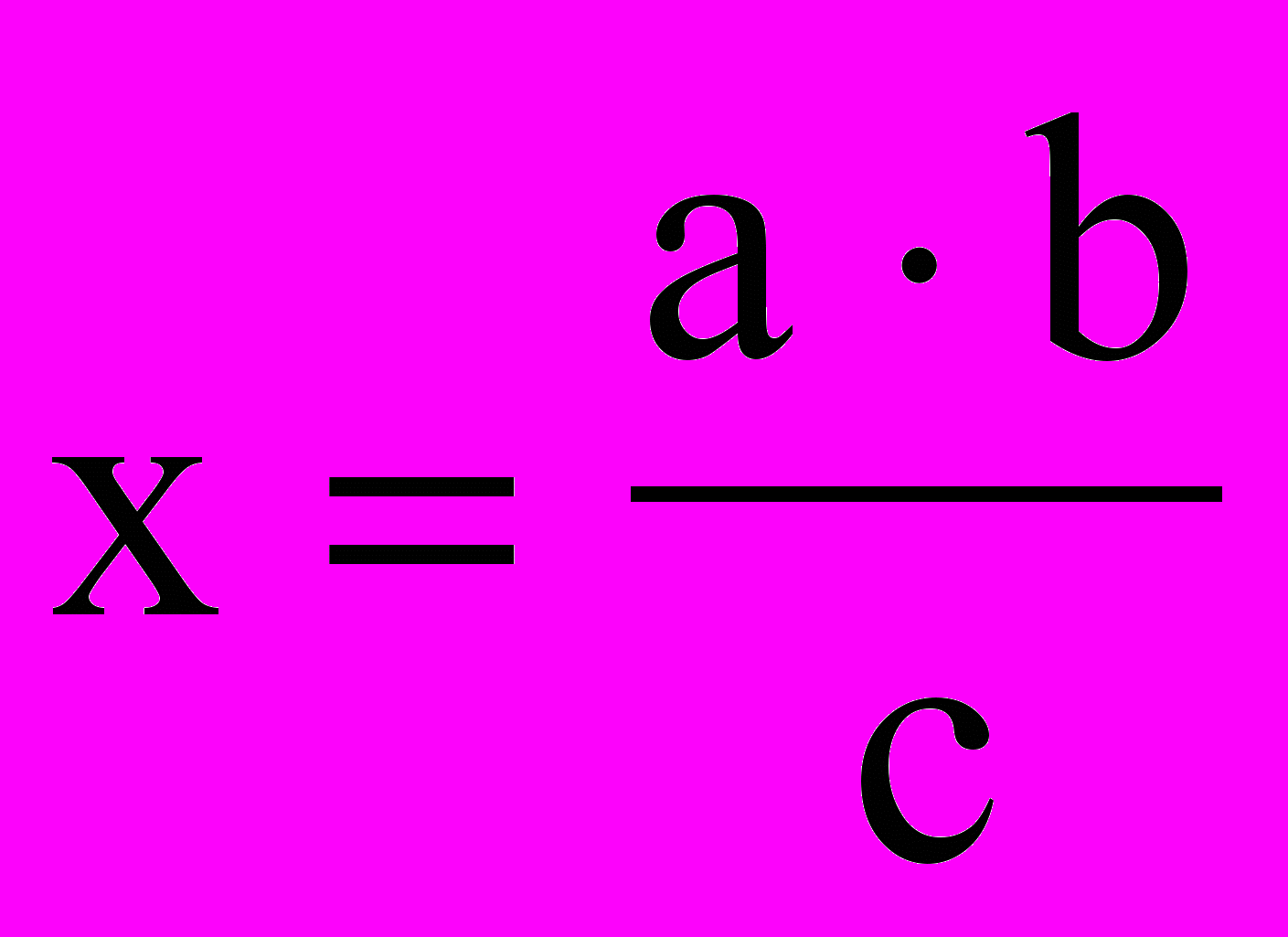
в) х = nа е)
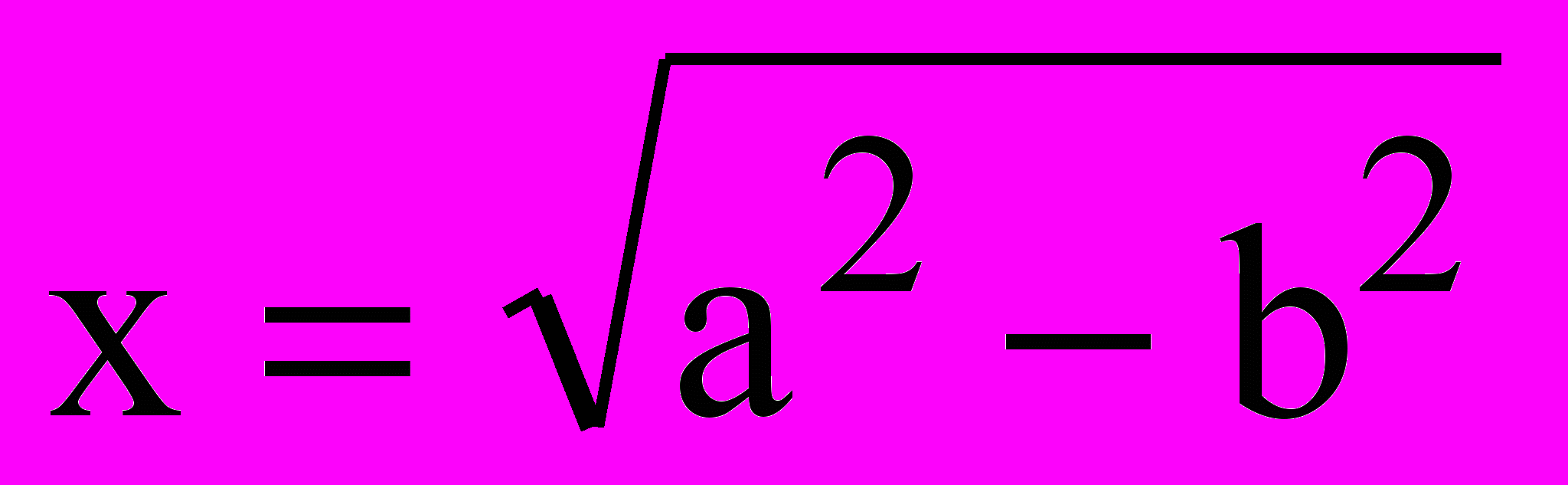 и)
и) 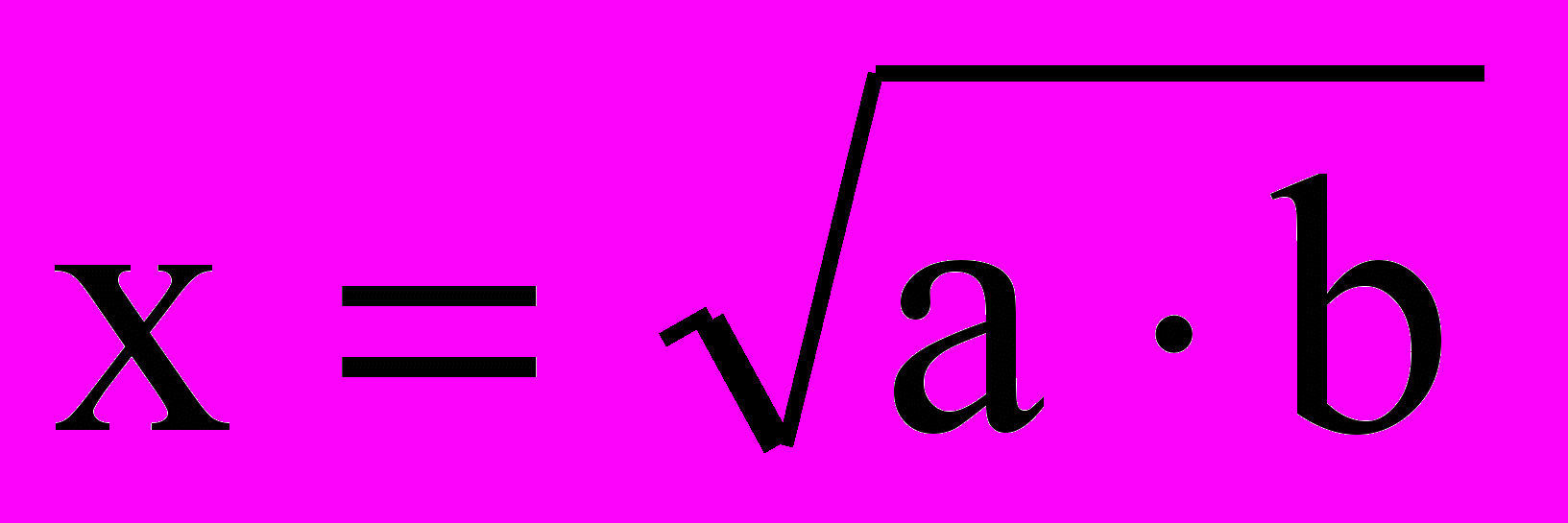
Семинар 1
4.6. “Элементарные задачи на построение фигур” ставит целью рассмотреть затруднения, связанные с подготовкой листа опроса №3.
Литература.
- Б.И. А р г у н о в, М.А. Б а я к. Элементарная геометрия. М.: Просвещение, 1966.
- М.Я. В ы г о т с к и й. Справочник по элементарной математике. М.: Наука, 1971.
- Школьный учебник “Геометрия” (7 кл.).
Приложение 6
Семинар 2
4.7. “Степень точки, относительно окружности”.
- Подготовка к семинару:
а) Прочитать п. 2.6 (параграф 2, гл.1), “Лекции по геометрии”. Ч. 1. С.А. Анищенко.
б) Проработайте текст, пользуясь приложением 13 и 14, подготовьте свои вопросы по данной теме, в том числе по задачам: №№ 35-38, стр. 39.
- Примерные вопросы на семинар:
- Ч
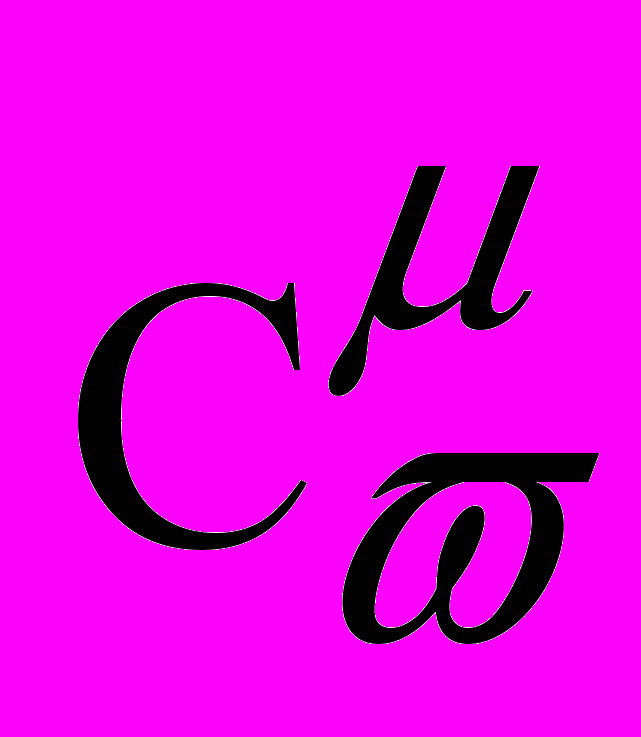
то такое степень точки относительно окружности?
- Как читать запись?
- Как можно вычислить значение?
- Какие значения может принимать?
- Что такое радикальная ось двух окружностей?
- Что называют радикальным центром окружности?
- Как построить радикальную ось двух окружностей?
- Какая теорема является основой построения радикальной оси?
- Какова структурно-логическая схема доказательства теоремы с радикальной оси?
- Как построить радикальный центр трех окружностей?
- Что значит: “окружность ортогонально пересекает две данные окружности”?
- Какие задачи можно решать с использованием понятия “Степень точки относительности окружности”?
- Составьте структурно-логическую схему по теме: “Степень точки относительно окружности”.
“ранее известное”

“новое”


“возможное использование”, в т.ч. в задачах.
Приложение 7
Контрольная работа № 1
