Методические разработки по теме, модулю, разделу преподаваемого предмета». Тема: «Квадратные уравнения в курсе алгебры 8 класса»

Вид материала

Методические разработки

Содержание К уроку по теме «Теорема Виета». Изучение нового материала. Закрепление нового материала. Подведение итогов. Оформление доски Ответы к заданиям урока

Подобный материал:

• Методические разработки по теме, модулю, разделу преподаваемого предмета Тема работы, 300.23kb.
• Задачи данного элективного курса заключаются в следующем: предоставить возможность, 63.74kb.
• А Квадратные уравнения в Древнем Вавилоне, 58.12kb.
• Методика изучения уравнений в курсе алгебры 7-9 классов Примерное содержание, 12.53kb.
• Урок по алгебре в 8-м классе по теме: «Определение квадратного уравнения. Неполные, 70.52kb.
• Урок-лекция по теме «Определение квадратного уравнения. Неполные квадратные уравнения.», 43.99kb.
• Урок №1 Тема : Определение квадратного уравнения. Неполные квадратные уравнения, 419.31kb.
• Решение задач повышенной сложности по теме: «Уравнения и системы уравнений», 141.17kb.
• Конспект урока в 8 классе по теме: «Квадратные уравнения.», 21.81kb.
• Тема 2: Квадратные уравнения, 34.25kb.

К уроку по теме «Теорема Виета».

Актуализация знаний. (на парту)

Задание 1. Разгадать кроссворд.

1
					2
									3
						4
									5
							6
							7

1.Название числа в произведении числа и одной или нескольких переменных.

1. Равенство, содержащее переменную.
   
2. Всякое значение переменной, при которой уравнение обращается в верное равенство.
   
3. Выражение х² – 4ас, для квадратного уравнения.
   
4. Квадратное уравнение, где один из коэффициентов b или с равен 0 .
   
5. Один из способов задания функции.
   
6. Словосочетание в алгебре «Математическая …».
   

Задача – шарада.

Выполните задание и узнайте второе слово темы, вписывая буквы, соответствующие ответу в предложенную таблицу:

№ задания	1	2	3	4	5
Буква

1. Чему равен дискриминант квадратного уравнения х²+ 5х + 6=0
   
2. Сколько корней имеет уравнение х² + 5х + 6 = 0
   
3. Найдите сумму корней уравнения х² + 5х + 6 = 0
   
4. Найдите произведение корней уравнения х² + 5х + 6 = 0
   
5. Один из корней уравнения х² + 5х + с=0 равен 2. Найдите значение с.
   

Ответы:

Т	Е	А	В	И
6	- 5	- 14	1	2

Изучение нового материала.

Задание 2.

1) решите уравнение 1 вариант: х²–х–6 = 0; 2 вариант: х²–8х–20=0. Найдите сумму корней и их произведение. Результаты запишите в таблицу:

	a	b	c	X1	X2	X1+X2	X1 X2
1 вариант
2 вариант

Найдите закономерность и сделайте вывод.

Задание 3.

2) Решите уравнения ( по вариантам) 2х² – 9х+10=0; 5х²+12х+7=0

Найдите сумму корней и их произведение. Результаты запишите в таблицу:

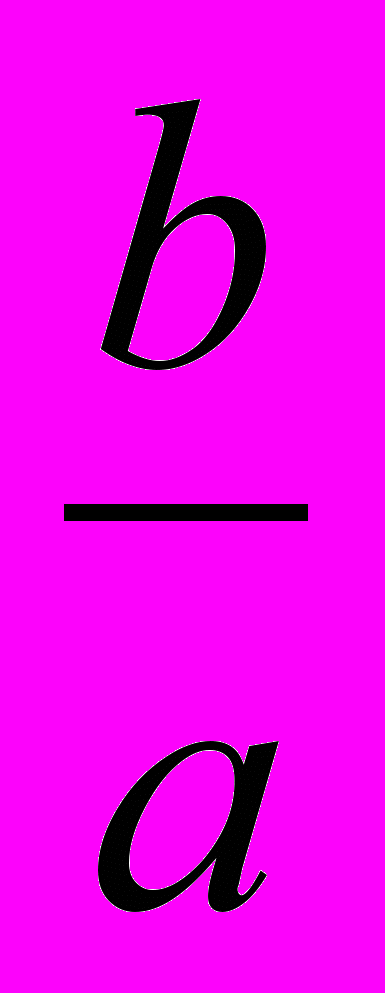
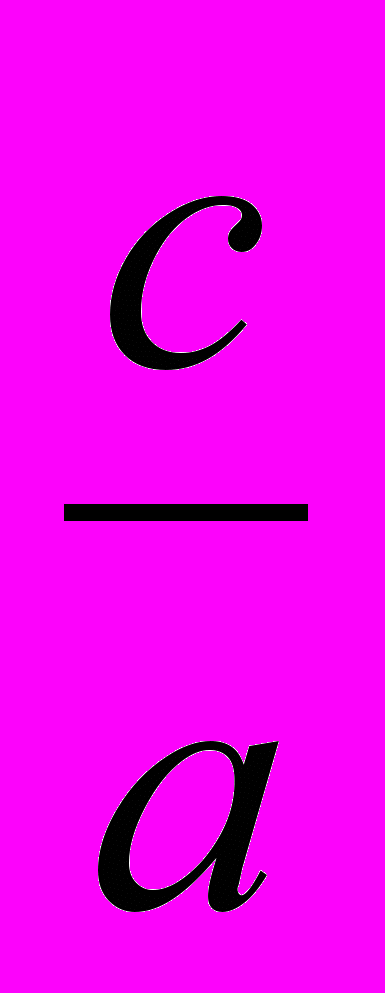
	а	b	c	X1	X2		X1+X2		X1. X2
1 вариант
2 вариант

Найдите закономерность и сделайте вывод.

Задание 4. Работая в парах

1.Сформулируйте теорему.

1. Составьте план доказательства.
   

3. Попытайтесь доказать теорему.


Выбираем «Лучшего теоретика» На доске таблица:

Вывод по таблице 1	Вывод по таблице 2	Формулировка теоремы Виета (письменно)	План доказательства теоремы.	Доказательство теоремы
1. 2. 3.	1. 2. 3.	1. 2. 3.	1. 2. 3.	1. 2. 3.

Ученики, первые справившиеся с заданиями, подходят к учителю, а тот проверяет правильность выполнения и заносит их фамилии в таблицу. Затем дети озвучивают свои записи, остальные – слушают и обсуждают.


Фронтально. Для чего нам может пригодиться данная теорема?

1. Для проверки корней кв. уравнений:
   
2. Для нахождения корней кв. уравнения (без вычисления D;
   
3. Для составления уравнения по заданным корням;
   
4. Для решения уравнений с параметрами;
   
5. Для разложения на множители кв. трехчлена и сокращения дробей (заготовки ответов учитель крепит на доску)
   

Закрепление нового материала.

№ 960; 965; 968; 970 все под (а, б) Выберите и решите самостоятельно те задачи, которые вам понятны.

Сдают тетради. По результатам самостоятельной работы и выполнения домашнего задания выбирают «лучшего практика», поэтому учащиеся еще могут себя проявить.


Подведение итогов.

Рассмотрение задач на применение теоремы Виета мы продолжим на следующем уроке


Домашнее задание.

№964; 967 – уровень А.

№ 971, 972 – уровень В и С.


Оформление доски:

№ Дом. Задание:

Таблица 1 Таблица 2

Теорема Формули-ровка: План доказа-тельства:

Виета Доказа-тельство теоремы:

Т 1 Т 2 Ф П Д

Магнит-ная доска:

Ответы к заданиям урока:

1) Кроссворд

1к

о

э

ф

ф

и

ц

и

е

н

т

2у

р

а

в

н

е

н

и

е

3к

о

р

е

н

ь

4д

и

с

к

р

и

м

и

н

а

н

т

5н

е

п

о

л

н

о

е

6ф

о

р

м

у

л

а

7з

а

д

а

ч

а

1.Название числа в произведении числа и одной или нескольких переменных.

2. Равенство, содержащее переменную.
   
3. Всякое значение переменной, при которой уравнение обращается в верное равенство.
   
4. Выражение х² – 4ас, для квадратного уравнения.
   
5. Квадратное уравнение, где один из коэффициентов b или с равен 0 .
   
6. Один из способов задания функции.
   
7. Словосочетание в алгебре «Математическая …».
   

2) Задача – шарада.

1. Чему равен дискриминант квадратного уравнения х²+ 5х + 6=0 (1)
   
2. Сколько корней имеет уравнение х² + 5х + 6 = 0 (2)
   
3. Найдите сумму корней уравнения х² + 5х + 6 = 0 ( - 5)
   
4. Найдите произведение корней уравнения х² + 5х + 6 = 0 (6)
   
5. Один из корней уравнения х² + 5х + с=0 равен 2. Найдите значение с. (-14)
   

Ответы:

Т	Е	А	В	И
6	- 5	- 14	1	2