Урок №1 Тема : Определение квадратного уравнения. Неполные квадратные уравнения и их решения
| Вид материала | Урок |
- Урок-лекция по теме «Определение квадратного уравнения. Неполные квадратные уравнения.», 43.99kb.
- Урок по алгебре в 8-м классе по теме: «Определение квадратного уравнения. Неполные, 70.52kb.
- А Квадратные уравнения в Древнем Вавилоне, 58.12kb.
- Методические разработки по теме, модулю, разделу преподаваемого предмета». Тема: «Квадратные, 420.13kb.
- Задачи данного элективного курса заключаются в следующем: предоставить возможность, 63.74kb.
- Тема урока: «Дробные рациональные уравнения», 93.81kb.
- Вопросы к экзамену по учебной дисциплине «Дифференциальные уравнения», 32.43kb.
- Тема: Уравнение с двумя переменными. Цели урока, 251.03kb.
- Синявская средняя общеобразовательная школа, 63.47kb.
- Урок в 8 классе ( русский язык и математика) Тема: «Вместе будем обобщать», 71.21kb.
УРОК №1
Тема: Определение квадратного уравнения. Неполные квадратные уравнения и их решения.
Цель:
- Ввести понятия квадратного уравнения, неполного квадратного уравнения. Сформировать умения различать квадратные уравнения, определять коэффициенты квадратного уравнения и по ним определять вид квадратного уравнения. Сформировать умения и навыки решения неполных квадратных уравнений.
- Развивать логическое мышление.
- Воспитывать трудолюбие, развивать самостоятельность.
Тип урока: овладение новыми знаниями и умениями
Оборудование: компьютер, проектор.
Ход урока
- Постановка целей и задач урока.
Учащиеся ставят свои цели и задачи урока и сопоставляют их с целями и задачами, которые ставит на урок учитель.
- Актуализация опорных знаний.
Выполнение устных упражнений.
- Представить в виде многочлена выражения:
(х-2)(2+х); (х-3)2; (у3-у).у; (у-1)(у+2),
- Равносильны ли уравнения:
3х-2=х+3 и 2х-5=0
5х-1=3х-х2 и х2+2х-1=0
0,5х-3=0 и х-6=0
5х2-10х+25=0 и х2-2х+5=0?
Ответы обосновать.
- Решить уравнения:
У-7=0
Х+0,5=0
8х=0
2х-6=0
Х(х+3)=0
Х2-4=0
2х2+8=0
Х2-3=0
III. Объяснение нового материала.
Объяснение нового материала происходит под презентацию.


- Закрепление материала.
Устные упражнения.
- Работа по карточкам.
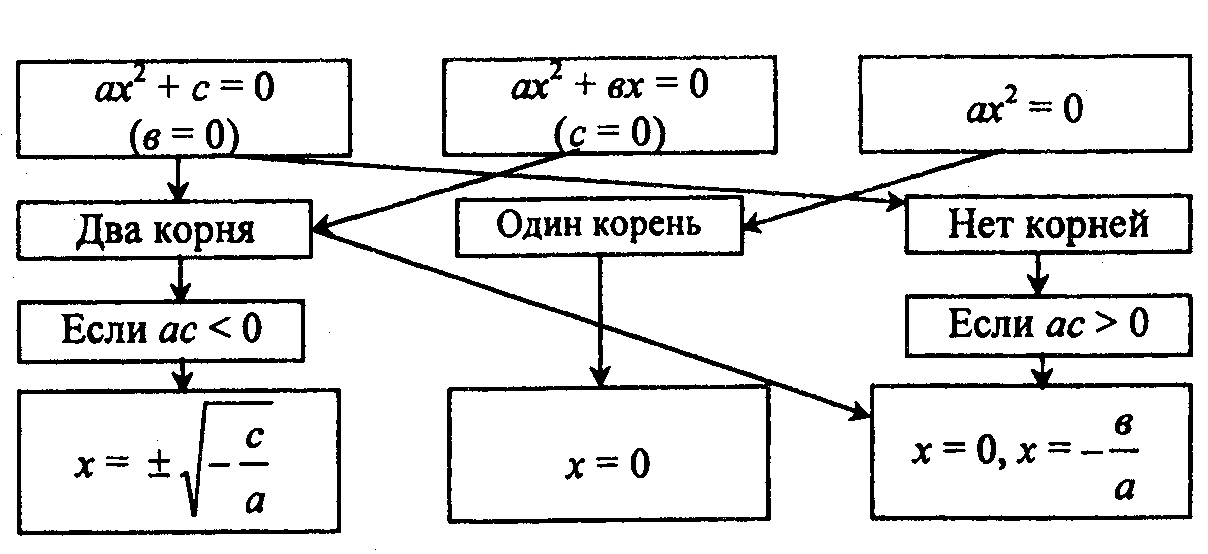
Покажите с помощью стрелок связь между коэффициентами неполного квадратного уравнения.
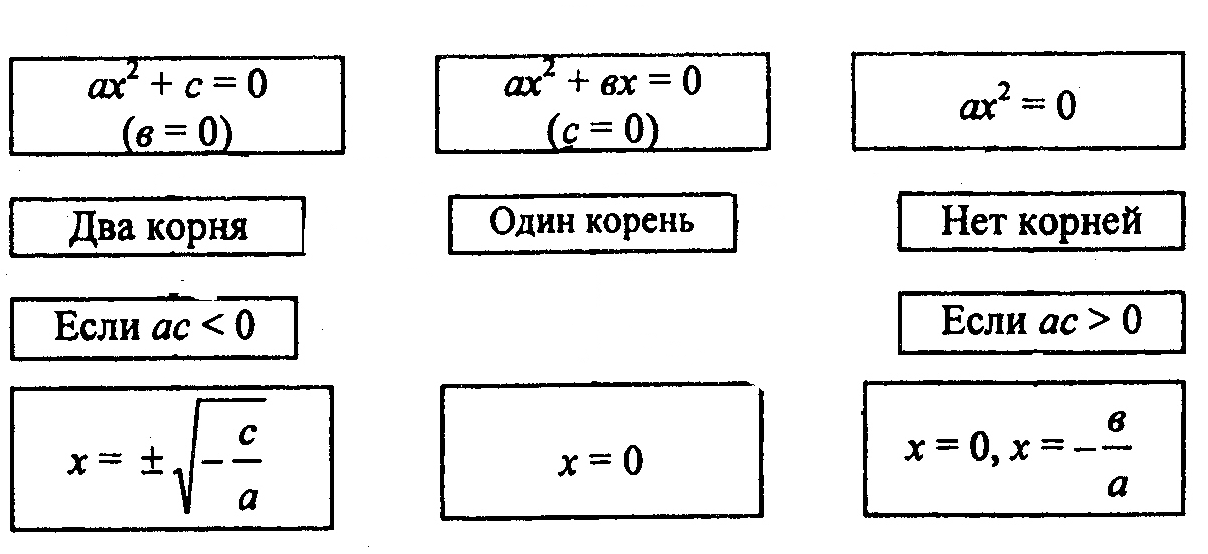
Ответы учащиеся проверяют с помощью взаимопроверки.
- Работа с учебником: №861, 862, 863, 866.
Письменное решение уравнений.
- Работа с учебником.
№ 870, 871, 872Ю 874, 875, 878 – коллективное решение
- Итоги урока.
Выполнение теста.
Учащиеся могут выполнять тест по карточкам, с экрана проектора или с помощью компьютерной программы.
Какое из данных уравнение является квадратным?
- А) 3х2-5х=х-3;
Б) 7x+11=0;
В) x(x-l)=x2-2x;
Г)(х-7):х=0.
- А) 3x=2;
Б) 7x2=9x+12;
В) x(x+3)=x2-2x;
Г) (х+1):х=0.
- А)2х+1=0;
Б)х(х+3)=х2-9х;
В) 5xz+3x=x+7;
Г)(х+4):х=0
4. А)4x2-9x+3=0;
Б) 7x+14=0;
В)х(х+3)=х2-7х+5;
Г)(х-2):х=5.
Выпишите коэффициента а,b, c из квадратного уравнения:
1.x2+2x+7=0.
А) 1, 2, 7.
Б)1,-2,7.
В)1, 2, -7.
Г)-1, 2, 7.
2.3x2-5x-2=0.
А) -3, -5, -2.
Б)3, -5, 2.
В)3, 5, -2.
Г)3, -5, -2.
3.x2-7x+8=0.
А)1, 7, 8.
Б)-1, 7, -8.
В)1, -7, 8.
Г)1, 7, -8.
4.5x2-8x+4=0.
А)5, -9, -4.
Б)5, -9, 4.
В)5, 9, 4.
Г)-5, -9, -4.
5.x2-81=0
А) 1, 0, -81.
Б)0, -81.
В)1, -81.
Г)1, -81, 0
6.4х2-х=0
А)4,-1.
Б)4, 0, -1.
В)4, -1, 0.
Г)4, 1.
- Домашнее задание.
- Выучить теоретический материал, параграф 19.
- Письменно №869, 873, 876,879.
- Повторить упражнения на выделение полного квадрата двучлена.
УРОК №2
Тема: Определение квадратного уравнения. Неполные квадратные уравнения
Цели урока:
- Обобщить и систематизировать изученный материал по теме.
- Формировать умения обобщать, сравнивать, делать выводы.
- Развивать логическое мышление.
- Воспитывать трудолюбие, развивать самостоятельность.
Тип урока: повторительно-обобщающий.
Оборудование: проектор, индивидуальные карточки.
Ход урока:
На доске записан девиз урока:
Математику нельзя
изучать, наблюдая,
как это делает сосед!
Нивен А.
I. Постановка цели урока. Проверка домашнего задания.
Учитель обращает внимание учащихся на девиз урока и сообщает тему урока. Затем вместе с классом формулирует задачи, которые предстоит решить на уроке, приводя к мысли, что основное в математике – это самостоятельный труд.
Проверка домашнего задания по цепочке. Учащиеся комментируют решение заданий . осуществляется самопроверка.
II. Актуализация опорных знаний и умений.
Устный опрос
- Какие уравнения называются квадратными?
- Приведите примеры приведённого квадратного уравнения?
- Как называются числа а, в, с?
- Какие уравнения называются неполными квадратными уравнениями?
- Какие виды неполных квадратных уравнений вы знаете?
- Сколько корней может иметь уравнение каждого вида?
Работа по карточкам в парах
(Двое учащихся работают у доски, а двое – на месте, те, которые решают на месте делают анализ решения товарищей)
Карточка №1
-5у2+8у+8=8у+3
Карточка №2
1-2у+3у2=у2-2у+1
«Проверь себя»
(Остальные учащиеся выполняют в тетрадях, самопроверка с помощью проектора.)
Н
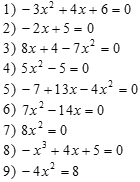 а экране задания:
а экране задания: | Задание №1 Выпишите под какими номерами стоят квадратные уравнения? Задание №2 Дайте характеристику каждого квадратного уравнения. Задание №3 Сколько корней имеет уравнение 4), 6), 7), 9)? | |
III. Работа по группам: (по заданиям с учебника)
| Группа №1 (учащиеся со средним уровнем) № 877(а), 880(б) Группа №2 (учащиеся с достаточным уровнем) №887(а),889(б, г) Группа № 3 (учащиеся с высоким уровнем) № 892(а), 896(б) | |
Представители групп предлагают план решения уравнения и демонстрируют решение на доске.
IV. Самостоятельная работа.
Учащимся предлагается решить уравнения. Ответы уравнений закодированы буквами на экране. В результате успешного выполнения работы в тетрадях у учащихся появляется предложение « Это – успех! »
| О | Э | У | С | Х | Т | П | Е | - | ! |
| 0 | 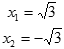 | 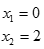 | 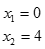 | 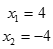 | 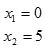 | 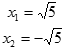 | 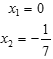 | Корней нет | 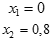 |

V. Решение задач
(тот, кто быстро выполнил самостоятельную работу, получает карточку)
Карточка
| Разность двух чисел равна 2, а половина произведения этих чисел равна их среднему арифметическому. Найдите эти числа. |
VI. Итог урока
VII. Домашнее задание.
Параграф 19, № 879, 881 (средний уровень)
№ 886, 890 (достаточный уровень)
№897, 899 (высокий уровень)
№ 917(а) на повторение всем учащимся
УРОК №3
Тема: Формула корней квадратного уравнения.
Цель урока:
- Ввести понятие дискриминанта и исследовать коэффициенты квадратного трехчлена.
- Развивать познавательную активность учащихся и логическое мышление.
- Последовательно формировать у учащихся умение выдвигать гипотезы, аргументировано доказывать их.
- Воспитывать трудолюбие, развивать самостоятельность.
Тип урока: Овладение новыми знаниями и умениями
Ход урока
- Тема и цель урока. Проверка домашнего задания.
1)Устный опрос.
1. Что такое уравнение?
2. Что значит решить уравнение?
3. Что такое корень уравнения?
4. Какое уравнение называется квадратным?
5. Почему коэффициент а не может равняться нулю?
6. Какие существуют квадратные уравнения?
7. Как получаются неполные квадратные уравнения?
2) ответы на вопросы по решению домашнего задания.
II. Мотивация учебной деятельности.
Учащимся предлагаются несколько уравнений.
2x2+x+3=0 и 2x2-x+3=0
2x2-x-3=0 и 2x2+x-3=0
3x2-6x+3=0 и 3x2+6x+3=0
- Какие из следующих уравнений, на ваш взгляд, имеют корни, а какие – не имеют корней. Можете ли вы ответить на этот вопрос, не решая уравнений?
(ответ детей)
- Как вы думаете, количество корней квадратного уравнения определяется:
- одним коэффициентом;
- двумя коэффициентами;
- тремя коэффициентами;
- некоторым выражением, составленным из коэффициентов?
(дискуссия детей)
III. Объяснение нового материала.
Чтобы правильно ответить на эти вопросы, решим данные уравнения.
Да, вы правы, число корней квадратного уравнения ax2+bx+c=0 зависит от выражения составленного из коэффициентов этого уравнения. Что это за выражение? Как оно влияет на количество корней? Проанализируем формулу корней квадратного уравнения.
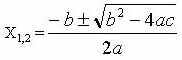
1. Если b2-4ac >0, то квадратное уравнение имеет два различных действительных корня.
2. Если b2-4ac =0, то квадратное уравнение имеет два совпадающих действительных корня.
3. Если b2-4ac <0, то квадратное уравнение не имеет действительных корней.
Ответь на вопросы:
- Влияет ли знак второго коэффициента на количество корней квадратного уравнения?
- Верно ли, что если в квадратном уравнении коэффициенты a и с имеют противоположные знаки, то это уравнение обязательно имеет два различных корня.
- Что вы можете сказать о количестве корней квадратного уравнения, у которого коэффициенты а и с одного знака.
Выполняя задание, вы, конечно, обратили внимание на то, что “различителем” числа корней квадратного уравнения является выражение b2- 4ас.
Ему дано специальное имя – дискриминант (от discriminantis – по латыни “различающий”, “разделяющий”).
Дискриминант обозначается буквой D:
D= b2- 4ас
А в толковом математическом словаре (дети смотрят сами) дискриминант квадратного трёхчлена – величина, определяющая характер его корней.
Ч
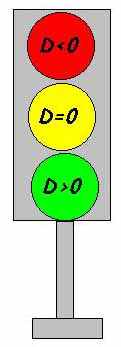 то общего между понятием “светофор” и “дискриминант”?
то общего между понятием “светофор” и “дискриминант”? (Отвечая, дети подходят по очереди к светофору и вставляют карточку на место нужного цвета).
Теперь формулу корней квадратного уравнения можно записать так:
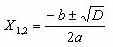
А теперь, ребята, помогите составить ещё один алгоритм решения квадратного уравнения
(Дети сами составляют алгоритм).
АЛГОРИТМ
1. Выделить в квадратном уравнении коэффициенты.
2. Вычислить дискриминант D.
3. Если D<0, то уравнение не имеет действительных корней.
Если D>или=0, то вычислить корни по формуле.
После этого на доску вывешивается таблица с заранее составленным учителем алгоритмом, и дети сверяют собственный вариант с истинным.
IV.Закрепление материала.
Коллективное решение.
На доске показать решение двух уравнений:
1. 2х2-9х+10 = 0
2. 3х2-5х+7 = 0
Дифференцированный подход.
Детям предложить тест.

Для детей, которым трудно дается математика.
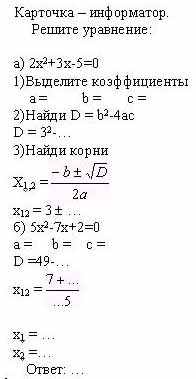
Карточка повышенной сложности
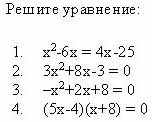
V. Подведение итога урока.
Эстафета «Кто быстрее»
| № | а | b | c | Уравнение |
| 1 | 3 | -1 | 0 | |
| 2 | 1 | 0 | -25 | |
| 3 | 2 | 1 | -3 | |
| 4 | 5 | 0 | 0 | |
| 5 | 1 | -3 | -10 | |
| 6 | 7 | -5 | 6 | |
| 7 | 1 | -4 | 3 | |
| 8 | 9 | -12 | 4 | |
| 9 | -3 | -2 | 5 | |
| 10 | 0 | 3 | 6 | |
Ответы
Уравнения.
- 3х2-х=0
- х2-25=0
- 2х2+х-3=0
- 5х2=0
- х2-3х-10=0
- 7х2-5х+6=0
- х2-4х+3=0
- 9х2-12х+4=0
- -3х2-2х+5=0
- 3х+6=0
VIДомашнее задание:
Параграф 20, № 930, 932, 933
УРОК №4
Тема: Формула корней квадратного уравнения.
Цель урока:
- Отработать умения и навыки решения квадратных уравнений с использованием формул корней.
- Знакомство с новым способом решения квадратных уравнений.
- Развивать логическое мышление.
- Воспитывать трудолюбие, развивать самостоятельность.
Тип урока: закрепление знаний и умений.
Ход урока:
- Постановка целей и задач урока.
- Актуализация опорных знаний.
На доске записаны уравнения:
1)х2 + 2х – 8 = 0;
2) 2х2 + 5х = 0;
3) 3х2 = 0;
4) 2х2 + 3х – 8 = 0;
5) х2 – 5х + 1 = 0;
6) 6х2 + 12 = 0.
Вопросы:
- Какие уравнения записаны на доске?
- Какие уравнения называются квадратными?
- Прочтите полные квадратные уравнения.
- Какие уравнения называются полными?
- Как называются уравнения, у которых первый коэффициент равен 1? Приведите примеры.
- Какое выражение называется дискриминантом?
- Сколько корней может иметь квадратное уравнение? От чего это зависит?
- Как называются уравнения под цифрами 2; 3; 6? Почему?
- Как решаются уравнения под цифрой 2?
- Чему равен х в уравнении под цифрой 3?
- Что можно сказать о решении уравнения под цифрой 6?
- Проверка домашнего задания.
Проверка в парах. Ученики меняются тетрадями и проверяют задания по готовому решению, оформленному на доске одном из учеников.
IV. Математический диктант
(задания для второго варианта даны в скобках).
Двое решают на разворотах доски:
1. Запишите квадратное уравнение, у которого первый коэффициент равен 3 [- 5], второй коэффициент равен - 5 [3], а свободный член равен 2.
2. Запишите неполное квадратное уравнение, у которого первый коэффициент равен 3 [5], второй – 7 [3], и решите его.
3. Найдите дискриминант квадратного уравнения 3x2 – 8x – 3 = 0,
[5y2 – 6y +1 = 0].
4. Сколько корней имеет это уравнение?
5. При каком условии квадратное уравнение не имеет корней? [имеет два одинаковых корня?]
V. Решение квадратных уравнений:
Задание достаточного уровня:
1) х2 + 2х – 80 = 0;
2) 4х2 + 4х + 1 = 0;
3) 3у2 – 3у + 1 = 0.
Задание высокого уровня:
1) 5х2 = 9х + 2;
2) (х + 4 )2 = 3х + 40;
3) (3х – 1)(х + 3) =х(1 + 6х).
На доске одновременно решаются первые три уравнения, затем следующие три. Решения разбираются. Слабые ученики работают по карточкам.
Работа по карточкам.
Дано уравнение 3х2 – 7х + 4 = 0.
- Запиши, чему равны а, в, с.
- Найди, чему равен дискриминант Д.
- Найди по формуле, чему равны х1 и х2.
- Запиши ответ.
Аналогично решаются уравнения:
5у2 – 6у + 1 = 0;
2у2 – 9у + 10 = 0;
у2 – 10у – 24 = 0.
VI. Объяснение нового материала.
Сегодня мы познакомимся еще с одним способом решения квадратных уравнений, который позволит быстро находить корни уравнения.
Назовите коэффициенты в следующих уравнениях и найдите их сумму:
| 1) х2 – 5х + 1 = 0; | 1 – 5 + 1 = - 3; |
| 2) 9х2 – 6х + 10 = 0; | 9 – 6 + 10 = 0; |
| 3) х2 + 2х – 2 = 0; | 1 + 2 – 2 = 0; |
| 4) х2 - 3х – 1 = 0; | 1 – 3 – 1 = - 3. |
У всех этих уравнений сумма коэффициентов различна.
В данных уравнения выпишите решения и найдите, чему равна сумма коэффициентов и свободного члена:
| 1) х2 + х – 2 = 0, | х1 = 1, | х2 = - 2, | 1 + 1 – 2 = 0; |
| 2) х2 + 2х – 3 = 0, | х1 = 1, | х2 = - 3, | 1 + 2 – 3 = 0; |
| 3) х2 – 3х + 2 = 0, | х1 = 1, | х2 = 2, | 1 – 3 + 2 = 0; |
| 4) 5х2 – 8х + 3 = 0, | х1 = 1, | х2 = 3/5, | 5 – 8 + 3 = 0 . |
отыщите закономерность:
- в корнях уравнений;
- в соответствии между корнями и коэффициентами;
- в сумме коэффициентов.
Попытайтесь сформулировать правило нахождения корней.
Если в квадратном уравнении
ах2 + вх + с = 0
если а + в + с =0, то х1 = 1, х2 = с/а;
если а = 1, то х1 = 1, х2 = с.
VII. Решите уравнения:
3х2 – 7х + 4 = 0;
5х2 – 8х + 3 = 0;
3х2 + 11х – 14 = 0.
VIII. Проведение дифференцированной самостоятельной работы на два варианта.
1. 2х2 + х – 3 = 0; 5х2 – 18х + 16 = 0;
[5x2 + x - 6 = 0; x2 – 18x + 80 = 0].
2. 5x2 – 16x + 3 = 0; 36y2 – 12y + 1 = 0;
[x2 – 22x – 23 = 0; 5x2 + 9x + 4 = 0].
3. – x2 = 5x – 14; (2x – 3)2 = 11x – 19;
[6x + 9 = x2; - x(x + 7) = (x – 2)(x + +2)].
IX. Домашнее задание.
Составить и решить три квадратных уравнения, таких, что а + в + с = 0, решить уравнение (х + 1)2 = (2х – 1)2.
X. Подведение итогов урока.
1.Сегодня на уроке мы решали квадратные уравнения по формулам. Ответьте на вопросы: сколько решений имеет уравнение в зависимости от знака дискриминанта? Какое новое правило решения квадратных уравнений мы вывели на уроке?
2.Выполнение компьютерного теста.
Найти дискриминант уравнения
1.2у2+3у+1=0. 2.2у2+5у+2=0.
А) 11; Б) 17; А) 41; Б) 9;
В)-5; Г)1. В)-11; Г) 21.
3.х2-6х+5=0. 4.х2-7х+12=0.
А) 16; Б) -56; А) -1; Б) -97;
В)-16; Г)56. В)1; Г) 97.
Сколько корней имеет уравнение?
1.х2-9х+14=0? 2. х2-8х+15=0?
А) два; Б) один; А) два; Б) один;
В)не имеет корней; В)не имеет корней;
Г)множество. Г) множество
3.2х2+х+2=0? 4. Зх2+х+4=0?
А) два; Б) один; А) два; Б) один;
В) не имеет корней; В) не имеет корней;
Г) множество. Г) множество.
УРОК №5
