Урок №1 Тема : Определение квадратного уравнения. Неполные квадратные уравнения и их решения
| Вид материала | Урок |
- Урок-лекция по теме «Определение квадратного уравнения. Неполные квадратные уравнения.», 43.99kb.
- Урок по алгебре в 8-м классе по теме: «Определение квадратного уравнения. Неполные, 70.52kb.
- А Квадратные уравнения в Древнем Вавилоне, 58.12kb.
- Методические разработки по теме, модулю, разделу преподаваемого предмета». Тема: «Квадратные, 420.13kb.
- Задачи данного элективного курса заключаются в следующем: предоставить возможность, 63.74kb.
- Тема урока: «Дробные рациональные уравнения», 93.81kb.
- Вопросы к экзамену по учебной дисциплине «Дифференциальные уравнения», 32.43kb.
- Тема: Уравнение с двумя переменными. Цели урока, 251.03kb.
- Синявская средняя общеобразовательная школа, 63.47kb.
- Урок в 8 классе ( русский язык и математика) Тема: «Вместе будем обобщать», 71.21kb.
Тема и цель урока.
Здравствуйте, ребята. Нам предстоит поработать над очень важной темой: “Решение квадратных уравнений”. Вы уже достаточно знаете и умеете по этой теме, поэтому наша с вами задача: обобщить и сложить в систему все те знания и умения, которыми вы владеете.
Чтобы у нас царила атмосфера доброжелательности, предлагаю начать урок с таких слов:
В класс вошел – не хмурь лица,
Будь разумным до конца.
Ты не зритель и не гость –
Ты программы нашей гвоздь.
Не ломайся, не смущайся,
Всем законам подчиняйся.
А законы у нас сегодня будут такие: каждый из вас имеет возможность получить оценку за урок по результатам работы на различных его этапах. Для этого у вас на партах лежат карты результативности, в которые вы будете фиксировать свои успех в баллах. И еще один не обсуждаемый закон: для ответа на поставленный вопрос вы поднимаете руку и ни в коем случае не перебиваете друг друга. Желаю всем удачи.
Карта результативности.
Приступим к работе. Для того чтобы включиться в работу и сконцентрироваться предлагаю вам небольшую устную разминку. Но вопросы будут не только по теме урока, проверяем ваше внимание, и умение переключаться. За каждый правильный ответ в колонку “Разминка” вы по моему указанию ставите 1 балл.
Вопросы теоретической разминки:
Попрошу открыть тетради, записать число и тему сегодняшнего урока.
“Решение квадратных уравнений”.
Уравнения с давних времен волновали умы человечества. По этому поводу у английского поэта средних веков Чосера есть прекрасные строки, предлагаю сделать их эпиграфом нашего урока:
Посредством уравнений, теорем
Я уйму всяких разрешил проблем.
Квадратные уравнения тоже не исключение. Они очень важны и для математики, и для других наук. На ближайших уроках математики вам предстоит решать текстовые задачи и вот тут-то необходимо уметь быстро и умело справляться с решением квадратных уравнений.
Раз уж мы говорим об уравнениях, давайте вспомним – что это такое?
- Равенство, содержащее неизвестное.
Является ли уравнением выражение (х + 1)(х – 4) = 0?
Да
Запишите его в тетрадях. Каким наиболее рациональным способом мы можем его решить?
Приравнивая каждый множитель к нулю. Произведение равно нулю, когда один из множителей равен нулю, а другой при этом имеет смысл.
Хорошо.
Решите, пожалуйста, это уравнение.
- х = -1 и х = 4.
А можно ли его решить другим способом?
Да, его можно привести к квадратному.
Напомните, какие уравнения называются квадратными?
Уравнения вида ах2 + вх + с = 0.
Приведите наше уравнение к такому виду.
х2 – 3х – 4 = 0
Назовите его коэффициенты. А что еще вы можете сказать об этом уравнении?
- Оно полное и приведенное.
А какие еще виды квадратных уравнений вам известны?
Отвечают
Хорошо.
Теперь давайте проверим, насколько хорошо вы умеете определять виды квадратных уравнений. Вашему вниманию предлагается тест, в котором записаны, пять уравнений. Напротив каждой колонки вы ставите плюс, если оно принадлежит к данному виду.
Тест “Виды квадратных уравнений”
Ребята выполняют работу, а затем меняются листочками и по ключу проверяют ответы, оценивая работу товарища. Результат записывается в колонку “Оценочный балл”, а затем в “Карту результативности”( максимально 5 баллов).
Ключ к тесту:
М
Карточка:
Выбери из представленных в задании уравнений те, которые являются квадратными:
олодцы. С видами квадратных уравнений мы разобрались. Кстати, а вы знаете, когда появились первые квадратные уравнения?
Очень давно. Их решали в Вавилоне около 2000 лет до нашей эры, а Европа три года назад отпраздновала 800летие квадратных уравнений, потому что именно в 1202 году итальянский ученый Леонард Фибоначчи изложил формулы квадратного уравнения. И лишь в 17 веке, благодаря Ньютону, Декарту и другим ученым эти формулы приняли современный вид.
А с каким еще понятием мы постоянно сталкиваемся при решении квадратных уравнений?
С дискриминантом
А вот понятие Д придумал английский ученый Сильвестр, он называл себя даже “математическим Адамом” за множество придуманных терминов. А зачем он нам нужен?
Он определяет число корней квадратного уравнения.
И как количество корней зависит от Д?
Дети перечисляют случаи.
Итак, давайте еще раз проговорим алгоритм решения полного квадратного уравнения.
Проговаривают.
Ну что ж, приступим к практической части нашего урока.
Чтобы решить уравнение,
Корни его отыскать.
Нужно немного терпения,
Ручку, перо и тетрадь.
Перед вами список различных уравнений. Посмотрите внимательно на уравнения 1-3 и скажите: являются ли эти уравнения квадратными?
Да. Потому что наивысшая степень 2.
А что нас смущает во внешнем виде этих уравнений?
Они записаны не в стандартном виде.
Итак, преобразуйте данные уравнения к стандартному виду (3 балла).
А каким методом решаются следующие два уравнения?
Метод введения новой переменной.
Вспомним, как решаются такие уравнения, поработаем вместе у доски.
Хорошо. Вместе мы поработали. Теперь посмотрим, как вы умеете работать самостоятельно. Вам предлагается трехуровневая работа. Если вы еще не уверены в своих силах и желаете закрепить решение уравнение, то выбираете уровень А(6 балла) .Если считаете, что материал усвоен хорошо – В (9 баллов). Ну, а если желаете испробовать свои силы на более сложных заданиях – уровень С (12 баллов)для вас. В процессе решения я проверяю ваши работы и проставляю заработанные баллы.
Вариант 1.
Уровень А
№1. Для каждого уравнения вида ax2 + bx + c = 0 укажите значения a, b, c.
а) 3х2 + 6х – 6 = 0, б) х2 - 4х + 4 = 0
№2. Продолжите вычисление дискриминанта D квадратного уравнения ax2 + bx + c = 0 по формуле D = b2 - 4ac.
5х2 - 7х + 2 = 0, D = b2 - 4ac = (-7)2 – 4· 5 · 2 = …;
№3. Закончите решение уравнения 3х2 - 5х – 2 = 0.
D = b2 - 4ac = (-5)2- 4· 3·(-2) = 49; х1 = … х2=…
Уровень В Решите уравнение: а) 6х2 – 4х + 32 = 0; б) х2 + 5х - 6 = 0.
Уровень С
Решите уравнение: а) -5х2 – 4х + 28 = 0; б) 2х2–8х–2=0. x1=2+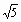
, x2=2–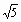
Доп. задание. При каком значении а уравнение х2 - 2ах + 3 = 0 имеет один корень?
Вариант 2.
Уровень А
№1. Для каждого уравнения вида ax2 + bx + c = 0 укажите значения a, b, c.
а) 4х2 - 8х + 6 = 0, б) х2 + 2х - 4 = 0
№2. Продолжите вычисление дискриминанта D квадратного уравнения ax2 + bx + c = 0 по формуле D = b2 - 4ac.
5х2 + 8х - 4 = 0, D = b2 - 4ac = 82 – 4· 5 · (- 4) = …;
№3. Закончите решение уравнения х2 - 6х + 5 = 0.
D = b2 - 4ac = (-6 )2 - 4· 1·5 = 16; х1 = … х2=…
Уровень В Решите уравнение: а) 3х2 – 2х + 16 = 0; б) 3х2 - 5х + 2 = 0.
Уровень С
Решите уравнение: а) 5х2 + 4х - 28 = 0; б) х2 – 6х + 7 = 0; x1=3+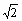
, x2=3–.
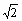Доп.задание. При каком значении а уравнение х2 + 3ах + а = 0 имеет один корень.
IV. Подведение итогов.
Итак, мы проделали большую работу. Повторили всю теорию, касающуюся полных квадратных уравнений. Прорешали различные их виды как вместе, так и вы сами. Вы старательно зарабатывали баллы, настало время подвести итог.
Подсчитайте сумму баллов заработанных в течение урока.
Критерии оценивания:
25 – 30 баллов – “12”.
19 – 24 баллов – “9”.
10 -18 баллов – “6”.
Выставляются оценки.
Да, кстати, у меня для вас есть еще один сюрприз, который я спрятала в классе. Для того, чтобы узнать, где он находится надо решить следующее задание:
В уравнении х2 – рх + 3 = 0 один из корней равен 9. Если вы найдете число р, то узнаете номер парты, а второй корень укажет ряд, на котором находится парта с сюрпризом.
Сюрпризом будет конвертик со следующей надписью:
Франсуа Виет
Жизнь Виета представляет для нас интерес во многих отношениях.
XV век в Западной Европе был веком ожесточенных религиозных волнений, и к началу XVI целый ряд стран отпал от католической церкви.
Всесильная католическая церковь преследовала и убивала всякую мысль, в которой усматривала отклонение от своих учений. Церковный суд – инквизиция – всех попавшихся под подозрение карал вплоть до сожжения на костре, а имущество казненных отбирал в пользу церкви. Не один ученый погиб в руках инквизиции. В их числе были и математики.
Испанский математик Вальмес в 1486 году как-то в семейном кругу обмолвился о том, что нашел формулу для решения уравнения четвертой степени. В числе гостей оказался влиятельный инквизитор. Услышав слова Вальмеса, он заявил, что волей Божьей решать эти уравнения человеку не дано, а найти формулу можно было только с помощью дьявола.
В ту же ночь Вальмес был брошен в тюрьму, а через три недели сожжен на костре за связь с дьяволом. Лишь через 100 лет решение этих уравнений было найдено вторично.
Мэтр Виет также был на волосок от костра.
В ту пору наиболее могущественное государство в Европе, Испания вела победоносную войну с Францией.
Однажды французам удалось перехватить приказы испанского правительства командованию своих войск, написанные очень сложным шифром (тайнописью). Виет с помощью математики сумел найти ключ к этому шифру. С этих пор французы, зная планы испанцев, с успехом предупреждали их наступления.
Инквизиция обвинила Виета в том, что он прибегнул к помощи дьявола, и приговорила к сожжению на костре. Но так как французы благодаря Виету в дальнейшем побеждали, он не был выдан инквизиции.
В родном городке Виет был лучшим адвокатом, а позднее стал королевским советником. Но главным делом его жизни была математика. Биографы Виета пишут, что он мог несколько ночей подряд не спать, решая очередную математическую задачу.
УРОК №8
Тема: Контрольная работа по теме «Квадратные уравнения. Формула корней квадратного уравнения. Теорема Виета.»
Цель:
Тип урока: Урок контроля знаний и умений.
Ход урока.
Вариант №1
1 ЧАСТЬ.
А) 11 Б)17 В)-5 Г)1
2) Решите уравнение: х2+5х=0
А)0;5 Б)-5;0 В)-5 Г)5
3)Выпиши коэффициенты квадратного уравнения: 5х2-9х+4=0
А) 5,-9,-4 Б)5,9,4. В)5,-9,4 Г)-5, -9, -4
4) реши уравнение х2-6х+8=0
А)2,4 Б)решение нет В)-4;-2 Г)другой ответ
5)Не решая уравнения найдите сумму и произведение корней уравнения х2+5х-24=0
А) 5;24 Б) 5;-24 В)-5;-24 Г)-5;24
6)реши уравнение (у-6)(у+8)=-48
А) 2;0 Б)-2 В)0 Г) решений нет
1)х4-5х2-36=0
2)при каком значении k уравнение имеет только один корень : 2х2+4х+ k=0
3 ЧАСТЬ
1)(х2-2)2+3(х2-2)+2=0
2) (2х-1)(2х+1)-(х-3)(х+1)=18
Вариант №2
1)Вычислите дискриминант уравнения: 2х2+5х+2=0
А)41 Б)9 В)-11 Г)21
2) Решите уравнение: х2+3х=0
А)0;3 Б)-3;0 В)-3 Г)3
3)Выпиши коэффициенты квадратного уравнения: 3х2-5х-2=0
А) -3,-5,-2 Б)3,5,-2. В)3,-5,2 Г)3,-5,-2
4) реши уравнение х2-4х+6=0
А)-3,-2 Б)-1,6 В)2,3 Г)другой ответ
5)Не решая уравнения найдите сумму и произведение корней уравнения х2+5х-14=0
А) 5;-14 Б) 5;14 В)-5;-14 Г)-5;14
6)реши уравнение (у+5)(у-9)=-45
А) 4;0 Б)4 В)0 Г) решений нет
1)х4-6х2+8=0
2)при каком значении k уравнение имеет только один корень : 2х2 -6х+ k=0
3 ЧАСТЬ
1)(х2+3)2-7(х2+3)+12=0
2) (3х-1)(3х+1)-(х+2)(х-1)=8
Решение задание, которые вызвали трудности при решении.
Повторить : определение многочлена, разложение многочленов на множитель, основные свойства дробей, сокращение дробей.
Автор: Любимченко О.В., вчитель математики, Торезька гімназія суспільно-гуманітарного профілю Донецької області
- Мотивация учебной деятельности.
Здравствуйте, ребята. Нам предстоит поработать над очень важной темой: “Решение квадратных уравнений”. Вы уже достаточно знаете и умеете по этой теме, поэтому наша с вами задача: обобщить и сложить в систему все те знания и умения, которыми вы владеете.
Чтобы у нас царила атмосфера доброжелательности, предлагаю начать урок с таких слов:
В класс вошел – не хмурь лица,
Будь разумным до конца.
Ты не зритель и не гость –
Ты программы нашей гвоздь.
Не ломайся, не смущайся,
Всем законам подчиняйся.
А законы у нас сегодня будут такие: каждый из вас имеет возможность получить оценку за урок по результатам работы на различных его этапах. Для этого у вас на партах лежат карты результативности, в которые вы будете фиксировать свои успех в баллах. И еще один не обсуждаемый закон: для ответа на поставленный вопрос вы поднимаете руку и ни в коем случае не перебиваете друг друга. Желаю всем удачи.
Карта результативности.
| Ф.И. | Разминка | Тест | Вопросы теории | Решение уравнений | Сам. работа | ИТОГО |
| Количество баллов | | | | | | |
- Выполнение работы
Приступим к работе. Для того чтобы включиться в работу и сконцентрироваться предлагаю вам небольшую устную разминку. Но вопросы будут не только по теме урока, проверяем ваше внимание, и умение переключаться. За каждый правильный ответ в колонку “Разминка” вы по моему указанию ставите 1 балл.
Вопросы теоретической разминки:
- Какое название имеет уравнение второй степени?
- Сформулируйте определение квадратного уравнения.
- Объясните, в чем заключается смысл ограничения в определении квадратного уравнения (а
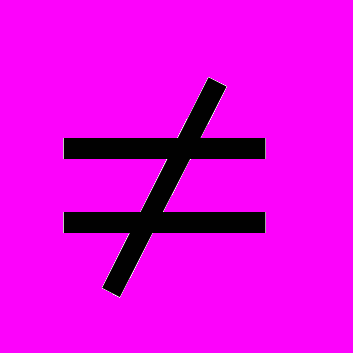0).
- Перечислите виды квадратных уравнений.
- Что значит решить уравнение?
- Приведите примеры квадратных уравнений различных видов.
- От чего зависит количество корней квадратного уравнения?
- Сколько корней имеет квадратное уравнение, если D больше 0?
- Сколько корней имеет квадратное уравнение, если дискриминант меньше 0
- Какое квадратное уравнение называется приведенным? Приведите пример.
- Есть у любого слова, у растения и может быть у уравнения?
Попрошу открыть тетради, записать число и тему сегодняшнего урока.
“Решение квадратных уравнений”.
Уравнения с давних времен волновали умы человечества. По этому поводу у английского поэта средних веков Чосера есть прекрасные строки, предлагаю сделать их эпиграфом нашего урока:
Посредством уравнений, теорем
Я уйму всяких разрешил проблем.
Квадратные уравнения тоже не исключение. Они очень важны и для математики, и для других наук. На ближайших уроках математики вам предстоит решать текстовые задачи и вот тут-то необходимо уметь быстро и умело справляться с решением квадратных уравнений.
Раз уж мы говорим об уравнениях, давайте вспомним – что это такое?
- Равенство, содержащее неизвестное.
Является ли уравнением выражение (х + 1)(х – 4) = 0?
Да
Запишите его в тетрадях. Каким наиболее рациональным способом мы можем его решить?
Приравнивая каждый множитель к нулю. Произведение равно нулю, когда один из множителей равен нулю, а другой при этом имеет смысл.
Хорошо.
Решите, пожалуйста, это уравнение.
- х = -1 и х = 4.
А можно ли его решить другим способом?
Да, его можно привести к квадратному.
Напомните, какие уравнения называются квадратными?
Уравнения вида ах2 + вх + с = 0.
Приведите наше уравнение к такому виду.
х2 – 3х – 4 = 0
Назовите его коэффициенты. А что еще вы можете сказать об этом уравнении?
- Оно полное и приведенное.
А какие еще виды квадратных уравнений вам известны?
Отвечают
Хорошо.
Теперь давайте проверим, насколько хорошо вы умеете определять виды квадратных уравнений. Вашему вниманию предлагается тест, в котором записаны, пять уравнений. Напротив каждой колонки вы ставите плюс, если оно принадлежит к данному виду.
Тест “Виды квадратных уравнений”
| Ф.И. | полное | неполное | приведенное | Общий балл |
| 1. х4 + 5х2 +3 = 0 | | | | |
| 2. 6х2 + 9 = 0 | | | | |
| 3. х2 – 3х = 0 | | | | |
| 4. –х2 + 2х +4 = 0 | | | | |
| 5. 3х + 6х2 + 7 =0 | | | | |
Ребята выполняют работу, а затем меняются листочками и по ключу проверяют ответы, оценивая работу товарища. Результат записывается в колонку “Оценочный балл”, а затем в “Карту результативности”( максимально 5 баллов).
Ключ к тесту:
| 1 | + | | + |
| 2 | | + | |
| 3 | | + | + |
| 4 | + | | |
| 5 | + | | |
М
Карточка:
Выбери из представленных в задании уравнений те, которые являются квадратными:
- 12х2-0,3=(0,4х2-2)30 6. 6х-8=х(1,5+2х)
- 3х2=0 7. х2=0
- (х-3)(х-5)=2х 8. х(х-2,6)(х-1)=0
-
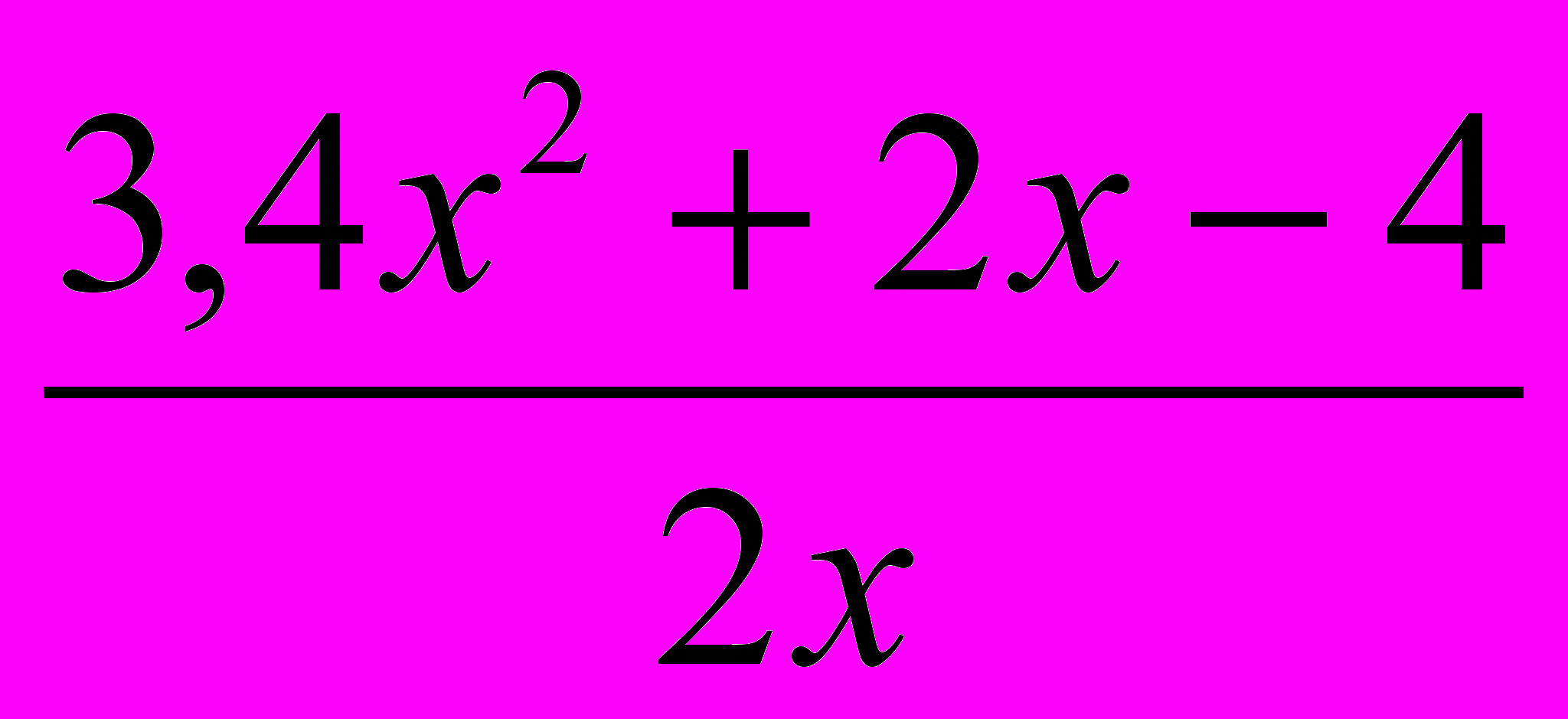=0 9.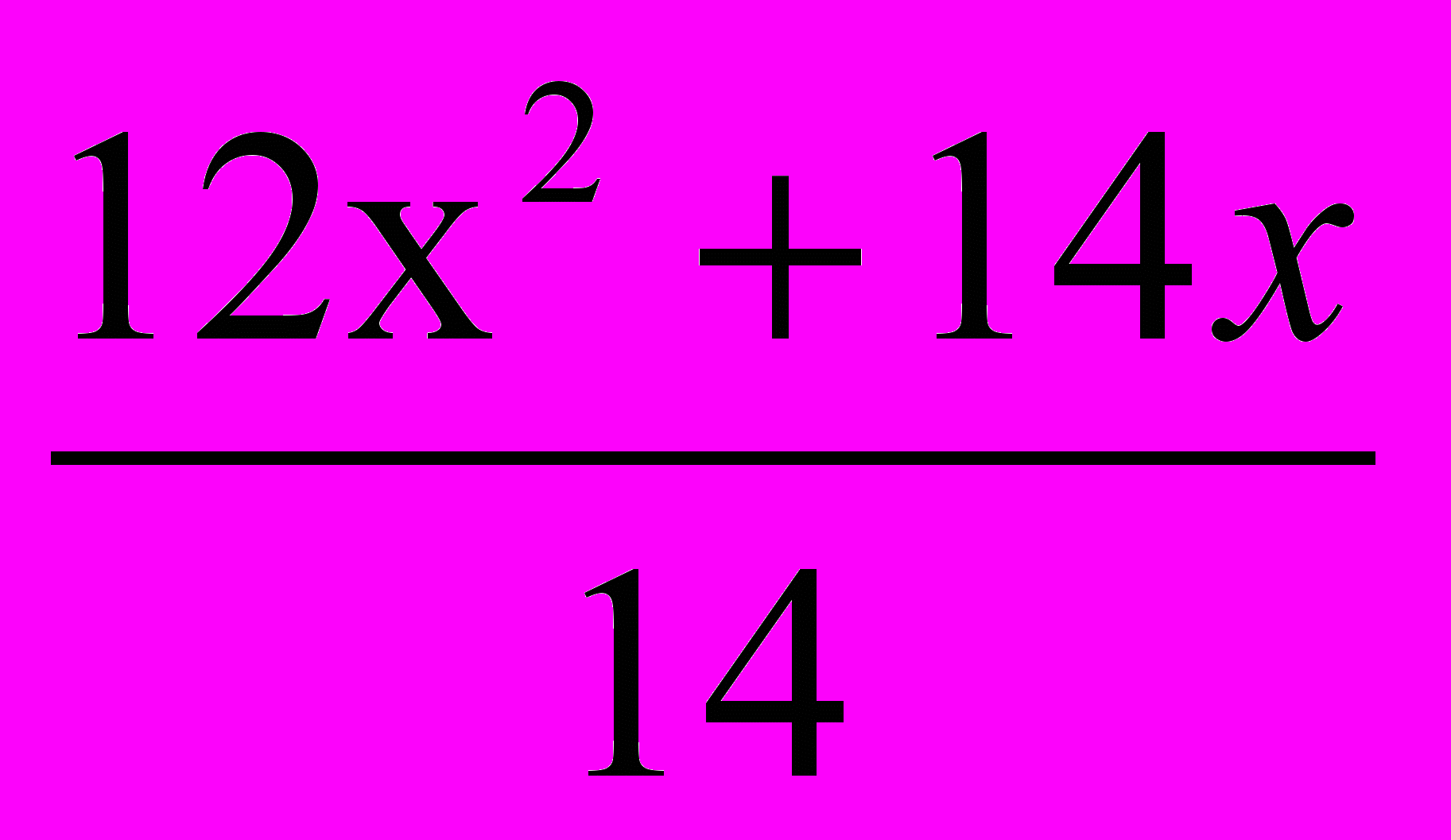 
-2,8х=14,7
-
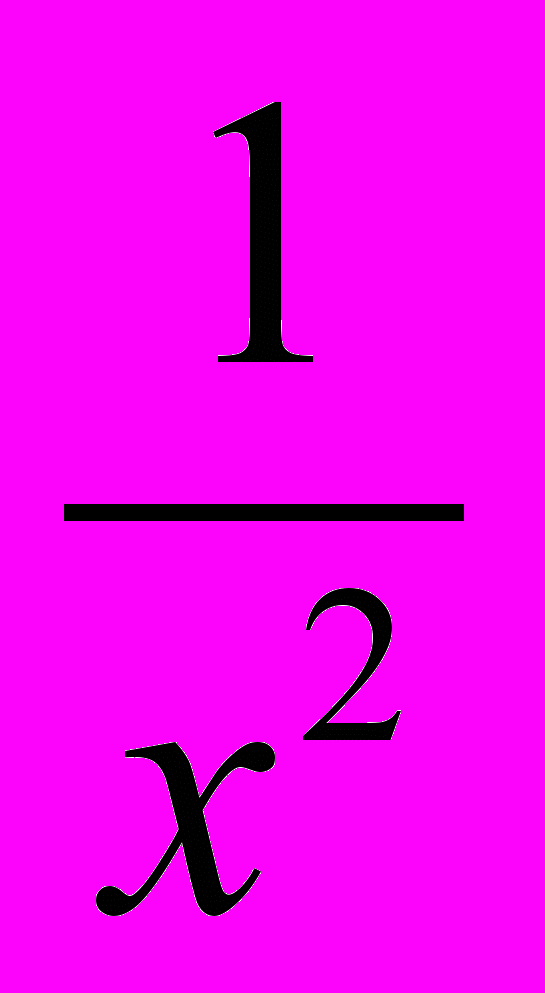+48х=х2-10 10. 8х4-2,3х2+10=0
олодцы. С видами квадратных уравнений мы разобрались. Кстати, а вы знаете, когда появились первые квадратные уравнения?
Очень давно. Их решали в Вавилоне около 2000 лет до нашей эры, а Европа три года назад отпраздновала 800летие квадратных уравнений, потому что именно в 1202 году итальянский ученый Леонард Фибоначчи изложил формулы квадратного уравнения. И лишь в 17 веке, благодаря Ньютону, Декарту и другим ученым эти формулы приняли современный вид.
А с каким еще понятием мы постоянно сталкиваемся при решении квадратных уравнений?
С дискриминантом
А вот понятие Д придумал английский ученый Сильвестр, он называл себя даже “математическим Адамом” за множество придуманных терминов. А зачем он нам нужен?
Он определяет число корней квадратного уравнения.
И как количество корней зависит от Д?
Дети перечисляют случаи.
Итак, давайте еще раз проговорим алгоритм решения полного квадратного уравнения.
Проговаривают.
Ну что ж, приступим к практической части нашего урока.
Чтобы решить уравнение,
Корни его отыскать.
Нужно немного терпения,
Ручку, перо и тетрадь.
Перед вами список различных уравнений. Посмотрите внимательно на уравнения 1-3 и скажите: являются ли эти уравнения квадратными?
Да. Потому что наивысшая степень 2.
А что нас смущает во внешнем виде этих уравнений?
Они записаны не в стандартном виде.
Итак, преобразуйте данные уравнения к стандартному виду (3 балла).
| 1. х + 5х2 = 6 | 5х2 + х - 6 = 0 |
| 2. 4х – 5 + x2 = 0 | х2 + 4х - 5 = 0 |
| 3. (2 - 5х)2 = 9 | 25х2 – 20х – 5 = 0 |
А каким методом решаются следующие два уравнения?
Метод введения новой переменной.
Вспомним, как решаются такие уравнения, поработаем вместе у доски.
| 4. х4 + 7х2 – 8 = 0 | х =-1; х = 1 |
| 5. (1 – y2)2 + 7(1 – y2) + 12 = 0 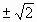| х =  ; х = |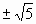
Хорошо. Вместе мы поработали. Теперь посмотрим, как вы умеете работать самостоятельно. Вам предлагается трехуровневая работа. Если вы еще не уверены в своих силах и желаете закрепить решение уравнение, то выбираете уровень А(6 балла) .Если считаете, что материал усвоен хорошо – В (9 баллов). Ну, а если желаете испробовать свои силы на более сложных заданиях – уровень С (12 баллов)для вас. В процессе решения я проверяю ваши работы и проставляю заработанные баллы.
Вариант 1.
Уровень А
№1. Для каждого уравнения вида ax2 + bx + c = 0 укажите значения a, b, c.
а) 3х2 + 6х – 6 = 0, б) х2 - 4х + 4 = 0
№2. Продолжите вычисление дискриминанта D квадратного уравнения ax2 + bx + c = 0 по формуле D = b2 - 4ac.
5х2 - 7х + 2 = 0, D = b2 - 4ac = (-7)2 – 4· 5 · 2 = …;
№3. Закончите решение уравнения 3х2 - 5х – 2 = 0.
D = b2 - 4ac = (-5)2- 4· 3·(-2) = 49; х1 = … х2=…
Уровень В Решите уравнение: а) 6х2 – 4х + 32 = 0; б) х2 + 5х - 6 = 0.
Уровень С
Решите уравнение: а) -5х2 – 4х + 28 = 0; б) 2х2–8х–2=0. x1=2+
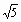, x2=2–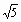Доп. задание. При каком значении а уравнение х2 - 2ах + 3 = 0 имеет один корень?
Вариант 2.
Уровень А
№1. Для каждого уравнения вида ax2 + bx + c = 0 укажите значения a, b, c.
а) 4х2 - 8х + 6 = 0, б) х2 + 2х - 4 = 0
№2. Продолжите вычисление дискриминанта D квадратного уравнения ax2 + bx + c = 0 по формуле D = b2 - 4ac.
5х2 + 8х - 4 = 0, D = b2 - 4ac = 82 – 4· 5 · (- 4) = …;
№3. Закончите решение уравнения х2 - 6х + 5 = 0.
D = b2 - 4ac = (-6 )2 - 4· 1·5 = 16; х1 = … х2=…
Уровень В Решите уравнение: а) 3х2 – 2х + 16 = 0; б) 3х2 - 5х + 2 = 0.
Уровень С
Решите уравнение: а) 5х2 + 4х - 28 = 0; б) х2 – 6х + 7 = 0; x1=3+
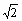, x2=3–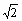.Доп.задание. При каком значении а уравнение х2 + 3ах + а = 0 имеет один корень.
IV. Подведение итогов.
Итак, мы проделали большую работу. Повторили всю теорию, касающуюся полных квадратных уравнений. Прорешали различные их виды как вместе, так и вы сами. Вы старательно зарабатывали баллы, настало время подвести итог.
Подсчитайте сумму баллов заработанных в течение урока.
Критерии оценивания:
25 – 30 баллов – “12”.
19 – 24 баллов – “9”.
10 -18 баллов – “6”.
Выставляются оценки.
Да, кстати, у меня для вас есть еще один сюрприз, который я спрятала в классе. Для того, чтобы узнать, где он находится надо решить следующее задание:
В уравнении х2 – рх + 3 = 0 один из корней равен 9. Если вы найдете число р, то узнаете номер парты, а второй корень укажет ряд, на котором находится парта с сюрпризом.
Сюрпризом будет конвертик со следующей надписью:
Франсуа Виет
Жизнь Виета представляет для нас интерес во многих отношениях.
XV век в Западной Европе был веком ожесточенных религиозных волнений, и к началу XVI целый ряд стран отпал от католической церкви.
Всесильная католическая церковь преследовала и убивала всякую мысль, в которой усматривала отклонение от своих учений. Церковный суд – инквизиция – всех попавшихся под подозрение карал вплоть до сожжения на костре, а имущество казненных отбирал в пользу церкви. Не один ученый погиб в руках инквизиции. В их числе были и математики.
Испанский математик Вальмес в 1486 году как-то в семейном кругу обмолвился о том, что нашел формулу для решения уравнения четвертой степени. В числе гостей оказался влиятельный инквизитор. Услышав слова Вальмеса, он заявил, что волей Божьей решать эти уравнения человеку не дано, а найти формулу можно было только с помощью дьявола.
В ту же ночь Вальмес был брошен в тюрьму, а через три недели сожжен на костре за связь с дьяволом. Лишь через 100 лет решение этих уравнений было найдено вторично.
Мэтр Виет также был на волосок от костра.
В ту пору наиболее могущественное государство в Европе, Испания вела победоносную войну с Францией.
Однажды французам удалось перехватить приказы испанского правительства командованию своих войск, написанные очень сложным шифром (тайнописью). Виет с помощью математики сумел найти ключ к этому шифру. С этих пор французы, зная планы испанцев, с успехом предупреждали их наступления.
Инквизиция обвинила Виета в том, что он прибегнул к помощи дьявола, и приговорила к сожжению на костре. Но так как французы благодаря Виету в дальнейшем побеждали, он не был выдан инквизиции.
В родном городке Виет был лучшим адвокатом, а позднее стал королевским советником. Но главным делом его жизни была математика. Биографы Виета пишут, что он мог несколько ночей подряд не спать, решая очередную математическую задачу.
- Домашнее задание.
- Подготовка к контрольной работе.
- Разноуровневое домашнее задание.
| 9 баллов | 12 баллов |
| Решить уравнения: 1)15х2-4х-3=0; 2)х2-7х+4=0; 3)х2+5х+9=0. | Решить уравнения: 1)х2-20х+91=0; 2)(3х-1)(3х+1)-2х(1+4х)=-2; 3)(3х+1)2-х(7х+5)=4. |
| Составить квадратное уравнение, если его корни равны: х1=-2.5; х2=2. | Составить квадратное уравнение, если его корни равны: х1= 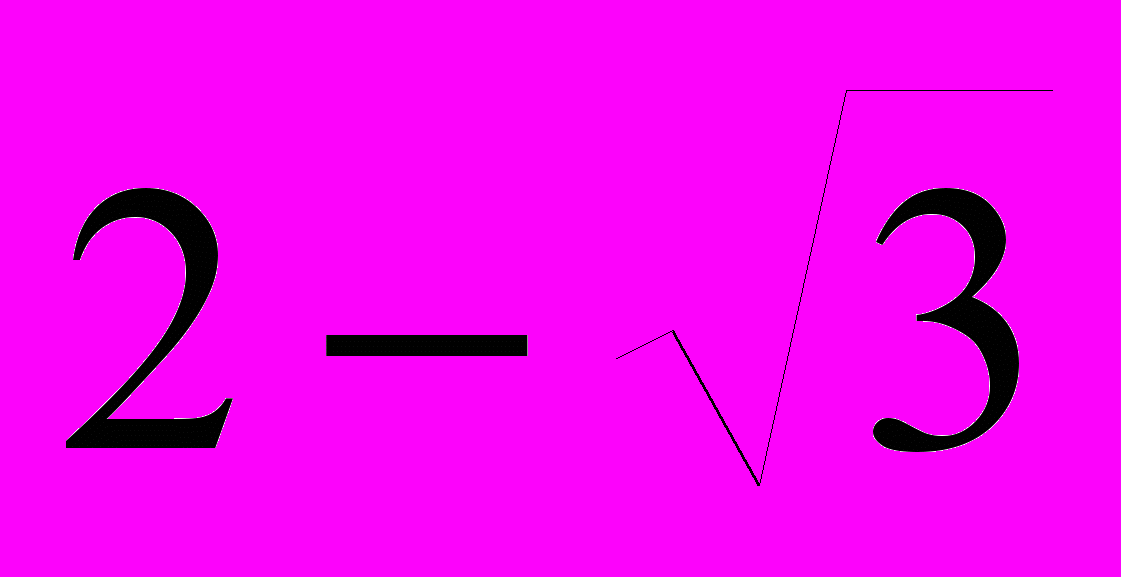 х2=  |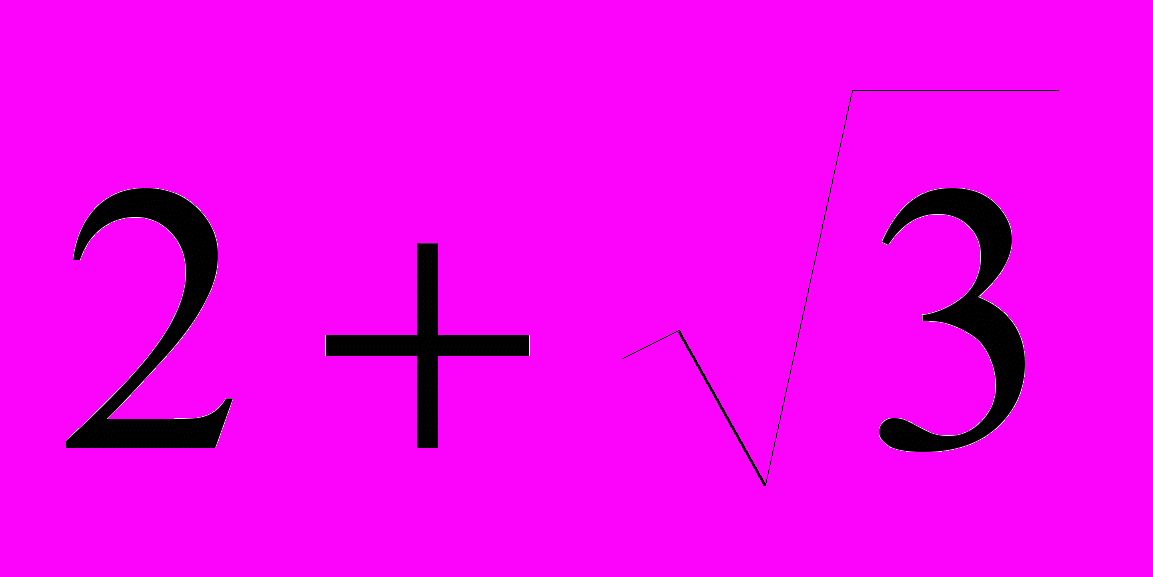
| В уравнении х2+рх-12=0 один из корней равен 4. Найдите второй корень и число р. | В уравнении (а-7)х2-13х-а=0 один из корней равен 5. Найдите число а и второй корень уравнения. |
УРОК №8
Тема: Контрольная работа по теме «Квадратные уравнения. Формула корней квадратного уравнения. Теорема Виета.»
Цель:
- Проверить уровень усвоения данной темы и уровень умений и навыков, сформированный по данной теме.
- Развитие самоконтроля и самопроверки.
- Воспитание трудолюбия и ответственности за выполнение работы.
Тип урока: Урок контроля знаний и умений.
Ход урока.
- Организационный этап.
- Тема и цель урока.
- Условие контрольной работы.
Вариант №1
1 ЧАСТЬ.
- Вычислите дискриминант уравнения: 2х2+3х+1=0
А) 11 Б)17 В)-5 Г)1
2) Решите уравнение: х2+5х=0
А)0;5 Б)-5;0 В)-5 Г)5
3)Выпиши коэффициенты квадратного уравнения: 5х2-9х+4=0
А) 5,-9,-4 Б)5,9,4. В)5,-9,4 Г)-5, -9, -4
4) реши уравнение х2-6х+8=0
А)2,4 Б)решение нет В)-4;-2 Г)другой ответ
5)Не решая уравнения найдите сумму и произведение корней уравнения х2+5х-24=0
А) 5;24 Б) 5;-24 В)-5;-24 Г)-5;24
6)реши уравнение (у-6)(у+8)=-48
А) 2;0 Б)-2 В)0 Г) решений нет
- ЧАСТЬ
1)х4-5х2-36=0
2)при каком значении k уравнение имеет только один корень : 2х2+4х+ k=0
3 ЧАСТЬ
1)(х2-2)2+3(х2-2)+2=0
2) (2х-1)(2х+1)-(х-3)(х+1)=18
Вариант №2
- ЧАСТЬ.
1)Вычислите дискриминант уравнения: 2х2+5х+2=0
А)41 Б)9 В)-11 Г)21
2) Решите уравнение: х2+3х=0
А)0;3 Б)-3;0 В)-3 Г)3
3)Выпиши коэффициенты квадратного уравнения: 3х2-5х-2=0
А) -3,-5,-2 Б)3,5,-2. В)3,-5,2 Г)3,-5,-2
4) реши уравнение х2-4х+6=0
А)-3,-2 Б)-1,6 В)2,3 Г)другой ответ
5)Не решая уравнения найдите сумму и произведение корней уравнения х2+5х-14=0
А) 5;-14 Б) 5;14 В)-5;-14 Г)-5;14
6)реши уравнение (у+5)(у-9)=-45
А) 4;0 Б)4 В)0 Г) решений нет
- ЧАСТЬ
1)х4-6х2+8=0
2)при каком значении k уравнение имеет только один корень : 2х2 -6х+ k=0
3 ЧАСТЬ
1)(х2+3)2-7(х2+3)+12=0
2) (3х-1)(3х+1)-(х+2)(х-1)=8
- Итоги урока.
Решение задание, которые вызвали трудности при решении.
- Домашнее задание.
Повторить : определение многочлена, разложение многочленов на множитель, основные свойства дробей, сокращение дробей.
Автор: Любимченко О.В., вчитель математики, Торезька гімназія суспільно-гуманітарного профілю Донецької області