Урок №1 Тема : Определение квадратного уравнения. Неполные квадратные уравнения и их решения
| Вид материала | Урок |
- Урок-лекция по теме «Определение квадратного уравнения. Неполные квадратные уравнения.», 43.99kb.
- Урок по алгебре в 8-м классе по теме: «Определение квадратного уравнения. Неполные, 70.52kb.
- А Квадратные уравнения в Древнем Вавилоне, 58.12kb.
- Методические разработки по теме, модулю, разделу преподаваемого предмета». Тема: «Квадратные, 420.13kb.
- Задачи данного элективного курса заключаются в следующем: предоставить возможность, 63.74kb.
- Тема урока: «Дробные рациональные уравнения», 93.81kb.
- Вопросы к экзамену по учебной дисциплине «Дифференциальные уравнения», 32.43kb.
- Тема: Уравнение с двумя переменными. Цели урока, 251.03kb.
- Синявская средняя общеобразовательная школа, 63.47kb.
- Урок в 8 классе ( русский язык и математика) Тема: «Вместе будем обобщать», 71.21kb.
Цели урока:
- Ознакомить учащихся с теоремой Виета и ее доказательством.
- Научить применять теорему Виета при решении уравнений,
- Развить интерес к предмету через игровые формы работы.
Тип урока: Овладение новыми знаниями и умениями.
Ход урока
- Тема и цели урока.
II. Проверка усвоения предыдущей темы;
Фронтальный опрос.
- Какое уравнение называется квадратным?
- Какие виды квадратных уравнений вы знаете?
- Какое уравнение называется неполным квадратным?
- Какое уравнение называется приведенным?
- Что значит - решить уравнение?
- Сколько корней может иметь квадратное уравнение?
- От чего зависит количество корней квадратного уравнения?
- Как зависит?
- Какое выражение называют дискриминантом?
Теперь решим устные упражнения, которые даны на доске. В это время три ученика выйдут к доске и будут, решать следующие уравнения.
Х2+6х-7=0, (1)
Х2+7х-18=0, (2)
4х2+7х+3=0. (3)
Устные упражнения.
Укажите в квадратном уравнении его коэффициенты
3у2-5у+1=0,
12х-7х2+4=0
-х2+х-3=0,
Х2-7=0.
Замените уравнение равносильным ему приведенным уравнением.
3х2-6х-12=0,
2у2+у-7=0
1/2х2-3х+1,5=0.
Сколько корней имеет квадратное уравнение?
Х2-64=0,
У2+49=0,
2р2-7р=0,
Х2=0.
III. Объяснение новой темы.
Теперь вы должны отгадать зашифрованное слово – игра дешифровщик. Класс делится на две группы. Группы соревнуются, кто быстрее расшифрует слово.
Расшифровывается слово “Франсуа Виет”.
Это имя великого французского математика. С этим именем связанна тема этого урока. Франсуа Виет – французский математик, живший в 16 веке. Он родился в 1540 году в небольшом городке на юге Франции. Он обладал огромной трудоспособностью, мог работать по трое суток без отдыха. Он был одним из первых, кто ввел систему алгебраических символов, разработал основы элементарной алгебры. Многие его результаты и открытия достойны восхищения. Свою знаменитую теорему, которую мы рассмотрим сегодня, он доказал в 1591 году. Это теорема выражает интересную закономерность, существующую между суммой корней квадратного уравнения и его коэффициентами, между произведением корней квадратного уравнения и его коэффициентами.
Чтобы увидеть эту закономерность, обратимся к уравнению (1), которое решено на доске первым учеником. Чему равна сумма корней.
Х1+х2= -7+1= -6
Давайте, сравним это число с коэффициентами уравнения! Вы видите, что оно равно второму коэффициенту уравнения 1,взятому с противоположным знаком.
Посмотрим, чему равно произведение корней?
Х1*х2= -7*1= -7
С каким коэффициентом уравнения его удобно сравнить?
Какой вывод можно сделать?
Теперь найдем сумму корней и произведение корней уравнения (2), которое решено на доске вторым учеником, и сравним эти числа с коэффициентами уравнения.
Вывод:
Теорема. Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Формулировка теоремы повторяется учениками.
Доказательство.
Пусть X1 и X2 – корни квадратного уравнения x2+px+g=0
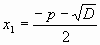 ;
; 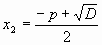 ;
;Найдем,
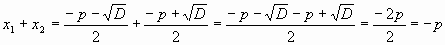
Найдем,
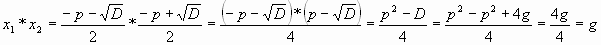
Уравнение 3 не приведенное, поэтому, для нее эта закономерность не выполняется. Но если уравнение заменить равносильным ему приведенным, то можно увидеть, что
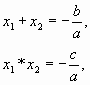
Теореме Виета посвящены такие строки:
По праву достойна в стихах быть воспета
О свойстве корней Теорема Виета.
Что лучше, скажи, постоянства такого?
Умножишь ты корни и дробь уж готова
В числителе “С”, в знаменателе “А”.
А сумма корней тоже дроби равна
Хоть с минусом дробь – это что за беда?
В числителе “В”, в знаменателе “А”.
IV. Закрепление темы.
Теперь посмотрим, для чего нужна эта теорема, так ли она важна.
Упражнение 1. Найдем сумму и произведение корней квадратного уравнения, не решая его.
Х2-37х+27=0
2х2-9х-10=0
5х2-12х+7=0
К доске вызываются ученики для решения этого упражнения. Чем можно воспользоваться для нахождения суммы и разности корней?
Упражнение 2. Найдем подбором кони уравнения.
Х2-9х+20=0
х2+11х-12=0
Упражнение 3. Составим уравнение, корнями которого являются числа -2 и 5.
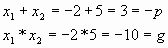
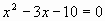
Самостоятельно составить уравнение, корнями которого являются числа 3 и 7.
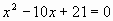
Теперь скажите, можно ли решить эти задания, не зная теоремы Виета? Нужна ли эта теорема?
Дополнительные задания.
1) В каком из этих уравнений сумма корней равна -6,
а произведение корней равно - 16?
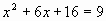
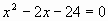
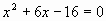
2) №1009, 1010, 1012,1015
V. Подведение итогов урока.
Выполнение компьютерного теста.
Запишите приведенное квадратное уравнение, в котором второй коэффициент и свободный член равны соответственно:
1. -5 и 4. 2. 3 и -2.
А)х2-5х+4=0; Б)х2+5х+4=0; А)х2-Зх-2=0; Б) х2+Зх-2=0;
В) х2-5х-4=0; Г)-х2-5х+4=0. В)х2+Зх+2=0; Г)-х2+Зх-2=0.
3. -2 и 2,5. 4.-3 и 9,6.
А) -х2-2х-2,5=0; Б) х2+2х+2,5=0; А)х2-3х+9,6=0; Б) 5х2+31х+48=0;
В) х2-2х+2,5=0; Г) інша відповідь. В) х2-6,2х+9,6=0; Г) інша відповідь.
Не решая уравнения, найдите сумму и произведение его корней:
1.х2-3х-10=0. 2. х2-5х-14=0.
А)-3;-10; Б)3;-10; А) 5;-14; Б)-5;-14;
В)-3;10; Г)3;10. В) 5;14; Г)-5;14.
3. х2+5х-24=0. 4.х2-19х+6=0.
А)5;24; Б) 5;-24; А)6;-19; Б)-6;19;
В) -5;24; Г) -5;-24. В) 19;6; Г) -6;19.
Составьте квадратное уравнение, которое имеет корни:
1. 1 и 3. 2. 2 и 5.
А)х2-4х+3=0; Б)х2-Зх+4=0; А)х2-7х-10=0; Б)х2+7х+10=0;
В) х2+Зх-4=0; Г)х2+4х-3=0. В)х2-7х+10=0; Г) інша відповідь.
3. 2 и 7. 4.3 и 4.
А)х2+9х+14=0; Б)х2-9х+14=0; А) х2-7х+12=0; Б)х2+Зх+4=0;
В)х2-9х-14=0; Г) інша відповідь. В) 4х2+3х=0; Г)х2-х-12=0.
VI. Домашнее задание.
Параграф 21
№ 1011,1013,1016,1017.
Подготовить рефераты по теме «Виет – великий математик»
УРОК №6
Тема: Теорема Виета
Цели урока:
- применять теорему Виета к решению задач;
- решать приведенные квадратные уравнения по теореме, обратной теореме Виета;
- ставить и решать проблемы;
- анализировать данные и результаты;
- формулировать выводы;
- работать в группе;
- развивать логическое мышление.
- воспитывать трудолюбие, развивать самостоятельность.
Тип урока: закрепление знаний и умений.
Ход урока
- Тема и цель урока.
Учащиеся формулируют цели и задачи урока.
- Проверка домашнего задания
Самопроверка по образцу, который был написан заранее на доске одним из учеников.
- Актуализация опорных знаний.
На протяжении последних уроков мы занимались решением квадратных уравнений.
- Уравнение какого вида называется квадратным?
- Как называется квадратное уравнение, первый коэффициент которого равен 1? (Заслушиваются ответы учащихся).
- Какие методы решения квадратных уравнений вы знаете? (Учащиеся называют известные им способы решения).
- Решение упражнений.
Решите каждое квадратное уравнение известным вам способом.
Заполните рабочий лист.
Рабочий лист
| 1 | 2 | 3 | 4 | 5 | 6 |
| Приведенное квадратное уравнение х2 + px + q = 0 | Второй коэффициент p | Свободный член q | Корни х1 и х2 | Сумма корней х1 + х2 | Произведение корней х1 · х2 |
| х2 + 7х + 12 = 0 | 7 | 12 | -3 и -4 | -7 | 12 |
| х2 - 9х + 20 = 0 | -9 | 20 | 4 и 5 | 9 | 20 |
| х2 – х - 6 = 0 | -1 | -6 | -2 и 3 | 1 | -6 |
| х2 + х – 12 = 0 | 1 | -12 | -4 и 3 | -1 | -12 |
| х2 + х + 30 = 0 | 1 | 30 | нет | - | - |
Задание №1 (работа в группах)
Задания для исследования каждой группе
| 1 группа х2 + 7х + 12 = 0 х2 - 10х + 21 = 0 х2 – 3х – 10 = 0 х2 +3х – 10 = 0 х2 + 3х + 10 = 0 | 2 группа х2 + 5х + 6 = 0 х2 - 9х + 20 = 0 х2 – 2х – 15 = 0 х2 + 2х – 15 = 0 х2 + 2х + 15 = 0 | З группа х2 + 7х + 10 = 0 х2 - 8х + 15 = 0 х2 – х – 6 = 0 х2 + х – 6 = 0 х2 + х + 6 = 0 |
| 4 группа х2 + 8х + 15 = 0 х2 - 7х + 10 = 0 х2 – х – 12 = 0 х2 + х – 12 = 0 х2 + х + 12 = 0 | 5 группа х2 + 10х + 21 = 0 х2 - 7х + 12 = 0 х2 – х – 30 = 0 х2 + х – 30 = 0 х2 + х + 30 = 0 | 6 группа х2 + 9х + 20 = 0 х2 - 11х + 30 = 0 х2 – 5х – 14 = 0 х2 + 5x – 14 = 0 х2 + 5х + 14 = 0 |
Выпишите на чистом листе пять пар чисел, являющихся корнями квадратных уравнений, которые вы решали на этапе исследования.
Обменяйтесь этими листами с соседними группами.
По заданным корням составьте соответствующие им квадратные уравнения.
Дайте эти уравнения на проверку группе, которая готовила вам задание.
Осуществляется проверка правильности выполнения задания каждой группой по пятибалльной шкале.
- Как вы считаете, какая теорема позволяет определять знаки корней квадратного уравнения (если эти корни существуют)?
- Верно, прямая теорема.
Задание №2 (работа в группах)
1. Не решая уравнение, определите знаки его корней:
1) х2 + 45х – 364 = 0 – для первой группы;
2) х2 + 36х + 315 = 0 – для второй группы;
3) х2 – 40х + 364 = 0 – для третьей группы;
4) х2 – 30х + 250 = 0 – для четвертой группы.
2. Не применяя формулу корней, найдите второй корень уравнения, если известен первый:
1) х2 + 45х – 364 = 0, х1 = 7 – для пятой группы;
2) х2 – 40х + 364 = 0, х1 =14 – для шестой группы.
Проверяется правильность выполнения задания каждой группой (верно выполненное задание – 2 балла).
Математиков всегда интересовал вопрос, как решить задачу более рациональным способом.
- Нельзя ли находить корни приведенного квадратного уравнения методом подбора?
- Какую теорему в этом случае будем использовать? (Для нахождения корней приведенного квадратного уравнения методом подбора используется теорема, обратная данной).
Образец. Решить уравнение х2 – х – 6 = 0.
Решение:
х1+ х2= 1,
х1 · х2 = -6;
по теореме, обратной данной, х1 = -2, х2 = 3.
Ответ: -2; 3
Задание №3 (индивидуальная работа)
Учащиеся самостоятельно находят методом подбора корни приведенного квадратного уравнения, причем, ученик решает уравнение, соответствующее его порядковому номеру. Ученик, справившийся с заданием, на доске под своим порядковым номером записывает букву.
Решите уравнение, соответствующее своему порядковому номеру, и выберите больший корень уравнения:
|
|
Код: большему корню уравнения соответствует буква
| -11 | -10 | -9 | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| я | к | м | ч | с | ц | г | и | н | ф | т | а | о | в | л | р | б | е | ы | п | у | т |
Если уравнения решены верно, то получится словосочетание:
| 1 2 3 4 5 6 7 | 8 9 10 11 | 12 13 14 15 | 16 17 18 19 20 21 22 |
| Ф р а н с у а | В и е т | о т е ц | а л г е б р ы |
- Как вы думаете, можно ли применять теорему Виета к неприведенному квадратному уравнению? (Да, можно).
Найдите сумму и произведение корней в следующих уравнениях:
а) 2х2 −7х + 20 = 0;
б) 3х2 + 21х + 1 = 0.
V. Домашнее задание.
Приготовьте доказательство теоремы, обратной теореме Виета, для приведенного квадратного уравнения.
Докажите теорему Виета для квадратного уравнения вида ax2 + bx + c = 0.
Составьте, решите и оформите на формате А4 три задачи на применение теоремы Виета и три задачи на применение теоремы, обратной теореме Виета.
Попробуйте сочинить стихотворение о теореме Виета.
VI этап. Рефлексия.
- Чем лично для вас был интересен этот урок?
- Какие формы работы вам понравились?
- На каком этапе урока вы испытывали затруднения?
- Где вы видите практическое применение изученной теоремы?
- Как вы думаете, над какими вопросами данной темы нам предстоит еще работать?
УРОК №7
Тема: Итоговый урок.
Цели урока:
- Обобщение и систематизация основных знаний и умений по теме, формирование умения решать квадратные уравнения;
- Развитие логического мышления, памяти, внимания, умения обобщать;
- Воспитание трудолюбия, взаимопомощи, взаимоуважения и математической культуры.
Тип урока: Обобщение и систематизация знаний и умений.
Ход урока.
