Методические разработки по теме, модулю, разделу преподаваемого предмета». Тема: «Квадратные уравнения в курсе алгебры 8 класса»

Вид материала

Методические разработки

Содержание Контрольная работа № 6 Содержание контрольной работы и методические пояснения Критерии оценок Ответ: 6 см – меньшая сторона прямоугольника

Подобный материал:

• Методические разработки по теме, модулю, разделу преподаваемого предмета Тема работы, 300.23kb.
• Задачи данного элективного курса заключаются в следующем: предоставить возможность, 63.74kb.
• А Квадратные уравнения в Древнем Вавилоне, 58.12kb.
• Методика изучения уравнений в курсе алгебры 7-9 классов Примерное содержание, 12.53kb.
• Урок по алгебре в 8-м классе по теме: «Определение квадратного уравнения. Неполные, 70.52kb.
• Урок-лекция по теме «Определение квадратного уравнения. Неполные квадратные уравнения.», 43.99kb.
• Урок №1 Тема : Определение квадратного уравнения. Неполные квадратные уравнения, 419.31kb.
• Решение задач повышенной сложности по теме: «Уравнения и системы уравнений», 141.17kb.
• Конспект урока в 8 классе по теме: «Квадратные уравнения.», 21.81kb.
• Тема 2: Квадратные уравнения, 34.25kb.

Контрольная работа № 6

по теме «Квадратные уравнения»


Пояснительная записка

Контрольная работа, предлагаемая автором УМК, не отвечает требованиям к итоговой аттестации выпускников, а именно:

• нарушается принцип вариативности;
  
• не создаются условия для проявления творческой инициативы, для осуществления рационального решения задачи;
  
• задачи, определяемые стандартами, усложнены, что не позволяет объективно продиагностировать уровень усвоения знаний.
  

Поэтому предлагаю заменить контрольную работу, предложенную автором УМК по данной теме.

Данная контрольная работа позволяет продиагностировать уровень усвоения темы (задания 1(а,б); 2(а,б,в) – задания базового уровня)

Задание 2(в) может быть выполнено двумя способами, предполагает выбор решения.

Содержание работы дает возможность выбора заданий, для выполнения контрольной работы на отметку «5».


Содержание контрольной работы и методические пояснения

1 вариант	2 вариант	Пояснение
Сколько корней имеет уравнение? (Ответ поясните) а) х2 – 2х +2 = 0; а) х2 + 5х + 3 = 0; б) 4х2 – 4х + 1 = 0. б) 3х2 – 2х + 5 = 0.		Проверяет: умение учащихся определять коэффициенты квадратного уравнения; знание формулы дискриминанта и его смысл.
Решите уравнение. а) 3х2 + 6х = 0; а) 10х2 + 5х = 0; б) 4х2 – 1 = 0; б) 6 – 6х2 = 0; в) х2 – 10х + 25 = 0. в) х2 + 6х + 9 = 0.		Проверяет умение решать неполные кв. уравнения вида ах2+ bх=0 и ах2+ с=0 Третье задание позволяет выбирать способ решения (применить формулу сокращенного умножения)
Решите уравнение. а) х2 – 8х + 7 = 0; а) х2 – 4х – 5 = 0; б) (3х + 1)(х – 2) = 6; б) (4х – 3)(4 – х) = 3 в) (х2+1)2–15=2(х2+1) в) (8–х2)2–10=9(8 – х2)		Проверяет умение решать полное кв. уравнение и уравнения к ним приводимые по различным формулам (дискриминанта и корней или формулы корней кв. уравнения с четным вторым коэффициентом, заменой переменной).
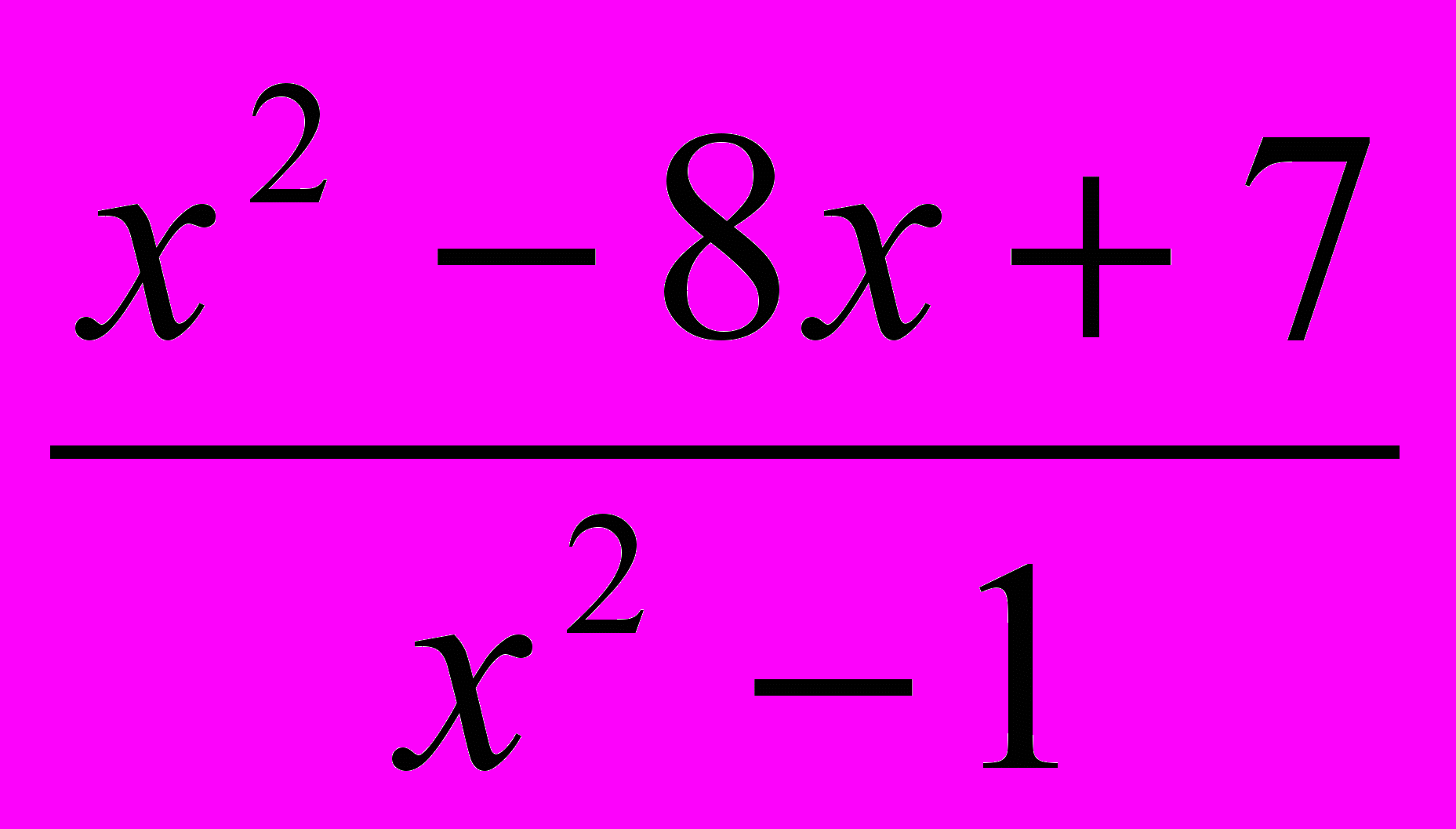Сократите дробь.		Проверяет умение раскладывать квадратный трехчлен на множители, знание правил сокращения дробей.
Найдите коэффициент k и второй корень уравнения х2 – kх – 3 =0, х2 + 6х + k = 0, если один из если один из корней корней равен 3. равен –2.		Проверяет знание теоремы Виета и умение ее применять.
Решите задачу, выделяя три этапа математического моделирования. Периметр прямо- Периметр прямоуголь- угольника равен ника равен 28 см, а его 32 см, а его пло- площадь равна 48 см2. щадь 60 см2. Найдите длину боль- Найдите длину шей стороны прямо- меньшей сторо- угольника. ны прямоуголь- ника.		Проверяет умение составлять три этапа математического моделирования.

Критерии оценок

Оценивание контрольной работы осуществляется по принципу «сложения»: оно зависит от числа заданий, которые ученик выполнил верно. При этом рекомендуется исходить из следующих критериев, проверенных на практике и учитывающих типичные ситуации, возникающие на контрольных работах.

Отметка «3» выставляется, если ученик верно выполнил1, 2 и 3(а) задание или 1, 2 + два уравнения из 3 с недочетами, или одной ошибкой.

Верное выполнение четырех заданий оценивается отметкой «4».

Отметка «5» выставляется, если ученик выполнил верно любые 5 заданий. При этом отметка не снижается, если ученик не приступил к выполнению одного из шести заданий или же допустил при его выполнении ошибку.


Решение контрольной работы.

I вариант


1. а) х² – 2х + 2= 0; б) 4х² – 4х + 1 = 0;

D=b² – 4ac D=b² – 4ac

D=(- 2)² – 4^.2= - 4 D=(- 4)² – 4^.4^.1=0

D<0 , уравнение имеет D=0, уравнение имеет

два корня один корень


2. а) 3х² + 6х =0; б) 4х² – 1 = 0; в) х² – 10х + 25 = 0

3х(х + 2)=0 4х² = 1 (х – 5)² = 0

х=0 или х + 2 =0 х² = 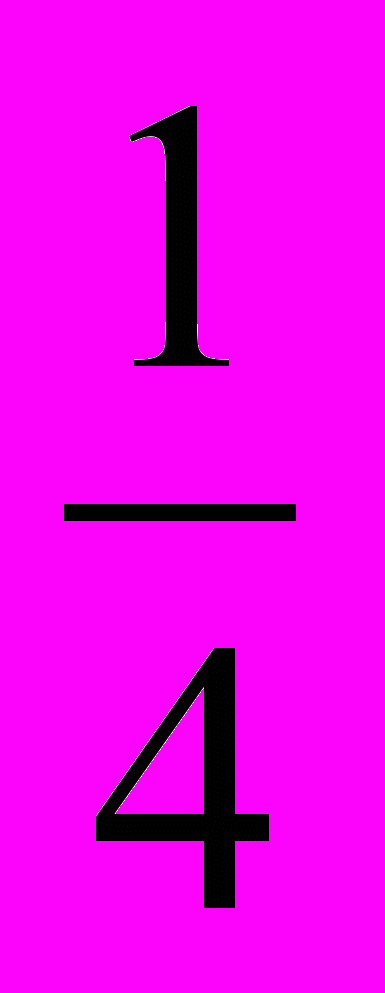х – 5 = 0

х= - 2 х = 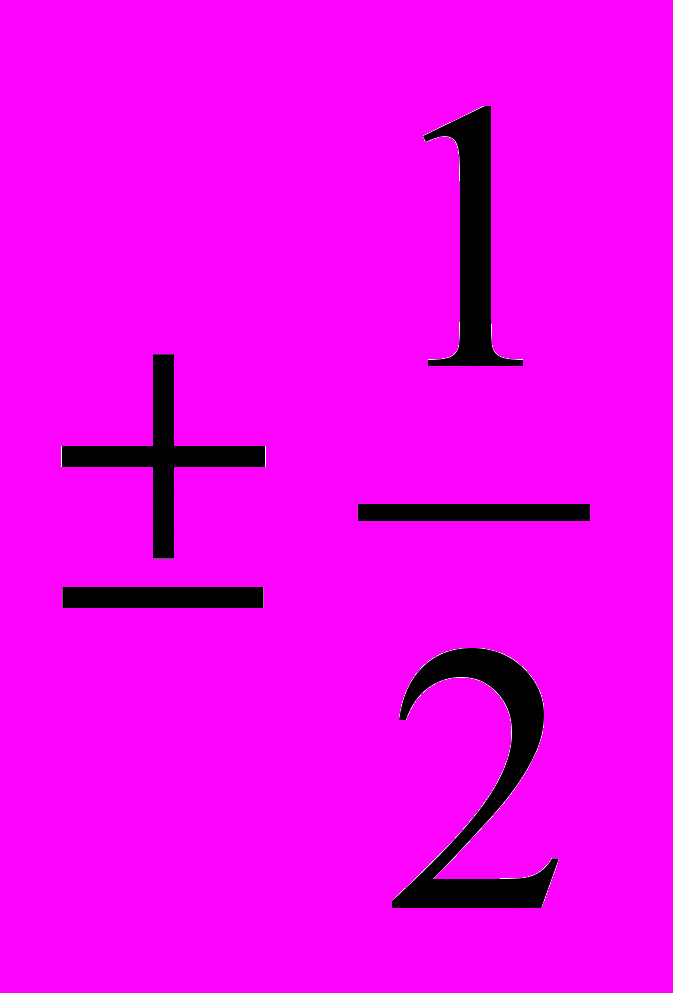х = 5


Ответ: 0; - 2. Ответ: 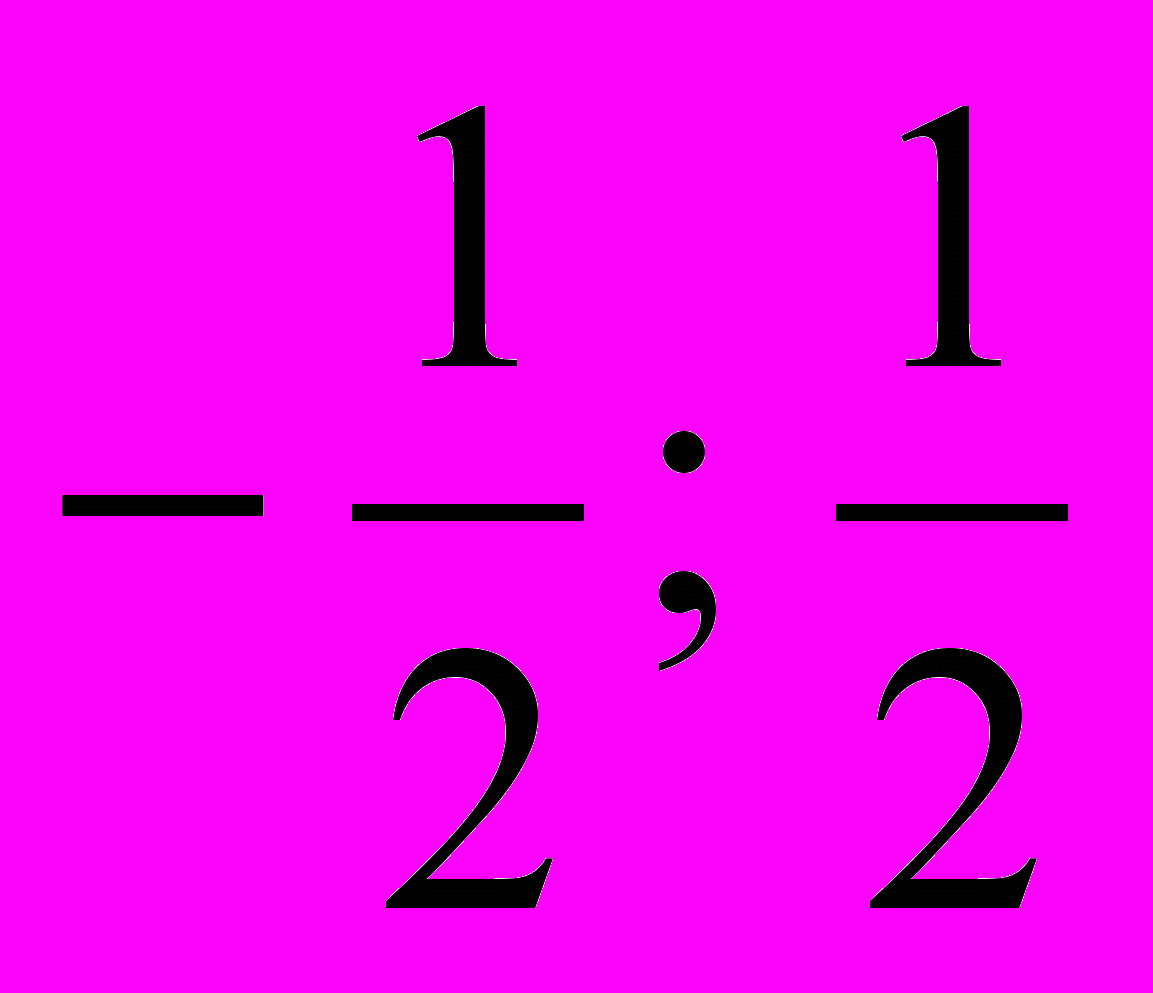Ответ: 5


3. а) х² – 8х + 7 = 0; б) (3х + 1)(х – 2) = 6

k = - 4; х_1,2 = 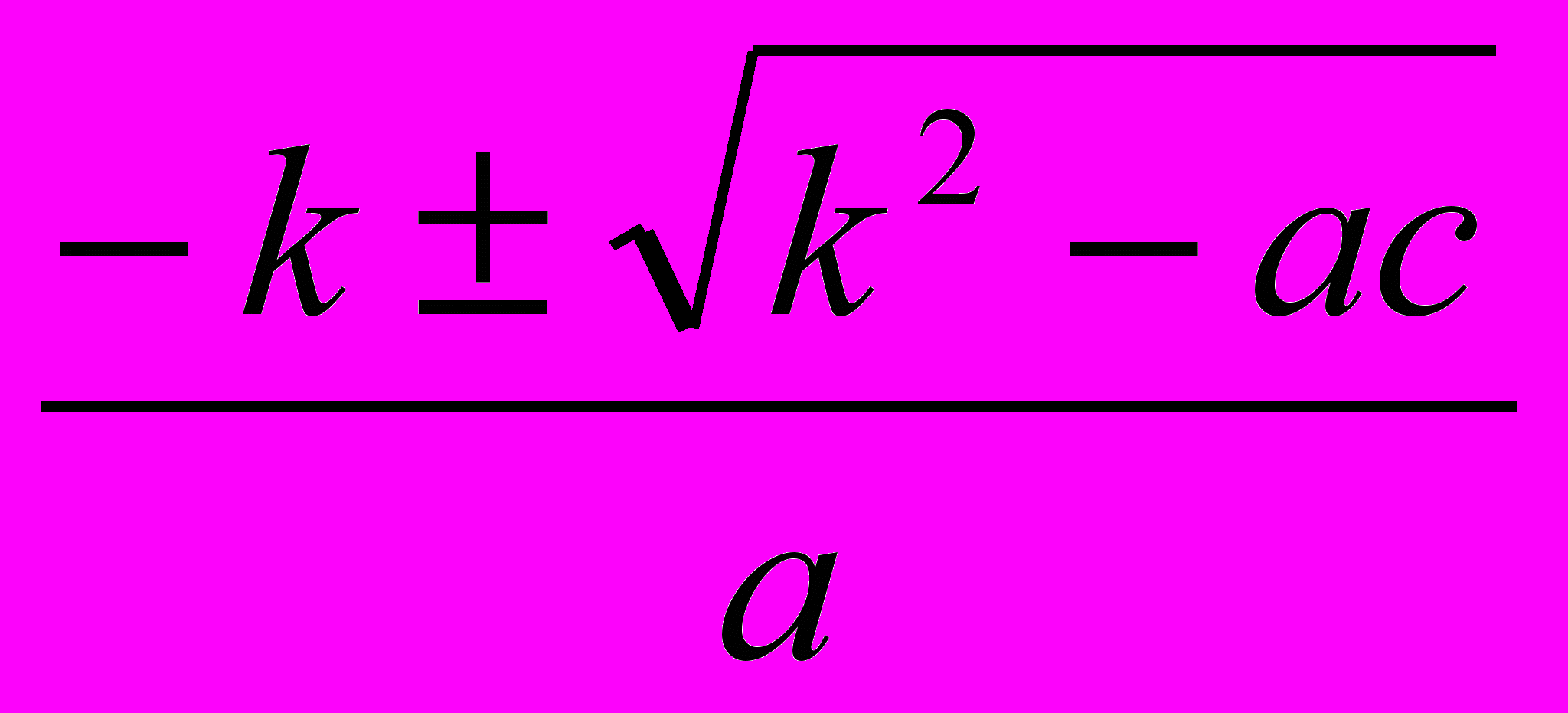3х² – 6х + х – 2 – 6 = 0

х₁ = 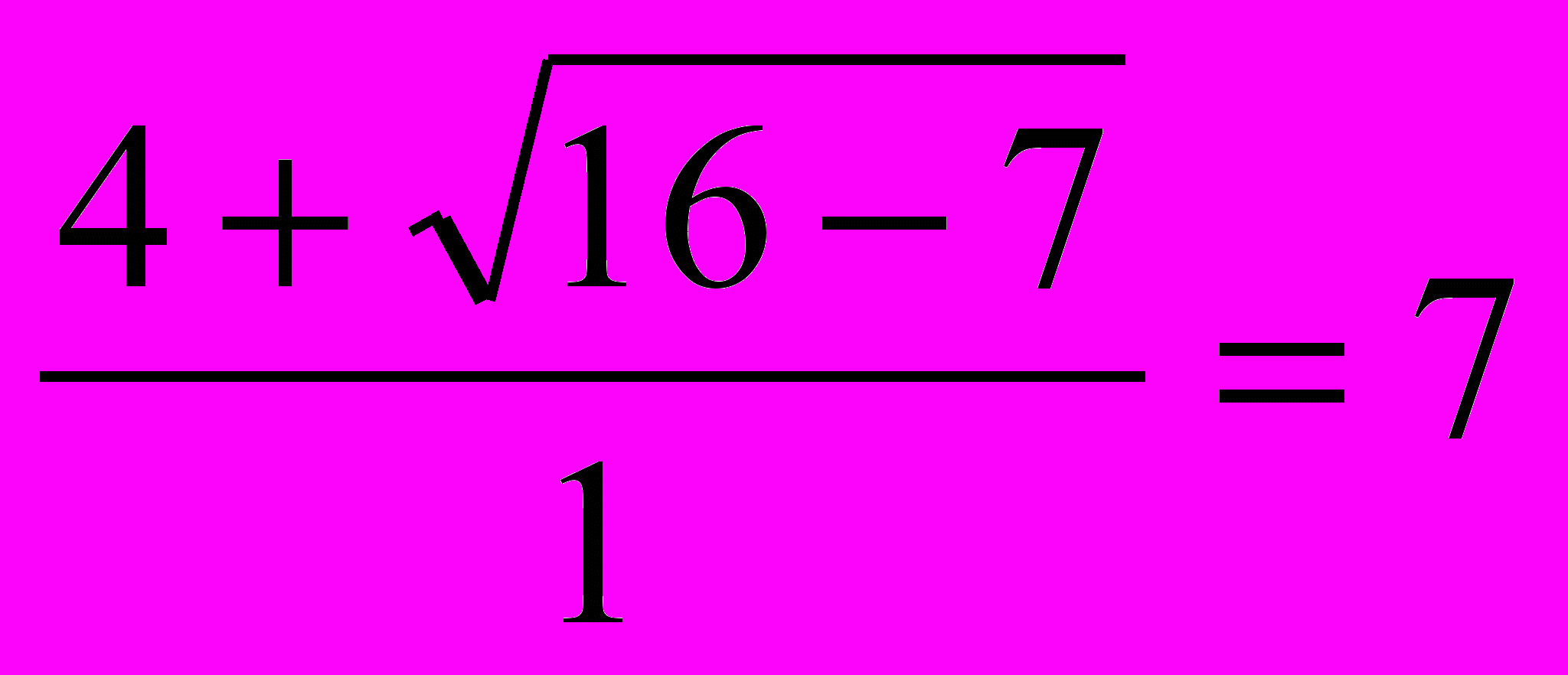3х² – 5х – 8 = 0


х₂ = 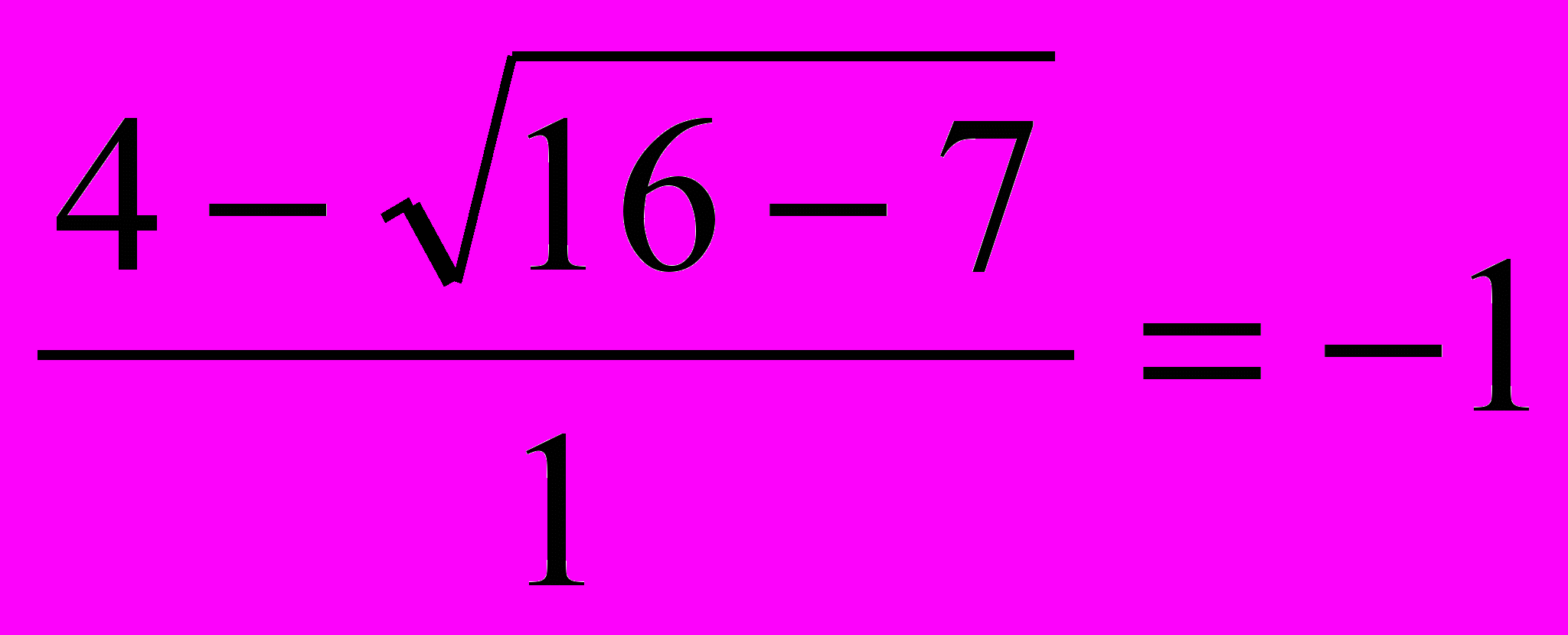D=b² – 4ac ; D=(- 6)²- 4^.3^.(- 8)

Ответ: - 1; 7 D=121; х_1,2=

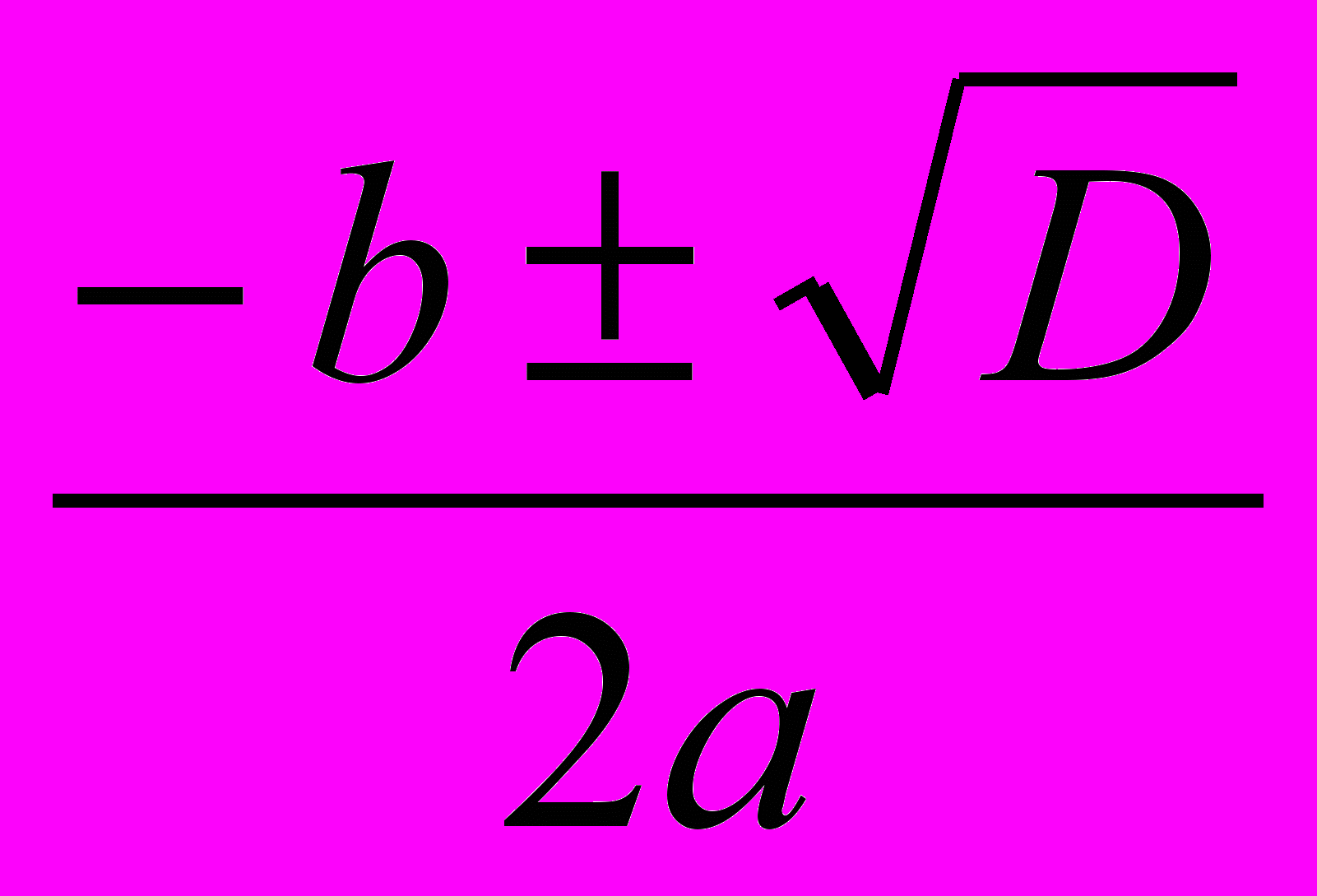
Можно решить по формуле D. х₁=

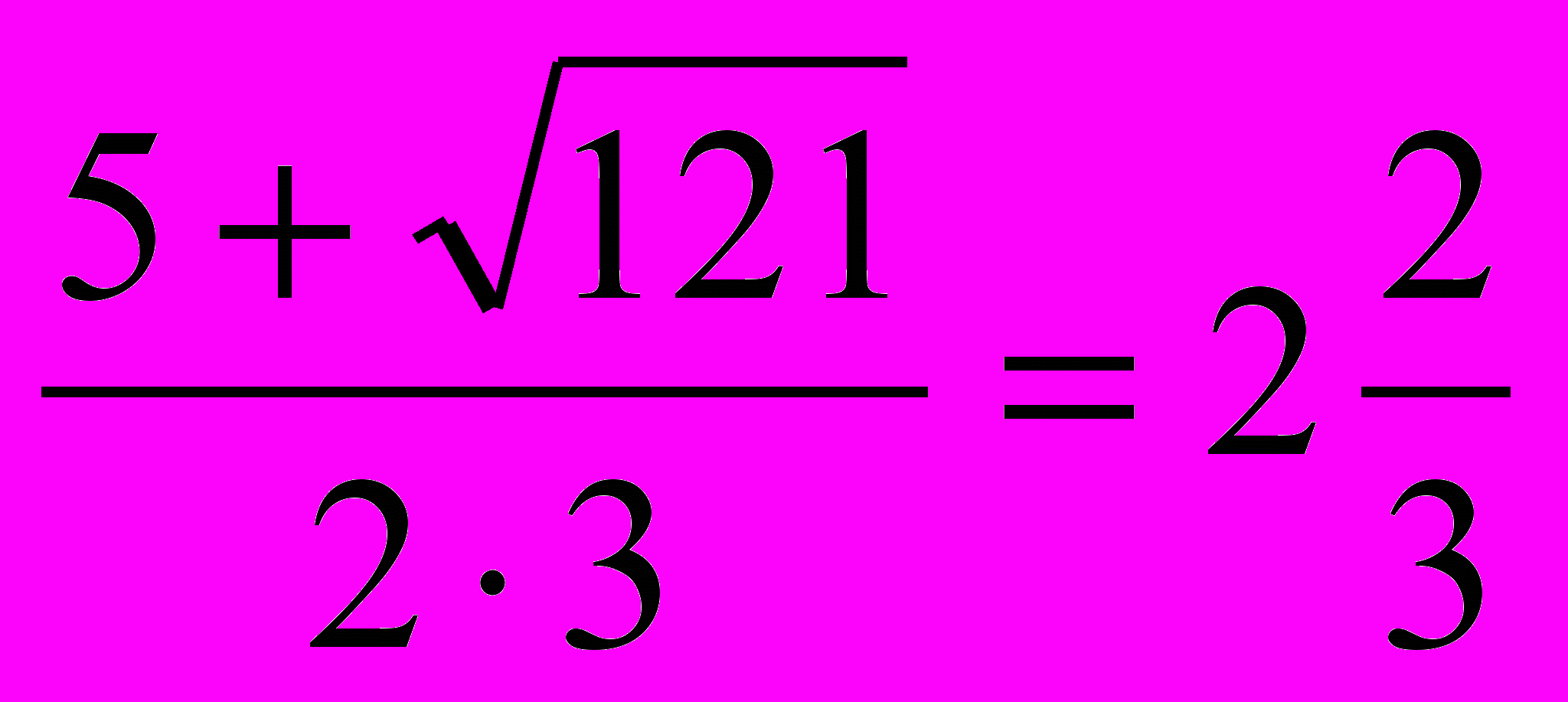
х₂=

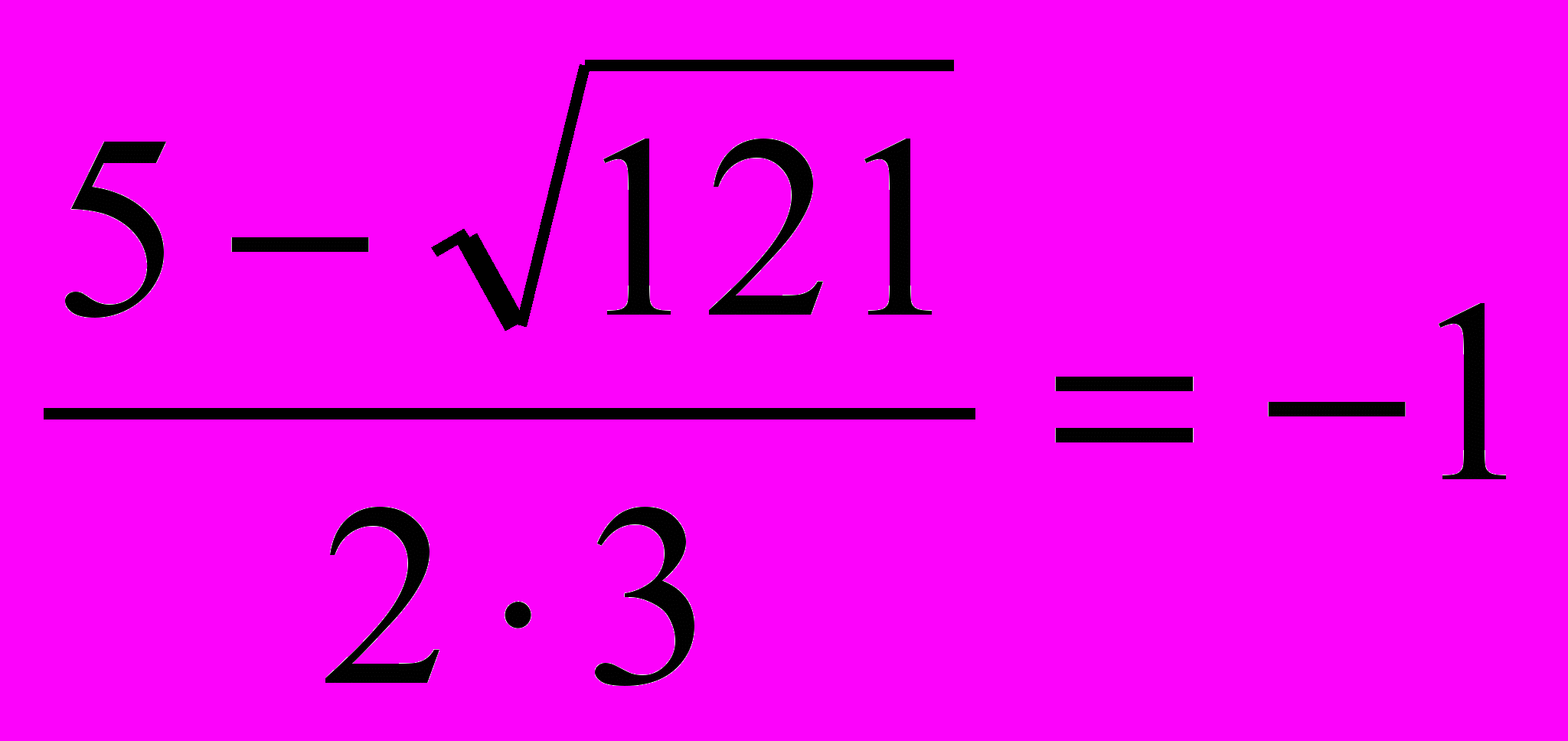
Ответ: .


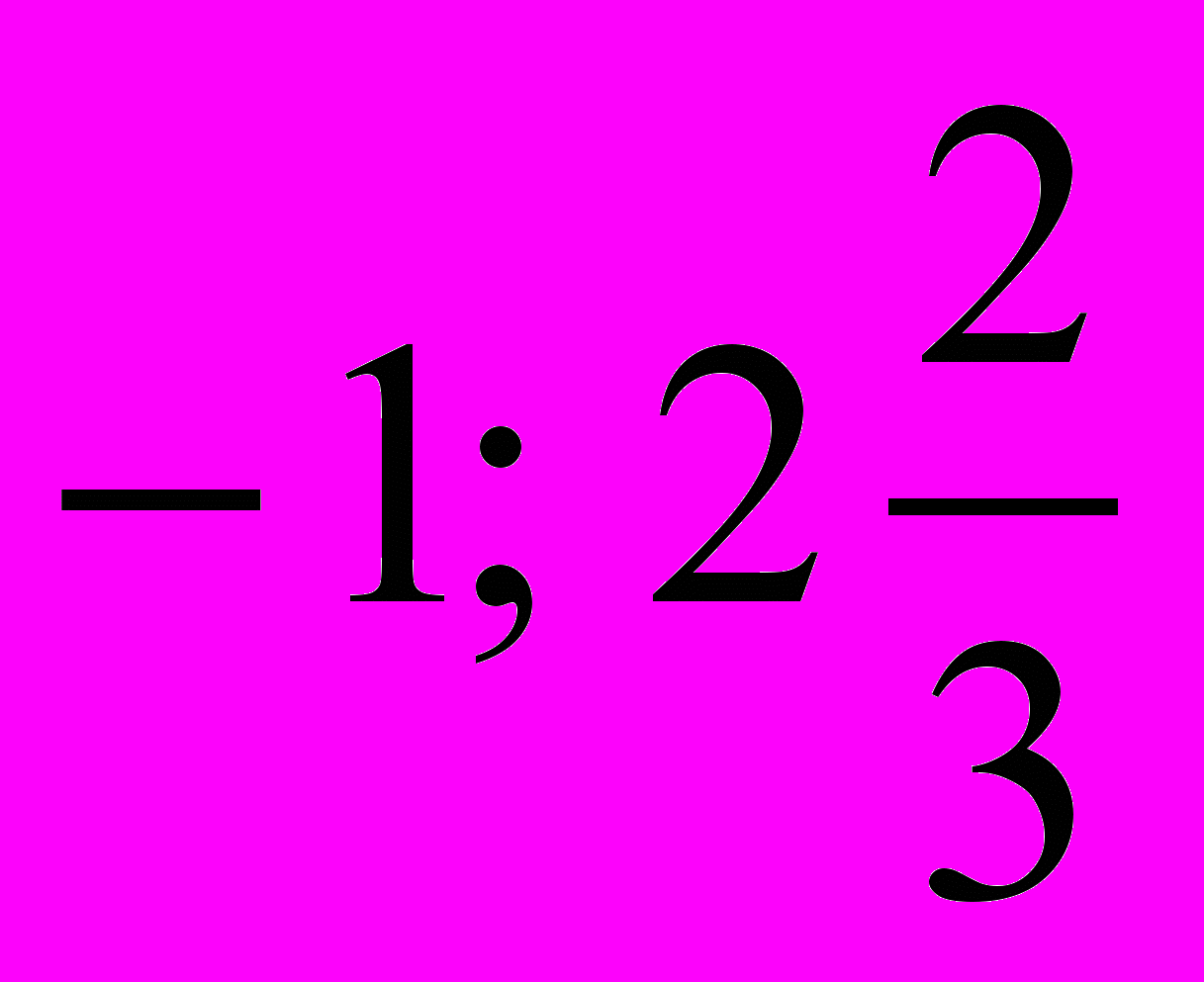в) (х²+1)²–15=2(х²+1)

Пусть х²+1= t; t² – 15 – 2t =0

D=b² – 4ac ; D= (-2)² – 4^.1^.(-15)=64

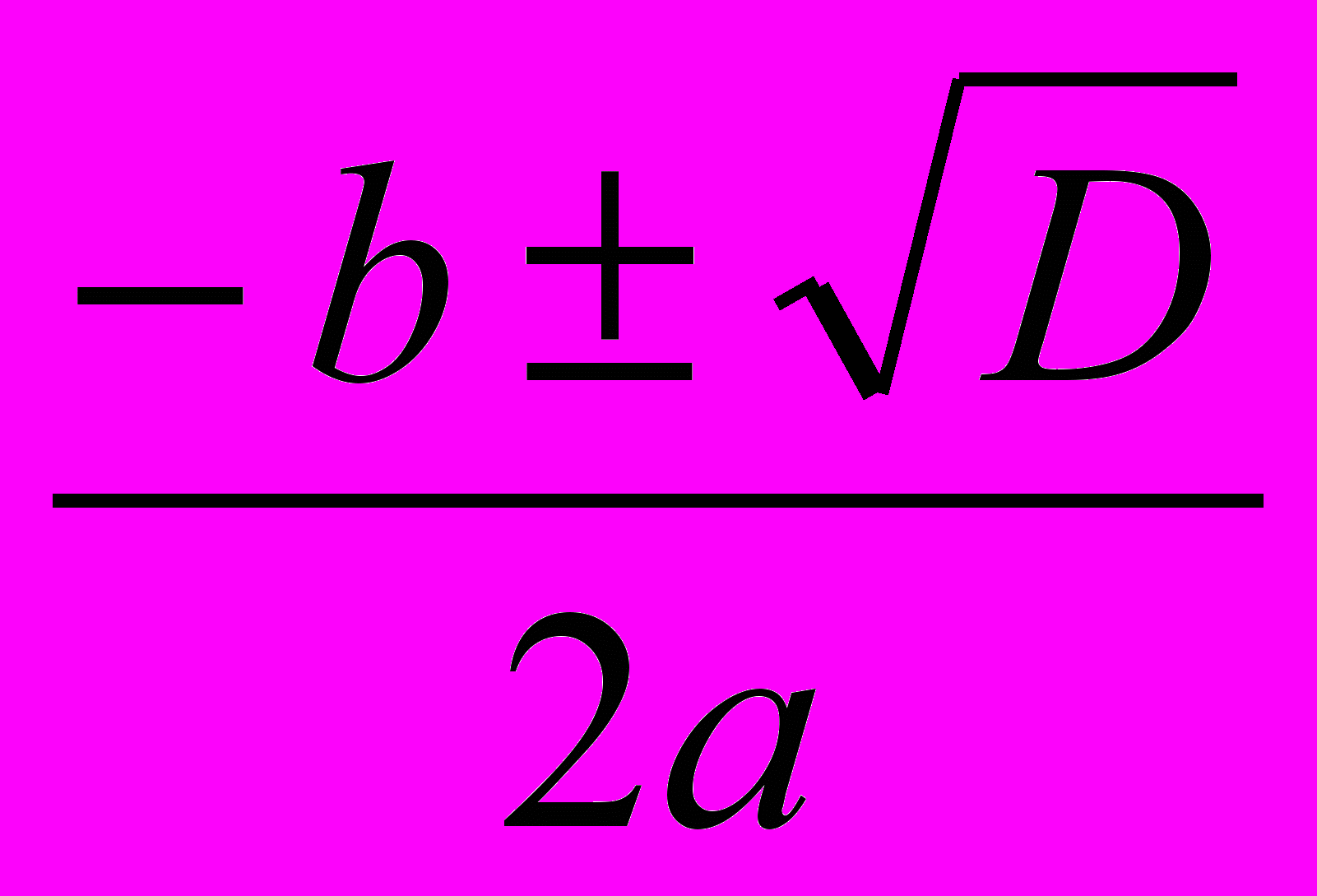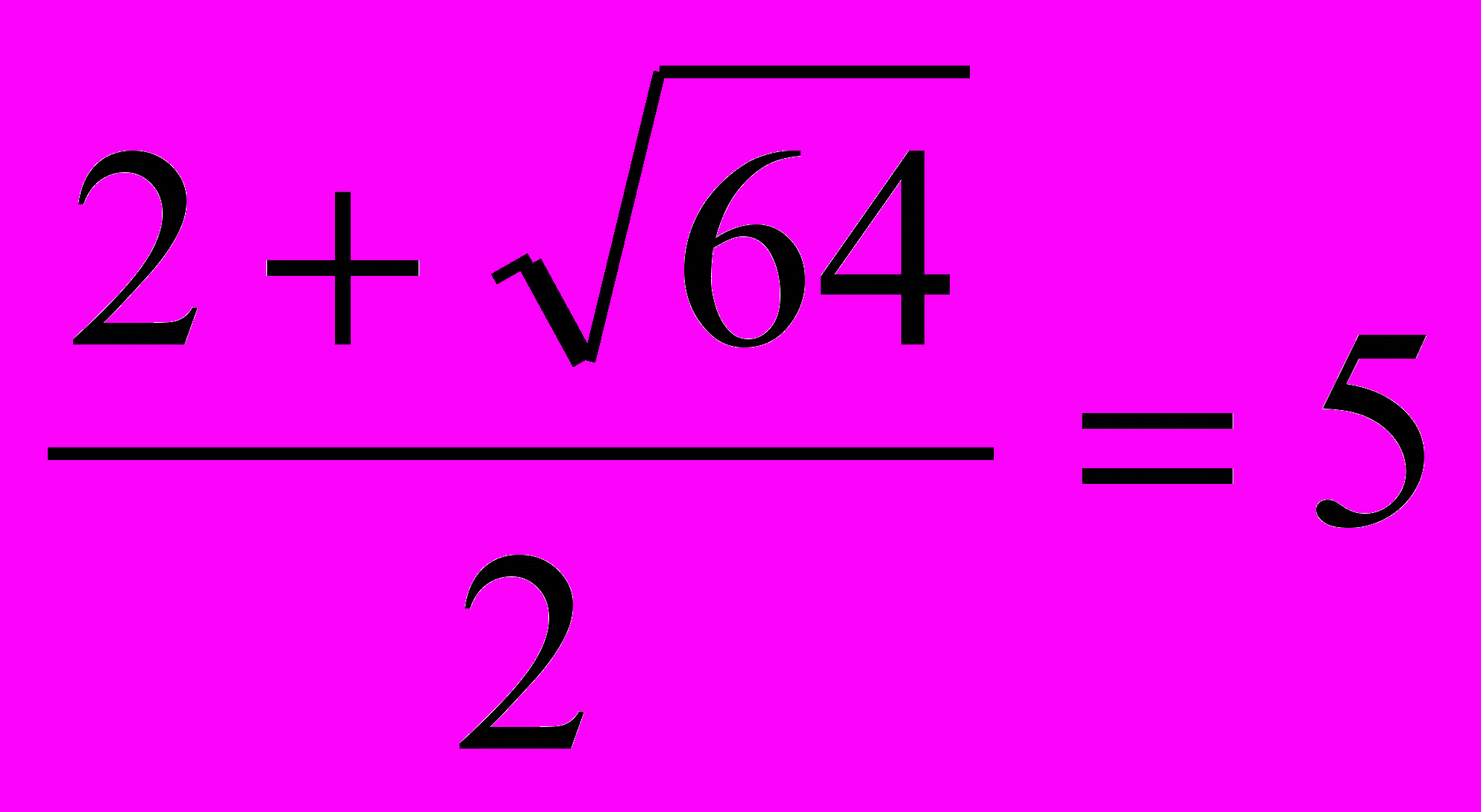t_1,2= ; t₁=; t₂=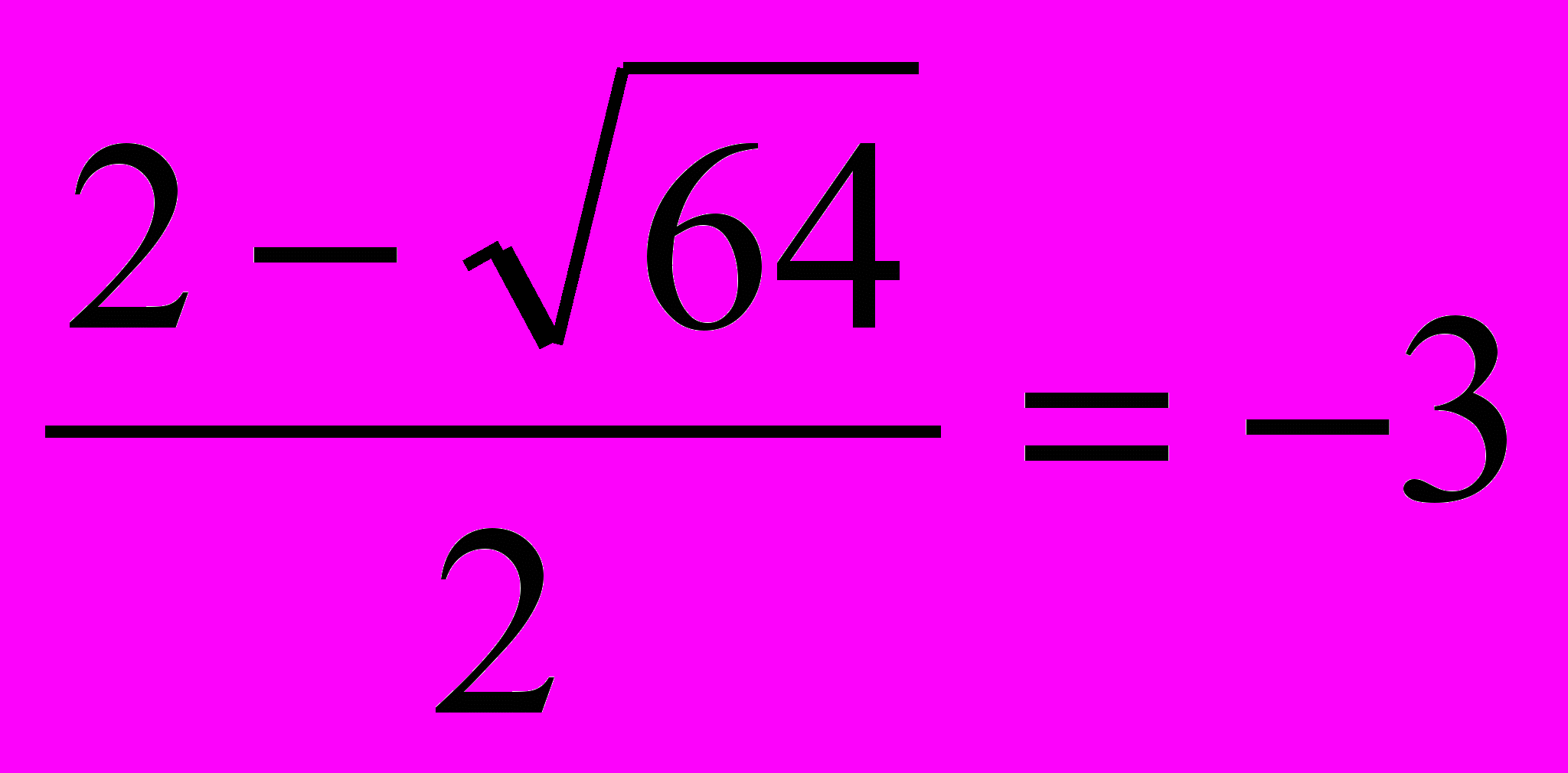 (можно по формуле корней со вторым четным коэффициентом)

х²+1=5 или х²+1= - 3

х² = 4 х² = - 4

х = 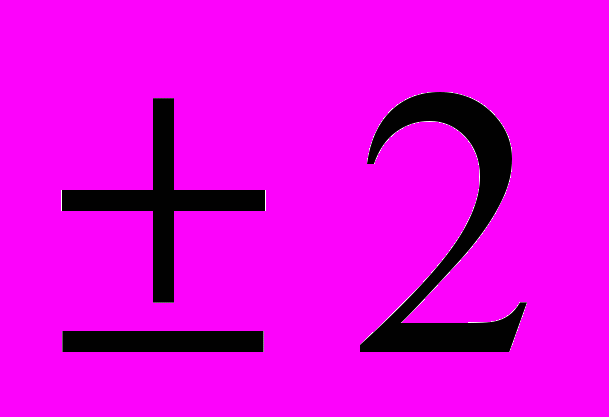корней нет

Ответ: - 2; 2.

4. 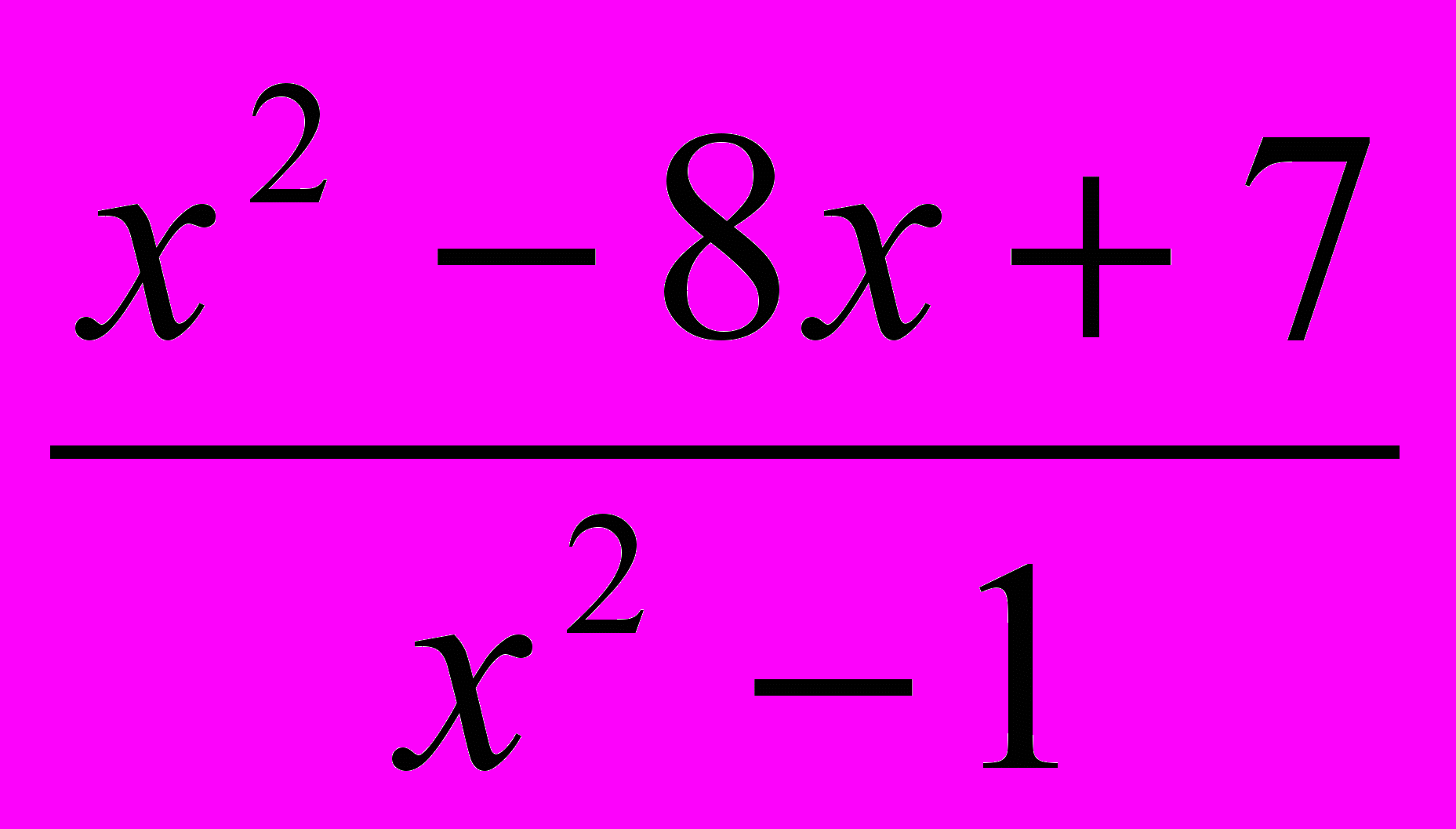= 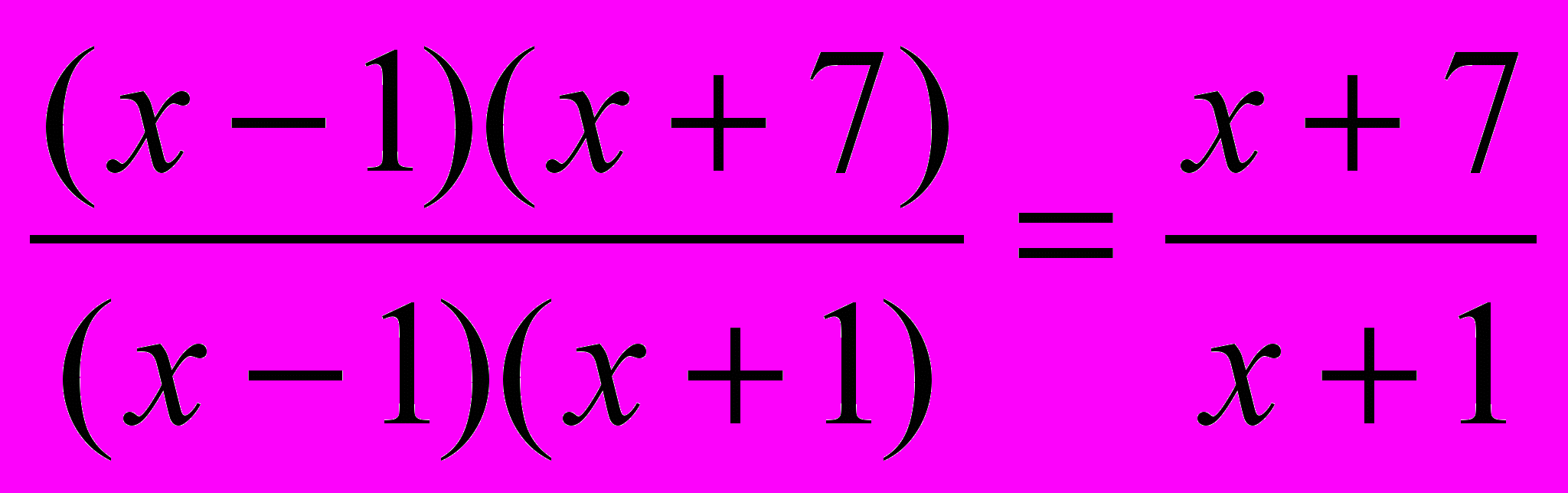Для разложения трехчлена на множители пользуемся решением 3(а).


5. х² – kх – 3 =0; х₁ = 3

По теореме Виета х₁^.х₂= - 3 х₂ = - 1;

x₁+х₂ = - k - k = 2; k = - 2.


6. Пусть х (см) – меньшая сторона прямоугольника.

Тогда 16 – х (см) – большая сторона прямоугольника,

х(16 – х) (см²) – площадь прямоугольника, а по условию площадь 60 см², составим уравнение.

х(16 – х)=60

- х² + 16х – 60 = 0 х² – 16х + 60 = 0

х₁ = 10; х₂ = 6

Ответ: 6 см – меньшая сторона прямоугольника.

Задание 1	Задание 2	Задание 3	Задание 4	Задание 5	Задание 6
а) D<0 , два корня. б) D=0, один корень	а) 0; - 2. б) 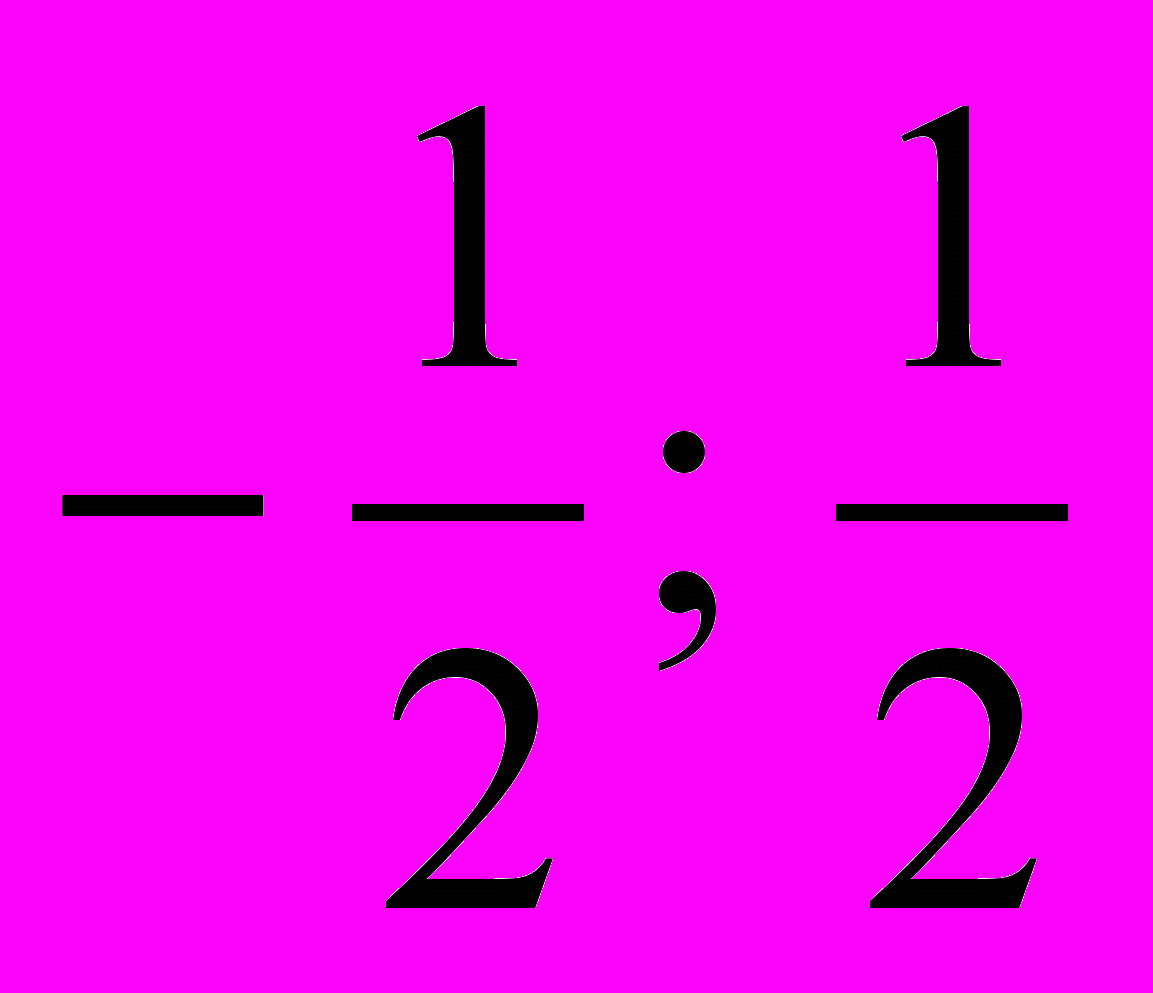. в) 5.	а) - 1; 7 б) 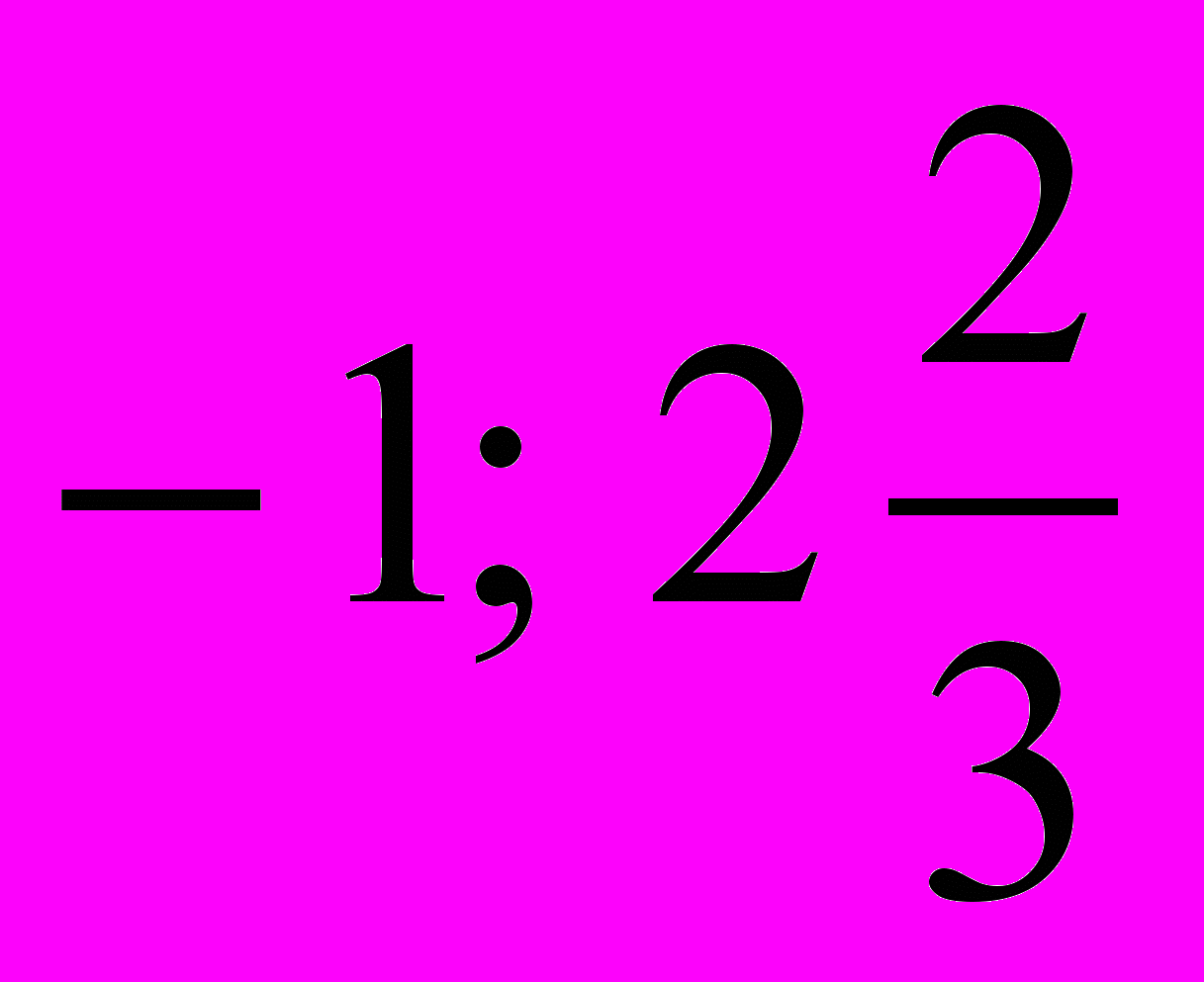в) - 2; 2		х2 = - 1; k = - 2	6 см

2 вариант

Задание 1	Задание 2	Задание 3	Задание 4	Задание 5	Задание 6
а) D > 0, два корня. б) D<0, корней нет	а) б) 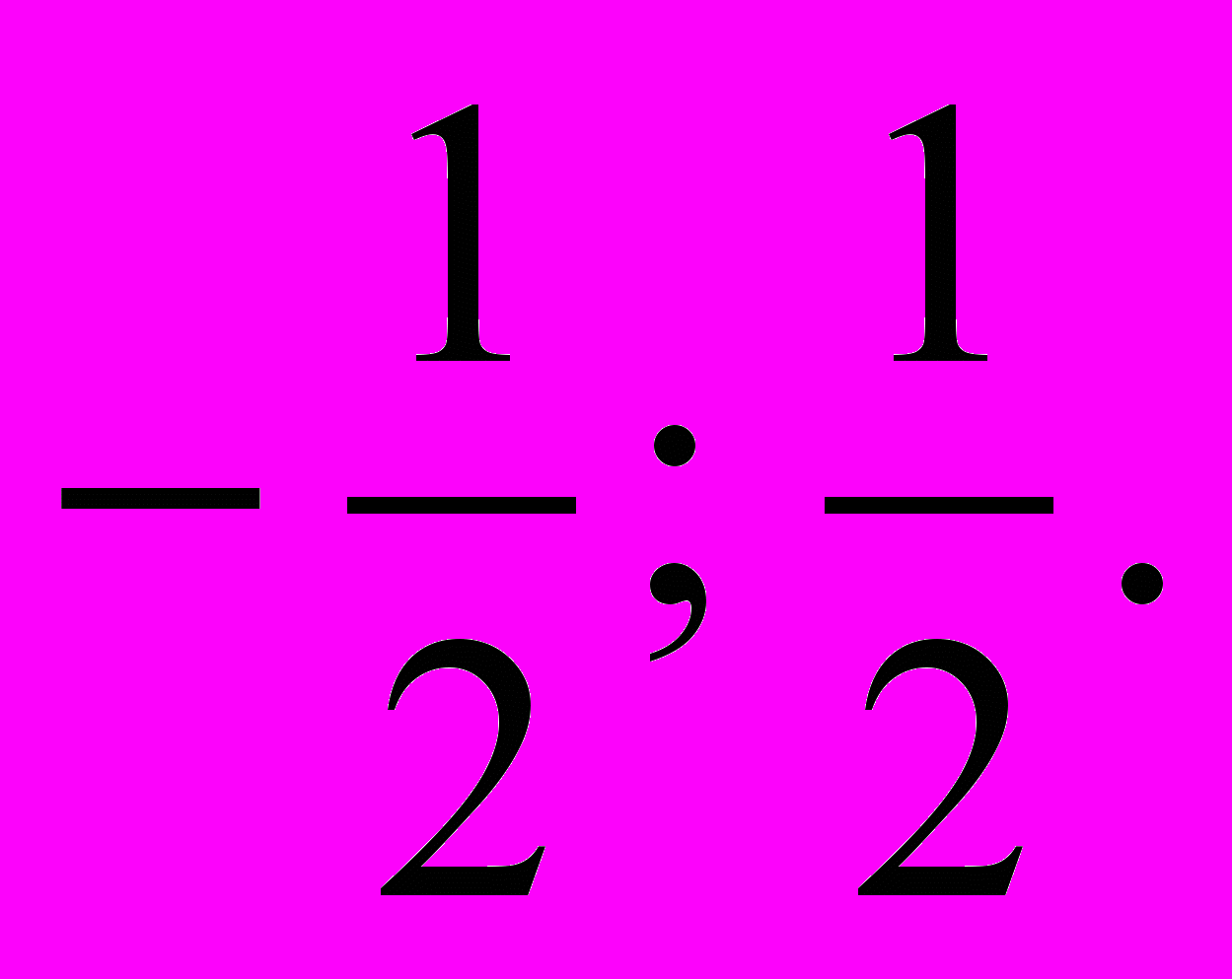в) – 3;	а) – 1; 5. б) . в) – 3; 3.		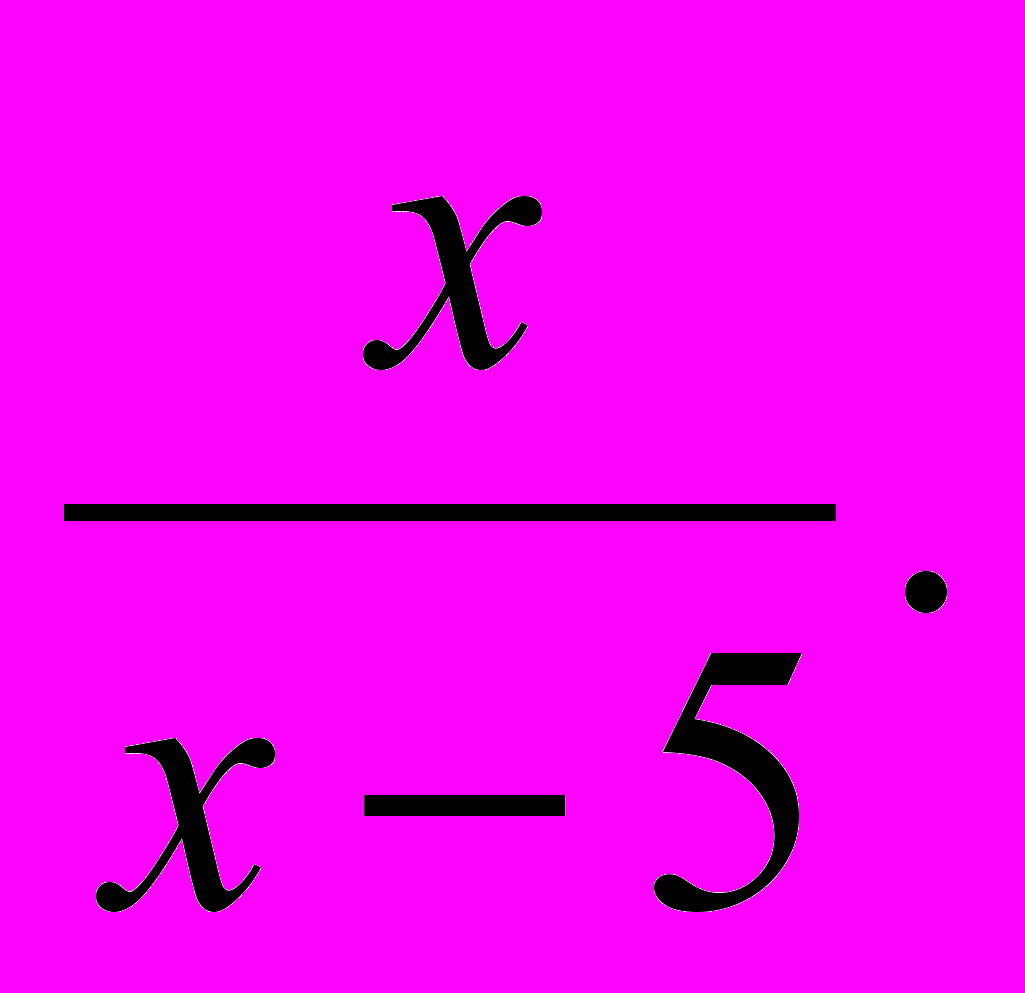х = – 4 ; k = 24.	8 см

Приложение