"Основы финансовой математики" 24

Вид материала

Содержание

Тест для проверки усвоения пройденного материала по теме основные категории финансово-экономических расчетов
2. Финансово-экономические расчеты используются для
3. Подход, при котором фактор времени играет решающую роль, называется
4. Проценты в финансовых расчетах
5. Процентные деньги - это
6. Процентная ставка
7. В качестве единицы времени в финансовых расчетах принят
9. Коэффициент наращения
10. Дисконтирование- это
11. Дисконтный множитель (d)
Тест для проверки усвоения пройденного материала по теме просты проценты
Формула простых процентов
Точный процент – это
Точное число дней финансовой операции можно определить
Французская практика начисления процентов
Германская практика начисления процентов
Английская практика
Расчет наращенной суммы в случае дискретно изменяющейся во времени процентной ставки по схеме сложных процентов имеет следующий
1. Формула сложных процентов
3. Чем больше периодов начисления процентов
...
Полное содержание

Подобный материал:

1 2 3 4 5 6 7

Приложения

Приложение 1

Тест для проверки усвоения пройденного материала по теме основные категории финансово-экономических расчетов

1. Принцип неравноценности денег заключается в том, что:

А - деньги обесцениваются со временем;

В - деньги приносят доход;

С - равные по абсолютной величине денежные суммы, относящиеся к различным моментам времени, оцениваются по-разному;

D - "сегодняшние деньги ценнее завтрашних денег".

2. Финансово-экономические расчеты используются для:

А - определения выручки от реализации продукции;

В - расчета кредитных операций;

С - расчета рентабельности производства;

D - расчета доходности ценных бумаг.

3. Подход, при котором фактор времени играет решающую роль, называется:

А - временной;

В - статический;

С - динамический;

D - статистический.

4. Проценты в финансовых расчетах:

А - это доходность, выраженная в виде десятичной дроби;

В - это абсолютная величина дохода от предоставления денег в долг в любой его форме;

С - показывают, сколько денежных единиц должен заплатить заемщик за пользование в течение определенного периода времени 100 единиц первоначальной суммы долга;

D - это %.

5. Процентные деньги - это:

А - отношение суммы, полученной в результате финансовой операции, к сумме, затраченной на ее проведение;

В - разность между суммой, полученной в результате выполнения финансовой операции и суммой, затраченной на ее проведение;

С - разность между суммой, затраченной на проведение финансовой операции и суммой, полученной в результате ее проведения;

D - относительный показатель, характеризующий доходность финансовой операции.

6. Процентная ставка - это:

А - относительный показатель, характеризующий интенсивность начисления процентов;

В - абсолютная величина дохода от предоставления денег в долг в любой его форме;

С - ставка, зафиксированная в виде определенного числа в финансовых контрактах;

D - отношение суммы процентных денег к величине ссуды.

7. В качестве единицы времени в финансовых расчетах принят:

А – год;

В – квартал;

С - месяц;

D - день.

8. Наращение - это:

А - процесс увеличения капитала за счет присоединения процентов;

В - базисный темп роста;

С - отношение наращенной суммы к первоначальной сумме долга;

D - движение денежного потока от настоящего к будущему.

9. Коэффициент наращения - это:

А - отношение суммы процентных денег к величине первоначальной суммы;

В - отношение наращенной суммы к первоначальной сумме;

С - отношение первоначальной суммы к будущей величине денежной суммы;

D - отношение процентов к процентной ставке.

10. Дисконтирование- это:

А - приведение будущих денег к текущему моменту времени;

В - характеризует долю первоначальной суммы долга в величине наращенной суммы;

С - отношение суммы, наращенной в результате финансовой операции, к сумме, затраченной на ее проведение;

D - отношение суммы, затраченной на проведение финансовой операции, к сумме, полученной в результате ее выполнения.

11. Дисконтный множитель (d) -

А - показывает, какую долю составляет первоначальная сумма долга в величине наращенной суммы;

В - отношение наращенной суммы к первоначальной сумме:

С - отношение наращенной суммы к сумме, полученной в результате выполнения финансовой операции;

D - характеризует зависимость величины процентных денег от длительности (периода) финансовой операции.

Приложение 2.

Тест для проверки усвоения пройденного материала по теме просты проценты

Наращение – это:

А - процесс увеличения капитала за счет присоединения процентов:

В - базисный темп роста:

С - отношение наращенной суммы к первоначальной сумме долга;

D – движение денежного потока от настоящего к будущему

Формула простых процентов:

A - FV = PV*r*n

B - FV = PV*( 1+r)ⁿ

C - FV = PV*(1+n*r)

D - FV = PV*(1+r)

Простые проценты используются в случаях:

А - реинвестирования процентов;

В – выплаты процентов по мере их начисления;

С - краткосрочных ссуд, с однократным начислением процентов;

D – ссуд, с длительностью менее одного года

Точный процент – это:

А - капитализация процента;

В - коммерческий процент;

С - расчет процентов, исходя из продолжительности года в 365 или 366 дней;

D – расчет процентов с точным числом дней финансовой операции

Точное число дней финансовой операции можно определить:

А - по специальным таблицам порядковых номеров дней года:

В – используя прямой счет фактических дней между датами;

С – исходя из продолжительности каждого целого месяца в 30 дней;

D - считая дату выдачи и дату погашения ссуды за один день.

Французская практика начисления процентов:

А - обыкновенный процент с приближенным числом дней финансовой операции:

В - обыкновенный процент с точным числом дней финансовой операции;

С - точный процент с точным числом дней финансовой операции;

D - точный процент с приближенным чистом дней финансовой операции.

Германская практика начисления процентов:

Английская практика:

Расчет наращенной суммы в случае дискретно изменяющейся во времени процентной ставки по схеме сложных процентов имеет следующий вид:

А -

В -

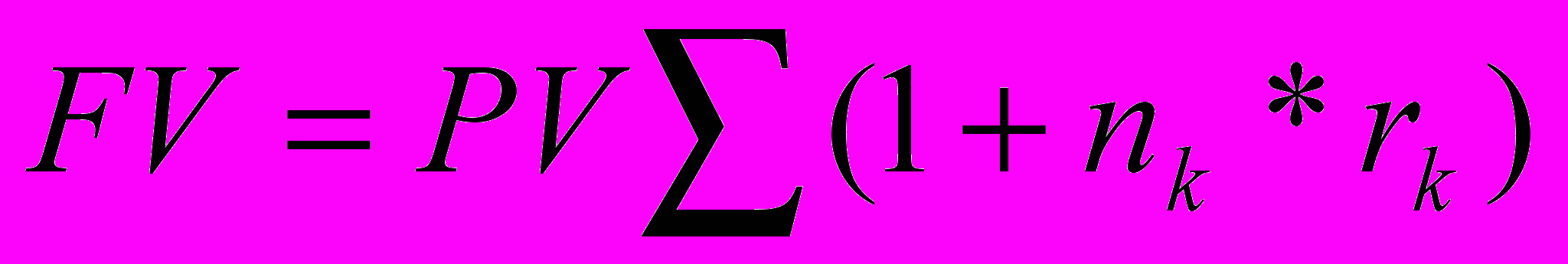
С -

D -

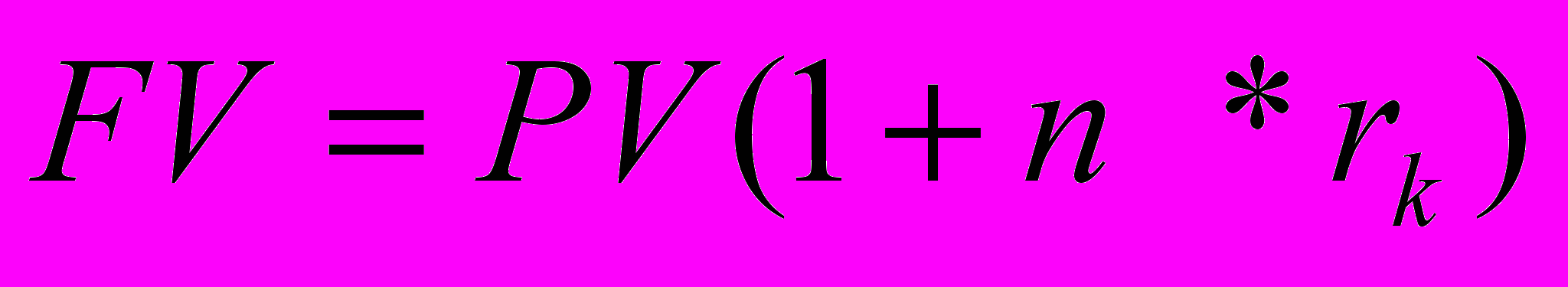
Срок финансовой операции по схеме простых процентов определяется по формуле:

А -

В -

С -

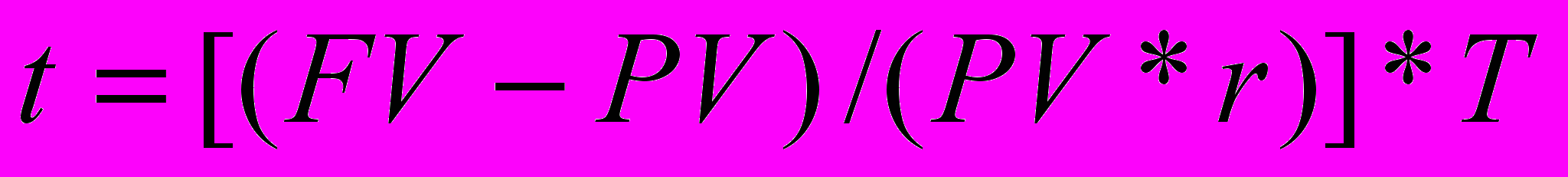
D -

Если в условиях финансовой операции отсутствует простая процентная ставка, то:

А – этого не может быть;

В – ее можно определить по формуле

С – ее невозможно определить

D – ее можно определить по формуле

процентных чисел / дивизор

Приложение 3

Тест для проверки усвоения пройденного материала по теме сложные проценты

1. Формула сложных процентов:

A -FV = PV(1+n*r);

B -FV = PV(1+t / T*r;)

C -FV = PV(1+r)ⁿ;

D -FV = PV(1+n*r)*(1+r)ⁿ;

2. Начисление по схеме сложных процентов предпочтительнее:

А - при краткосрочных финансовых операциях;

В - при сроке финансовой операции в один год;

С - при долгосрочных финансовых операциях;

D - во всех вышеперечисленных случаях.

3. Чем больше периодов начисления процентов:
А - тем медленнее идет процесс наращения;

В - тем быстрее идет процесс наращения;

С - процесс наращения не изменяется;

D - процесс наращения предсказать нельзя.

4. Номинальная ставка - это:

А - годовая ставка процентов, исходя из которой определяется величина ставки процентов в каждом периоде начисления, при начислении сложных процентов несколько раз в год;

В - отношение суммы процентов, выплачиваемых за фиксированный отрезок времени, к величине ссуды;

С - процентная ставка, применяется для декурсивных процентов;

D - годовая ставка, с указанием периода начисления процентов.

5. Формула сложных процентов с неоднократным начислением процентов в течение года:

A - FV = PV(1 +r)^m*ⁿ;

В - FV = PV(1 +r/ т)^т*ⁿ;

C-FV = PV/m *(1+r)^n/^т;

D-FV = PV(1+r*m)^m*ⁿ.

6 Эффективная ставка процентов:

А - не отражает эффективности финансовой операции:

В - измеряет реальный относительный доход;

С - отражает эффект финансовой операции:

D - зависит от количества начислении и величины первоначальной cуммы.

7. Формула сложных процентов с использованием переменных
процентных ставок:

A - FV = PV(1 +r₁)ⁿ¹*(1+r₂)ⁿ²*…*(1+r_k)^nk;

В - FV = PV(1 +n_kr_k);

C-FV = PV*(1+n₁r₁*n₂r₂*…*n_kr_k)^nk;

D-FV = PV(1+r*n)*(1+r).

8. В случае, когда срок финансовой операции выражен дробным числом лет, начисление процентов возможно с использованием:

А - общего метода;

В - эффективной процентной ставки;

С - смешанного метода;

D - переменных процентных ставок.

9. Смешанный метод расчета:

A -FV = PV(1+r)^a ⁺ ^b;

B - FV = PV(1+r)^a*(1+br);

C - FV = PV(1 +a*b*r)ⁿ;

D - FV = PV(1 + r)^a *(1 + r)^b.

10. Непрерывное начисление процентов - это:
А - начисление процентов ежедневно;

В - начисление процентов ежечасно;

С - начисление процентов ежеминутно;

D - начисление процентов за нефиксированный промежуток времени.

Приложение 4.

Список задач для самостоятельного решения на простые проценты

Задание 1-1

Ссуда в размере 50000 руб. выдана на полгода по простой ставке 28% годовых. Определить наращенную сумму и сумму начисленных процентов.

Ответ: FV= 57000: 1= 7000 (руб.) Задание 12

Задание 1-2

Ссуда в размере 1 млн. руб. выдана 20.01.06 до 05.10.06 под 18% годовых. Определить сумму начисленных процентов.

Ответ:

Английская схема-127232,88 (руб.);

Германская схема- 127500 (руб.);

Французская схема - 129000 (руб.)

Задание 1-3

Кредит в размере 200000 руб. выдается на 3,5 года. Ставка процентов за первый год - 30%. а за каждое последующее полугодие она уменьшается на 1%. Определить множитель наращения и наращенную сумму.

Ответ: k_n= 1.83; FV = 165000

Задание 1-4

Ссуда выдана под 10% годовых сроком: а) на 5 месяцев; б) на 3 месяца. Определить процентную ставку за срок ссуды

Ответ: а)г=0, 0417: б) 1 = 0,025

Задание 1-5

Определить проценты, множитель наращения и сумму накопленного долга, если ссуда равна 100 тыс. руб., срок долга - 2 месяца, номинальная процентная ставка - 10%.

Ответ: PV= 101667 руб.

Задание 1-6

Вклад в 500 тыс. руб. был размещен в банке 11.06.2006 г. По ставке 80% годовых. При востребовании вклада 20.09.2006 г. вкладчику были начислены проценты в размере 110 тыс. руб. определите, какую практику начисления процентов использовал банк.

Ответ: Использовалась германская практика начисления процентов

Задание 1-7

Банк принимает вклады до востребования по ставке 10% годовых. Определите накопленную сумму и сумму начисленных процентов при английской практике их начисления для вклада 500 тыс. руб., размешенного на срок с 5.01.2006 г. по 25.10.2006 г.

Ответ: FV=540136.99 руб.; I = 40136.99руб.

Задание 1-8

Определить процентную ставку, которую использует банк для вкладов до востребования, если при первоначальной сумме вклада 1000 руб. через 6 месяцев начислено 1084 руб.

Ответ: r = 16.8%

Задание 1-9

Договор предусматривает следующие ставки простых процентов:
за I квартал - 230% годовых.

за 2-ой и третий - 240% годовых,

за четвертый - 200% годовых.

Определить множитель наращения за год.

Ответ: k_п =4.55

Задание 1-10

Вкладчик собирается положить в банк 500 тыс. руб.. чтобы накопить 700 тыс.руб. Ставка процентов банка составляет 60% годовых. Определите срок в днях, за который вкладчик сможет накопить требуемую сумму (число дней в году равно 360).

Ответ: t = 240 дней

Задание 1-11

Вкладчик, решивший положить на депозит 250 тыс. руб.. хочет накопить через год не менее 400 тыс. руб. Определить ставку процентов, на основании которой он может выбрать подходящий для этой цели банк.

Ответ: r =60%

Приложение 5

Список задач для самостоятельного решения на сложные проценты

Задача 1-12

Ссуда в размере 50000 руб. выдана на полгода по сложной ставке 18% годовых. Определить наращенную сумму и сумму начисленных процентов. Ответ: FV= 57000: I=7000 (руб.)

Задание 1-13

Рассчитать какая сумма окажется на счете, если 27 тыс. руб. положены на 33 года под 13.5% годовых. Проценты начисляются каждые полгода.

Ответ: 2 012 074.64р

Задание 1-14

По вкладу в 10000,00 помещенному в банк под 5% годовых, начисляемых ежегодно была выплачена сумма 12762,82.

а) Определить срок проведения операции (количество периодов начисления).

б) используя построение сценария (или таблицу подстановки), выясните, как влияет банковский процент (в диапазоне от 1% до 10%) на срок получения указанной суммы.
Постройте диаграмму, отражающую эту
зависимость.

Ответ: а) 5 лет

Задание 1-15

Сумма в 10000 помешена в банк на депозит сроком на 4 года. Ставка по депозиту - 10% годовых. Проценты по депозиту начисляются раз в год.

а) Какова будет величина депозита в конце срока?

б) На какой срок должны быть положены деньги на депозит, с тем, чтобы к

концу срока накопленная сумма составила 20000руб.

в) Постройте диаграмму иллюстрирующую зависимость величины

наращенной суммы от периода времени наращения

Ответ:

а) 14 641.00р.

б) 7.27 года

Задание 1-16

Был сделан заем в 1000 тыс. руб. с номинальной процентной ставкой 12% и сроком уплаты 3 года. Какая сумма будет выплачена кредитору в конце срока, если начисление процентов: полугодовое, квартальное, ежемесячное, ежедневное.

Ответ:

а) 1418.53; b) 1425.76: с) 1430.77: d) 1433.24

Задание 1-17

Вкладчик, решивший положить на депозит 250 тыс. руб., хочет накопить через год не менее 400 тыс. руб. Определить ставку процентов, на основании которой он может выбрать подходящий для этой цели банк. Начисление процентов банков производится непрерывно.

Ответ: r =47%

Задание 1-18

Определить процентную ставку, которую использует банк для вкладов до востребования, если при первоначальной сумме вклада 1000 руб. через 6 месяцев начислено 1084 руб.

Ответ: г = 16,24%

Задание 1-19

Вкладчик собирается положить в банк 500 тыс. руб., чтобы накопить 700 тыс. руб. Ставка процентов банка составляет 15% годовых. Проценты начисляются ежемесячно.

Определите срок в днях, за который вкладчик сможет накопить требуемую сумму (число дней в году равно 360).

Ответ: t = 2.26 года = 812.56дн.

Приложение 6

Список задач для самостоятельного решения по теме дисконтирование

Задание 1-20

Через 250 дней с момента подписания контракта необходимо уплатить 500 тыс. руб., исходя из 10% годовых и временной базы 360 дней. Определить первоначальную сумму долга.

Ответ FV =467532.47

Задание 1-21

Вексель выдан на 5000 руб. с уплатой 17 ноября, а владелец учел его в банке 19 августа того же года по учетной ставке 8%. Определить сумму, полученную предъявителем векселя и доход банка при реализации дисконта.

Ответ: РV = 4900 D = 100

Задание 1-22

Вексель на сумму 100 тыс. руб. и сроком платежа через 3 года продан с дисконтом по сложной учетной ставке 30% годовых. Какова сумма дисконта и современная величина платежа?
Ответ: D = 65700.00 PV = 34300.00

Задание 1-23

Определить величину суммы, выдаваемую заемщику, если он обязуется вернуть ее через два года в размере 55 тыс. руб. Банк определяет свой доход с использованием годовой учетной ставки 30%.

Ответ: PV = 26950.00

Задание 1-24

Вексель на сумму 10 тыс.руб. со сроком погашения 15.11.07г. предъявлен в банк для оплаты 15.08.06г. Банк учел вексель по сложной учетной ставке 30% годовых. Определите сумму, выплаченную владельцу векселя, и сумму дисконта банка при германской практике расчетов.

Ответ: PV = 6402.84

Задание 1-25

При закупке партии товара торговец подписал вексель, обязуясь заплатить 240 тыс. руб. через 150 дней. Поставщик сразу же продал вексель банку при норме дисконта 10%. Какую сумму получил поставщик?.

Ответ: PV = 230000.00

Приложение 7.

План конспект одного урока

Урок 4-5

Тема: Определение срока ссуды и величины процентной ставки

Тип урока: комбинированный урок, урок решения задач

Цели:

РЦ: Способствовать развитию умений анализировать, систематизировать, обобщать, составлять план, делать выводы. Формировать умения и навыки применения процентов для количественной характеристики различных явлений окружающего мира.

ВЦ: Через организацию урока воспитывать активность в учебной работе и самостоятельность.

ОЦ: Углубление и расширение знаний по теме простые проценты. Обеспечение отработки умений. Обучить решению типовых задач на проценты с применением формул простых процентов.

Оборудование: интерактивная доска с записью плана занятия.

План урока:

Актуализация опорных знаний
Определить формулу срока и величины процентной ставки
Решение задач на нахождение срока и величины процентной ставки
Проверка знаний пройденного материала по теме простые проценты в виде тестирования
Самостоятельное решение задач (парная работа)

Запись плана занятия позволит учащимся настроиться на определенный объем работы.

Ход урока

I. В организационной части учитель дает информацию о значимости темы, об объеме изучаемого материала, записывает тему и план урока на доске, дает установку на обязательную запись читаемого в тетрадях.

II. Актуализация необходимых знаний в форме устного мини-опроса по следующей системе вопросов:

Какие четыре величины присутствуют в любой простейшей финансовой операции ? Напишите на доске их символьное обозначение (время = n; текущая стоимость = PV; будущая стоимость = FV; процентная ставка = r)
Назовите формулу для наращения вложенной суммы по схеме простых процентов ( FV=PV*(1+r*n) )
Назовите формулу для наращения вложенной суммы, если процентная ставка r изменяется во времени ()

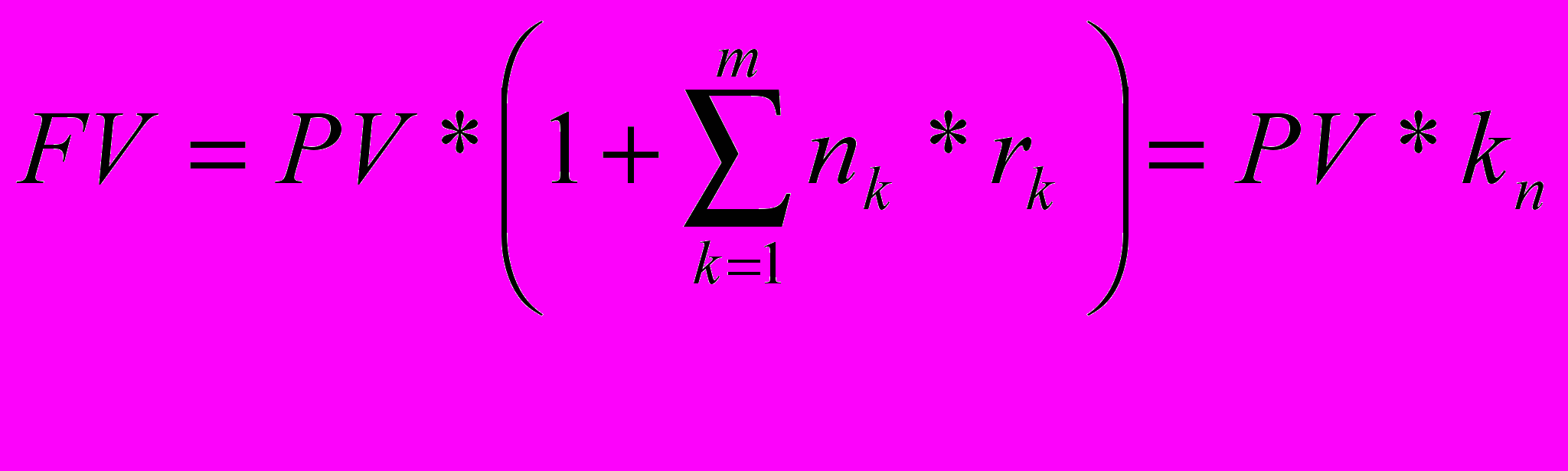Комментарий: Актуализация знаний в форме перечисленных выше вопросов способствует осмысленному восприятию теории простых процентов.

I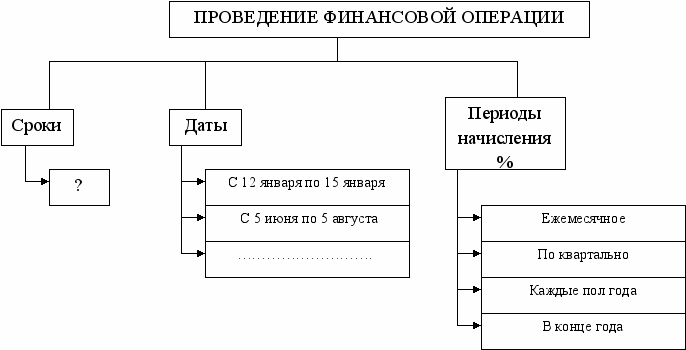II. Введение новых формул начинается с информационного сообщения учителя с использованием блок схемы.

“Как правило, при проведении финансовых операций обязательно фиксируются сроки, даты, периоды начисления процентов, так как фактор времени (как мы уже отмечали) в финансово-коммерческих расчетах играет важную роль...

Однако достаточно часто возникают ситуации, когда срок финансовой операции в условиях конкретной финансовой сделки не может быть оговорен заранее, а когда определяется при достижении какой-то цели финансовой операции (конечной или промежуточной)….

Подобным же образом может обстоять дело и с определением величины процентной ставки. Так, например, на начальном этапе заключения коммерческой сделки нас могут интересовать только величины вложенных (PV) и полученных сумм (FV). В тоже время при анализе эффективности этой сделки возникает вопрос степени ее доходности”…

Эти величины могут быть легко определены из введенных ранее формул определения наращения вложенной суммы по схеме простых процентов.

Срок финансовой операции может быть определен как:

при определении срока в годах - n=(FV-PV)/(PV*r)…………..(1)

при определении срока в днях - t=[(FV-PV)/(PV*r)]*T………(2)

Процентная ставка может быть определена как:

r=(FV-PV)/(PV*n)=[(FV-PV)/(PV*t)]*T………(3)

Комментарий: Сопоставление формул процентной ставки и сроков по годам и дням помогает осознать сущность вводимой информации.

VI. Отработка новых знаний осуществляется через решение 3-х задач по трем введенным формулам. Учитель последовательно представляет текст задачи на интерактивной доске, обсуждает содержание, выявляет совместными усилиями формулу для ее решения и записывает решение.

Задача 1.

За какое время может быть накоплена сумма в 2000 долларов, если сегодня мы можем оформить депозитный вклад 1000 долларов под 10% годовых.

Проведем анализ содержания и поиск плана решения задачи.

Анализ содержания задачи:

О чем идет речь в задаче? (речь идет о вкладчике, который положил деньги в банк под 10% годовых)
Какие величины известны? (текущая стоимость PV=1000; будущая стоимость FV=2000; процентная ставка r=10%)
Что необходимо найти? (срок накопления капитала (n) в размере 2000 )
Какой формулой связаны величины? (формула 1)
Можно ли сразу решить задачу или нужны дополнительные условия…?

Решение: п = (FV-PV)/(PV *n)= (2ООО-1ООО)/(1ООО*О,1) = 10 лет

Задача 2.

На сколько дней можно дать в долг 1000 долларов, исходя из 8% годовых, если возвращенная сумма должна составлять 1100 долларов.

Проведем анализ содержания и поиск плана решения задачи.

Анализ содержания задачи:

О чем идет речь в задаче? (речь идет о кредиторе, который дал деньги в долг на 1 год под 8% годовых)
Какие величины известны? (текущая стоимость PV=1000; будущая стоимость FV=1100; процентная ставка r=8%)
Что необходимо найти? (срок накопления капитала (n) в размере 1100 )
Отличается ли эта задача от предыдущей и если да то чем? (отличается тем. Что срок финансовой операции определен в днях)
Какой формулой связаны величины? (формула 2)
Можно ли сразу решить задачу или нужны дополнительные условия…?

Решение: t= [(FV-PV)/(PV*r)] *T= (1100-1000)/(1000*0.08)*360 =450 дней

Задача 3.

В контракте предусматривается погашение обязательств через 120 дней в сумме 1200 долларов, при первоначальной сумме долга 1150 долларов. Определить доходность операции для кредитора в виде процентной ставки.

Проведем анализ содержания и поиск плана решения задачи.

Анализ содержания задачи:

О чем идет речь в задаче? (речь идет о кредиторе, который дал деньги в долг на 120 дней)
Какие величины известны? (текущая стоимость PV=1150; будущая стоимость FV=1200; срок n=120 дней)
Что необходимо найти? (процентную ставку r )
Какой формулой связаны величины? (формула 3)
Можно ли сразу решить задачу или нужны дополнительные условия…?

Комментарий: Перед решением необходимо задать следующий уточняющий вопрос: Используя, какую формулу, будем рассчитывать годовую процентную ставку? (Рассчитываем годовую процентную ставку, используя формулу «обыкновенного процента», поскольку в условиях сделки нет ссылки на точный процент)

Решение: r=(FV-PV)/(PV*n)=[(FV-PV)/(PV*t)]*T =[(1200- 1150)/(1150* 120)] * 360 = 0.13

Задача 4. (Решите самостоятельно)

Банк выдал ссуду в размере 100000 рублей сроком:

а) на 5 месяцев: б) на 3 месяца.

Какими должны быть процентные ставки с тем. чтобы доход банка (не зависимо от срока ссуды) составил 120000 рублей?

VI. Итог урока

Что узнали на уроке?

Что позволяют узнать формулы простого процентного роста?

Как называется величина (1+r*n) ?

VI. Д/З

Кредит в размере 15 000 руб. выдан с 26.03 по 18.10 под простые 24% годовых. Определить размеры долга для различных вариантов начисления процентов.
Клиент внес в банк 14 000 д.ед. на срок с 14 февраля по 23 июля. На вклады «до востребования» сроком больше месяца банк начисляет 24 % простых годовых. Определите наращенную сумму при расчете по: а) точным процентам с точным числом дней; б) банковскому методу; в) обыкновенным процентам с приближенным числом дней. Год не високосный.

Blog

"Основы финансовой математики" 24

Содержание

Приложения